代码随想录算法训练营第四十四天 | 01背包问题 二维、 01背包问题 一维、416. 分割等和子集
01背包问题 二维
代码随想录视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
 1.dp数组定义
1.dp数组定义
dp[i][j] 下标为[0,i]之间的物品,任取放容量为j的背包的最大价值
2.递推公式
不放物品i: dp[i-1][j] 去看是否放i-1,还是有j的容量给i-1去放
放物品i : dp[i-1][j-weight[i]] + value[i],放了物品i,那么就只有j-weight[i]的容量给i-1个物品去放了,同时要加上我这个物体的价值
dp[i][j] = max(上面两个),取最大价值
3.数组初始化

首先看,i是由i-1推出来的,j是否左上的某一个格子或者正上推出来的(背包剩余容量)
dp[i][0] = 0,背包的容量为0,不管放哪个,价值都为0
dp[0][j] , 当背包可以装下这个物品开始,dp[0][j]就等于这个物品的价值,装不下就为0
4.遍历顺序
for(i<weight.size() ) 物品
for(j<=bagweight ) 背包
对于二维数组实现的01背包,物品和背包的遍历顺序是可以颠倒的,因为左上方和上方是有值的
循环体内是正序还是倒序都是可以的,因为都是根据上一行的数据来进行推导的
01背包问题 一维
代码随想录视频讲解:带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
因为这里的i层都是由i-1层推到出来的,因此只需要一个一行的一维滚动数组来维护就可以了,不需要整个二维数组
1. dp[j] 容量为j的背包的最大价值为dp[j]
2.递推公式
不放物品i,就是自己dp[j],也就是把上一层数据拷贝下来
放物品i , dp[j-weight[i]] + value[i]
dp[j] = max(上面两个)
3.初始化
dp[0]=0 , 背包容量为0的时候,最大价值为0
非零下标都是初始化为0,因为为其他的话,会覆盖掉递推公式中算出来的值
4.遍历顺序
for(i<weight.size()) 物品
for(j=bagweight,j>=weight[0] ) 背包
采用倒序,是为了防止物品重复选取,比较的数据来自上一轮
正序遍历就是用同一个物品塞满背包,每次覆盖的数据都是同一个物品塞满的情况
dp【i】【j】的更新只与dp【i-1】【j】和dp【i-1】【j-weight_i】左上角这两个数据有关,而与右边的数据无关,那么从右向左遍历,遍历时左边的数据还是上一行的数据没有更新, 这样子用一行数组很好的实现了我们的最终目的
在一维中,只能先遍历物品,再遍历背包
如果先遍历背包,再遍历物品,那记录的就是只有一个物品
416. 分割等和子集
代码随想录视频讲解:动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
解题思路
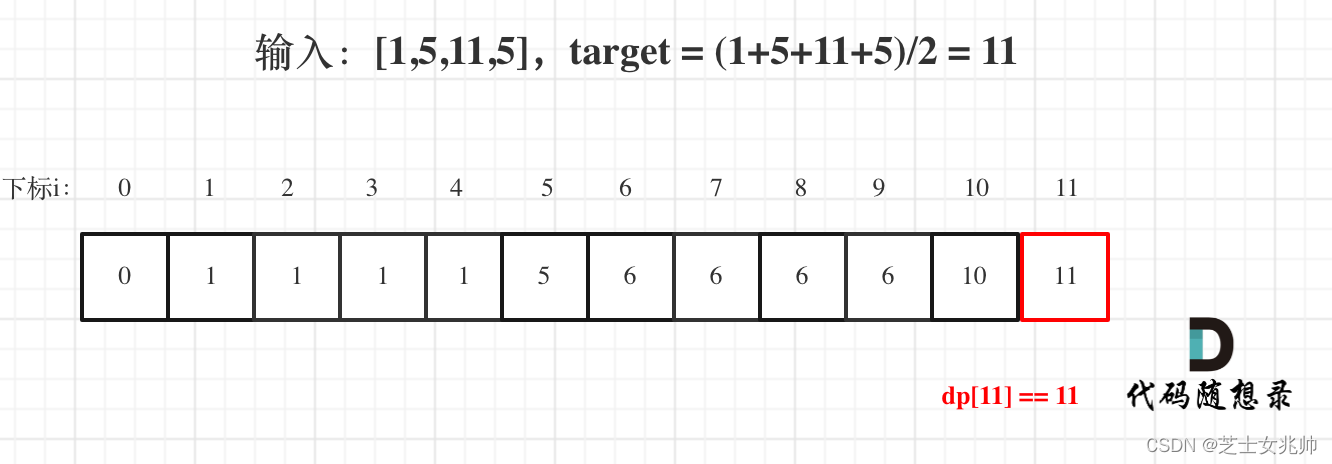
本题元素只能使用1次,并且看能不能装满11这个背包
1.dp[j] 容量为j的背包的最大价值,本题最大价值和重量,都是数字本身
2. dp[j] = max(dp[j], dp[j-nums[i] + nums[i]])
3.dp[0] = 0;非零下标,初始为非负整数的最小值,也就是0,因为是由max得来的
4.遍历顺序,先遍历物品,再遍历背包,背包是倒序,j要大于等于nums[i],且每个物品只能使用一次
最后去判断背包是否装满了 dp[target] == target
class Solution {
public:bool canPartition(vector<int>& nums) {int sum =0;for(int i: nums)sum+=i;if(sum%2!=0) return false;int target = sum/2;vector<int> dp(target+1,0);for(int i=0 ; i< nums.size(); i++) //物品{for(int j = target; j>=nums[i] ; j--) //背包{dp[j] = max(dp[j], dp[j- nums[i] ] + nums[i] ); //这题物品和价值是一样的}}if(dp[target]==target) return true;else return false;}
};收获
今天掌握了01背包的理论基础,本尝试应用
相关文章:

代码随想录算法训练营第四十四天 | 01背包问题 二维、 01背包问题 一维、416. 分割等和子集
01背包问题 二维 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili 1.dp数组定义 dp[i][j] 下标为[0,i]之间的物品&…...

redis常见使用场景
文章目录 redis常见使用场景全局ID位统计购物车用户消息时间线timeline抽奖商品筛选分布式锁限流redis实现计数器排行榜消息队列redis 如何实现延时队列 redis生产常用的场景 redis常见使用场景 Redis 是一种高性能的内存数据库,广泛应用于各种场景中。以下是 Redi…...
算法更新公式推导)
模糊C均值(FCM)算法更新公式推导
模糊C均值(FCM)算法更新公式推导 目标函数 FCM的目标函数为: J m ∑ i 1 n ∑ j 1 k u i j m ∥ x i − c j ∥ 2 J_m \sum_{i1}^n \sum_{j1}^k u_{ij}^m \|x_i - c_j\|^2 Jmi1∑nj1∑kuijm∥xi−cj∥2 其中: …...

金融创新浪潮下的拆分盘投资探索
随着数字化时代的步伐加速,金融领域正经历着前所未有的变革。在众多金融创新中,拆分盘作为一种新兴的投资模式,以其独特的增长机制,吸引了投资者的广泛关注。本文将对拆分盘的投资逻辑进行深入剖析,并结合具体案例&…...

一份不知道哪里来的第十五届国赛模拟题
这是一个不知道来源的模拟题目,没有完全完成,只作代码记录,不作分析和展示,极其冗长,但里面有长按短按双击的复合,可以看看。 目录 题目代码底层驱动主程序核心代码关键:双击单击长按复合代码 …...
机器人动力学模型与MATLAB仿真
机器人刚体动力学由以下方程控制!!! startup_rvc mdl_puma560 p560.dyn 提前计算出来这些“disturbance”,然后在控制环路中将它“抵消”(有时候也叫前馈控制) 求出所需要的力矩,其中M项代表克服…...
SAPUI5基础知识3 - 引导过程(Bootstrap)
1. 背景 在上一篇博客中,我们已经建立出了第一个SAPUI5项目,接下来,我们将为这个项目添加引导过程。 在动手练习之前,让我们先解释一下什么引导过程。 1.1 什么是引导过程? 在计算机科学中,引导过程也称…...

ABAP 借助公司封装的钉钉URL,封装的RFC给钉钉发送消息
FUNCTION ZRFC_BC_SMSSEND_DINGTALK. *"---------------------------------------------------------------------- *"*"本地接口: *" IMPORTING *" VALUE(DESTUSRID) TYPE CHAR255 *" VALUE(CONTENT) TYPE CHAR255 *&quo…...

登录校验及全局异常处理器
登录校验 会话技术 会话:用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束.在一次会话中可以包含多次请求和响应会话跟踪:一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一浏览器,以便在同一次会话请求间共享数据会话跟踪方案 客户端…...
计算机视觉与模式识别实验1-2 图像的形态学操作
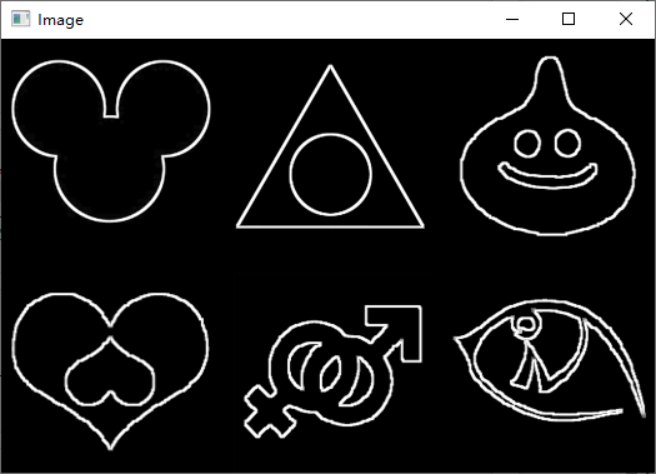
文章目录 🧡🧡实验流程🧡🧡1.图像膨胀2.图像腐蚀3.膨胀与腐蚀的综合使用4.对下面二值图像的目标提取骨架,并分析骨架结构。 🧡🧡全部代码🧡🧡 🧡🧡…...

【前端每日基础】day31——uni-app
uni-app 开发详细介绍 基本概念 uni-app:uni-app 是一个使用 Vue.js 开发多端应用的框架,可以编译到微信小程序、支付宝小程序、百度小程序、字节跳动小程序、H5、App等多个平台。 跨平台:一次开发,多端部署。通过条件编译实现多…...

云动态摘要 2024-05-31
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [1.5折起]年中盛惠--AI分会场 腾讯云 2024-05-30 人脸核身、语音识别、文字识别、数智人、腾讯混元等热门AI产品特惠,1.5折起 云服务器ECS试用产品续用 阿里云 2024-04-14 云…...

Oracle数据块如何存储真实数据
上周休假了几天,颓废了,没有输出。今天写一点内容。 先抛出一个问题。表中的数据在Oracle数据块中是如何存储的呢?今天简单说一下这个问题。通常数据库中的表会存储字符,数字,日期 这3种常见的数据类型。下面的例子就用这3种数据类型作说明 首先,Oracle数据块底层存储这…...

【WEB前端2024】开源智体世界:乔布斯3D纪念馆-第30课-门的移动动画
【WEB前端2024】开源智体世界:乔布斯3D纪念馆-第30课-门的移动动画 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。dtns.network是一款主要由JavaScript编写的智体世界引擎…...

智能化改造给企业带来的实际效果
1. 提高生产效率:通过自动化和智能化的生产线,减少人工操作,显著提升单位时间内的生产量。 2. 提升产品质量:智能化改造通过精确控制生产过程,减少人为错误,提高产品的一致性和可靠性。 3. 降低生产成本&am…...

深度学习-语言模型
深度学习-语言模型 统计语言模型神经网络语言模型语言模型的应用序列模型(Sequence Model)语言模型(Language Model)序列模型和语言模型的区别 语言模型(Language Model)是自然语言处理(NLP&…...

微型导轨在自动化制造中有哪些优势?
微型导轨在自动化制造中发挥重要作用,能够满足自动化设备制造中对精度要求较高的工艺环节。适用于自动装配线、自动检测设备和机器人操作等环节,推动了行业的进步与发展。那么,微型导轨在使用中有哪些优势呢? 1、精度高和稳定性强…...

探索气象数据的多维度三维可视化:PM2.5、风速与高度分析
探索气象数据的多维度可视化:PM2.5、风速与高度分析 摘要 在现代气象学中,数据可视化是理解复杂气象模式和趋势的关键工具。本文将介绍一种先进的数据可视化技术,它能够将PM2.5浓度、风速和高度等多维度数据以直观和动态的方式展现出来。 …...

【传知代码】双深度学习模型实现结直肠癌检测(论文复现)
前言:在医学领域,科技的进步一直是改变人类生活的关键驱动力之一。随着深度学习技术的不断发展,其在医学影像诊断领域的应用正日益受到关注。结直肠癌是一种常见但危害极大的恶性肿瘤,在早期发现和及时治疗方面具有重要意义。然而…...
平衡二叉树的应用举例
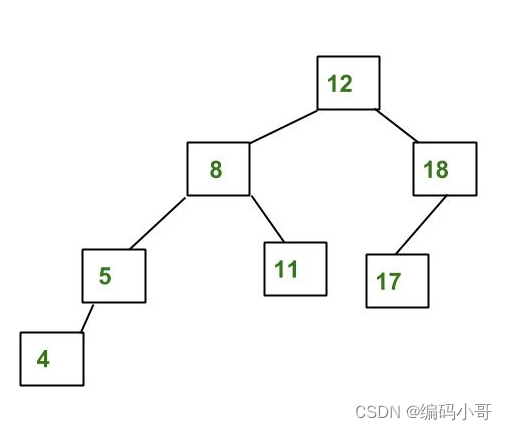
AVL 是一种自平衡二叉搜索树,其中任何节点的左右子树的高度之差不能超过 1。 AVL树的特点: 1、它遵循二叉搜索树的一般属性。 2、树的每个子树都是平衡的,即左右子树的高度之差最多为1。 3、当插入新节点时,树会自我平衡。因此…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
