Kotlin 对象
文章目录
- 对象表达式(匿名对象)
- 对象的声明
对象表达式(匿名对象)
在 Kotlin 中可以使用object {}声明一个匿名的对象,我们无需声明这个对象的类:
fun main() {val any = object {fun greet() = print("Hi")}any.greet()
}
Hi
在匿名对象中,我们不能声明抽象成员。
匿名对象可以继承自类或接口,默认情况下它的类型是Any,继承后它将可以是所继承的所有类型(如果显式声明其类型,它将是声明的类型):
open class Greeter {fun greet() = print("Hi")
}interface Runnable {fun run()
}fun main() {val any = object: Greeter(), Runnable {override fun run() = println("Run")}any.run()any.greet()
}
Run
Hi
对象的声明
我们可以使用object,像定义类class那样定义一个对象:
fun interface Runnable {fun run()
}object Greeter: Runnable {fun greet() = print("Hi")override fun run() = println("Run")
}fun main() {Greeter.run()Greeter.greet()
}
Run
Hi
对象没有构造函数,因为它不可被实例化。
对象中不能声明抽象方法,因为它不可被继承。
相关文章:

Kotlin 对象
文章目录 对象表达式(匿名对象)对象的声明 对象表达式(匿名对象) 在 Kotlin 中可以使用object {}声明一个匿名的对象,我们无需声明这个对象的类: fun main() {val any object {fun greet() print("…...

力扣 142题 环形链表Ⅱ 记录
题目描述 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内…...

乐观锁 or 悲观锁 你怎么选?
你有没有听过这样一句话:悲观者正确,乐观者成功。那么今天我来分享下什么是乐观锁和悲观锁。 乐观锁和悲观锁有什么区别,它们什么场景会用 乐观锁 乐观锁基于这样的假设:多个事务在同一时间对同一数据对象进行操作的可能性很…...

《庆余年算法番外篇》:范闲通过最短路径算法在阻止黑骑截杀林相
剧情背景 在《庆余年 2》22集中,林相跟大宝交代完为人处世的人生哲理之后,就要跟大宝告别了 在《庆余年 2》23集中,林相在告老还乡的路上与婉儿和大宝告别后 范闲也在与婉儿的对话中知道黑骑调动是绝密,并把最近一次告老还乡梅…...

大一C语言课设 服装销售系统 代码实现与项目总结
问题分析 服装信息管理及销售管理系统。方便对库存服装的信息管理和添加新服装数据,同时兼具库存数量管理功能。 功能实现 1、建立服装信息库,包括:服装代码、型号、规格、面料、颜色、单价、数量; 2、建立销售信息库ÿ…...
从新手到专家:深入探索JVM垃圾回收--开端篇
引言: 在Java的世界里,垃圾回收(Garbage Collection, GC)机制扮演着至关重要的角色,它决定了Java应用的性能、稳定性和扩展性。本系列文章旨在深入探讨JVM中的垃圾回收技术,从基础的概念讲起,直…...
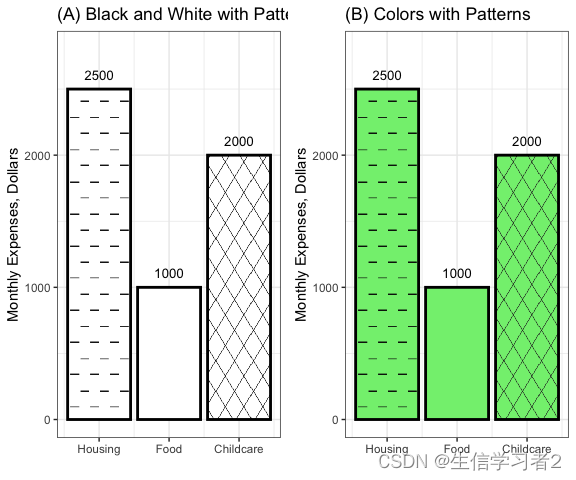
R可视化:另类的柱状图
介绍 方格状态的柱状图 加载R包 knitr::opts_chunk$set(echo TRUE, message FALSE, warning FALSE) library(patternplot) library(png) library(ggplot2) library(gridExtra)rm(list ls()) options(stringsAsFactors F)导入数据 data <- read.csv(system.file(&qu…...
Docker的数据管理(数据卷+数据卷容器)
文章目录 一、Docker的数据管理1、概述2、主要的技术(三种数据挂载方式)2.1、数据卷(Volumes)2.2、绑定挂载(Bind mounts)2.3、tmpfs挂载(Tmpfs mounts)2.4、之间的关系(…...
字符串-至多包含K种字符的子串中最长子串(mid)
一、题目描述 二、解题思路 借鉴以下题目思想,使用双指针,外层循环右侧指针移动,内存循环左侧指针移动 字符串-最长不含重复字符的子字符串(mid)-CSDN博客文章浏览阅读622次,点赞17次,收藏4次。java刷题:…...

Docker从安装开始精通
从虚拟机到容器 1.环境配置的难题 软件开发最大的麻烦事之一,就是环境配置。用户计算机的环境都不相同,你怎么知道自家的软件,能在那些机器跑起来? 用户必须保证两件事:操作系统的设置,各种库和组件的安装…...
)
MFC:初步理解序列化与反序列化(含代码实现)
序列化与反序列化是MFC将对象数据以二进制数据流的形式进行存储和读取的机制,读、写的效率很高。通过序列化与反序列化,可以将程序中对象在内存中数据保存到文件 (磁盘) 或者从文件 (磁盘) 中读取到内存以恢复对象数据,从而实现程序对数据的持…...

python程序控制结构
文章目录 一、python程序控制结构介绍二、顺序结构2.1、print()函数2.2、end参数2.3、input()函数 三、选择结构3.1选择结构的用途 四、循环结构4.1循环结构的构造4.1.1、循环结构的三个要素4.1.2、循环结构的一个要求4.1.3、循环结构的一个关系 4.2、循环语句4.2.1、while语句…...

【GD32】04 - Timer定时器
GD32中的定时器 GD32E230中有七个定时器,六种类型,其中通用的L4版本有两个,其他类型的各一个。 那我们就以通用L4这个类型来敲代码,其他流程是通用的。 通用L4 虽然每种类型的定时器都有自己的结构框图,但是其实大差…...

Golang | Leetcode Golang题解之第123题买卖股票的最佳时机III
题目: 题解: func maxProfit(prices []int) int {buy1, sell1 : -prices[0], 0buy2, sell2 : -prices[0], 0for i : 1; i < len(prices); i {buy1 max(buy1, -prices[i])sell1 max(sell1, buy1prices[i])buy2 max(buy2, sell1-prices[i])sell2 m…...
Leetcode2028. 找出缺失的观测数据
Every day a Leetcode 题目来源:2028. 找出缺失的观测数据 解法1:模拟 统计当前 m 个元素的总和 curSum sum(rolls),总共 mn 个元素和为 total (m n) * mean。 排除 2 种情况: total - curSum > 6 * n:n 个…...

如何在CentOS中合理划分磁盘空间以优化系统性能
目录 前言 理想的分区方案 为什么需要单独分区 安全性 性能 管理和维护 稳定性和可靠性 升级和兼容性 结论 前言 在进行CentOS系统的安装和配置时,合理划分磁盘空间是确保系统性能、安全性和易于管理的关键步骤。本文将探讨如何根据系统的硬件配置和预期用途…...
算法(十一)贪婪算法
文章目录 算法简介算法概念算法举例 经典问题 -背包问题 算法简介 算法概念 贪婪算法(Greedy)是一种在每一步都采取当前状态下最好的或者最优的选择,从而希望导致结果也是全局最好或者最优的算法。贪婪算法是当下局部的最优判断,…...
Rust之函数式语言特性:迭代器和闭包(一):概述
开发环境 Windows 11Rust 1.78.0 VS Code 1.89.1 项目工程 这次创建了新的工程minigrep. 函数式语言特性:迭代器和闭包 Rust的设计从许多现有语言和技术中获得了灵感,其中一个重要影响是函数式编程。函数式编程通常包括通过在参数中传递函数、从其他函数返回函数、…...

配置资源管理
一 Secret Secret 是用来保存密码、token、密钥等敏感数据的 k8s 资源,这类数据虽然也可以存放在 Pod 或者镜像中,但是放在 Secret 中是为了更方便的控制如何使用数据,并减少暴露的风险。 1 有三种类型: kubernetes.io/service…...
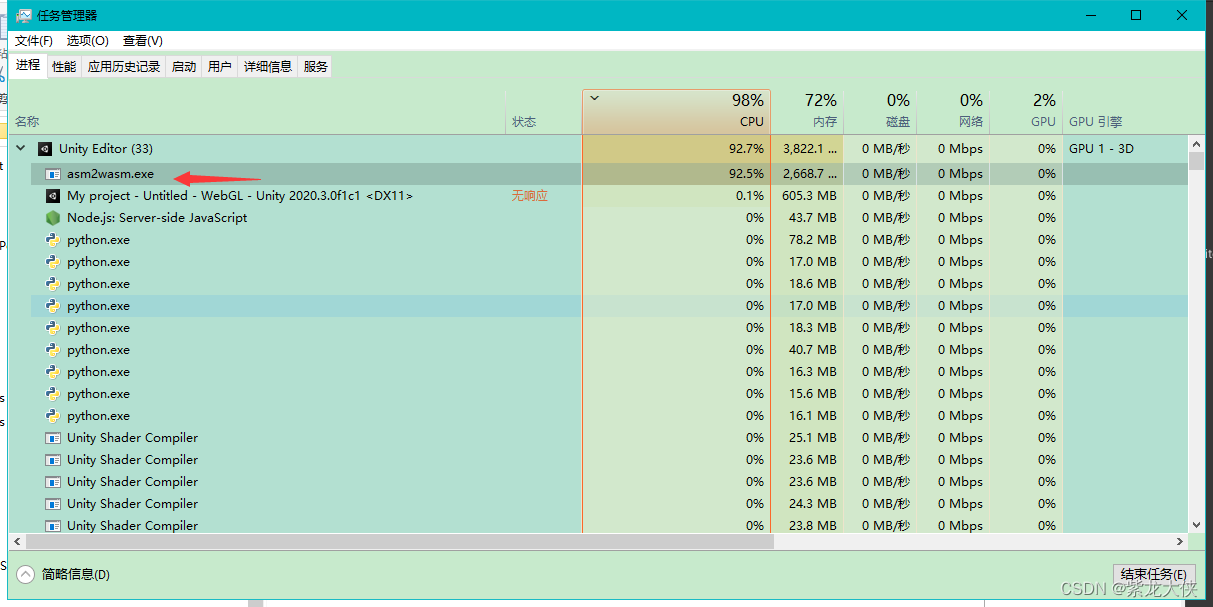
unity2020打包webGL时卡进程问题
我使用的2020.3.0f1c1,打包发布WEB版的时候会一直卡到asm2wasm.exe这个进程里,而且CPU占用率90%以上。 即使是打包一个新建项目的空场景也是同样的问题,我尝试过一直卡在这里会如何,结果还真打包成功了。只是打包一个空场景需要20…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
