Leetcode2028. 找出缺失的观测数据
Every day a Leetcode
题目来源:2028. 找出缺失的观测数据
解法1:模拟
统计当前 m 个元素的总和 curSum = sum(rolls),总共 m+n 个元素和为 total = (m + n) * mean。
排除 2 种情况:
- total - curSum > 6 * n:n 个骰子全丢 6 都补不了 total 和 curSum 的差距。
- total - curSum < 1 * n:n 个骰子的最小点数和为 n,如果 total - curSum 小于 n,说明数据不合法。
我的答案数组的构造方法:
每个骰子先分配 (total - curSum) / n 个点数,再将 (total - curSum) % n 个骰子的点数加 1。
代码:
/** @lc app=leetcode.cn id=2028 lang=cpp** [2028] 找出缺失的观测数据*/// @lc code=start
class Solution
{
public:vector<int> missingRolls(vector<int> &rolls, int mean, int n){int m = rolls.size();int curSum = accumulate(rolls.begin(), rolls.end(), 0);int total = (m + n) * mean;if (total - curSum > 6 * n || total - curSum < 1 * n)return {};vector<int> ans(n, (total - curSum) / n);for (int i = 0; i < (total - curSum) % n; i++)ans[i]++;return ans;}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(m),其中 m 是数字 rolls 的长度。
空间复杂度:O(n)。
相关文章:

Leetcode2028. 找出缺失的观测数据
Every day a Leetcode 题目来源:2028. 找出缺失的观测数据 解法1:模拟 统计当前 m 个元素的总和 curSum sum(rolls),总共 mn 个元素和为 total (m n) * mean。 排除 2 种情况: total - curSum > 6 * n:n 个…...

如何在CentOS中合理划分磁盘空间以优化系统性能
目录 前言 理想的分区方案 为什么需要单独分区 安全性 性能 管理和维护 稳定性和可靠性 升级和兼容性 结论 前言 在进行CentOS系统的安装和配置时,合理划分磁盘空间是确保系统性能、安全性和易于管理的关键步骤。本文将探讨如何根据系统的硬件配置和预期用途…...
算法(十一)贪婪算法
文章目录 算法简介算法概念算法举例 经典问题 -背包问题 算法简介 算法概念 贪婪算法(Greedy)是一种在每一步都采取当前状态下最好的或者最优的选择,从而希望导致结果也是全局最好或者最优的算法。贪婪算法是当下局部的最优判断,…...
Rust之函数式语言特性:迭代器和闭包(一):概述
开发环境 Windows 11Rust 1.78.0 VS Code 1.89.1 项目工程 这次创建了新的工程minigrep. 函数式语言特性:迭代器和闭包 Rust的设计从许多现有语言和技术中获得了灵感,其中一个重要影响是函数式编程。函数式编程通常包括通过在参数中传递函数、从其他函数返回函数、…...

配置资源管理
一 Secret Secret 是用来保存密码、token、密钥等敏感数据的 k8s 资源,这类数据虽然也可以存放在 Pod 或者镜像中,但是放在 Secret 中是为了更方便的控制如何使用数据,并减少暴露的风险。 1 有三种类型: kubernetes.io/service…...
unity2020打包webGL时卡进程问题
我使用的2020.3.0f1c1,打包发布WEB版的时候会一直卡到asm2wasm.exe这个进程里,而且CPU占用率90%以上。 即使是打包一个新建项目的空场景也是同样的问题,我尝试过一直卡在这里会如何,结果还真打包成功了。只是打包一个空场景需要20…...

云原生架构相关技术_3.无服务器技术
1.技术特点 1.1面向特定领域的后端云服务(BaaS) 随着以Kubernetes为代表的云原生技术成为云计算的容器界面,Kubernetes成为云计算的新一代操作系统。面向特定领域的后端云服务(BaaS)则是这个操作系统上的服务API&…...
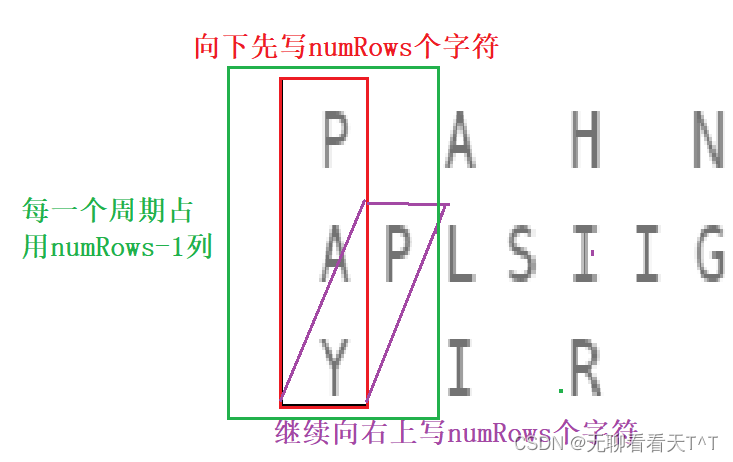
Leetcode:Z 字形变换
题目链接:6. Z 字形变换 - 力扣(LeetCode) 普通版本(二维矩阵的直接读写) 解决办法:直接依据题目要求新建并填写一个二维数组,最后再将该二维数组中的有效字符按从左到右、从上到下的顺序读取并…...

Python 3 判断文件是否存在
1 使用os.path模块 import osfile_path hello.txtif os.path.exists(file_path):print(f"文件 {file_path} 存在。") else:print(f"文件 {file_path} 不存在。") 2 使用pathlib模块 from pathlib import Pathfile_path Path(word.txt)if file_path.ex…...

(深度学习记录)第TR3周:Transformer 算法详解
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 文本的输入处理中,transformer会将输入文本序列的每个词转化为一个词向量,我们通常会选择一个合适的长度作为输入…...

谷神前端组件增强:自定义列
初始化 $gp.customColumn {}initColumnPool /*** initColumnPool* 初始化列池* * param prefix 前缀* param length 长度* * return Array 列ID数组* */ function initColumnPool (prefix, length) {return Array.from({length}, (value, index) > prefix index) } self…...
)
31-ESP32-S3-WIFI篇-02 Event Group (事件标记组)
ESP32-S3-WIFI 事件标记组 介绍 在ESP32-S3的WiFi驱动程序中,事件标记组(Event Group)是一个非常重要的概念。它是FreeRTOS中的一种同步机制,用于在任务之间传递和同步事件。在WiFi驱动程序中,我们使用事件标记组来通…...

构建企业级AI私有知识库
一、引言 在当今竞争激烈的市场环境中,企业为了保持竞争优势,需要高效地管理和利用内部知识资源。构建一个企业级AI私有知识库,不仅可以集中存储和管理企业知识,还能通过人工智能技术实现知识的智能化处理和利用。本文将详细介绍…...

C语言王国——杨氏矩阵
目录 1. 引言 2. 了解杨氏矩阵 3. 思路分析 4. 代码 5. 总结 1. 引言 最近在做二维数组的训练的时候发现了一个很有意思的题: 一看这不是杨氏矩阵嘛,接下来就由姜糖我带大家了解一下这个著名的矩阵。 2. 了解杨氏矩阵 通过查阅百度得知: …...

陪玩小程序都需要怎么做?
开发陪玩小程序需要进行全面的需求分析、功能规划、技术选型、界面设计等一系列步骤。陪玩小程序作为一种新兴的网络服务平台,为用户提供了寻找游戏伙伴、预约陪玩服务等功能,满足了用户在游戏领域的社交互动和技能提升需求。具体分析如下: 需…...
)
postgressql——子事务可见性判断 性能问题(8)
子事务可见性判断 & 性能 测试SQL BEGIN; PREPARE sel(integer) ASSELECT count(*)FROM contendWHERE id BETWEEN $1 AND $1 + 100; PREPARE upd(integer) ASUPDATE contend SET val = val + 1WHERE id IN ($1, $1 + 10, $1 + 20, $1 + 30);SAVEPOINT a; \set rnd random…...

20240531在飞凌的OK3588-C开发板上跑原厂的Buildroot测试USB摄像头
20240531在飞凌的OK3588-C开发板上跑原厂的Buildroot测试USB摄像头 2024/5/31 20:04 USB摄像头分辨率:1080p(1920x1080) 默认编译Buildroot的SDK即可点亮USB摄像头。v4l2-ctl --list-devices v4l2-ctl --list-formats-ext -d /dev/video74 …...

从0开始学统计-什么是回归?
1.什么是回归? 回归(Regression)是统计学中一种用于探索变量之间关系的分析方法。它主要用于预测一个或多个自变量(输入变量)与因变量(输出变量)之间的关系。在回归分析中,我们尝试根…...
Element-ui使用上传时弹框选择文件类型
实现效果 1,点击上传,上传文件; 2,选择文件; 3,弹框选择文件类型; 4,选择类型后确定上传; 一,上传 跳过; 二,定义弹框下拉框…...

原生小程序一键获取手机号
1.效果图 2.代码index.wxml <!-- 获取手机号 利用手机号快速填写的功能,将button组件 open-type 的值设置为 getPhoneNumber--><button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber">获取手机号</button> …...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
