【数据结构】详解二叉树
文章目录
- 1.树的结构及概念
- 1.1树的概念
- 1.2树的相关结构概念
- 1.3树的表示
- 1.4树在实际中的应用
- 2.二叉树的结构及概念
- 2.1二叉树的概念
- 2.2特殊的二叉树
- 2.2.1满二叉树
- 2.2.2完全二叉树
- 2.3 二叉树的性质
- 2.4二叉树的存储结构
- 2.4.1顺序结构
- 2.4.2链表结构
1.树的结构及概念
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根结点没有前驱结点除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的
1.2树的相关结构概念
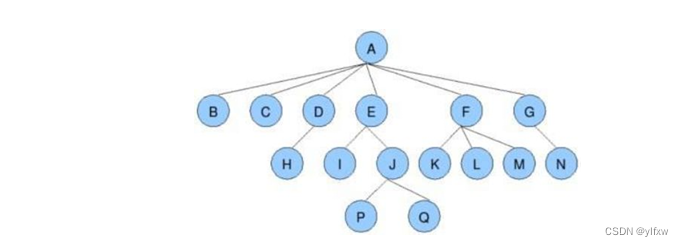
在一个树中,有下面几种结构概念:
结点的度:一个结点含有的子树的个数称为该结点的度; 如上图:A的为6,我们用一张图来更好的了解:
叶结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等结点为叶结点
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等结点为分支结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
树的度:一棵树中,最大的结点的度称为树的度; 如上图:树的度为6
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
这里面的概念我们不需要全都记住,标黄的需要我们重点关注以下;
1.3树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点 struct Node* pNextBrother; // 指向其下一个兄弟结点 DataType data; // 结点中的数据域
};
在这个方法中,我们用firstchild指针找当前节点的第一个孩子节点(A),再用pnextbrother指针找到后续的孩子节点(B,C)找完之后接着用firstchild找到D,然后重复上面的操作,直到找完为止;
1.4树在实际中的应用
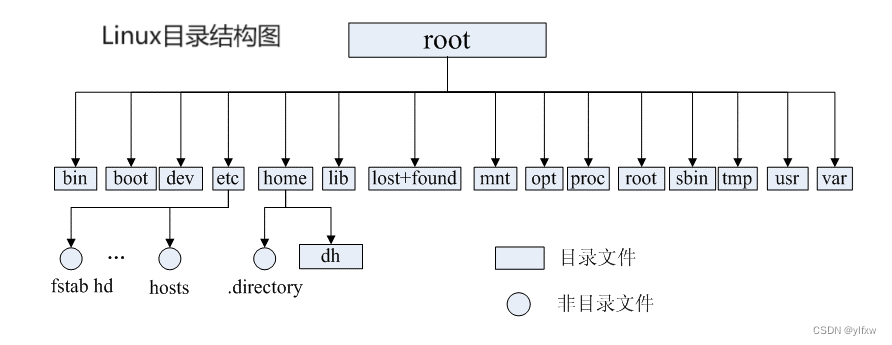
2.二叉树的结构及概念
2.1二叉树的概念
二叉树(Binary Tree) 是由n个结点构成的有限集(n≥0),该集合:
- 或者为空;
- 由一个根结点加上两棵别称为左子树和右子树的二叉树组成;
由上图我们可以得知:
1.一个二叉树不存在度大于2的结点。
2.二是结点的子树有左右之分,不能随意调换,调换后又是一棵新的二叉树。
对于任意一个二叉树都是由以下几种情况复合而成的;
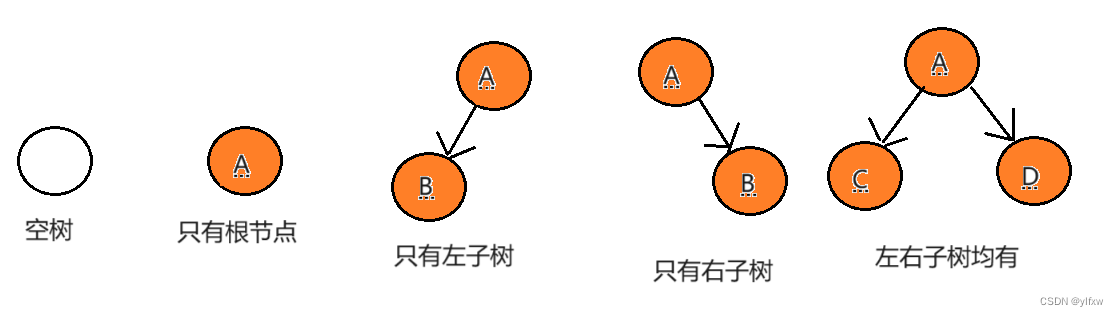
2.2特殊的二叉树
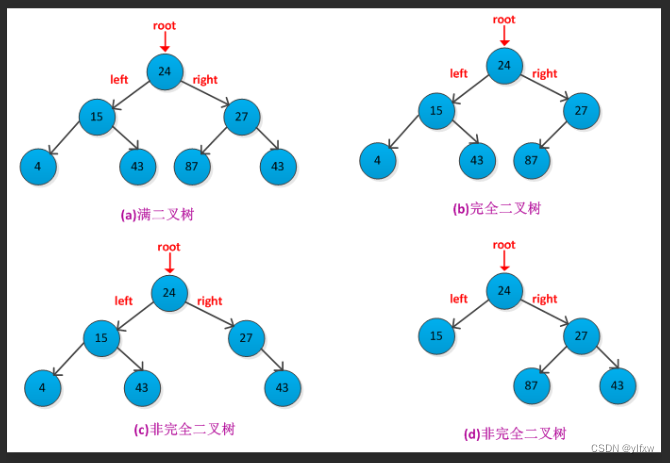
2.2.1满二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是,则它就是满二叉树。
2.2.2完全二叉树
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
** 要注意的是满二叉树是一种特殊的完全二叉树**。
2.3 二叉树的性质
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^( i-1) 个结点.
- 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是2^h -1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n,度为2的分支结点个数为 m
,则有n=m+1;- 若规定根结点的层数为1,具有n个结点的满二叉树的深度,h= . (ps:是log以2
为底,n+1为对数)- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对
于序号为i的结点有:
. 1.若i>0,i位置结点的双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点;
. 2.若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子;
. 3.若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子;
2.4二叉树的存储结构
2.4.1顺序结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
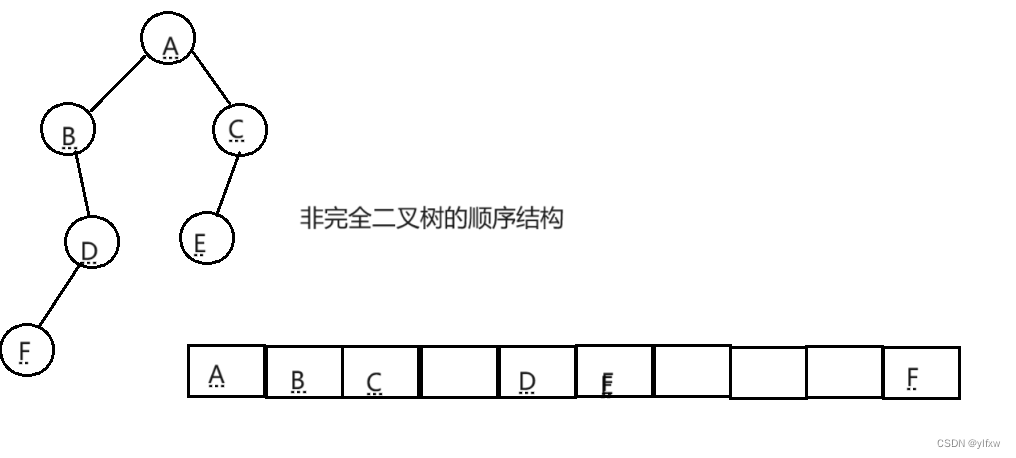
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空
间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺
序存储在物理上是一个数组,在逻辑上是一颗二叉树。

2.4.2链表结构
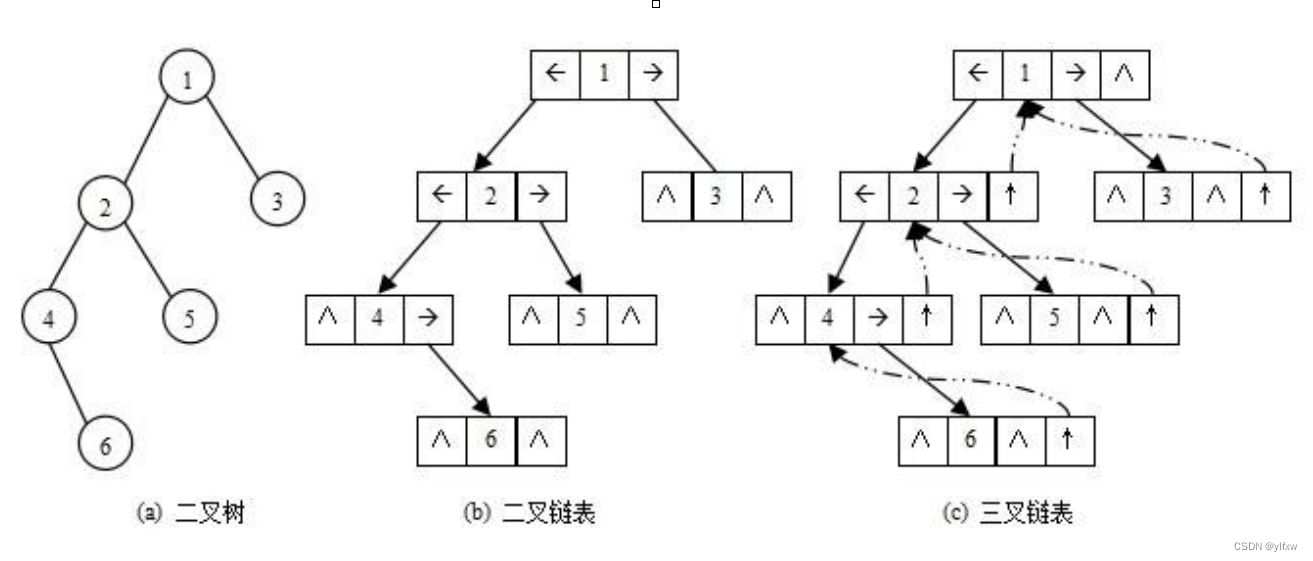
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是:
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面学到高阶数据结构如红黑树等会用到三叉链。
相关文章:
【数据结构】详解二叉树
文章目录 1.树的结构及概念1.1树的概念1.2树的相关结构概念1.3树的表示1.4树在实际中的应用 2.二叉树的结构及概念2.1二叉树的概念2.2特殊的二叉树2.2.1满二叉树2.2.2完全二叉树 2.3 二叉树的性质2.4二叉树的存储结构2.4.1顺序结构2.4.2链表结构 1.树的结构及概念 1.1树的概念…...

MapDB:轻量级、高性能的Java嵌入式数据库引擎
MapDB:轻量级、高性能的Java嵌入式数据库引擎 在今天的软件开发中,嵌入式数据库因其轻便、高效和易于集成而备受欢迎。对于Java开发者来说,MapDB无疑是一个值得关注的选项。MapDB是一个纯Java编写的嵌入式数据库引擎,它提供了高性…...

Rye: 一个革新的Python包管理工具
文章目录 Rye: 一个革新的Python包管理工具Rye的诞生背景Rye的核心特性Rye的安装与使用Rye的优势与挑战Rye的未来展望结语 Rye: 一个革新的Python包管理工具 在Python生态系统中,包管理一直是一个复杂且令人头疼的问题。随着Python社区的不断发展,出现了…...

如何在C#代码中判断当前C#的版本和dotnet版本
代码如下: using System.Reflection; using System.Runtime.InteropServices;var csharpVersion typeof(string).Assembly.GetCustomAttributes(typeof(AssemblyFileVersionAttribute), false).OfType<AssemblyFileVersionAttribute>().FirstOrDefault()?.…...
Linux 36.3@Jetson Orin Nano之系统安装
Linux 36.3Jetson Orin Nano之系统安装 1. 源由2. 命令行烧录Step 1:下载Linux 36.3安装程序Step 2:下载Linux 36.3根文件系统Step 3:解压Linux 36.3安装程序Step 4:解压Linux 36.3根文件系统Step 5:安装应用程序Step …...
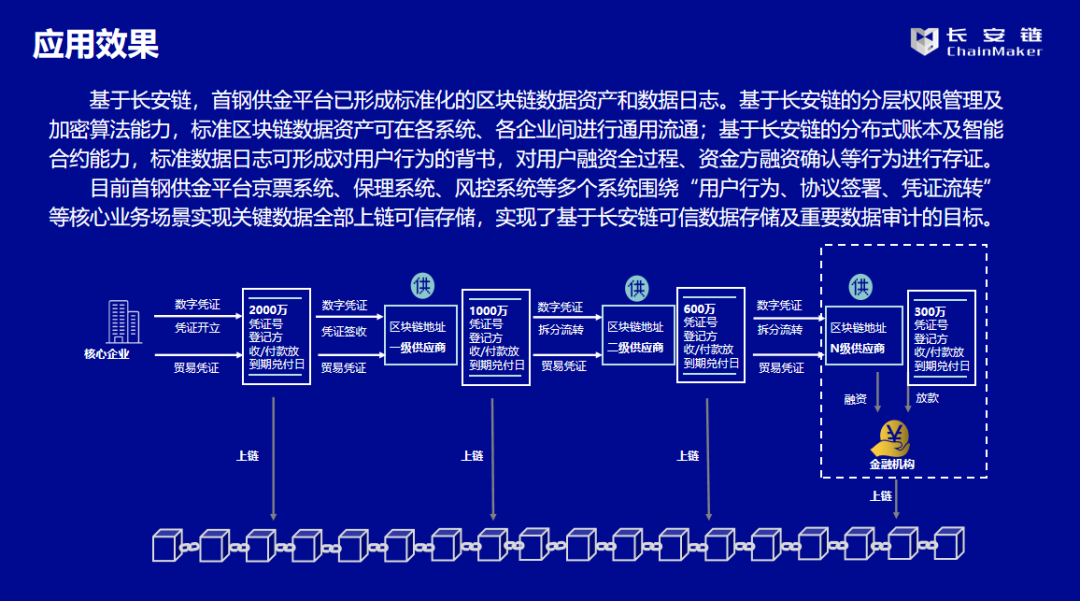
案例实践 | 基于长安链的首钢供应链金融科技服务平台
案例名称-首钢供应链金融科技服务平台 ■ 建设单位 首惠产业金融服务集团有限公司 ■ 用户群体 核心企业、资金方(多为银行)等合作方 ■ 应用成效 三大业务场景,共计关联29个业务节点,覆盖京票项目全部关键业务 案例背景…...
—Vue3.4新特性揭秘:defineModel重塑v-model,拥抱高效双向数据流!)
Vue3实战笔记(55)—Vue3.4新特性揭秘:defineModel重塑v-model,拥抱高效双向数据流!
文章目录 前言defineModel() 基本用法总结 前言 v-model 可以在组件上使用以实现双向绑定。 从 Vue 3.4 开始,推荐的实现方式是使用 defineModel() 宏 defineModel() 基本用法 定义defineModel(): <!-- Child.vue --> <script setup> con…...

C++ | Leetcode C++题解之第123题买卖股票的最佳时机III
题目: 题解: class Solution { public:int maxProfit(vector<int>& prices) {int n prices.size();int buy1 -prices[0], sell1 0;int buy2 -prices[0], sell2 0;for (int i 1; i < n; i) {buy1 max(buy1, -prices[i]);sell1 max(…...

微信小程序中Button组件的属性值和用法详解
在微信小程序开发中,Button组件是非常常用的UI组件之一,它可以让用户进行交互操作,比如提交表单、跳转页面等。了解Button组件的属性值和用法对于开发者来说至关重要。 1. Button组件简介 简要介绍Button组件在小程序中的作用和重要性&…...

等保测评 | 等保测评简介及流程具体是什么?
等保测评是指对信息系统进行安全性评估和测试,以确保其符合国家相关等级保护要求。在当前信息时代,各类机构和企业面临着日益严峻的网络安全风险,等保测评成为了保障信息系统安全的重要手段之一。本文将介绍等保测评的基本概念、流程和重要性…...
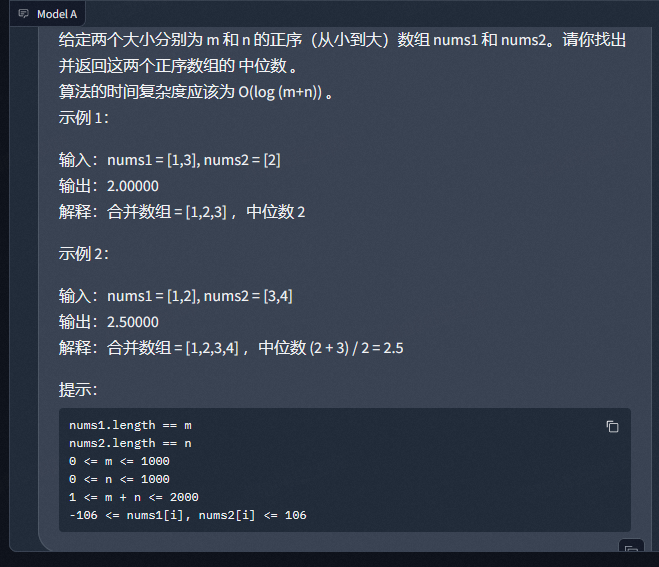
CompassArena 司南大模型测评--代码编写
测试角度 要说测试模型,对咱们程序员来说,那自然是写代码的能力强不强比较重要了。那么下面我们以 leetcode 中的一道表面上是困难题的题目来考考各家大模型,看看哪个才应该是咱们日常写程序的帮手。 部分模型回答 问题部分如下截图&#…...

叉积和法向量学习笔记
目录 叉积用的内积 相似点 给定平面上的两个向量 A 和 B,叉积和法向量相等吗 理解这点的关键: 结论: 叉积判断平面内两个向量是否相交 叉积(Cross Product)和法向量(Normal Vector)确实有…...

YZW900规格书
title: “深圳市沃进科技有限公司” 深圳市沃进科技有限公司 TOP视图 特性 异地组网,远程访问有线/无线备份单模双卡备份5G转有线,5G转WIFI2.4G5.8G双频WIFI三网口,WAN/LAN可切换软硬件看门狗智能防掉线云平台、客户端远程管理安装支架安装铝…...

9岁学生学什么编程好一些:探索编程启蒙的奥秘
9岁学生学什么编程好一些:探索编程启蒙的奥秘 在数字时代,编程已逐渐成为一项基本技能。对于9岁的学生来说,选择适合的编程课程或平台,对于培养逻辑思维、创新思维以及解决问题的能力至关重要。那么,9岁学生学什么编程…...

Java反射实战指南:反射机制的终极指南
1. 反射机制简介 在Java中,反射机制提供了一种强大的工具,用于在运行时检查类、接口、字段和方法。但它的重要性不止于此,它允许程序动态加载、探索和使用编译时完全未知的代码。这种能力是Java语言支持的一种“动态”特性,使得J…...

高效训练超越LoRA,北航发布MoRA
什么!LoRA我都没有学懂,又出现了MoRA??? LoRA作为当下最火热的大语言模型参数高效微调技术,正在以前所未有的速度迭代更新。从最初的LoRA到陆续推出的LoRA、DoRA、AsyLoRA等变体,LoRA家族可谓是…...
)
【Spring】Spring之依赖注入源码解析(上)
目录 Spring中到底有几种依赖注入的方式? 手动注入 自动注入 XML的autowire自动注入 Autowired注解的自动注入 寻找注入点 桥接方法 注入点进行注入 字段注入 Set方法注入 Spring中到底有几种依赖注入的方式? 首先分两种: 手动注…...

HBase 常用 shell 操作
下面给大家介绍一些HBase 常用 shell 操作,各位看官看好了啦,我要献丑了。 进入 HBase 客户端命令操作界面 $ bin/hbase shell查看帮助命令 > help查看当前数据库中有哪些表 > list创建一张表 创建 user 表,包含 info、data 两个列…...

【区分vue2和vue3下的element UI InputNumber 计数器组件,分别详细介绍属性,事件,方法如何使用,并举例】
在 Vue 2 中,Element UI 提供了 el-input-number 组件作为计数器组件,用于处理数字输入。而在 Vue 3 中,Element Plus 同样提供了类似的组件,但可能有一些属性、事件或方法的细微差异。下面我将分别介绍 Vue 2 的 Element UI 和 V…...

科普健康短视频:成都鼎茂宏升文化传媒公司
科普健康短视频:引领健康知识新潮流 在数字化时代的浪潮中,短视频以其短小精悍、直观易懂的特点,迅速成为大众获取信息的重要渠道。其中,科普健康短视频更是凭借其科学、权威、实用的内容,吸引了大量关注健康的观众。…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...



