叉积和法向量学习笔记
目录
叉积用的内积
相似点
给定平面上的两个向量 A 和 B,叉积和法向量相等吗
理解这点的关键:
结论:
叉积判断平面内两个向量是否相交
叉积(Cross Product)和法向量(Normal Vector)确实有一些相似之处,尤其是在计算和应用方面。以下是它们的主要相似点:
叉积用的内积

相似点
-
三维空间中的关联性:
- 叉积主要在三维空间中定义和应用。
- 法向量通常也是在三维空间中定义的,特别是在描述平面或曲面时。
-
计算方法:
- 叉积是计算两个向量的乘积,其结果是一个向量,该向量垂直于原来的两个向量所在的平面。
- 法向量可以通过两个非平行向量的叉积来计算。例如,给定平面上的两个向量 A 和 B,它们的叉积 A × B 就是该平面的一个法向量。
-
方向:
- 叉积结果的方向由右手定则确定,垂直于参与叉积的两个向量。
- 法向量的方向也是垂直于描述的表面,可以通过右手定则来确定它的具体方向。
-
应用:
- 叉积广泛用于计算物理学中的力矩、角动量等问题。
- 法向量在计算几何中用于确定平面的方向、计算光线与表面的交点、反射和折射等问题。
给定平面上的两个向量 A 和 B,叉积和法向量相等吗
在三维空间中,给定平面上的两个向量 A 和 B,它们的叉积 A × B 与这个平面的法向量具有相同的方向,但其大小(长度)可能不同,因此它们在数学上并不是完全相等的,但方向相同。
理解这点的关键:
-
方向:
- 叉积 A × B 的方向是垂直于向量 A 和 B 所在的平面。根据右手定则,若用右手的食指指向 A,中指指向 B,则叉积 A × B 的方向由拇指指向,这个方向就是法向量的方向。
-
大小:
- 叉积 A × B 的大小等于 A 和 B 的长度乘积再乘以它们夹角的正弦值: ∥A×B∥=∥A∥∥B∥sin(θ)\|\mathbf{A} \times \mathbf{B}\| = \|\mathbf{A}\| \|\mathbf{B}\| \sin(\theta)∥A×B∥=∥A∥∥B∥sin(θ) 其中 θ\thetaθ 是向量 A 和 B 之间的夹角。
- 法向量的大小可以是任意的,因为法向量的关键属性是它的方向,而不是它的大小。
结论:
- 相同方向:叉积 A × B 和法向量的方向相同,都是垂直于 A 和 B 所在的平面。
- 大小不同:叉积 A × B 的大小依赖于 A 和 B 的长度及其夹角的正弦值,而法向量的大小可以缩放到任意值。
因此,可以说叉积 A × B 是法向量的一个实例,但大小可能不同。通俗地说,叉积给出了一个特定大小的法向量,但平面的法向量可以是任何大小,只要方向一致即可。
叉积判断平面内两个向量是否相交
def cross_product_sign(A, B, C):"""计算向量 AB 和 AC 的叉积的符号。参数:A, B, C: 二维平面上的点,格式为 (x, y)返回值:叉积的符号:正数、负数或零"""return (B[0] - A[0]) * (C[1] - A[1]) - (B[1] - A[1]) * (C[0] - A[0])def is_point_on_segment(P, A, B):"""判断点 P 是否在线段 AB 上。参数:P, A, B: 二维平面上的点,格式为 (x, y)返回值:True 表示点 P 在线段 AB 上,False 表示不在"""return min(A[0], B[0]) <= P[0] <= max(A[0], B[0]) and min(A[1], B[1]) <= P[1] <= max(A[1], B[1])def do_segments_intersect(A, B, C, D):"""判断两个线段 AB 和 CD 是否相交。参数:A, B, C, D: 二维平面上的点,格式为 (x, y)返回值:True 表示线段相交,False 表示不相交"""# 计算叉积的符号d1 = cross_product_sign(A, B, C)d2 = cross_product_sign(A, B, D)d3 = cross_product_sign(C, D, A)d4 = cross_product_sign(C, D, B)# 检查叉积符号是否不同if d1 * d2 < 0 and d3 * d4 < 0:return True# 特殊情况:线段共线并重叠if d1 == 0 and is_point_on_segment(C, A, B):return Trueif d2 == 0 and is_point_on_segment(D, A, B):return Trueif d3 == 0 and is_point_on_segment(A, C, D):return Trueif d4 == 0 and is_point_on_segment(B, C, D):return Truereturn False# 示例线段
A = (1, 1)
B = (4, 4)
C = (1, 4)
D = (4, 1)# 判断线段是否相交
print("线段 AB 和 CD 是否相交:", do_segments_intersect(A, B, C, D)) # 输出 True# 不相交的示例
E = (1, 1)
F = (2, 2)
G = (3, 3)
H = (4, 4)print("线段 EF 和 GH 是否相交:", do_segments_intersect(E, F, G, H)) # 输出 False
相关文章:

叉积和法向量学习笔记
目录 叉积用的内积 相似点 给定平面上的两个向量 A 和 B,叉积和法向量相等吗 理解这点的关键: 结论: 叉积判断平面内两个向量是否相交 叉积(Cross Product)和法向量(Normal Vector)确实有…...

YZW900规格书
title: “深圳市沃进科技有限公司” 深圳市沃进科技有限公司 TOP视图 特性 异地组网,远程访问有线/无线备份单模双卡备份5G转有线,5G转WIFI2.4G5.8G双频WIFI三网口,WAN/LAN可切换软硬件看门狗智能防掉线云平台、客户端远程管理安装支架安装铝…...

9岁学生学什么编程好一些:探索编程启蒙的奥秘
9岁学生学什么编程好一些:探索编程启蒙的奥秘 在数字时代,编程已逐渐成为一项基本技能。对于9岁的学生来说,选择适合的编程课程或平台,对于培养逻辑思维、创新思维以及解决问题的能力至关重要。那么,9岁学生学什么编程…...

Java反射实战指南:反射机制的终极指南
1. 反射机制简介 在Java中,反射机制提供了一种强大的工具,用于在运行时检查类、接口、字段和方法。但它的重要性不止于此,它允许程序动态加载、探索和使用编译时完全未知的代码。这种能力是Java语言支持的一种“动态”特性,使得J…...

高效训练超越LoRA,北航发布MoRA
什么!LoRA我都没有学懂,又出现了MoRA??? LoRA作为当下最火热的大语言模型参数高效微调技术,正在以前所未有的速度迭代更新。从最初的LoRA到陆续推出的LoRA、DoRA、AsyLoRA等变体,LoRA家族可谓是…...
)
【Spring】Spring之依赖注入源码解析(上)
目录 Spring中到底有几种依赖注入的方式? 手动注入 自动注入 XML的autowire自动注入 Autowired注解的自动注入 寻找注入点 桥接方法 注入点进行注入 字段注入 Set方法注入 Spring中到底有几种依赖注入的方式? 首先分两种: 手动注…...

HBase 常用 shell 操作
下面给大家介绍一些HBase 常用 shell 操作,各位看官看好了啦,我要献丑了。 进入 HBase 客户端命令操作界面 $ bin/hbase shell查看帮助命令 > help查看当前数据库中有哪些表 > list创建一张表 创建 user 表,包含 info、data 两个列…...

【区分vue2和vue3下的element UI InputNumber 计数器组件,分别详细介绍属性,事件,方法如何使用,并举例】
在 Vue 2 中,Element UI 提供了 el-input-number 组件作为计数器组件,用于处理数字输入。而在 Vue 3 中,Element Plus 同样提供了类似的组件,但可能有一些属性、事件或方法的细微差异。下面我将分别介绍 Vue 2 的 Element UI 和 V…...

科普健康短视频:成都鼎茂宏升文化传媒公司
科普健康短视频:引领健康知识新潮流 在数字化时代的浪潮中,短视频以其短小精悍、直观易懂的特点,迅速成为大众获取信息的重要渠道。其中,科普健康短视频更是凭借其科学、权威、实用的内容,吸引了大量关注健康的观众。…...
Amis源码构建 sdk版本
建议在linux环境下构建(mac环境下也可以),需要用到sh脚本(amis/build.sh)。 Js sdk打包是基于fis进行编译打包的,具体可见fis-conf.js: amis-master源码下载:https://github.com/baidu/amis g…...
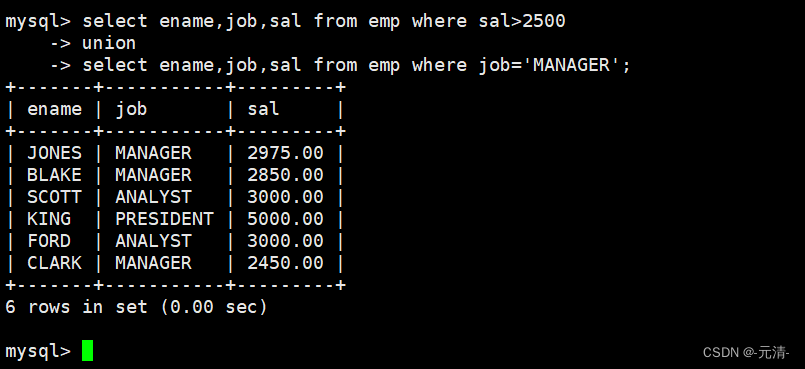
【MySQL数据库】:MySQL复合查询
目录 基本查询回顾 多表查询 自连接 子查询 单行子查询 多行子查询 多列子查询 在from子句中使用子查询 合并查询 前面我们讲解的mysql表的查询都是对一张表进行查询,在实际开发中这远远不够。 基本查询回顾 【MySQL数据库】:MySQL基本查…...
PS Mac Photoshop 2024 for Mac[破]图像处理软件[解]PS 2024安装教程[版]
Mac分享吧 文章目录 效果一、准备工作二、开始安装1、Anticc简化版安装1.1双击运行软件,安装1.2 解决来源身份不明的开发者问题**此代码为打开:系统偏好设置 – 隐私与安全性,中的【任何来源】,如下图:**1.3 再次运行…...

深入URP之Shader篇16: UNITY_BRANCH和UNITY_FLATTEN
Shader中的if分支 我们在shader中写if语句,例如: if(a>0){//do some cool thing }else{//do other cool thing }实际上,编译器会进行优化,以及处理成多种不同的情况。比如编译器会将if和else展开,分别执行其中的代…...
5.25.1 用于组织病理学图像分类的深度注意力特征学习
提出了一种基于深度学习的组织病理学图像分类新方法。我们的方法建立在标准卷积神经网络 (CNN) 的基础上,并结合了两个独立的注意力模块,以实现更有效的特征学习。 具体而言,注意力模块沿不同维度推断注意力图,这有助于将 CNN 聚焦于关键图像区域,并突出显示判别性特征通…...

uni-app+php 生成微信二维码 分销海报
主要代码如下,可直接复制调试参数: //查询当前用户是否有分销海报public function user_poster(){$this->checkAuth();//查询会员信息$user $this->getUserInfoById($this->user_id);if(!empty($user[distribution_img])){$result[data] $use…...

已解决java.lang.annotation.AnnotationFormatError: 注解格式错误的正确解决方法,亲测有效!!!
已解决java.lang.annotation.AnnotationFormatError: 注解格式错误的正确解决方法,亲测有效!!! 亲测有效 报错问题解决思路 解决方法解决方法1. 检查注解定义2. 验证注解使用位置3. 检查注解参数4. 更新依赖库5. 示例代码 解决思路…...
使用 EBS 和构建数据库服务器并使用应用程序与数据库交互
实验 4:使用 EBS 实验概览 本实验着重介绍 Amazon Elastic Block Store (Amazon EBS),这是一种适用于 Amazon EC2 实例的重要底层存储机制。在本实验中,您将学习如何创建 Amazon EBS 卷、将其附加到实例、向卷应用文件系统,然后进…...
pom文件新增依赖时异常问题定位技巧
今天新增复制两个依赖到项目时,莫名其妙一个爆红artifactId和version,另一个爆红version,但放其他项目却正常,非常莫名其妙。经过一番折腾,终于发现不知道什么时候不小心多写了一个单独的导致的,但是这个异…...
【小白专用24.5.30已验证】Composer安装php框架thinkPHP6的安装教程
一、框架介绍 1、框架简介和版本选择 Thinkphp是一种基于php的开源web应用程序开发框架ThinkPHP框架,是免费开源的、轻量级的、简单快速且敏捷的php框架。你可以免费使用TP框架,甚至可以将你的项目商用; ThinkPHP8.0 是目前框架正式版的最新版…...
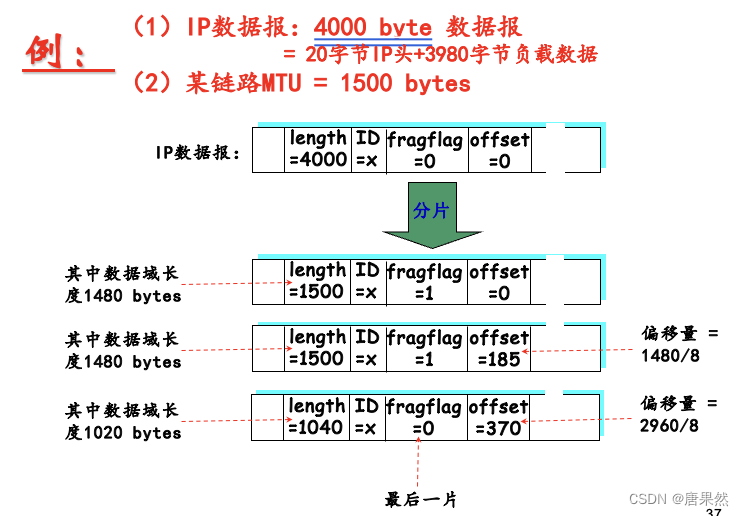
ch4网络层---计算机网络期末复习(持续更新中)
网络层概述 将分组从发送方主机传送到接收方主机 发送方将运输层数据段封装成分组 接收方将分组解封装后将数据段递交给运输层网络层协议存在于每台主机和路由器上 路由器检查所有经过它的IP分组的分组头 注意路由器只有3层(网络层、链路层、物理层) 网络层提供的服务 一…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
