Cholesky分解(A=L * L^T)
Cholesky分解是一种用于解线性方程组和计算矩阵平方根的算法,特别适用于对称正定矩阵。这种方法相比于其他解法(如高斯消元法)在数值稳定性上通常有更好的表现,并且能够有效地利用矩阵的对称性和正定性。下面简要介绍如何使用Cholesky分解求解线性方程组 Ax = b,其中A是对称正定矩阵。
Cholesky分解的步骤:
-
分解: 首先,将矩阵A进行Cholesky分解,即找到一个下三角矩阵L,使得 A = L ∗ L T A = L * L^T A=L∗LT。这个过程是通过逐行进行的,对于矩阵A的第k行和第k列元素,按照以下公式计算L的元素:
l k k = a k k − ∑ j = 1 k − 1 l k j 2 l_{kk} = \sqrt{a_{kk} - \sum_{j=1}^{k-1} l_{kj}^2} lkk=akk−j=1∑k−1lkj2
l i k = 1 l k k ( a i k − ∑ j = 1 k − 1 l i j l k j ) , i > k l_{ik} = \frac{1}{l_{kk}}(a_{ik} - \sum_{j=1}^{k-1} l_{ij}l_{kj}), \quad i > k lik=lkk1(aik−j=1∑k−1lijlkj),i>k
这样,就可以得到下三角矩阵L。
-
求解: 一旦得到了L,就可以通过两个步骤来解线性方程组 A x = b Ax=b Ax=b:
-
前向替换:首先解 L y = b Ly=b Ly=b,得到y。这可以通过以下递推式完成:
y 1 = b 1 l 11 y_1 = \frac{b_1}{l_{11}} y1=l11b1
y i = b i − ∑ j = 1 i − 1 l i j y j l i i , i = 2 , 3 , . . . , n y_i = \frac{b_i - \sum_{j=1}^{i-1} l_{ij}y_j}{l_{ii}}, \quad i = 2, 3, ..., n yi=liibi−∑j=1i−1lijyj,i=2,3,...,n -
后向替换:然后解 L T x = y L^Tx=y LTx=y,得到最终的解x。这一步是:
x n = y n x_n = y_n xn=yn
x i = y i − ∑ j = i + 1 n l j i x j , i = n − 1 , n − 2 , . . . , 1 x_i = y_i - \sum_{j=i+1}^{n} l_{ji}x_j, \quad i = n-1, n-2, ..., 1 xi=yi−j=i+1∑nljixj,i=n−1,n−2,...,1
-
示例代码(Python)
以下是一个简单的Python示例,使用NumPy库来实现Cholesky分解求解线性方程组:
import numpy as npdef cholesky_solve(A, b):# Cholesky分解L = np.linalg.cholesky(A)# 前向替换求yy = np.zeros_like(b)for i in range(len(b)):if i == 0:y[i] = b[i] / L[i, i]else:y[i] = (b[i] - np.dot(L[i, :i], y[:i])) / L[i, i]# 后向替换求xx = np.zeros_like(y)for i in reversed(range(len(b))):if i == len(b) - 1:x[i] = y[i]else:x[i] = y[i] - np.dot(L[i+1:, i], x[i+1:])return x# 示例矩阵A和向量b
A = np.array([[4, 12, -16], [12, 37, -43], [-16, -43, 98]])
b = np.array([1, 2, 3])# 求解
x = cholesky_solve(A, b)
print("解:", x)
请注意,上述代码直接实现了Cholesky分解和求解的过程,而在实际应用中,通常会直接使用像NumPy这样的库中的内置函数numpy.linalg.cholesky来完成分解,以及相关函数来简化求解过程。
相关文章:
)
Cholesky分解(A=L * L^T)
Cholesky分解是一种用于解线性方程组和计算矩阵平方根的算法,特别适用于对称正定矩阵。这种方法相比于其他解法(如高斯消元法)在数值稳定性上通常有更好的表现,并且能够有效地利用矩阵的对称性和正定性。下面简要介绍如何使用Chol…...

2024大模型新应用井喷即将到来,算力问题如何解决?
#大模型新应用 #NLP #智合同 随着人工智能技术的加速演进,AI大模型已成为全球科技竞争的新高地、未来产业的新赛道、经济发展的新引擎。大模型的快速发展,特别是在自然语言处理(NLP)和计算机视觉(CV)等…...

SpringBoot 七牛云 OSS 私有模式 获取访问链接
目录 一、问题引出 二、在SpringBoot中获取私有访问路径的操作 一、问题引出 由于七牛云OSS的公有模式存在被盗刷的风险,可能导致服务器额外的费用,于是我选择私有模式进行操作。私有模式的访问路径是一个问题,因为需要对应着token和e这两…...
python-模块-网络编程-多任务
一、模块 1-1 Python 自带模块 Json模块 处理json数据 {"key":"value"} json不是字典 本质是一个有引号的字符串数据 json注意点 {} 中的数据是字符串引号必须是双引号 使用json模块可以实现将json转为字典,使用字典的方法操作数据 。 或者将…...

火狐浏览器网页翻译
火狐浏览器网页翻译 火狐浏览器的翻译功能并不支持中文,无法将中文翻译成其他语言,也不支持将其他语言翻译成中文。如果需要翻译英文网页,可以安装翻译插件来帮助解决这个问题。 安装翻译插件的步骤如下: 打开火狐浏览器ÿ…...

R语言数据分析案例以及要点和难点
该案例将涵盖数据读取、数据清洗、探索性数据分析(EDA)、数据可视化和简单的统计分析等多个方面。本案例将以一家零售商店的销售数据为例,使用R语言进行数据分析。 1. 数据准备 假设我们有一个名为sales_data.csv的CSV文件,其中包含了零售商店的销售数据。该文件包含以下列…...

【STL源码剖析-空间配置器】stack、queue简单实现
举头天外望 无我这般人 目录 stack 的概述 stack 的实现 queue 的概述 queue 的实现 契子✨ 我们之前学过了 vector、list 这些 STL 的(容器) 而我们今天将要学习空间配置器 -- stack、queue,那什么是空间配置器呢? 简单来讲就是…...
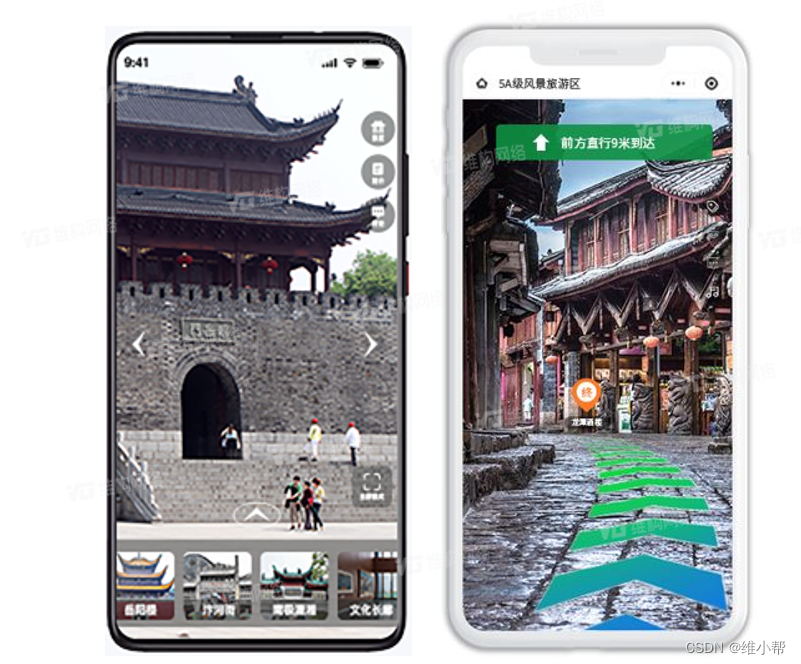
VR导航的实现原理、技术优势和应用场景
VR导航通过虚拟现实技术提供沉浸式环境,结合室内定位技术实现精准导航。目前,VR导航已在多个领域展现出其独特的价值和潜力,预示着智能导航系统的未来发展。 一、实现原理 VR导航技术依托于虚拟现实(VR)和室内定位系统。VR技术利用计算机模…...

淘宝镜像的https证书过期
错误原因: 淘宝镜像过期 早在 2021 年,淘宝就发文称,npm 淘宝镜像已经从 http://registry.npm.taobao.org 切换到了 http://registry.npmmirror.com。旧域名也将于 2022 年 5 月 31 日停止服务(直到 HTTPS 证书到期才真正不能用了…...

VSCODE 常用快捷键
快捷按键 注释 CTRL /CTRL KSHIFT ALT A取消注释 CTRL /CTRL KSHIFT ALT A搜索文件 Ctrl P移动到某一行 Ctrl g打开一个新窗口 Ctrl Shift N关闭窗口 Ctrl Shift W新建文件 Ctrl N文件间切换 Ctrl Tab全部文件搜索 Ctrl Shift F全屏 F11 打开文件出现中文乱码 文件右下角…...

医院该如何应对网络安全?
在线医生咨询受到很多人的关注,互联网医疗行业的未来发展空间巨大,但随着医院信息化建设高速发展 医院积累了大量的患者基本信息、化验结果、电子处方、生产数据和运营信息等数据 这些数据涉及公民隐私、医院运作和发展等多因素,医疗行业办…...

【qt】多窗口开发
多窗口开发 一.应用场景二.嵌入的窗口1.设计Widget窗口2.创建窗口3.添加窗口4.总代码 三.独立的窗口1.创建窗口2.显示窗口 四.总结 一.应用场景 多窗口,顾名思义,有多个窗口可以供我们进行操作! 截个小图,你应该就知道了 OK,话不多说,直接开干,先来设计我们的主窗口 需要蔬菜…...

iOS Hittest 机制和实际应用
Hittest 机制原理 hitTest的原理就是,当我们点击的时候,会触发 window的 hittest方法,在该方法中会首先使用point inside方法判断 点击的地方是否在window范围内,如果在的话,就倒序遍历姿子视图,然后将poi…...

C# 工厂模式学习
工厂模式(Factory Pattern)是一种创建型设计模式,它提供了一种创建对象的接口,而不是通过具体类来实例化对象。工厂模式可以将对象的创建过程封装起来,使代码更具有灵活性和可扩展性。 工厂模式有几种常见的实现方式&…...

AI生成微信职业头像
加油,新时代打工人! 真别说,还挺好看的 https://chatglm.cn/main/alltoolsdetail...

遥感图像的深度学习的任务类型
在遥感图像的深度学习任务中,利用深度学习技术处理和分析遥感图像已经成为一个重要的研究方向。遥感图像来自卫星、无人机等设备,包含了丰富的地球表面信息。以下是遥感图像深度学习中的主要任务类型: 1. 图像分类(Image Classif…...
162.二叉树:填充每个节点的下一个右侧节点指针(力扣)
代码解决 /* // Definition for a Node. class Node { public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _…...
--知识图谱+实体抽取)
NLP(20)--知识图谱+实体抽取
前言 仅记录学习过程,有问题欢迎讨论 基于LLM的垂直领域问答方案: 特点:不是通用语料;准确度要求高,召回率可以低(转人工);拓展性和可控性(改变特定内容的回答…...

【mysql数据库】mycat中间件
MyCat 简介 Mycat 是数据库 中间件 。 1、 数据库中间件 中间件 是一类连接软件组件和应用的计算机软件, 以便于软件各部件之间的沟通 。 例子 Tomcat web 中间件 。 数据库 中间件 连接 java 应用程序和数据库 2、 为什么要用 Mycat ① Java 与数据库紧耦合 …...

满帮集团 Eureka 和 ZooKeeper 的上云实践
作者:胡安祥 满帮集团,作为“互联网物流”的平台型企业,一端承接托运人运货需求,另一端对接货车司机,提升货运物流效率。2021 年美股上市,成为数字货运平台上市第一股。根据公司年报,2021 年&a…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
