sum-check protocol
sumcheck是一个交互式证明协议,给定域F上的多元多项式g(x1,...,xv)g(x_1,...,x_v)g(x1,...,xv),证明者Prover可以向验证者Verifier证明该多项式ggg的遍历求和值等于公开值HHH,即
H=∑b1,b2,...,bv∈{0,1}vg(b1,b2,...,bv)H= \sum_{b_1,b_2,...,b_v \in \{0,1\}^v}g(b_1,b_2,...,b_v) H=b1,b2,...,bv∈{0,1}v∑g(b1,b2,...,bv)
法一: Verifier可以直接通过上述等式计算验证,但直接计算需要2v2^v2v次求和
法二:Verifier将计算转移到计算能力更强的Prover,即本文所述的sum-check协议,通过sum-check协议,Prover使得Verifier相信其遍历求和值等于HHH
sumcheck
sumcheck一共需要进行vvv轮交互,其过程如下:
第1轮:
-
Prover:向Verifier发送一个单变量多项式( univariate polynomial)
g1(X1)=∑b2,...,bv∈0,1vg(X1,b2,...,bv)g_1(X_1)=\sum_{b_2,...,b_v \in{0,1}^v}g(X_1,b_2,...,b_v) g1(X1)=b2,...,bv∈0,1v∑g(X1,b2,...,bv) -
Verifier: 检查H=g1(0)+g1(1)H=g_1(0) + g_1(1)H=g1(0)+g1(1)是否成立,如果成立则随机选取r1∈Fr_1 \in Fr1∈F发送给Prover
第j轮:
-
Prover:向Verifier发送一个单变量多项式
gj(Xj)=∑bj+1,...,bv∈{0,1}vg(r1,...,rj−1,Xj,bj+1,...,bv)g_j(X_j)=\sum_{b_{j+1},...,b_v \in \{0,1\}^v}g(r_1,...,r_{j-1},X_j,b_{j+1},...,b_v) gj(Xj)=bj+1,...,bv∈{0,1}v∑g(r1,...,rj−1,Xj,bj+1,...,bv) -
Verifier: 检查gj−1(rj−1)=gj(0)+gj(1)g_{j-1}(r_{j-1})=g_j(0) + g_j(1)gj−1(rj−1)=gj(0)+gj(1)是否成立,如果成立则随机选取rj∈Fr_j \in Frj∈F发送给Prover
第v轮:
-
Prover:向Verifier发送一个单变量多项式
gv(Xv)=g(r1,r2...,rv−1,Xv)g_v(X_v)=g(r_1,r_2...,r_{v-1},Xv) gv(Xv)=g(r1,r2...,rv−1,Xv) -
Verifier: 检查gv−1(rv−1)=gv(0)+gv(1)g_{v-1}(r_{v-1})=g_v(0) + g_v(1)gv−1(rv−1)=gv(0)+gv(1)是否成立,如果成立则计算g(r1,r2,...,rv)g(r_1,r_2,...,r_v)g(r1,r2,...,rv) ,并验证g(r1,r2,...,rv)=gv(rv)g(r_1,r_2,...,r_v)= g_v(r_v)g(r1,r2,...,rv)=gv(rv)是否成立
例如 g(X1,X2,X3)=2X13+X1X3+X2X3g(X_1,X_2,X_3)= 2X_1^3 + X_1X_3+X_2X_3g(X1,X2,X3)=2X13+X1X3+X2X3 ,其遍历求和值H=12H =12H=12
第1轮:
-
Prover:向Verifier发送一个单变量多项式( univariate polynomial)
g1(X1)=8X13+2X1+1g_1(X_1)=8X_1^3+2X_1+1 g1(X1)=8X13+2X1+1 -
Verifier: 验证H=g1(0)+g1(1)=12H=g_1(0) + g_1(1) = 12H=g1(0)+g1(1)=12,并随机选取r1=2r_1 =2r1=2发送给Prover
第2轮:
-
Prover:向Verifier发送一个单变量多项式
g2(X2)=34+X2g_2(X_2)=34 + X_2 g2(X2)=34+X2 -
Verifier: 验证g1(2)=g2(0)+g2(1)=69g_{1}(2)=g_2(0) + g_2(1) = 69g1(2)=g2(0)+g2(1)=69,并随机选取r2=3r_2 =3r2=3发送给Prover
第3轮:
-
Prover:向Verifier发送一个单变量多项式
g3(X3)=16+5X3g_3(X_3)=16+5X_3 g3(X3)=16+5X3 -
Verifier: 验证g2(r2)=g3(0)+g3(1)=37g_{2}(r_{2})=g_3(0) + g_3(1)= 37g2(r2)=g3(0)+g3(1)=37,并随机选取r3=6r_3 =6r3=6,计算并验证g(r1,r2,...,rv)=46=g3(6)g(r_1,r_2,...,r_v) = 46 = g_3(6)g(r1,r2,...,rv)=46=g3(6)
相关文章:

sum-check protocol
sumcheck是一个交互式证明协议,给定域F上的多元多项式g(x1,...,xv)g(x_1,...,x_v)g(x1,...,xv),证明者Prover可以向验证者Verifier证明该多项式ggg的遍历求和值等于公开值HHH,即 H∑b1,b2,...,bv∈{0,1}vg(b1,b2,...,bv)H \sum_{b_1,b_2,…...
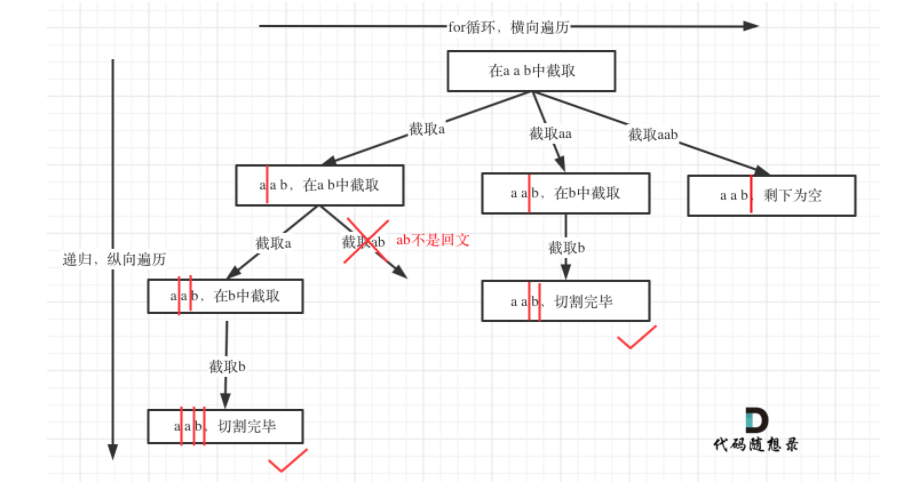
数据结构刷题(二十一):131分割回文串、78子集
1.分割回文串题目链接思路:回溯算法的组合方法(分割问题类似组合问题)。流程图:红色竖杠就是startIndex。 for循环是横向走,递归是纵向走。回溯三部曲:递归函数参数:字符串s和startIndex&#…...

Spring Aop 详解
主要内容: 了解Spring AOP的概念及其术语熟悉Spring AOP的JDK动态代理熟悉Spring AOP的CGLib动态代理掌握基于XML的AOP实现掌握基于注解的AOP实现AOP用官方话来说: AOP即面向切面编程。和OOP(面向对象编程)不同,AOP主…...

【数据库死锁】线上问题之数据库死锁
原本平静的一天,惊现生产项目瘫痪问题,马上打开日志,发现后台日志提示了多个“com.mysql.cj.jdbc.exceptions.MySQLTransactionRollbackException: Lock wait timeout exceeded; try restarting transaction” 大概去了解一下这个异常&#x…...

好友管理系统--课后程序(Python程序开发案例教程-黑马程序员编著-第4章-课后作业)
实例3:好友管理系统 如今的社交软件层出不穷,虽然功能千变万化,但都具有好友管理系统的基本功能,包括添加好友、删除好友、备注好友、展示好友等。下面是一个简单的好友管理系统的功能菜单,如图1所示。 图1 好友管理系…...

Redis 集群 Redis Cluster搭建
Redis集群需要至少三个master节点,我们这里搭建三个master节点192.168.20.130,192.168.20.131,192.168.20.132,并且给每个master再搭建一个slave节点(一个节点一主一从,通过端口号区分)…...
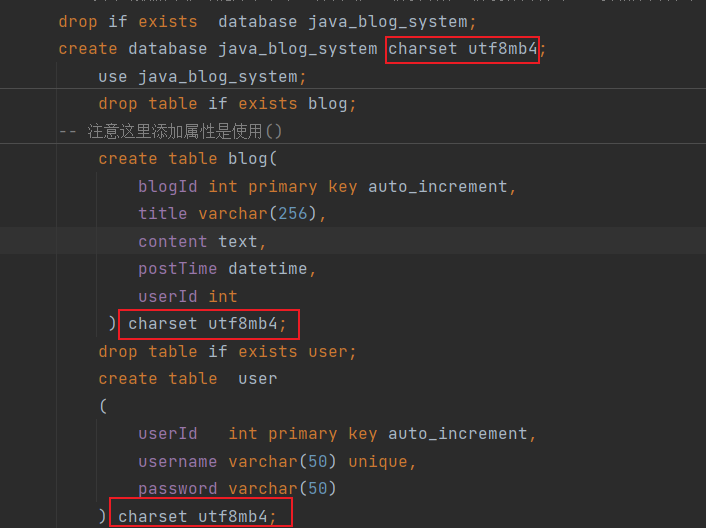
博客系统(前后端分离版)
博客系统的具体实现 文章目录博客系统的具体实现软件开发的基本流程具体实现的八大功能数据库设计创建数据库操作数据库引入依赖封装DataSource创建实体类将JDBC增删改查封装起来实现博客列表页web.xml的配置文件实现博客系统的展示功能登录功能强制要求用户登录显示用户信息退…...
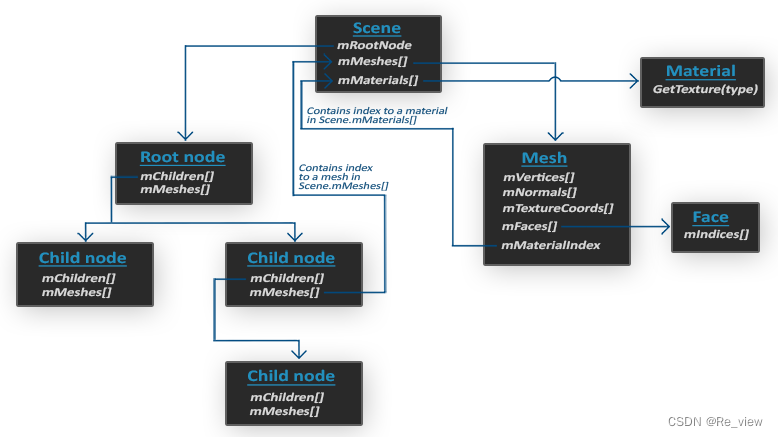
第十二章 opengl之模型加载(Assimp)
OpenGLAssimp模型加载库构建Assimp网格网格渲染Assimp 我们不太能够对像是房子、汽车或者人形角色这样的复杂形状手工定义所有的顶点、法线和纹理坐标。我们要的是将这些模型(Model)导入(Import)到程序当中。模型通常都由3D艺术家在Blender、3DS Max或者Maya这样的工具中精心制…...

Stable Matching-稳定匹配问题【G-S算法,c++】
Stable Matching-稳定匹配问题【G-S算法,c】题目描述:(Gale-Shapley算法)解题思路一:G-S算法(Gale-Shapley算法)题目描述:(Gale-Shapley算法) Teenagers from the local high school have asked you to help them with the organ…...
TypeScript(四)接口
目录 前言 定义 用法 基本用法 约定规则 属性控制 任意属性 可选属性 只读属性 定义函数 冒号定义 箭头定义 接口类型 函数接口 索引接口 继承接口 类接口 总结 前言 在介绍TS对象类型中,为了让数组每一项更具体,我们使用 string [ ]…...

Python-基础知识
目录 Python 简介 Python 发展历史 Python 特点 Python 标识符 Python 保留字符 行和缩进 多行语句 Python 引号 Python注释 Python 简介 Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python 的设计具有很强的可读性,相比…...
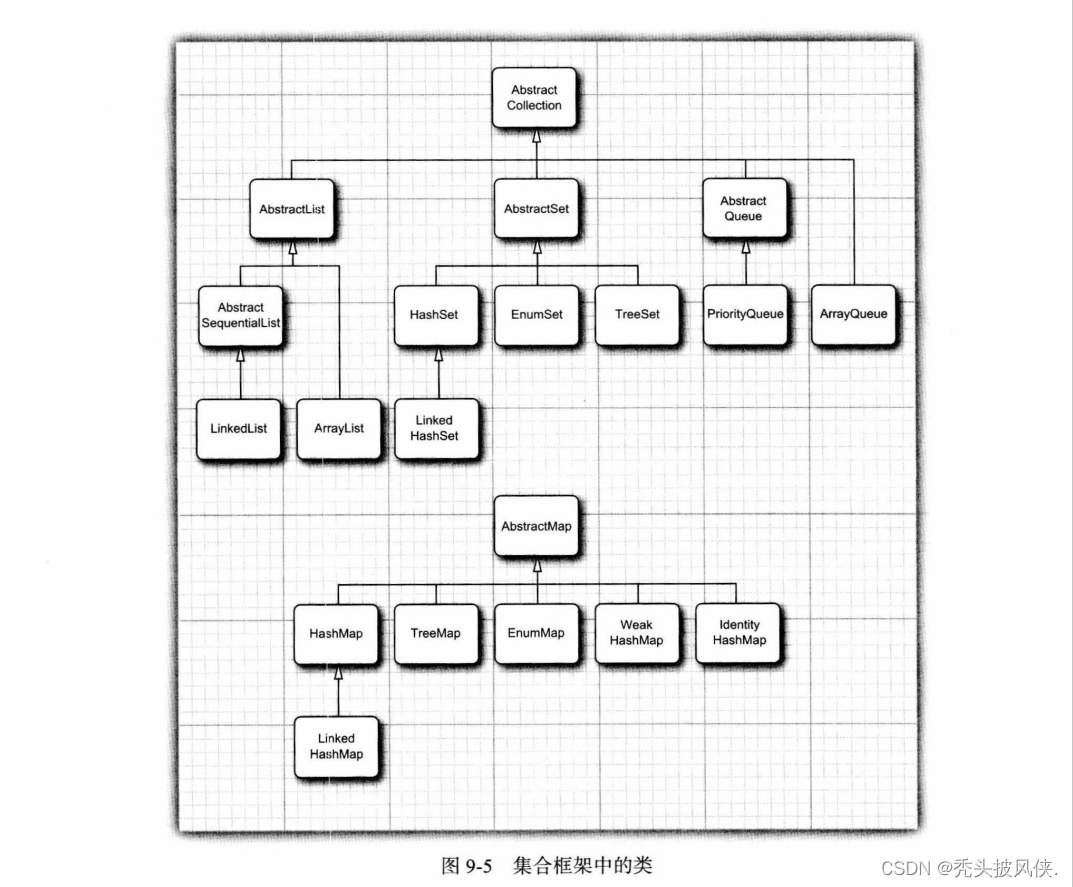
【java基础】集合基础说明
文章目录基本介绍Collection接口Iterator和Iterable接口Map接口关于Iterator接口的一些说明框架中的接口具体集合总结基本介绍 集合就是存储用来存储一系列数据的一种数据结构。在这篇文章中会介绍集合的一些基本概念。 Collection接口 集合的基本接口是Collection接口&…...
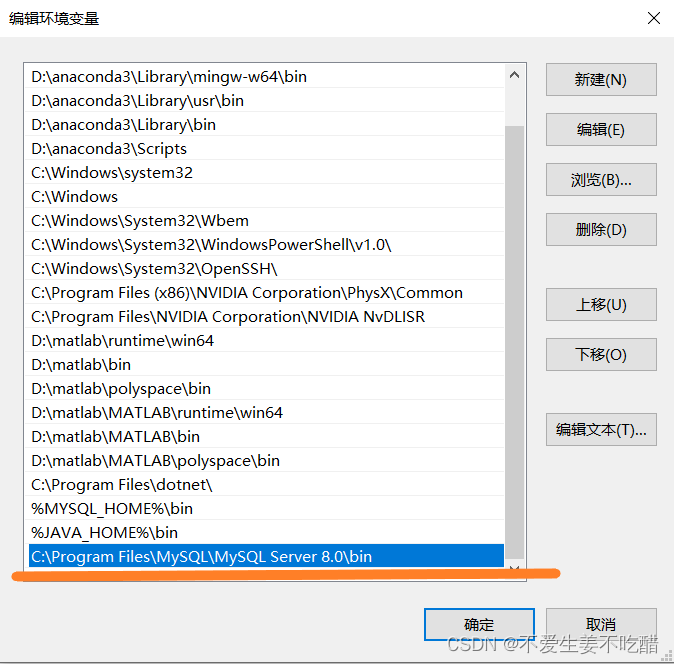
MySQL的下载及安装详细教程
提示:本文仅为MySQL初学者的安装MySQL过程提供参考,创作不易,请多点赞支持! MySQL的下载及安装前言一、MySQL的下载及安装1.MySQL的下载2.MySQL的安装3.配置环境变量4.连接MySQL4.1 方式一4.2 方式二前言 本文内容主要是帮助初学…...

SSL/TLS协议工作原理
SSL/TLS协议工作原理 SLL/TLS协议工作在应用层和传输层之间,应用层数据需要经过SSL/TLS层的加密之后才会发送到传输层。SSL/TLS协议有两个重要协议:握手协议、记录协议。 1. 握手协议 TCP三次握手完成后,才能进行SSL/TLS的握手。 因为&#…...

大数据项目实战之数据仓库:用户行为采集平台——第4章 用户行为数据采集模块
第4章 用户行为数据采集模块 4.1 数据通道 4.2 环境准备 4.2.1 集群所有进程查看脚本 1)在/home/atguigu/bin目录下创建脚本xcall [atguiguhadoop102 bin]$ vim xcall2)在脚本中编写如下内容 #! /bin/bashfor i in hadoop102 hadoop103 hadoop104 d…...
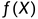
《统计学习方法》(李航)——学习笔记
第一章 概论统计学习,又称统计机器学习(机器学习),现在提到的 机器学习 往往指的就是 统计机器学习。统计学习研究的对象是数据,其对数据的基本假设是同类数据存在一定的统计规律性,因此可以用概率统计方法…...
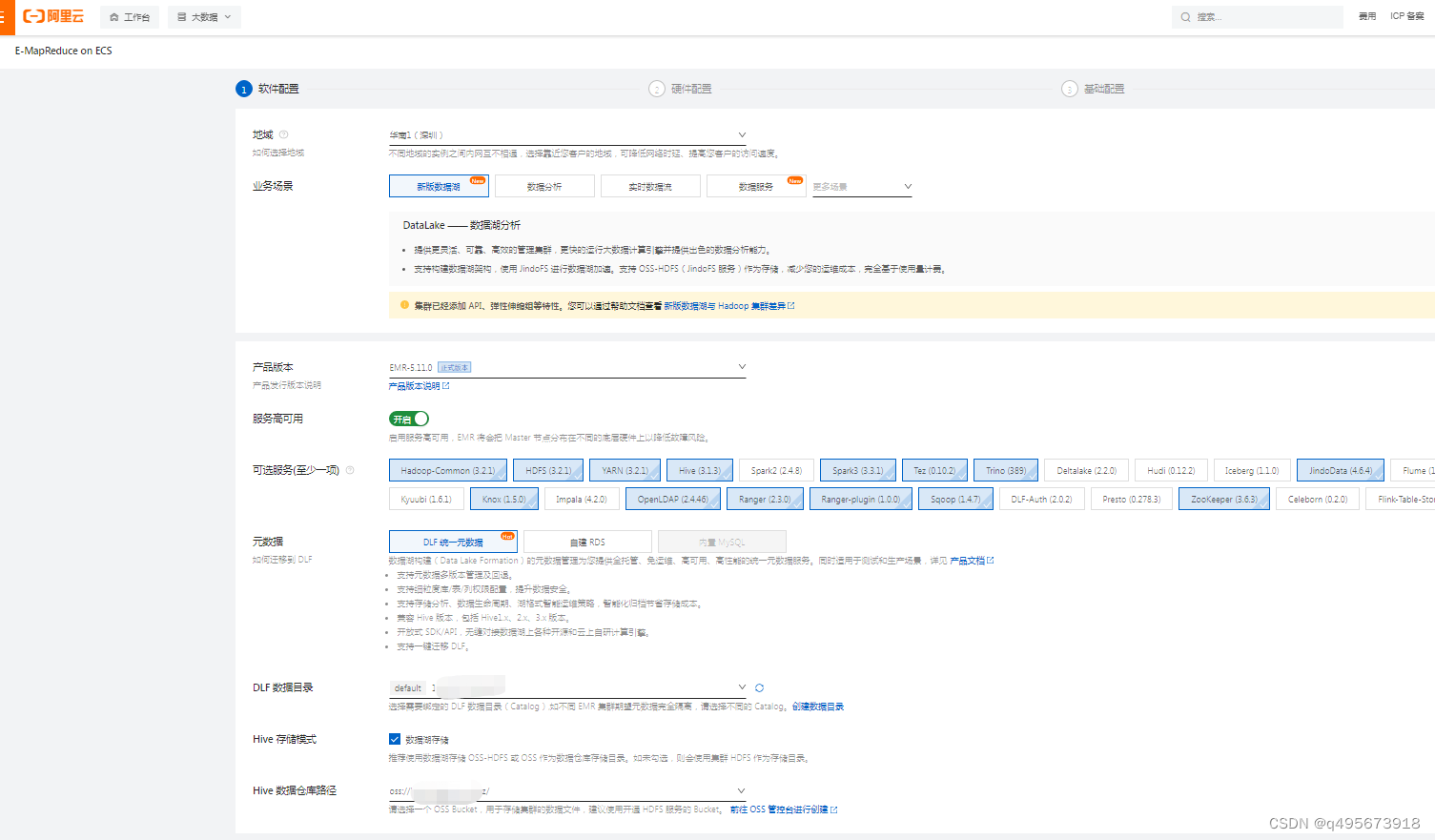
阿里云EMR集群搭建及使用
目录 1.简介 1.什么是EMR 2.组成 3.与自建hadoop集群对比 4.产品架构 2.使用 1.创建EMR集群 1.登录EMR on ECS控制台 2.软件设置 3.硬件设置 3.基础配置 2.配置 1.组件配置 2.用户管理 3.安全组 4.Gateway 3.组件UI 1.简介 1.什么是EMR EMR是运行在阿里云平台…...

学习streamlit-4
st.slider 今天学习st.slider滑块组件的使用。 st.slider滑块组件通常被用来作为应用的输入,支持整数、浮点数、日期、时间和日期时间。 下面的示例程序包含以下简单功能,以演示st.slider滑块组件: 用户通过调整滑块选择值应用打印出所选…...

高级Oracle DBA面试题及答案
作为高级 Oracle DBA,您将负责 Oracle 数据库基础架构的设计、安装、配置、监控和维护。您还将负责制定和实施备份和恢复计划,并确保数据的安全性和完整性。要成功担任此职位,您需要对 Oracle 数据库架构有深入的了解,并能够有效地…...

程序员成长路线
程序员在成长的过程中,不同的阶段,需要关注的问题点一会都会有所不同,今天给大家分享下自己的感受。 0-1年,入门,掌握语言基础、提高工具的使用熟练度。 工作第一年,主要围绕ssm三件套、mysql、red…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
