为什么要保持方差为1
1.数值稳定性: 在机器学习和深度学习中,维持激活函数输入的方差在一个合理范围内(如1)是很重要的,这有助于防止在训练过程中发生梯度消失或梯度爆炸的问题。如果方差过大或过小,经过多层网络后输出结果的方差可能变得极大或极小,这会影响梯度的有效传递,从而影响模型学习。
2.梯度的有效传播: 保持输入方差约为1有助于保持整个网络中的信息和梯度流的稳定性。这是因为当数据经过多个处理层时,未缩放的变量可能会导致变化幅度过大或过小,从而导致训练过程不稳定。【也就是数值不稳定,经过多层网络后方差可能变为极大或者极小,影响模型学习】
3.举个例子(分为方差为1,方差过大,方差过小三种情况)
1、方差为1
输入层:输入数据的方差为1,这意味着数据在0周围分布得比较均匀,没有极端的大值或小值。
第一层:这层的权重初始化为使得输出方差保持为1。因此,当输入数据通过激活函数(如ReLU或Sigmoid)传递时,输出数据的方差仍为1。
第二层和更多层:由于输入方差保持不变,每层都可以在不调整学习率的情况下有效地学习,梯度也不会消失或爆炸。
LSTM的学习(包括sigmoid梯度消失原因解析)
2、方差过大
输入层:假设输入数据的方差非常大。
第一层:输入数据的方差大导致了神经元输出的方差也很大。这可能会导致激活函数(尤其是像Sigmoid或Tanh这样的函数)饱和,导致梯度几乎为零(梯度消失),接下来可能参数并未更新到理想状态(陷入局部极小值情况),但是梯度消失更新不动了。
第二层和更多层:因为梯度消失,网络在这些层的学习效率极低,难以对数据特征做出正确的反应和调整。
3、方差过小
输入层:输入数据的方差非常小。
第一层:小的方差意味着输出的变化幅度很小,这可能导致输出对输入的变化不敏感,同样可能导致梯度非常小。
第二层和更多层:小的梯度导致网络学习非常缓慢,甚至几乎不更新权重,难以达到良好的训练效果。
相关文章:

为什么要保持方差为1
1.数值稳定性: 在机器学习和深度学习中,维持激活函数输入的方差在一个合理范围内(如1)是很重要的,这有助于防止在训练过程中发生梯度消失或梯度爆炸的问题。如果方差过大或过小,经过多层网络后输出结果的方…...

Wpf 使用 Prism 实战开发Day31
登录数据绑定 1.首先在LoginViewModel 登录逻辑处理类中,创建登录要绑定属性和命令 public class LoginViewModel : BindableBase, IDialogAware {public LoginViewModel(){ExecuteCommand new DelegateCommand<string>(Execure);}public string Title { ge…...

Linux权限提升二
#应用场景: 获取到Web权限或普通用户在Linux服务器上时进行的SUID&SUDO提权 SUID (Set owner User ID up on execution)是给予文件的一个特殊类型的文件权限。在Linux/Unix中,当一个程序运行的时候,程序将从登录用户处继承权限。SUID被定…...
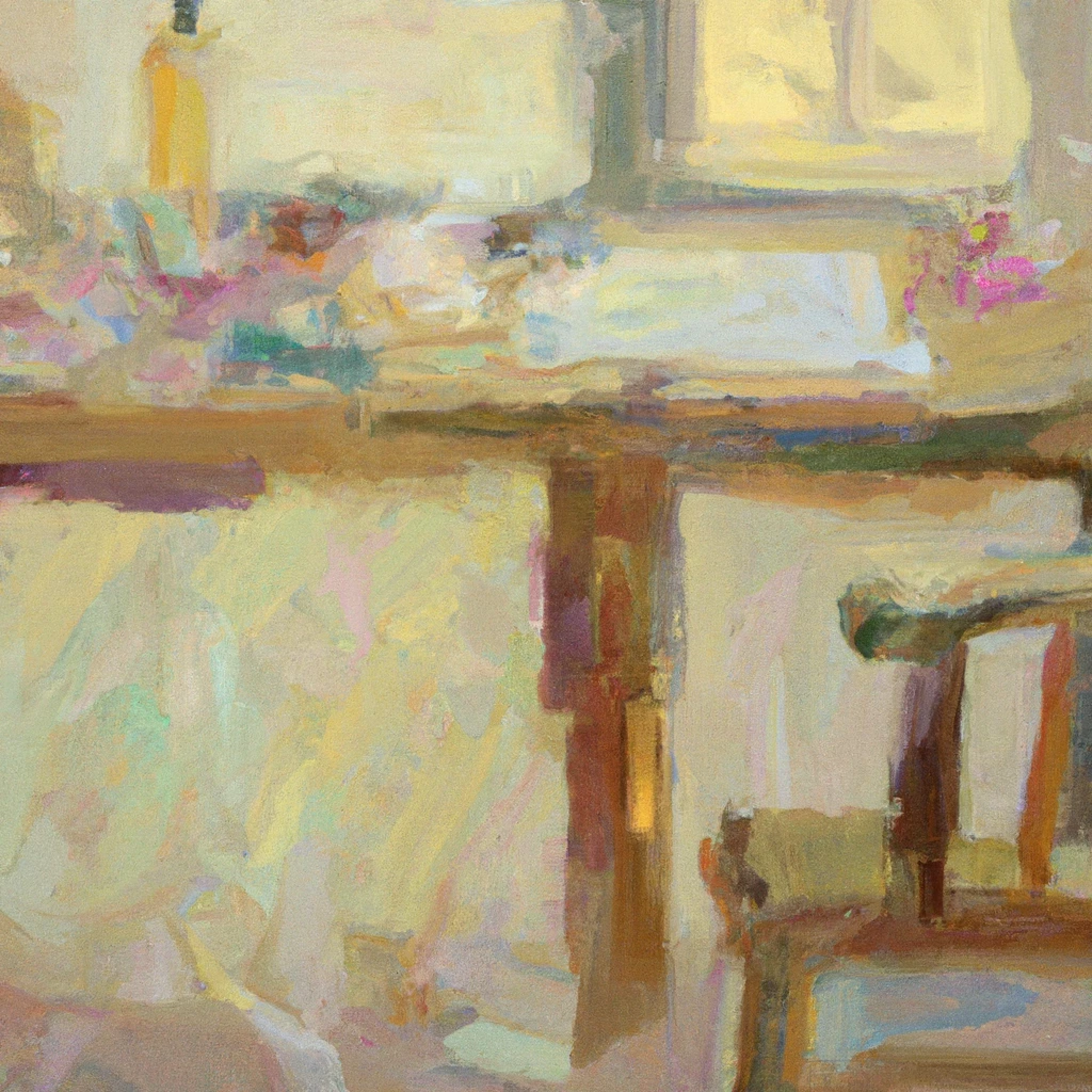
[AI OpenAI] 推出ChatGPT Edu
一种负担得起的解决方案,帮助大学将AI负责任地引入校园。 我们宣布推出ChatGPT Edu,这是一个专为大学设计的ChatGPT版本,旨在负责任地向学生、教职员工、研究人员和校园运营部署AI。ChatGPT Edu由GPT-4o提供支持,能够跨文本和视觉…...

HTML5+CSS3回顾总结
一、HTML5新特性 1.语义化标签 <header> 头部标签<nav> 导航标签<article> 内容标签<section> 定义文档某个区域<aside> 侧边栏标签<footer> 尾部标签 2.多媒体标签 2.1视频标签vedio 》常规写法(尽量都使用mp4࿰…...
:2024.05.01-2024.05.10)
AI推介-多模态视觉语言模型VLMs论文速览(arXiv方向):2024.05.01-2024.05.10
文章目录~ 1.Pseudo-Prompt Generating in Pre-trained Vision-Language Models for Multi-Label Medical Image Classification2.VLSM-Adapter: Finetuning Vision-Language Segmentation Efficiently with Lightweight Blocks3.Memory-Space Visual Prompting for Efficient …...
)
Python 点云生成高程模型图(DSM)
点云生成高程模型图 一、什么是DSM?二、python代码三、结果可视化一、什么是DSM? DSM(Digital Surface Model)是一种数字高程模型,通常用于描述地表地形的数字化表示。它是由一系列离散的高程数据点组成的三维地形模型,其中每个点都具有其相应的高程值。 DSM主要用于…...
[第五空间 2021]WebFTP
题目是WebFTP 通过标签可以看出git泄露(git泄露是指开发人员利用git进行版本控制) 通过网上了解WebFTP的源码账号admin 密码admin888 进去之后正常思路是我们利用/.git 在githack里面进行复现 查看log看看有没有flag 但是经过我们查询之后不是这样子 通过一段时间摸索在phpinf…...
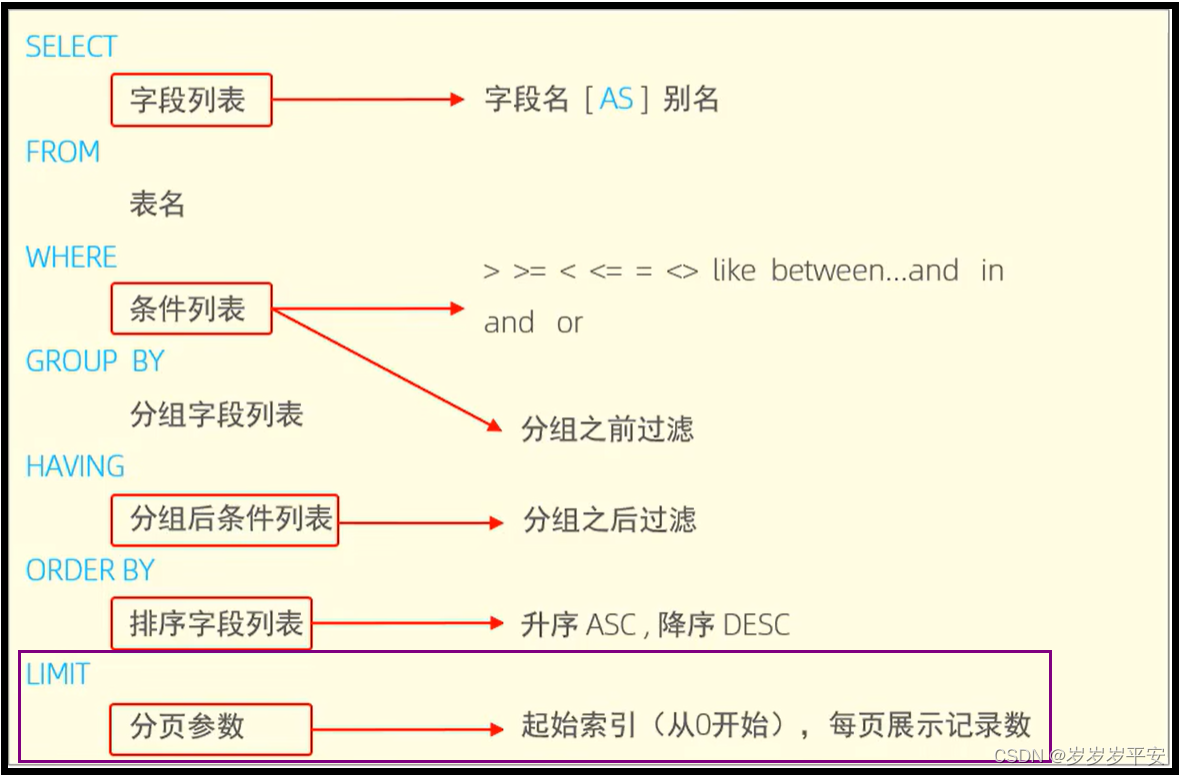
SQL—DQL(数据查询语言)之小结
一、引言 在前面我们已经学习完了所有的关于DQL(数据查询语言)的基础语法块部分,现在对DQL语句所涉及的语法,以及需要注意的事项做一个简单的总结。 二、DQL语句 1、基础查询 注意: 基础查询的语法是:SELE…...
找回xmind文件办法:一切意外均可找回(误删/重启关机等)
我周三编辑完,周四下午评审完用例忘记保存 结果到了快乐星期五,由于是周五我太开心了...早上到公司后觉得电脑卡,直接点了重启啥都没保存啊啊啊啊啊 准备上传测试用例时才想起来我的用例找不见了!!!&…...
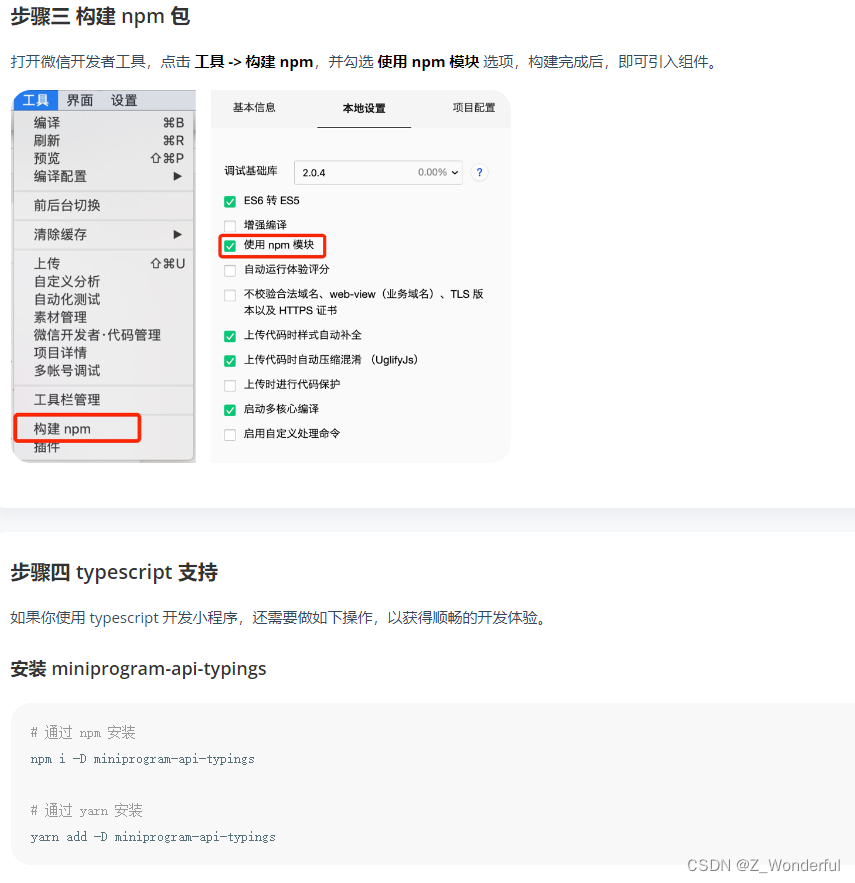
微信小程序 npm构建+vant-weaap安装
微信小程序:工具-npm构建 报错 解决: 1、新建miniprogram文件后,直接进入到miniprogram目录,再次执行下面两个命令,然后再构建npm成功 npm init -y npm install express(Node js后端Express开发ÿ…...

【LeetCode 63】 不同路径 II
1. 题目 2. 分析 这道题比较典型,跟最小路径和 是同样的思想。比较简单。 3. 代码 class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:row len(obstacleGrid)col len(obstacleGrid[-1]) dp [[0] *(col) f…...
OpenAI助手API接入-问答对自动生成
支持GPT-3.5-Turbo, GPT-4o, GPT-4-Turbo import json import openai from pathlib import Path import os client openai.OpenAI(base_urlbase_url, api_keyapi_key) file client.files.create( fileopen("H3.pdf", "rb"), purposeassistants ) …...
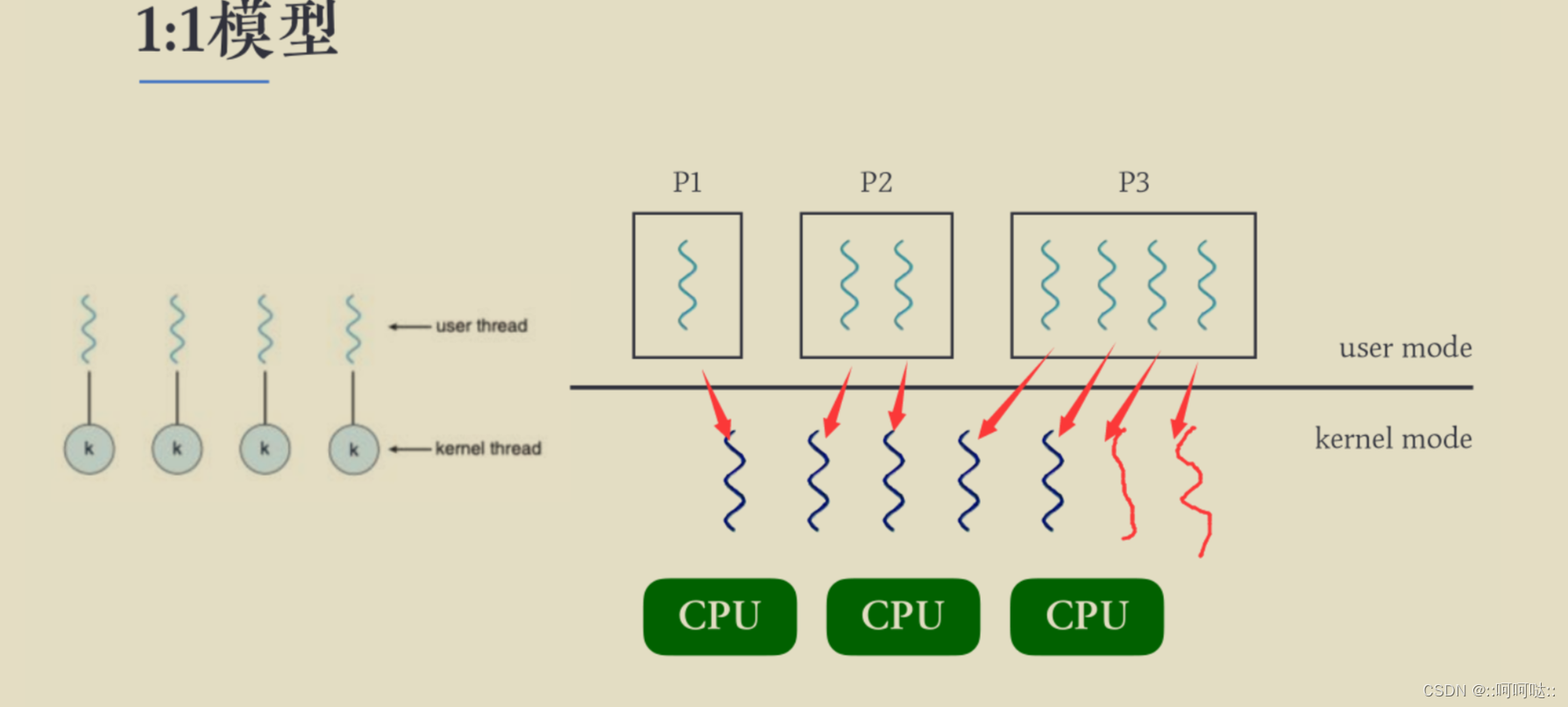
9. C++通过epoll+fork的方式实现高性能网络服务器
epollfork 实现高性能网络服务器 一般在服务器上,CPU是多核的,上述epoll实现方式只使用了其中的一个核,造成了资源的大量浪费。因此我们可以将epoll和fork结合来实现更高性能的网络服务器。 创建子进程函数–fork( ) 要了解线程我们先来了解…...

【Mac】XMind for mac(XMind思维导图)v24.04.10311软件介绍和安装教程
软件介绍 XMind for Mac是一款功能强大的思维导图软件。它具有以下主要特点: 1.多样化的思维导图功能:XMind for Mac提供了丰富的思维导图编辑功能,用户可以创建各种类型的思维导图,包括组织结构图、逻辑图、时间轴图等…...

使用 Django ORM 进行数据库操作
文章目录 创建Django项目和应用定义模型查询数据更新和删除数据总结与进阶聚合和注解跨模型查询原始SQL查询 Django是一个流行的Web应用程序框架,它提供了一个强大且易于使用的对象关系映射(ORM)工具,用于与数据库进行交互。在本文…...
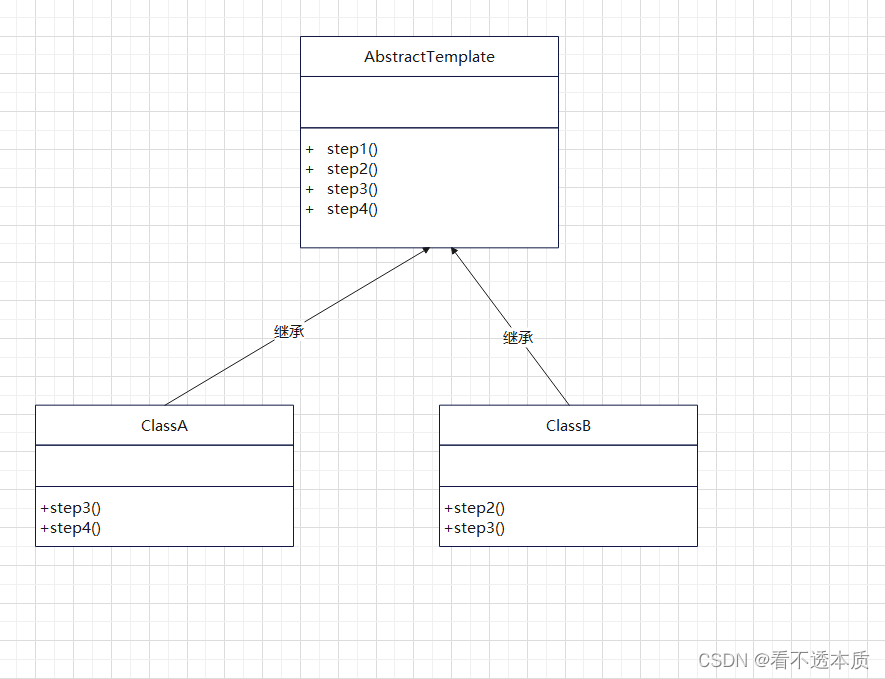
行为型设计模式之模板模式
文章目录 概述原理结构图实现 小结 概述 模板方法模式(template method pattern)原始定义是:在操作中定义算法的框架,将一些步骤推迟到子类中。模板方法让子类在不改变算法结构的情况下重新定义算法的某些步骤。 模板方法中的算法可以理解为广义上的业…...

大泽动力车载柴油发电机的特点和优势有哪些
大泽动力车载柴油发电机具有一系列显著的特点和优势,以下是对其的详细介绍: 低噪音性能:大泽动力车载柴油发电机具备明显的低噪音性能,其噪音限值在距离机组7米处测得为70dB(A),这为用户提供了一个相对安静的工作环境…...
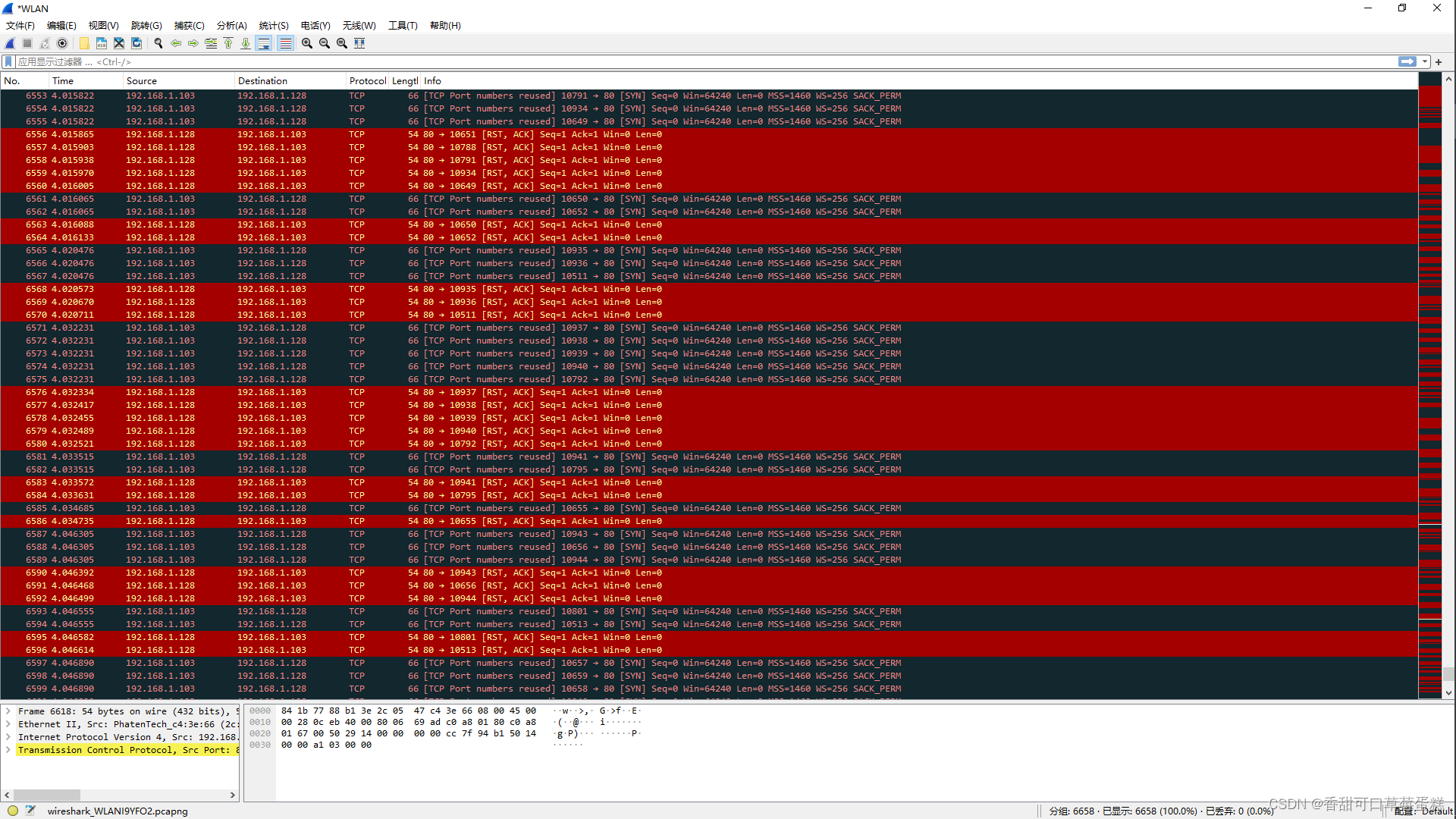
基于 IP 的 DDOS 攻击实验
一、介绍 基于IP的分布式拒绝服务(Distributed Denial of Service, DDoS)攻击是一种利用大量受控设备(通常是僵尸网络)向目标系统发送大量请求或数据包,以耗尽目标系统的资源,导致其无法正常提供服务的攻击…...

GPT-4o如何重塑AI未来!
如何评价GPT-4o? 简介:最近,GPT-4o横空出世。对GPT-4o这一人工智能技术进行评价,包括版本间的对比分析、GPT-4o的技术能力以及个人感受等。 GPT-4o似乎是一个针对GPT-4模型进行优化的版本,它在性能、准确性、资源效率以及安全和…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
