练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw.
第10题:在10维列向量构成的内积空间 V V V中,定义由向量 v v v引起的反射为 P v ( x ) = x − 2 ( x , v ) ( v , v ) v . P_v(x)=x-2\frac{(x,v)}{(v,v)}v. Pv(x)=x−2(v,v)(x,v)v. 今有向量 v , w ∈ V v, w\in V v,w∈V, 满足 0 < ( v , w ) < ( v , v ) ( w , w ) . 0< (v,w)<\sqrt{(v,v)\, (w,w)}. 0<(v,w)<(v,v)(w,w). 记 Q = P w ∘ P v Q=P_w \circ P_v Q=Pw∘Pv. 则所有满足 P ∘ Q = Q ∘ P P \circ Q = Q \circ P P∘Q=Q∘P的线性变换 P : V → V P: V \to V P:V→V构成的子空间的维数是多少?
解:依题意,向量 v , w v, w v,w线性无关. 不妨假设 v , w v, w v,w夹角为 θ / 2 ∈ ( 0 , π / 2 ) \theta/2 \in (0, \pi/2) θ/2∈(0,π/2) (注意 P v = P − v P_v = P_{-v} Pv=P−v. 必要时用 − v -v −v代替 v v v,即可保证夹角为锐角). 在二维子空间 W = s p a n ( v , w ) W=\mathrm{span}(v, w) W=span(v,w)中,线性变换 Q Q Q的效果是逆时针旋转 θ \theta θ. 熟知这可以用旋转矩阵 R θ = ( c − s s c ) R_\theta = \begin{pmatrix} c & -s \\ s & c \end{pmatrix} Rθ=(cs−sc)给出,其中 c = cos θ , s = sin θ c=\cos \theta,\; s= \sin \theta c=cosθ,s=sinθ. 而全部与 R θ R_\theta Rθ 乘法可交换的矩阵都是像 A a , b = ( a − b b a ) A_{a, b}=\begin{pmatrix} a & -b \\ b & a \end{pmatrix} Aa,b=(ab−ba)的形式。这些矩阵在全部2阶矩阵构成的线性空间中,组成了一个2维子空间。
在 V V V中, W W W的正交补 W ⊥ W^\perp W⊥是 8 8 8维的。在 W ⊥ W^\perp W⊥中进行任何的线性变换,都与 Q Q Q乘法可交换。所以所求的线性子空间维数是 8 × 8 + 2 = 66 8\times 8 + 2=66 8×8+2=66维。
注意:如果把10维改为一般的 n ( ≥ 2 ) n (\geq 2) n(≥2)维,那么答案是 ( n − 2 ) 2 + 2 (n-2)^2 + 2 (n−2)2+2维.
第11题: 10 10 10阶矩阵 A A A满足每行恰有 5 5 5个 1 1 1 和 5 5 5 个 0 0 0,且使得 A 2 + 5 A A^2+5A A2+5A是一个全部元素均为 5 5 5的矩阵. 问这样的矩阵 A A A有多少个?
解:(1) A A A的对角元不能是 1 1 1, 所以只能是 0 0 0. 这是因为如果 A A A有一个对角元是 1 1 1, A 2 + 5 A A^2+5A A2+5A相应的对角元就至少是 6 6 6.
(2) 用 J 2 n J_{2n} J2n表示元素全部是 1 1 1的 2 n 2n 2n阶方阵。从 A 2 + 5 A = 5 J 10 A^2+5A=5J_{10} A2+5A=5J10可知,如果 A A A的第 ( i , j ) (i,j) (i,j)位置是 1 1 1, 则 A 2 A^2 A2的第 ( i , j ) (i,j) (i,j)位置是 0 0 0; 如果 A A A的第 ( i , j ) (i, j) (i,j)位置是 0 0 0, 则 A 2 A^2 A2的第 ( i , j ) (i, j) (i,j)位置是 5 5 5. 由此可知, A A A的第 k k k列中 1 1 1的位置与 A A A的第 k k k行中 1 1 1的位置相同,所以 A A A是对称矩阵。
(3)从等式 A 2 + 5 A = 5 J 10 A^2+5A=5J_{10} A2+5A=5J10以及 A = A ⊤ A=A^\top A=A⊤可见,只要 A A A的第一行确定了,那么 A 2 A^2 A2的第一行, A A A的第一列也就确定了,从而 A A A的其它行也随之确定.
所以,只要 A A A的第一行确定了, A A A就被确定了。想要确定 A A A的第一行,只需要把 5 5 5个 1 1 1放到非对角线的位置(共 9 9 9个位置可选)。这等价于说把剩下的 4 4 4个 0 0 0放到第一行剩下的 9 9 9个位置。所以不同的 A A A共有 ( 9 5 ) = ( 9 4 ) = 126 \binom{9}{5}=\binom{9}{4}=126 (59)=(49)=126个.
注意:如果题目条件改为“ 2 n 2n 2n阶方阵 A A A满足 A 2 + n A = n J 2 n A^2+nA=nJ_{2n} A2+nA=nJ2n, 且 A A A的每行恰有 n n n个 0 0 0与 n n n个 1 1 1”. 则这样的方阵共有 ( 2 n − 1 n ) = ( 2 n − 1 n − 1 ) \binom{2n-1}{n}=\binom{2n-1}{n-1} (n2n−1)=(n−12n−1)个.
相关文章:

练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw. 第10题:在10维列向量构成的内积空间 V V V中…...

乐高小人分类项目
数据来源 LEGO Minifigures | Kaggle 建立文件目录 BASE_DIR lego/star-wars-images/ names [YODA, LUKE SKYWALKER, R2-D2, MACE WINDU, GENERAL GRIEVOUS ] tf.random.set_seed(1)# Read information about dataset if not os.path.isdir(BASE_DIR train/):for name in …...

个人关于ChatGPT的用法及建议
概述 这里只是个人常用的几个软件,做一下汇总,希望对各位有用。 如果有更高认知的朋友,请留下你的工具名称,提醒我一下,谢谢~ 常用的chatgpt模型工具: 以下是一些知名的例子: 文…...

神经网络的工程基础(二)——随机梯度下降法|文末送书
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 本文涉及到的代码链接如下:regression2chatgpt/ch06_optimizer/stochastic_gradient_descent.ipynb 本文将讨论利用…...

常见的几种编码方式
常见的编码方式及其特点: 编码方式的设计是为了适应不同的字符集和应用需求,因此它们在表示字符时使用的位数和字节数各不相同 常见编码方式及其位数和字节数 ASCII(American Standard Code for Information Interchange)&#x…...
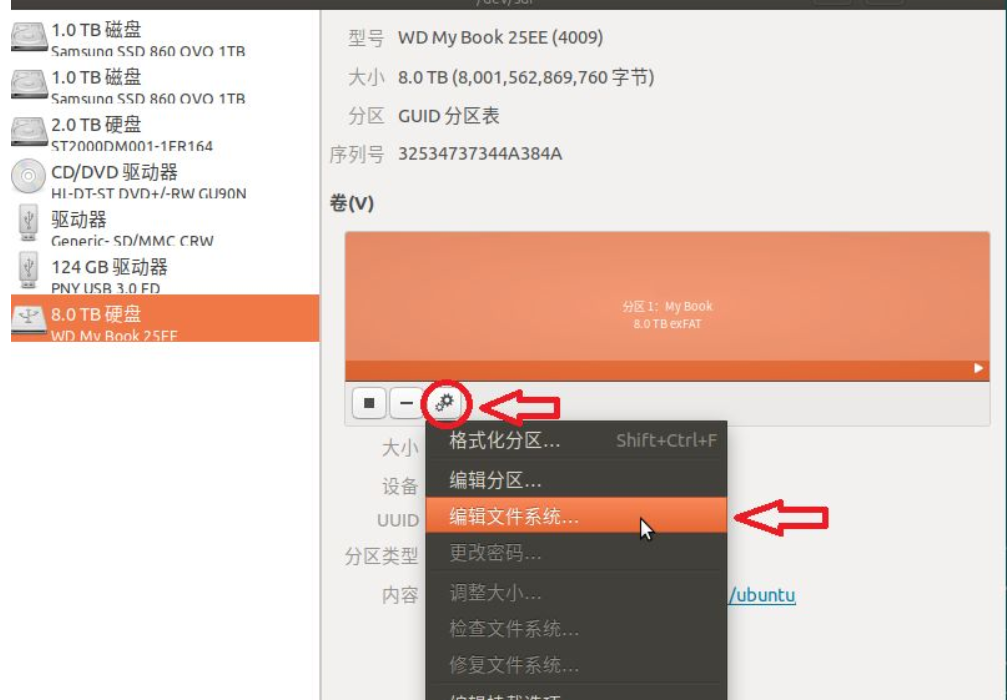
ubuntu移动硬盘重命名
因为在ubuntu上移动硬盘的名字是中文的,所以想要改成英文的。 我的方法: 将移动硬盘插到windows上,直接右键重命名。再插到ubuntu上名字就改变了。 别人的方法: ubuntu下如何修改U盘名字-腾讯云开发者社区-腾讯云 在自带的软件…...

VUE框架前置知识总结
一、前言 在学习vue框架中,总是有些知识不是很熟悉,又不想系统的学习JS,因为学习成本太大了,所以用到什么知识就学习什么知识。此文档就用于记录零散的知识点。主要是还是针对与ES6规范的JS知识点。 以下实验环境都是在windows环…...

张宇1000题80%不会?别急,这个方法肯定有用!
这太正常了,1000题的难度本来就高,不要慌 我考研的时候跟的也是张宇老师,但是1000题我根本就没做几道题就给换成880题660题了,而且只是强化阶段用880题,基础阶段我用的都是汤家凤的1800题。 不要担心做的不是张宇老师…...

【python】爬虫记录每小时金价
数据来源: https://www.cngold.org/img_date/ 因为这个网站是数据随时变动的,用requests、BeautifulSoup的方式解析html的话,数据的位置显示的是“--”,并不能取到数据。 所以采用webdriver访问网站,然后从界面上获取…...
一行命令将已克隆的本地Git仓库推送到内网服务器
一、需求背景 我们公司用gitea搭建了一个git服务器,其中支持win7的最高版本是v1.20.6。 我们公司的电脑在任何时候都不能连接外网,但是希望将一些开源的仓库移植到内网的服务器来。一是有相关代码使用的需求,二是可以建设一个内网能够查阅的…...

Linux文本处理三剑客(详解)
一、文本三剑客是什么? 1. 对于接触过Linux操作系统的人来说,应该都听过说Linux中的文本三剑客吧,即awk、grep、sed,也是必须要掌握的Linux命令之一,三者都是用来处理文本的,但侧重点各不相同,a…...
AI在线UI代码生成,不需要敲一行代码,聊聊天,上传图片,就能生成前端页面的开发神器
ioDraw的在线UI代码生成器是一款开发神器,它可以让您在无需编写一行代码的情况下创建前端页面。 主要优势: 1、极简操作:只需聊天或上传图片,即可生成响应式的Tailwind CSS代码。 2、节省时间:自动生成代码可以节省大…...

go-zero整合单机版ClickHouse并实现增删改查
go-zero整合单机版ClickHouse并实现增删改查 本教程基于go-zero微服务入门教程,项目工程结构同上一个教程。 本教程主要实现go-zero框架整合单机版ClickHouse,并暴露接口实现对ClickHouse数据的增删改查。 go-zero微服务入门教程:https://b…...
行政工作如何提高效率?桌面备忘录便签软件哪个好
在行政管理工作中,效率的提高无疑是每个行政人员都追求的目标。而随着科技的发展,各种便捷的工具也应运而生,其中桌面备忘录便签软件便是其中的佼佼者。那么,这类软件又如何帮助我们提高工作效率呢? 首先,…...

利用向日葵和微信/腾讯会议实现LabVIEW远程开发
利用向日葵远程控制软件结合微信或腾讯会议的视频通话功能,可以实现LabVIEW的远程开发和调试。通过向日葵进行远程桌面访问,配合视频通话工具进行实时沟通与问题解决,不仅提高了开发效率,还减少了地域限制带来的不便。介绍这种远程…...
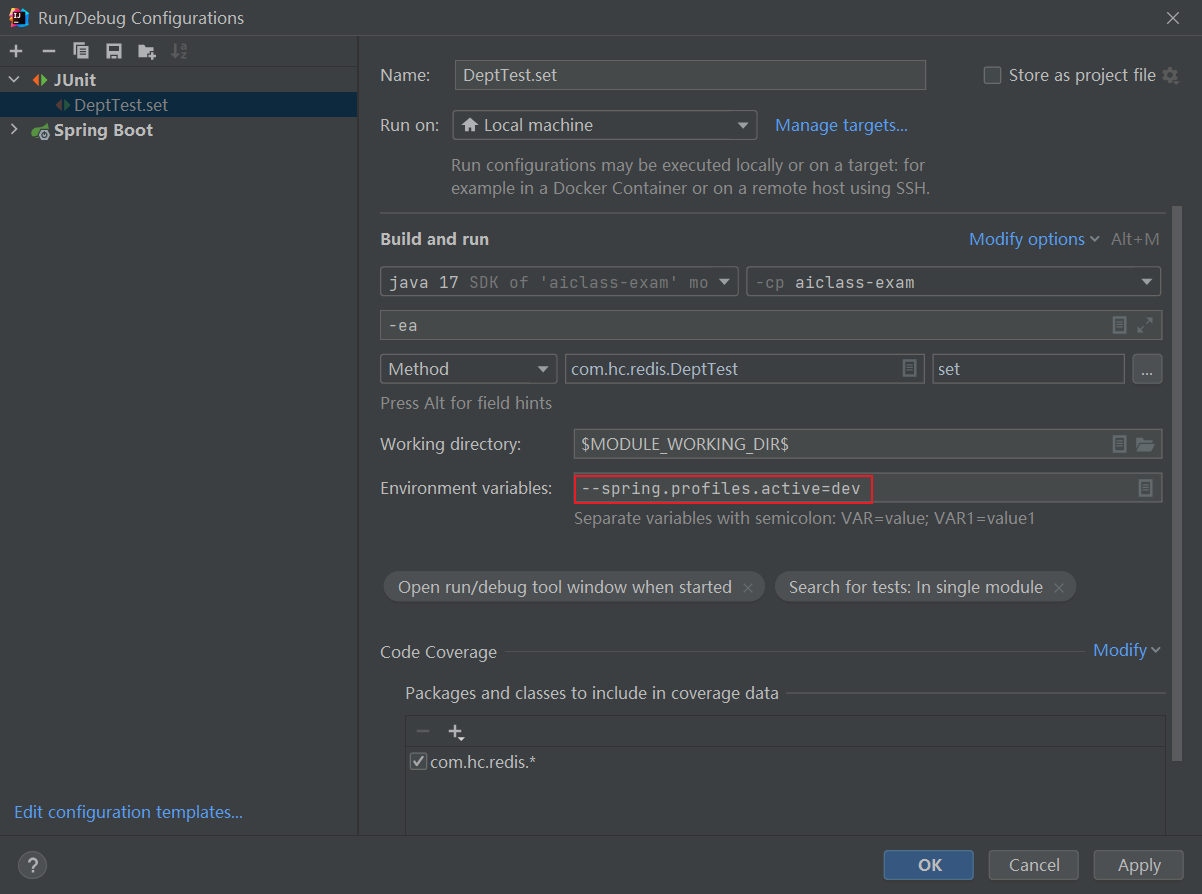
SpringBoot 单元测试 指定 环境
如上图所示,在配置窗口中添加--spring.profiles.activedev,就可以了。...

Flutter 中的 SliverOpacity 小部件:全面指南
Flutter 中的 SliverOpacity 小部件:全面指南 Flutter 是一个功能强大的 UI 框架,由 Google 开发,允许开发者使用 Dart 语言来构建高性能、美观的跨平台应用。在 Flutter 的滚动组件体系中,SliverOpacity 是一个用来为其子 Slive…...

源码分析の前言
源码分析路线图: 初级部分:ArrayList->LinkedList->Vector->HashMap(红黑树数据结构,如何翻转,变色,手写红黑树)->ConcurrentHashMap 中级部分:Spring->Spring MVC->Spring Boot->M…...
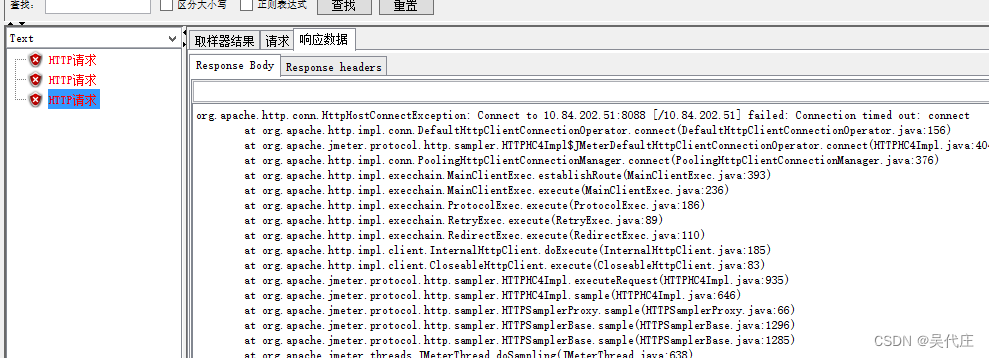
接口性能测试复盘:解决JMeter超时问题的实践
在优化接口并重新投入市场后,我们面临着一项关键任务:确保其在高压环境下稳定运行。于是,我们启动了一轮针对该接口的性能压力测试,利用JMeter工具模拟高负载场景。然而,在测试进行约一分钟之后,频繁出现了…...

[数据集][目标检测]猕猴桃检测数据集VOC+YOLO格式1838张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):1838 标注数量(xml文件个数):1838 标注数量(txt文件个数):1838 标注…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
