用r语言处理 Excel数据当中的缺失值方法
以下是使用 R 编程语言处理 Excel 缺失数据的一些常见方法示例代码:(无需循环)
读取包含缺失数据的 Excel 文件
data <- read.csv(“your_file.csv”)
查看数据中是否有缺失值
sum(is.na(data))
用平均值填充缺失值
data c o l u m n n a m e [ i s . n a ( d a t a column_name[is.na(data columnname[is.na(datacolumn_name)] <- mean(data$column_name, na.rm = TRUE)
用中位数填充缺失值
data c o l u m n n a m e [ i s . n a ( d a t a column_name[is.na(data columnname[is.na(datacolumn_name)] <- median(data$column_name, na.rm = TRUE)
请将 “your_file.csv” 替换为实际的 Excel 文件路径, “column_name” 替换为具体包含缺失值的列名。
相关文章:

用r语言处理 Excel数据当中的缺失值方法
以下是使用 R 编程语言处理 Excel 缺失数据的一些常见方法示例代码:(无需循环) 读取包含缺失数据的 Excel 文件 data <- read.csv(“your_file.csv”) 查看数据中是否有缺失值 sum(is.na(data)) 用平均值填充缺失值 data c o l u m …...

AWS 高防和阿里云高防深度对比
随着网络攻击的不断增加,企业对于网络安全的需求也越来越高。在这种情况下,高防护服务成为了企业网络安全的重要组成部分。AWS和阿里云作为全球领先的云计算服务提供商,都提供了高防护服务,但它们之间存在着一些差异。我们九河云一…...
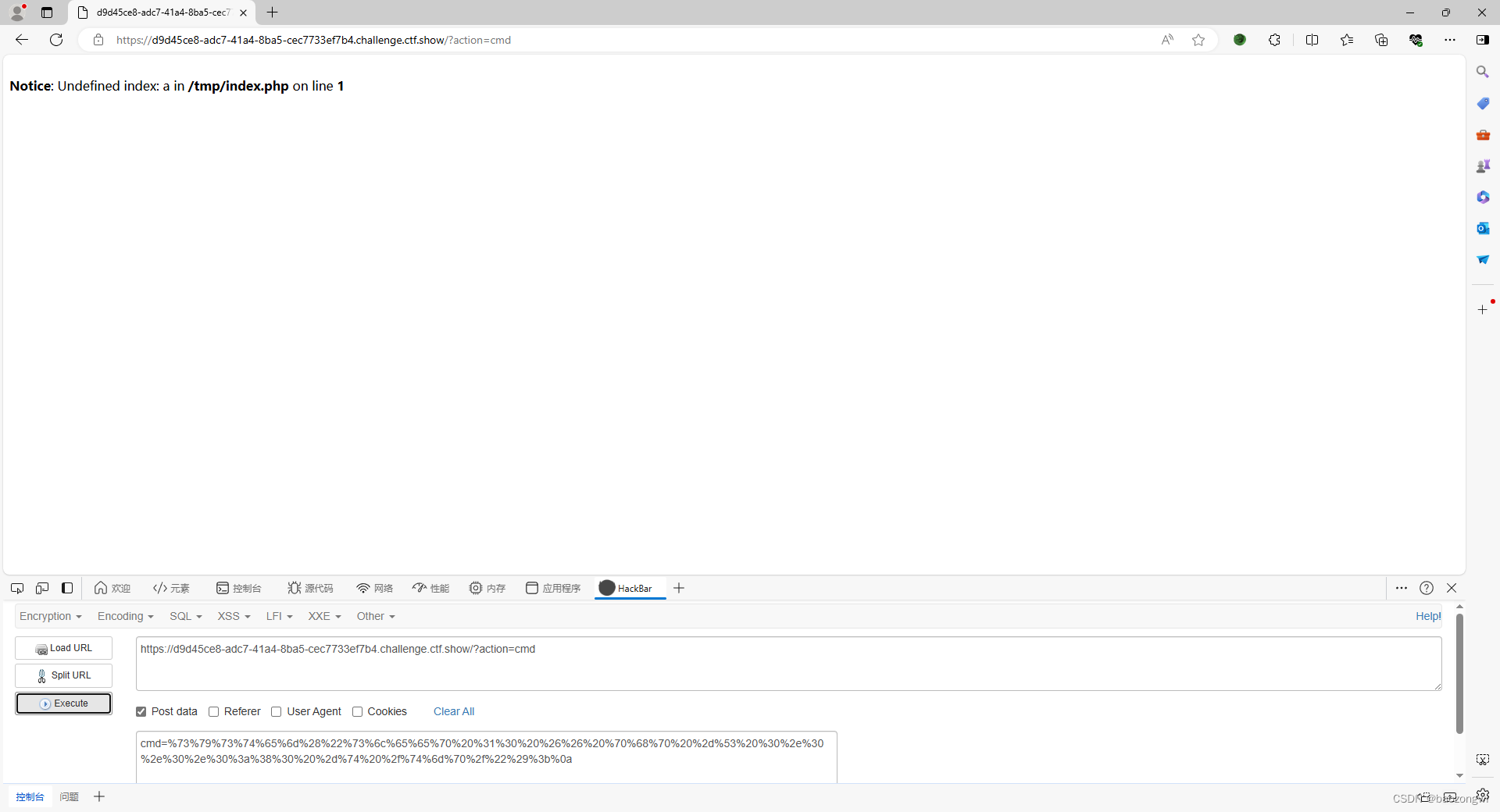
ctfshow web 月饼杯II
web签到 <?php //Author:H3h3QAQ include "flag.php"; highlight_file(__FILE__); error_reporting(0); if (isset($_GET["YBB"])) {if (hash("md5", $_GET["YBB"]) $_GET["YBB"]) {echo "小伙子不错嘛ÿ…...
)
「前端+鸿蒙」核心技术HTML5+CSS3(二)
1、开发者文档 开发者文档通常由浏览器厂商或技术社区提供,包含有关Web技术(如HTML、CSS、JavaScript)的详细信息,API文档,以及最佳实践。例如,MDN Web Docs是一个广泛认可的开发者资源。 2、块级元素与行列元素 块级元素:在页面上占据整行的元素,如<div>、<…...
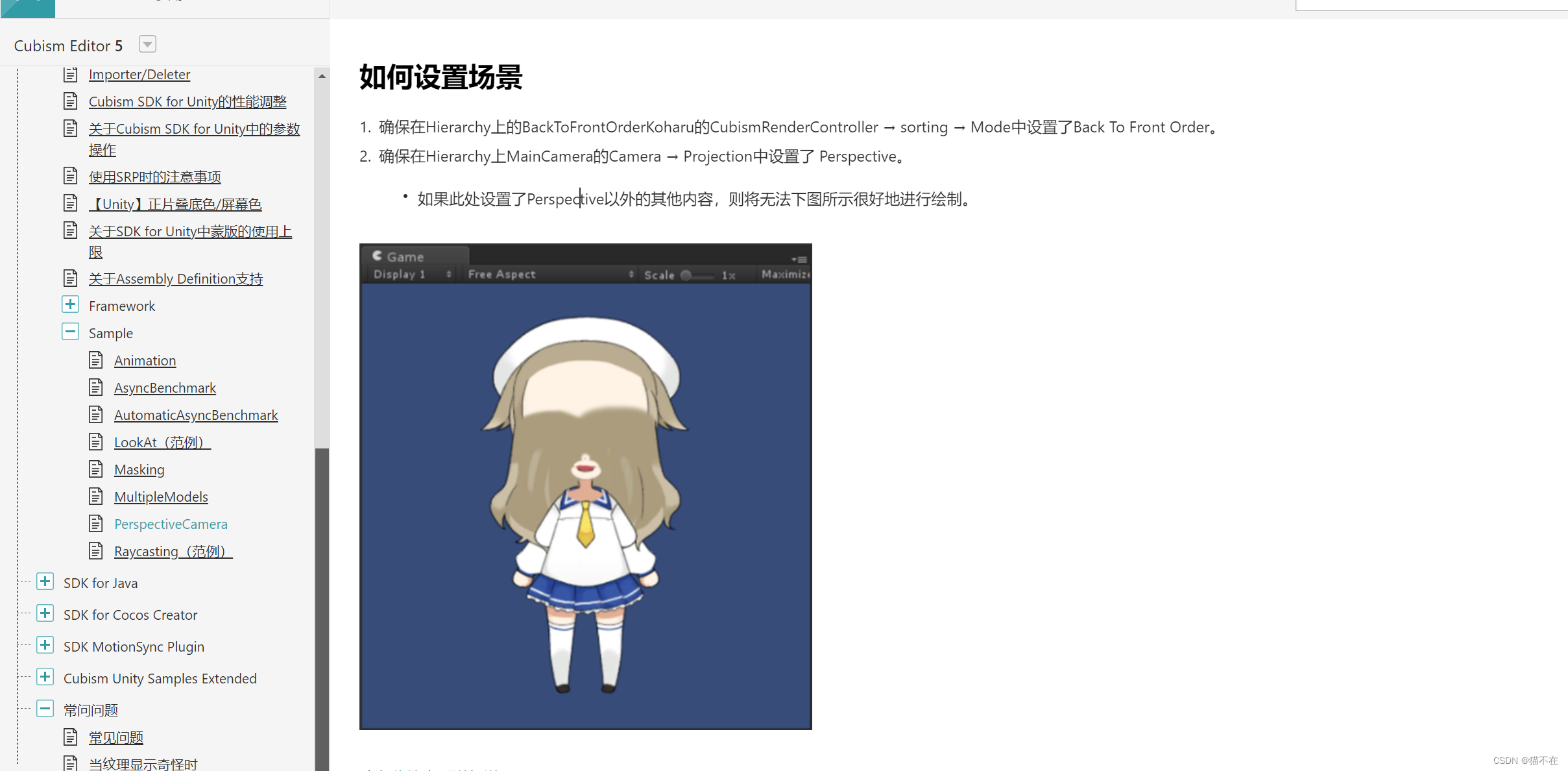
unity接入live2d
在bilibili上找到一个教程,首先注意一点,你直接导入那个sdk,并且打开示例,显示的模型是有问题的,你需要调整模型上脚本的一个枚举值,调整它的渲染顺序是front z to我看教程时候,很多老师都没有提…...

练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw. 第10题:在10维列向量构成的内积空间 V V V中…...

乐高小人分类项目
数据来源 LEGO Minifigures | Kaggle 建立文件目录 BASE_DIR lego/star-wars-images/ names [YODA, LUKE SKYWALKER, R2-D2, MACE WINDU, GENERAL GRIEVOUS ] tf.random.set_seed(1)# Read information about dataset if not os.path.isdir(BASE_DIR train/):for name in …...

个人关于ChatGPT的用法及建议
概述 这里只是个人常用的几个软件,做一下汇总,希望对各位有用。 如果有更高认知的朋友,请留下你的工具名称,提醒我一下,谢谢~ 常用的chatgpt模型工具: 以下是一些知名的例子: 文…...

神经网络的工程基础(二)——随机梯度下降法|文末送书
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 本文涉及到的代码链接如下:regression2chatgpt/ch06_optimizer/stochastic_gradient_descent.ipynb 本文将讨论利用…...

常见的几种编码方式
常见的编码方式及其特点: 编码方式的设计是为了适应不同的字符集和应用需求,因此它们在表示字符时使用的位数和字节数各不相同 常见编码方式及其位数和字节数 ASCII(American Standard Code for Information Interchange)&#x…...
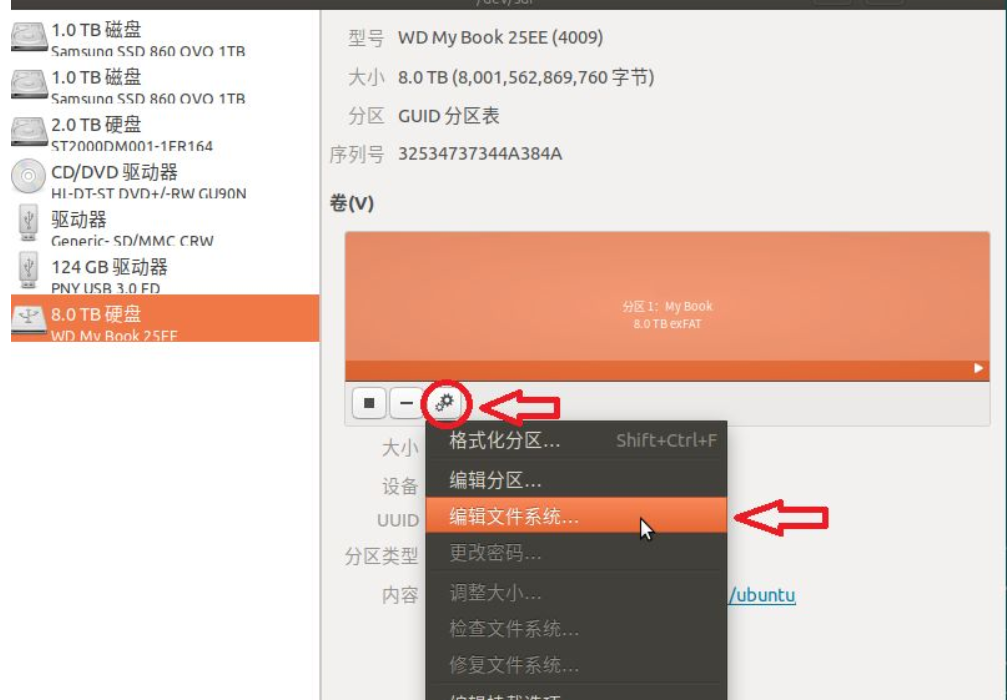
ubuntu移动硬盘重命名
因为在ubuntu上移动硬盘的名字是中文的,所以想要改成英文的。 我的方法: 将移动硬盘插到windows上,直接右键重命名。再插到ubuntu上名字就改变了。 别人的方法: ubuntu下如何修改U盘名字-腾讯云开发者社区-腾讯云 在自带的软件…...

VUE框架前置知识总结
一、前言 在学习vue框架中,总是有些知识不是很熟悉,又不想系统的学习JS,因为学习成本太大了,所以用到什么知识就学习什么知识。此文档就用于记录零散的知识点。主要是还是针对与ES6规范的JS知识点。 以下实验环境都是在windows环…...

张宇1000题80%不会?别急,这个方法肯定有用!
这太正常了,1000题的难度本来就高,不要慌 我考研的时候跟的也是张宇老师,但是1000题我根本就没做几道题就给换成880题660题了,而且只是强化阶段用880题,基础阶段我用的都是汤家凤的1800题。 不要担心做的不是张宇老师…...

【python】爬虫记录每小时金价
数据来源: https://www.cngold.org/img_date/ 因为这个网站是数据随时变动的,用requests、BeautifulSoup的方式解析html的话,数据的位置显示的是“--”,并不能取到数据。 所以采用webdriver访问网站,然后从界面上获取…...
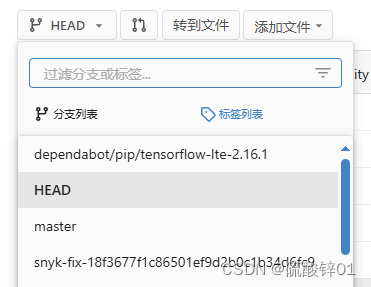
一行命令将已克隆的本地Git仓库推送到内网服务器
一、需求背景 我们公司用gitea搭建了一个git服务器,其中支持win7的最高版本是v1.20.6。 我们公司的电脑在任何时候都不能连接外网,但是希望将一些开源的仓库移植到内网的服务器来。一是有相关代码使用的需求,二是可以建设一个内网能够查阅的…...

Linux文本处理三剑客(详解)
一、文本三剑客是什么? 1. 对于接触过Linux操作系统的人来说,应该都听过说Linux中的文本三剑客吧,即awk、grep、sed,也是必须要掌握的Linux命令之一,三者都是用来处理文本的,但侧重点各不相同,a…...
AI在线UI代码生成,不需要敲一行代码,聊聊天,上传图片,就能生成前端页面的开发神器
ioDraw的在线UI代码生成器是一款开发神器,它可以让您在无需编写一行代码的情况下创建前端页面。 主要优势: 1、极简操作:只需聊天或上传图片,即可生成响应式的Tailwind CSS代码。 2、节省时间:自动生成代码可以节省大…...

go-zero整合单机版ClickHouse并实现增删改查
go-zero整合单机版ClickHouse并实现增删改查 本教程基于go-zero微服务入门教程,项目工程结构同上一个教程。 本教程主要实现go-zero框架整合单机版ClickHouse,并暴露接口实现对ClickHouse数据的增删改查。 go-zero微服务入门教程:https://b…...
行政工作如何提高效率?桌面备忘录便签软件哪个好
在行政管理工作中,效率的提高无疑是每个行政人员都追求的目标。而随着科技的发展,各种便捷的工具也应运而生,其中桌面备忘录便签软件便是其中的佼佼者。那么,这类软件又如何帮助我们提高工作效率呢? 首先,…...

利用向日葵和微信/腾讯会议实现LabVIEW远程开发
利用向日葵远程控制软件结合微信或腾讯会议的视频通话功能,可以实现LabVIEW的远程开发和调试。通过向日葵进行远程桌面访问,配合视频通话工具进行实时沟通与问题解决,不仅提高了开发效率,还减少了地域限制带来的不便。介绍这种远程…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
