Dijkstra求最短路篇一(全网最详细讲解两种方法,适合小白)(python,其他语言也适用)
前言:
Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。
本篇博客讲解朴素Dijkstra算法,第二篇博客讲解堆优化Dijkstra算法Dijkstra求最短路篇二(全网最详细讲解两种方法,适合小白)(python,其他语言也适用),两中算法思路大体相同,但时间复杂度有所区别。
- 朴素Dijkstra算法:时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 堆优化Dijkstra算法:时间复杂度 O ( m l o g n ) O(mlogn) O(mlogn)
两篇博客给出的题目内容一样,只有数据规模不一样。
题目:
题目链接:
849. Dijkstra求最短路 I
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围(两题不同处)
1 ≤ n ≤ 500 1≤n≤500 1≤n≤500,
1 ≤ m ≤ 1 0 5 1≤m≤10^5 1≤m≤105。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
Dijkstra算法介绍:
Dijkstra求最短路问题是图论的经典问题,首先介绍一下Dijkstra算法的流程图:
迪杰斯特拉算法采用的是一种贪心的策略。
求源点到其余各点的最短距离步骤如下:
- 用一个 dist 数组保存源点到其余各个节点的距离,dist[i] 表示源点到节点 i 的距离。初始时,dist数组的各个元素为无穷大。
用一个状态数组 state 记录是否找到了源点到该节点的最短距离,state[i] 如果为真,则表示找到了源点到节点 i 的最短距离,state[i] 如果为假,则表示源点到节点 i 的最短距离还没有找到。初始时,state 各个元素为假。
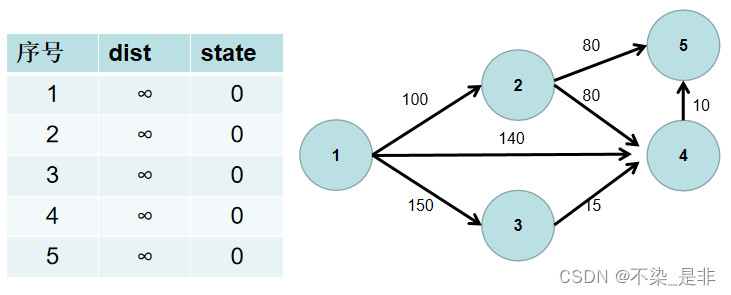
- 源点到源点的距离为 0。即dist[1] = 0。
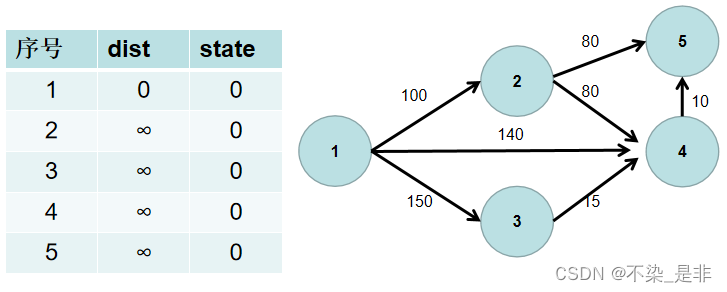
- 遍历 dist 数组,找到一个节点,这个节点是:没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离,state[i] 置为 1。
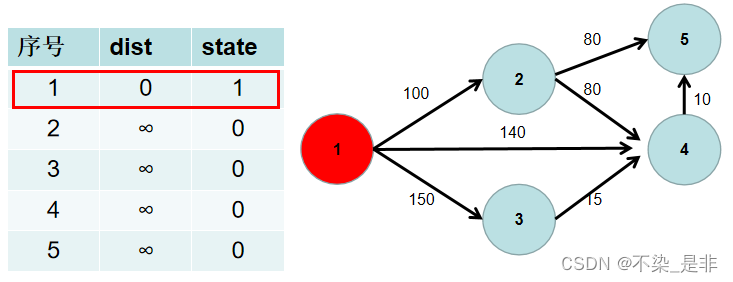
- 遍历 i 所有可以到达的节点 j,如果 dist[j] 大于 dist[i] 加上 i -> j 的距离,即 dist[j] > dist[i] + w[i][j](w[i][j] 为 i -> j 的距离) ,则更新 dist[j] = dist[i] + w[i][j]。
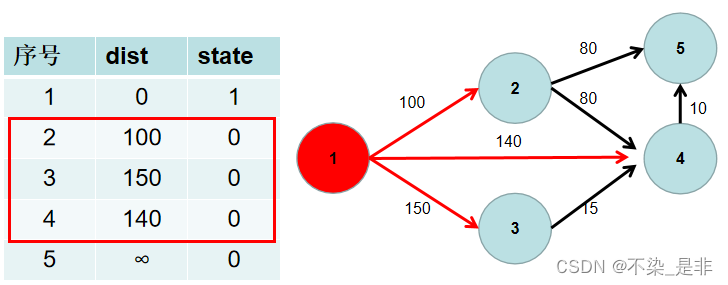
- 重复 3 4 步骤,直到所有节点的状态都被置为 1。
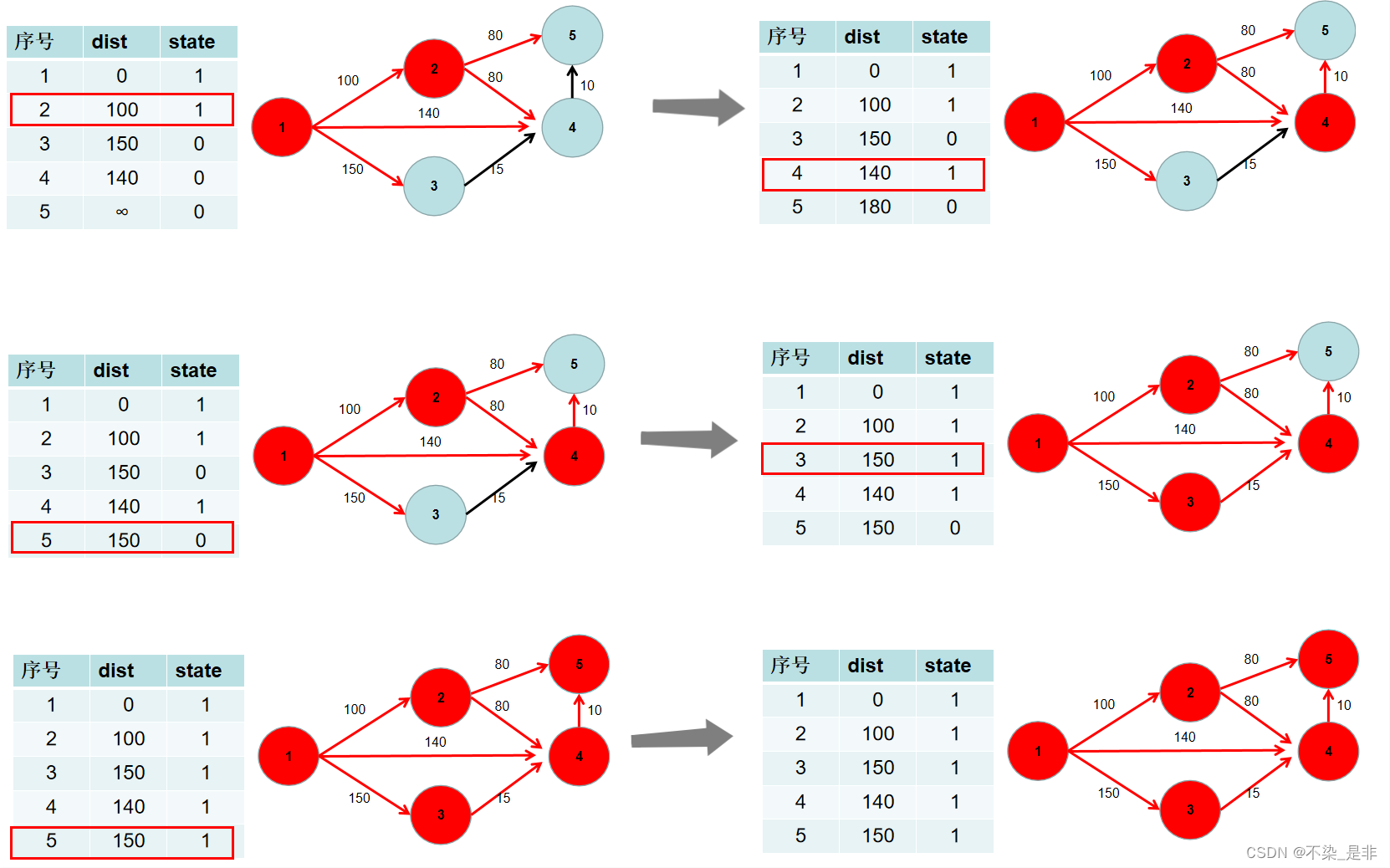
- 此时 dist 数组中,就保存了源点到其余各个节点的最短距离。
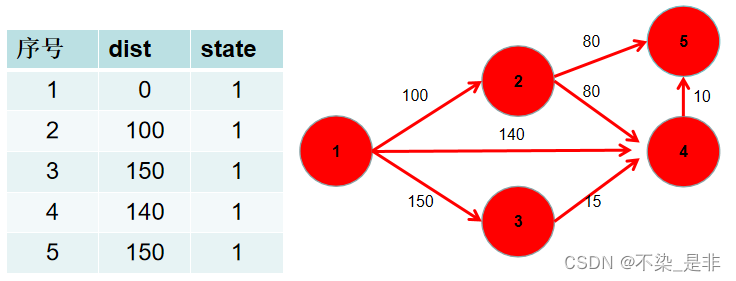
思路:
首先对数据进行存储,图的存储有两种方式,一种是邻接表,一种是邻接矩阵。题目中的数据规模用邻接矩阵存储(本题数据规模是稠密图,更省空间)。
为什么要用邻接矩阵去存贮,而不是邻接表?
我们采用邻接矩阵还是采用邻接表来表示图,需要判断一个图是稀疏图还是稠密图。稠密图指的是边的条数|E|接近于|V|²,稀疏图是指边的条数|E|远小于于|V|²(数量级差很多)。本题是稠密图,显然稠密图用邻接矩阵存储比较节省空间,反之用邻接表存储。
这里需要注意的是,题目中指出图中可能存在重边和自环。
- 重环是指两个点之间有多条边,每个边的距离不同。
- 自环是指一个点存在一条连向自己的边。
所以为了解决重环和自环问题,存储过程中需要存距离的最小值
邻接矩阵存储代码如下:
n, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接矩阵 float("inf")在python中是无限大的意思
num = [[float("inf") for j in range(n + 1)] for i in range(n + 1)]
for i in range(m):a, b, c = map(int, input().split())num[a][b] = min(num[a][b], c)
以题目实例为例,打印num数组(这里存储的是有向边,所以不是关于对角线对称的):
[[inf, inf, inf, inf], [inf, inf, 2, 4], [inf, inf, inf, 1], [inf, inf, inf, inf]]
邻接矩阵构建完成之后就要进行Dijkstra算法,这里直接给出代码,用详细代码给大家进行讲解。
代码及详细注释:
n, m = map(int, input().split()) # 图的节点个数和边数
# 构建邻接矩阵 float("inf")在python中是无限大的意思
num = [[float("inf") for j in range(n + 1)] for i in range(n + 1)]
for i in range(m):a, b, c = map(int, input().split())num[a][b] = min(num[a][b], c)
dist = [float('inf') for _ in range(n + 1)] # dist 数组用于记录每一个点距离第一个点的距离
dist[1] = 0 # 源点到源点的距离为置为 0
state = [False for _ in range(n + 1)] # state 用于记录该点的最短距离是否已经确定def dijkstra():for i in range(n): # 有n个点所以要进行n次迭代 (这里迭代多了并不影响结果,因为有state数组来记录每个点的状态)t = -1 # 该点不唯一,只要是在n个节点之外或者是最后一个节点就行(也可以是0,-1表示最后一个节点)for j in range(1, n + 1): # 循环每个点,找到最短距离的点,并把它赋值给t,(j表示各个节点)if not state[j] and dist[j] < dist[t]: # 该点未找到最短距离,且j点到第一个点的距离小于t点到第一个点的距离t = jstate[t] = True # 标记该点距离确定for j in range(1, n + 1): # # 根据该点更新其他所有点的距离dist[j] = min(dist[j], dist[t] + num[t][j])# 判断最后一个点的最短距离是否找到,如果为无穷大,则表示未找到,返回-1,否则返回最短距离dist[-1]if dist[n] == float('inf'):return -1else:return dist[-1]print(dijkstra())代码看着稍微复杂点,但拿实例数据跟着过一遍就一目了然。
这里拿实例带大家过一遍:
- 首先进行迭代,给t赋值为最后一个点(点3)的索引(索引值为-1,写n也可以)。之后循环这三个点,只有点1的dist距离(0)是小于最后一个点的dist值的(无穷大),所以 state[1] = True,然后循环所有的点,更新所有点到源点(点1始终是源点)的距离,dist[2] = 2, dist[3] = 4(点1与点2和点3直接相连,直接更新当前距离即可)
- 然后给t重新赋值为-1(这点很关键,不然之后都是跟点1进行比较了,算不出结果)。循环所有点后发现只有点2dist距离(2)是小于最后一个点的dist距离的(4)(点1的state为True,也就是已经找到最短距离了,不参与其中),之后都是重复第一步操作,更新dist[3] = 3
- 再一次循环时未更新值,只是把state[3] = True 的最短距离更新了,之后就会输出结果3
下面也会对大家难以理解的问题进行讲解回答(重点!!!):
t为什么要赋值为-1?
答:由于每一次都要找到还没有确定最短路距离的所有点中,距离当前的点最短的点(也就是始终为无穷大的值的点)。t = - 1是为了在st这个集合中找第一个点更新时候的方便所设定的(也可以是0,因为题目中不存在点0,但0的索引确始终存d在)。
- 为什么要进行n次迭代,dijkstra函数中
for i in range(n):的意义是什么?
答:这里的每次迭代主要是更新state数组的最短距离是否被找到,每一次迭代都会固定一个点的最短距离。
- 如果是问编号a到b的最短距离该怎么改呢?
初始化时 dist[a]=0, 以及返回时return dist[b]
- 为什么dist要初始化为无穷,邻接矩阵的部分点用无穷表示呢?
答:首先对于邻接矩阵而言,存储的是两点之间边的距离,如果两点之间不存在边,那肯定用无穷大来表示到达不了,dist数组初始化无穷大是因为这里要求最短路径,需要初始化一个较大值,这里初始化无穷大以免出错。
总结:
朴素版dijkstra适合稠密图
思路:
集合S为已经确定最短路径的点集。
- 初始化距离 一号结点的距离为零,其他结点的距离设为无穷大(看具体的题)。
- 循环n次,每一次将集合S之外距离最短X的点加入到S中去(这里的距离最短指的是距离1号点最近。 点X的路径一定最短,基于贪心,严格证明待看)。然后用点X更新X邻接点的距离。
时间复杂度分析:
- 寻找路径最短的点: O ( n 2 ) O(n^2) O(n2)
- 加入集合S: O ( n ) O(n) O(n)
- 更新距离: O ( m ) O(m) O(m)
- 所以总的时间复杂度为 O ( n 2 ) O(n^2) O(n2)
相关文章:

Dijkstra求最短路篇一(全网最详细讲解两种方法,适合小白)(python,其他语言也适用)
前言: Dijkstra算法博客讲解分为两篇讲解,这两篇博客对所有有难点的问题都会讲解,小白也能很好理解。看完这两篇博客后保证收获满满。 本篇博客讲解朴素Dijkstra算法,第二篇博客讲解堆优化Dijkstra算法Dijkstra求最短路篇二(全网…...

计算机组成原理06:浮点数运算
浮点数加减运算 之前我们提到过,浮点数具有特定的表示形式。因此,在进行浮点数的加减运算之前,需要统一浮点数的表达方式。这里我们主要对浮点数表示中的尾数M进行处理,要求0≤M<1,统一格式如下: 正数…...

opencascade 快速显示AIS_ConnectedInteractive源码学习
AIS_ConcentricRelation typedef PrsDim_ConcentricRelation AIS_ConcentricRelation AIS_ConnectedInteractive 简介 创建一个任意位置的另一个交互对象实例作为参考。这允许您使用连接的交互对象,而无需重新计算其表示、选择或图形结构。这些属性是从您的参考对…...

CentOS系统上安装单机版Redis教程
一、前言 1.1 为什么选择Redis? Redis不仅支持丰富的数据类型(如字符串、哈希、列表、集合、有序集合等),还具有高性能、持久化、发布订阅、事务和Lua脚本等特点。这些优势使其成为分布式系统和高并发应用中的首选。 1.2 为什么…...
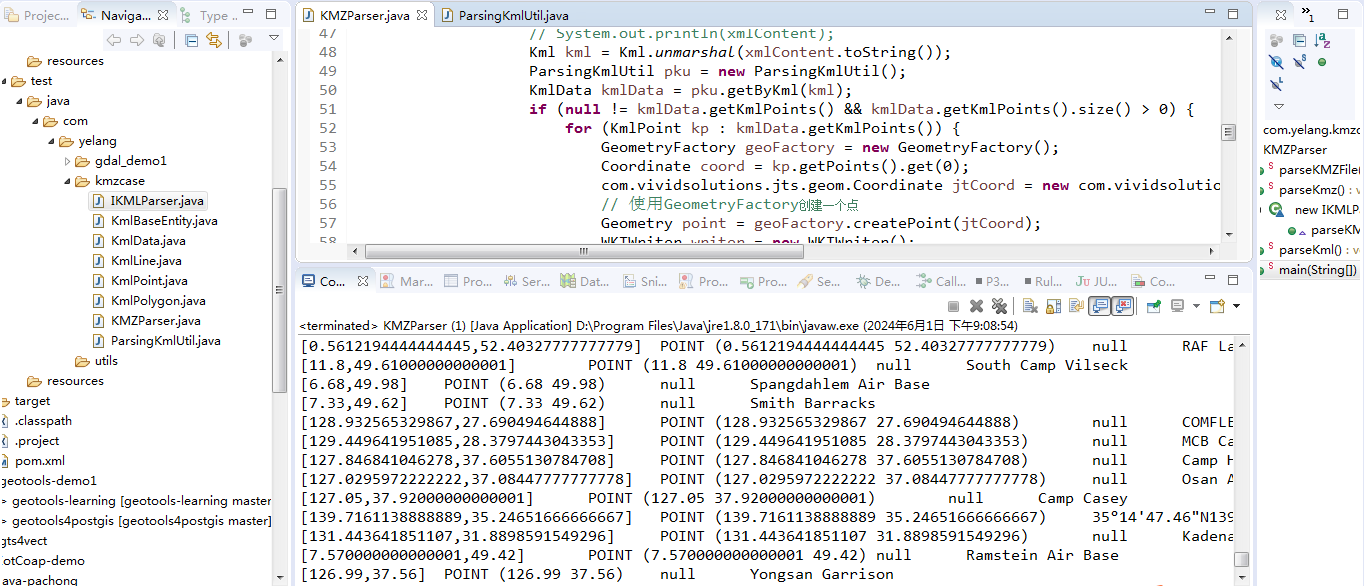
纯Java实现Google地图的KMZ和KML文件的解析
目录 前言 一、关于KMZ和KML 1、KMZ是什么 2、KML是什么 二、Java解析实例 1、POM.xml引用 2、KML 基类定义 3、空间对象的定义 4、Kml解析工具类 三、KML文件的解析 1、KML解析测试 2、KMZ解析测试 四、总结 前言 今天是六.一儿童节,在这里祝各位大朋友…...

k8s自定义资源你会创建吗
创建自定义资源定义 CustomResourceDefinition 当你创建新的 CustomResourceDefinition(CRD)时,Kubernetes API 服务器会为你所 指定的每一个版本生成一个 RESTful 的 资源路径。CRD 可以是名字空间作用域的,也可以是集群作用域的…...
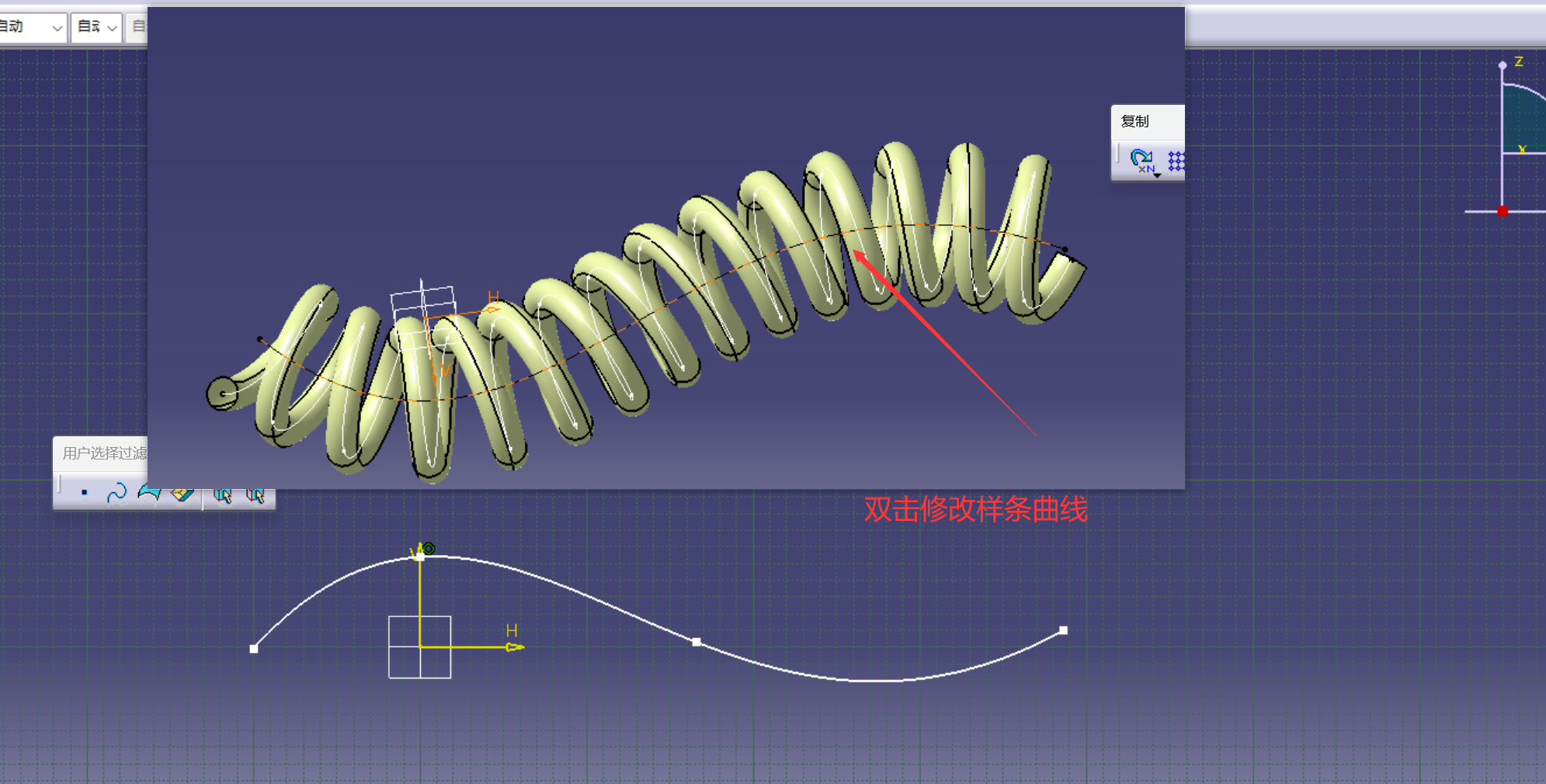
CATIA二次开发VBA入门(4)——进程外开发环境搭建,vb.net在Visual Studio中开发,创建圆柱曲面的宏录制到二次开发案例
目录 引出vb.net和vb6.0 进程外开发环境搭建vb.net开发环境搭建《CATIA二次开发技术基础》模板 添加宏库引用 vs开发环境初步vs中的立即窗口对象浏览器 建立模板案例:创建一堆圆柱曲面第一步:录制宏第二步:代码精简第三步:for循环…...

c++字符串相关接口
c字符串相关接口 1.str2wstr(str转换wstr)2.wstr2str(str转换wstr)3.Utf8ToAsi(Utf8转换ANSI)4.AsiToUtf8(ANSI转换Utf8)5.stringformatA/stringformatW(按照指定的格式格式化字符串)6.GetStringBetween(获取cStart cEnd之间的字符串)7.Char2Int(char转int)8.Str2Bin(字符串转换…...
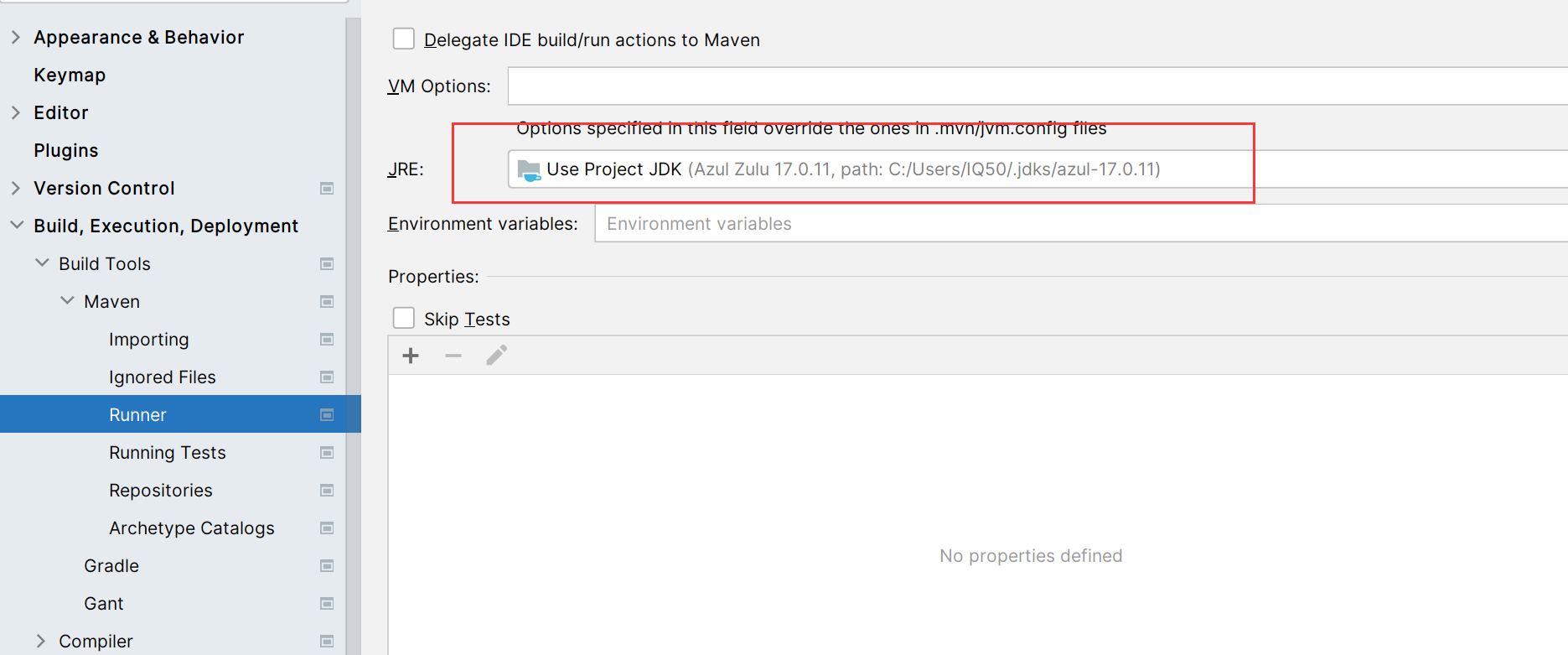
Maven打包错误:无效的源发行版:17
1. 报错问题 在用maven进行打包时(clean & install),报如下错误: 一开始让我很摸不着头脑,我确定我的pom.xml,还有IDEA中的Project Settings是正确的。 2. 排查 尽管确定,但还是一个个排…...

【环境栏Composer】Composer常见问题(持续更新)
1、执行composer install提示当前目录中没有 composer.lock 文件时 No composer.lock file present. Updating dependencies to latest instead of installing from lock file. See https://getcomposer.org/install for more information. Composer 在执行 install 命令时会…...

塑造更智慧的AI:策略与路径探索
提升数据质量: 数据清洗:去除数据中的异常值、缺失值、噪声等干扰因素,确保数据的准确性和一致性。数据标注:为数据集提供准确的标签,以便进行有监督学习。标注的质量直接影响模型的性能。数据增强:通过图像…...

软设之快速排序
快速排序是冒泡排序的改进算法 它采用的是分治法,基本思想是把原问题分解为若干规模更小但结构与原问题相似的子问题,通过递归解决这些子问题,然后将这些子问题的解组合成原问题的解。 它的步骤是 1.在待排序的n个记录中任取一个记录&…...

从零学算法2965
2965. 找出缺失和重复的数字 给你一个下标从 0 开始的二维整数矩阵 grid,大小为 n * n ,其中的值在 [1, n2] 范围内。除了 a 出现 两次,b 缺失 之外,每个整数都 恰好出现一次 。 任务是找出重复的数字a 和缺失的数字 b 。 返回一个…...
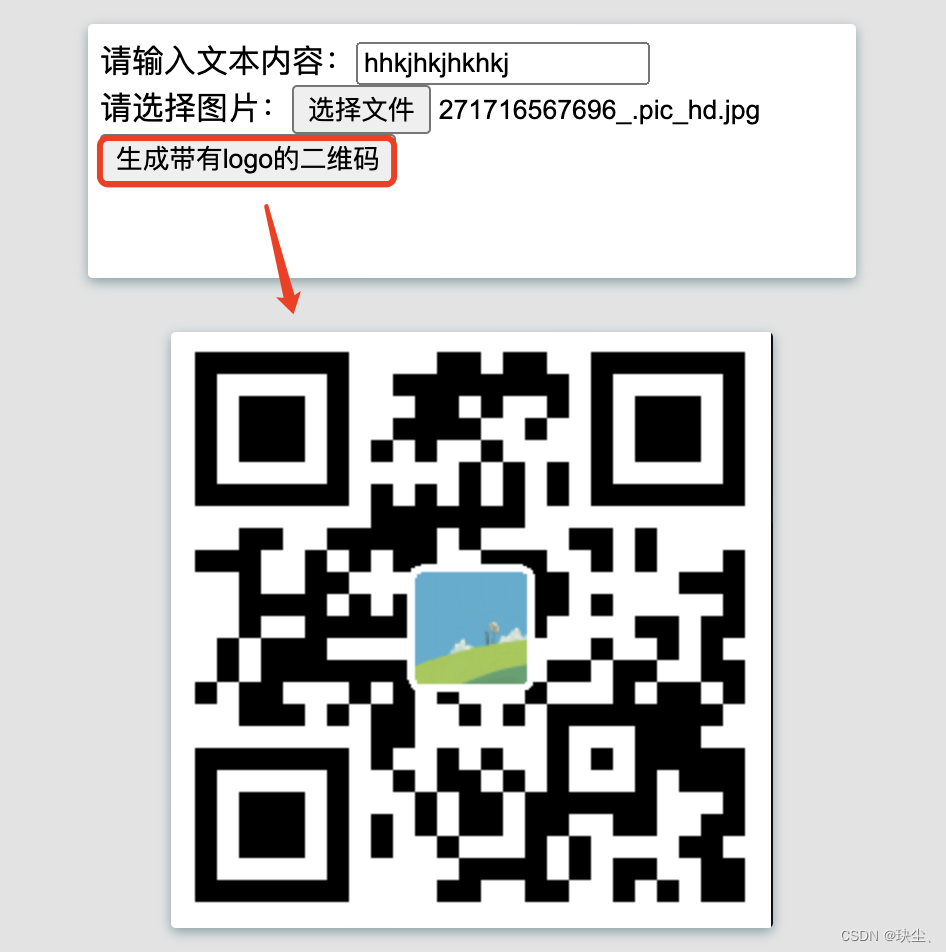
【Mac版】Java生成二维码
软件版本 IntelliJ IDEA:2023.2 JDK:17 Tomcat:10.1.11 Maven:3.9.3 技术栈 servlet谷歌的:zxing 生成普通的黑白二维码在二维码中间添加一个小图标 github开源项目:qrcode qrcode开源项目的内部是基于z…...

ROS2自定义服务接口
ROS2自定义服务接口 在src/village_interface 下构建srv文件夹 src/village_interface/srv 下新建一个BorrowMoney.srv 遵循大小写编程规范 # 客户端请求 string name uint32 money # 中间这三个横杠很重要 不能删掉 --- # 服务端响应 bool success uint32 money接口编译 修改…...
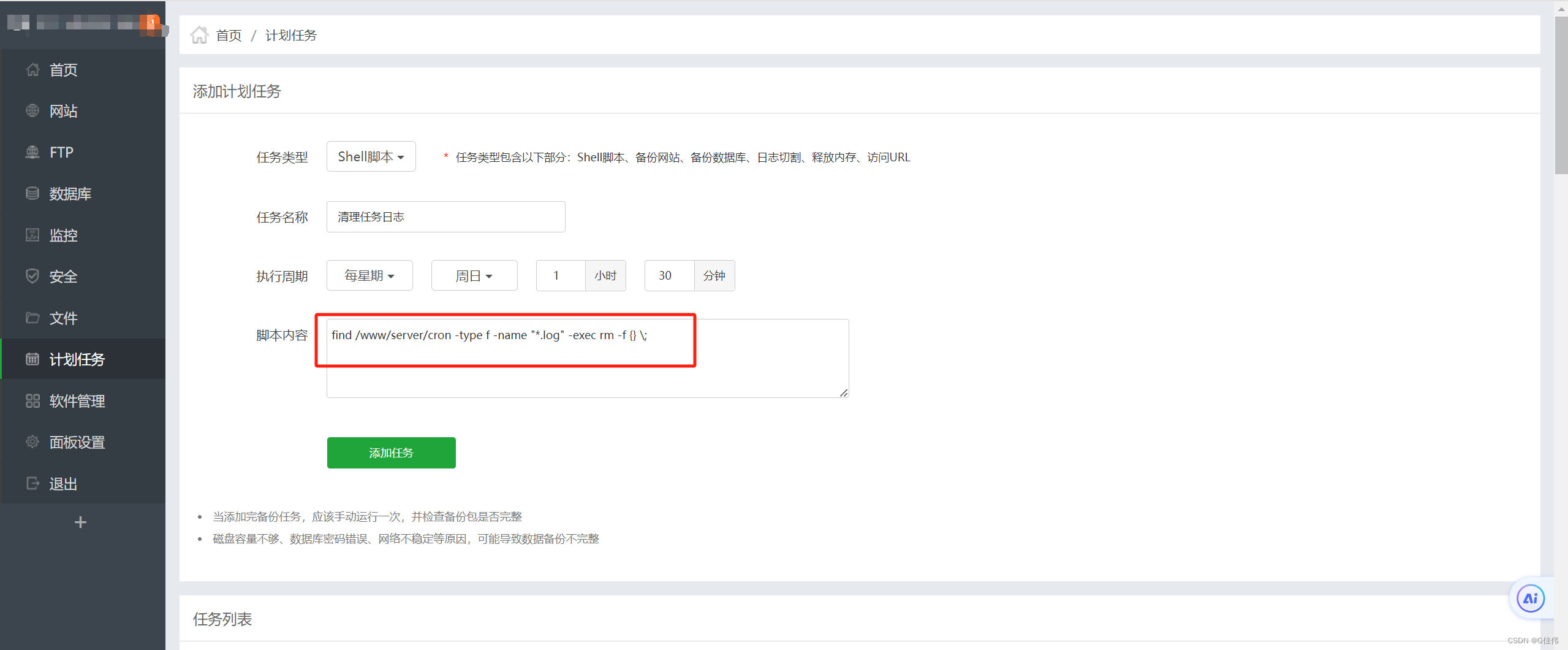
linux /www/server/cron内log文件占用空间过大,/www/server/cron是什么内容,/www/server/cron是否可以删除
linux服务器长期使用宝塔自带计划任务,计划任务执行记录占用服务器空间过大,导致服务器根目录爆满,需要长期排查并删除 /www/server/cron 占用空间过大问题处理 /www/server/cron是什么内容?/www/server/cron是否可以删除…...

C++青少年简明教程:break语句、continue语句
C青少年简明教程:break语句、continue语句 break语句 只能用在switch语句和循环语句(for循环、while循环和do-while循环)中。作用:跳出switch语句或提前终止循环。 break语句的基本语法如下: break; break语句的示例…...
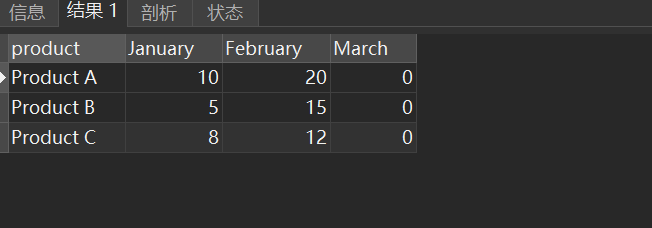
MySQL实战行转列(或称为PIVOT)实战sales的表记录了不同产品在不同月份的销售情况,进行输出
有一个sales的表,它记录了不同产品在不同月份的销售情况: productJanuaryFebruaryMarchProduct AJanuary10Product AFebruary20Product BJanuary5Product BFebruary15Product CJanuary8Product CFebruary12 客户需求展示为如下的样子: pro…...

牛客NC164 最长上升子序列(二)【困难 贪心+二分 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/4af96fa010c44638a7e112abf65f7237 思路 贪心二分 所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变…...

电子烟开发【恒压、恒有效算法】
恒压算法 pwm是通过软件模拟的 pwm满值运行是250全占空比 #define D_TARGET_AVERAGE_VOLTAGE 3500 //R_ADC1_Vout :发热丝两端AD值 //R_ADC_FVR :电池电压AD值 //FVR_VOLTAGE :电池AD参考电压 满电值AD //R_Smk1Duty :最后…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
