牛客NC164 最长上升子序列(二)【困难 贪心+二分 Java/Go/PHP/C++】
题目

题目链接:
https://www.nowcoder.com/practice/4af96fa010c44638a7e112abf65f7237
思路
贪心+二分
所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变得更长所以贪心的做法是,建立一个dp数组,dp[i[表示长度为i的LIS结尾元素的最小值,因此我们只需要维护dp数组即可对于每一个数组的数,我们对他们进行判断,如果他大于等于dp[ans]的值,就把他放在数组后面,dp[++ans] = tr[i],否则,就在dp中去找大一个大于等于他的位置pos,dp[pos] = tr[i]。如果从头扫一遍数组,时间复杂度还是O(n^2),这与曹贼何异?!通过观察我们知道,这次维护的dp数组是单调递增的,所以就可以使出秘技二分之lower_bound来找pos的位置我们举个栗子:tr[] = 2 5 18 3 4 7 10 9 11 8 15dp[1] = 2;5大于2,所以dp[2] = 518大于5,所以dp[3] = 183小于18,所以二分去找,pos是2,所以dp[2] = 34小于18,所以二分去找,pos是3,所以dp[3] = 47大于4,所以dp[4] = 710大于7,所以dp[5] = 109小于10,所以二分去找,pos是5,dp[5] = 911大于9,所以dp[6] = 118小于11,所以二分去找,pos是5,dp[5] = 815大于11,所以dp[7] = 15所以最长上升子序列的长度为7注意:dp数组得到的不一定是真正的LIS比如:tr[] = 1 4 7 2 5 9 10 3得到的是1 2 3 9 10,而真正的LIS是1 2 5 9 10因此dp数组得到的不一定是真正的LIS,他只表示最长子序列长度的排好序的最小序列,对于最后一半将5换成3的意义是记录最小序列,便于后续数据的处理
Java代码
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 该数组最长严格上升子序列的长度* @param a int整型一维数组 给定的数组* @return int整型*/public int LIS (int[] a) {//https://blog.csdn.net/weixin_51216553/article/details/114678534/*贪心+二分所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变得更长所以贪心的做法是,建立一个dp数组,dp[i[表示长度为i的LIS结尾元素的最小值,因此我们只需要维护dp数组即可对于每一个数组的数,我们对他们进行判断,如果他大于等于dp[ans]的值,就把他放在数组后面,dp[++ans] = tr[i],否则,就在dp中去找大一个大于等于他的位置pos,dp[pos] = tr[i]。如果从头扫一遍数组,时间复杂度还是O(n^2),这与曹贼何异?!通过观察我们知道,这次维护的dp数组是单调递增的,所以就可以使出秘技二分之lower_bound来找pos的位置我们举个栗子:tr[] = 2 5 18 3 4 7 10 9 11 8 15dp[1] = 2;5大于2,所以dp[2] = 518大于5,所以dp[3] = 183小于18,所以二分去找,pos是2,所以dp[2] = 34小于18,所以二分去找,pos是3,所以dp[3] = 47大于4,所以dp[4] = 710大于7,所以dp[5] = 109小于10,所以二分去找,pos是5,dp[5] = 911大于9,所以dp[6] = 118小于11,所以二分去找,pos是5,dp[5] = 815大于11,所以dp[7] = 15所以最长上升子序列的长度为7注意:dp数组得到的不一定是真正的LIS比如:tr[] = 1 4 7 2 5 9 10 3得到的是1 2 3 9 10,而真正的LIS是1 2 5 9 10因此dp数组得到的不一定是真正的LIS,他只表示最长子序列长度的排好序的最小序列,对于最后一半将5换成3的意义是记录最小序列,便于后续数据的处理*/int n = a.length;if (n <= 1) return n;int[] dp = new int[n + 1];int idx = 1;dp[idx] = a[0];// 利用贪心 + 二分查找进行更新for (int i = 1; i < n ; i++) {if (dp[idx] < a[i]) {idx++;dp[idx] = a[i];} else {int l = 1;int r = idx;int pos = 0;while (l <= r) {int mid = (l + r) >> 1;if (dp[mid] < a[i]) {pos = mid;l = mid + 1;} else {r = mid - 1;}}dp[pos + 1] = a[i];}}return idx;}
}
Go代码
package main/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 该数组最长严格上升子序列的长度* @param a int整型一维数组 给定的数组* @return int整型*/
func LIS(a []int) int {//https://blog.csdn.net/weixin_51216553/article/details/114678534/*贪心+二分所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变得更长所以贪心的做法是,建立一个dp数组,dp[i[表示长度为i的LIS结尾元素的最小值,因此我们只需要维护dp数组即可对于每一个数组的数,我们对他们进行判断,如果他大于等于dp[ans]的值,就把他放在数组后面,dp[++ans] = tr[i],否则,就在dp中去找大一个大于等于他的位置pos,dp[pos] = tr[i]。如果从头扫一遍数组,时间复杂度还是O(n^2),这与曹贼何异?!通过观察我们知道,这次维护的dp数组是单调递增的,所以就可以使出秘技二分之lower_bound来找pos的位置我们举个栗子:tr[] = 2 5 18 3 4 7 10 9 11 8 15dp[1] = 2;5大于2,所以dp[2] = 518大于5,所以dp[3] = 183小于18,所以二分去找,pos是2,所以dp[2] = 34小于18,所以二分去找,pos是3,所以dp[3] = 47大于4,所以dp[4] = 710大于7,所以dp[5] = 109小于10,所以二分去找,pos是5,dp[5] = 911大于9,所以dp[6] = 118小于11,所以二分去找,pos是5,dp[5] = 815大于11,所以dp[7] = 15所以最长上升子序列的长度为7注意:dp数组得到的不一定是真正的LIS比如:tr[] = 1 4 7 2 5 9 10 3得到的是1 2 3 9 10,而真正的LIS是1 2 5 9 10因此dp数组得到的不一定是真正的LIS,他只表示最长子序列长度的排好序的最小序列,对于最后一半将5换成3的意义是记录最小序列,便于后续数据的处理*/n := len(a)if n <= 1 {return n}dp := make([]int, n+1)idx := 1dp[idx] = a[0]//利用贪心+二分查找进行更新for i := 1; i < n; i++ {if dp[idx] < a[i] {idx++dp[idx] = a[i]} else {l := 1r := idxpos := 0for l <= r {mid := (l + r) >> 1if dp[mid] < a[i] {pos = midl = mid + 1} else {r = mid - 1}}dp[pos+1] = a[i]}}return idx
}PHP代码
<?php/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 该数组最长严格上升子序列的长度* @param a int整型一维数组 给定的数组* @return int整型*/
function LIS( $a )
{//https://blog.csdn.net/weixin_51216553/article/details/114678534/*贪心+二分所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变得更长所以贪心的做法是,建立一个dp数组,dp[i[表示长度为i的LIS结尾元素的最小值,因此我们只需要维护dp数组即可对于每一个数组的数,我们对他们进行判断,如果他大于等于dp[ans]的值,就把他放在数组后面,dp[++ans] = tr[i],否则,就在dp中去找大一个大于等于他的位置pos,dp[pos] = tr[i]。如果从头扫一遍数组,时间复杂度还是O(n^2),这与曹贼何异?!通过观察我们知道,这次维护的dp数组是单调递增的,所以就可以使出秘技二分之lower_bound来找pos的位置我们举个栗子:tr[] = 2 5 18 3 4 7 10 9 11 8 15dp[1] = 2;5大于2,所以dp[2] = 518大于5,所以dp[3] = 183小于18,所以二分去找,pos是2,所以dp[2] = 34小于18,所以二分去找,pos是3,所以dp[3] = 47大于4,所以dp[4] = 710大于7,所以dp[5] = 109小于10,所以二分去找,pos是5,dp[5] = 911大于9,所以dp[6] = 118小于11,所以二分去找,pos是5,dp[5] = 815大于11,所以dp[7] = 15所以最长上升子序列的长度为7注意:dp数组得到的不一定是真正的LIS比如:tr[] = 1 4 7 2 5 9 10 3得到的是1 2 3 9 10,而真正的LIS是1 2 5 9 10因此dp数组得到的不一定是真正的LIS,他只表示最长子序列长度的排好序的最小序列,对于最后一半将5换成3的意义是记录最小序列,便于后续数据的处理*/$n = count($a);if($n<=1){return $n;}$dp =[0];$idx = 1;$dp[$idx] = $a[0];// 利用贪心 + 二分查找进行更新for($i=1;$i<$n;$i++){if($dp[$idx] <$a[$i]){$idx++;$dp[$idx] = $a[$i];}else{$l=1;$r =$idx;$pos=0;while ($l<=$r){$mid = ($l+$r) >>1;if($dp[$mid] <$a[$i]){$pos = $mid;$l=$mid+1;}else{$r = $mid-1;}}$dp[$pos+1] = $a[$i];}}return $idx;
}
C++代码
class Solution {public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 该数组最长严格上升子序列的长度* @param a int整型vector 给定的数组* @return int整型*/int LIS(vector<int>& a) {//https://blog.csdn.net/weixin_51216553/article/details/114678534/*贪心+二分所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变得更长所以贪心的做法是,建立一个dp数组,dp[i[表示长度为i的LIS结尾元素的最小值,因此我们只需要维护dp数组即可对于每一个数组的数,我们对他们进行判断,如果他大于等于dp[ans]的值,就把他放在数组后面,dp[++ans] = tr[i],否则,就在dp中去找大一个大于等于他的位置pos,dp[pos] = tr[i]。如果从头扫一遍数组,时间复杂度还是O(n^2),这与曹贼何异?!通过观察我们知道,这次维护的dp数组是单调递增的,所以就可以使出秘技二分之lower_bound来找pos的位置我们举个栗子:tr[] = 2 5 18 3 4 7 10 9 11 8 15dp[1] = 2;5大于2,所以dp[2] = 518大于5,所以dp[3] = 183小于18,所以二分去找,pos是2,所以dp[2] = 34小于18,所以二分去找,pos是3,所以dp[3] = 47大于4,所以dp[4] = 710大于7,所以dp[5] = 109小于10,所以二分去找,pos是5,dp[5] = 911大于9,所以dp[6] = 118小于11,所以二分去找,pos是5,dp[5] = 815大于11,所以dp[7] = 15所以最长上升子序列的长度为7注意:dp数组得到的不一定是真正的LIS比如:tr[] = 1 4 7 2 5 9 10 3得到的是1 2 3 9 10,而真正的LIS是1 2 5 9 10因此dp数组得到的不一定是真正的LIS,他只表示最长子序列长度的排好序的最小序列,对于最后一半将5换成3的意义是记录最小序列,便于后续数据的处理*/int n = a.size();if (n <= 1) {return n;}vector<int> dp(n + 1, 0);int idx = 1;dp[idx] = a[0];// 利用贪心 + 二分查找进行更新for (int i = 1; i < n; i++) {if (dp[idx] < a[i]) {dp[++idx] = a[i];} else {int l = 1;int r = idx;int pos = 0;while (l <= r) {int mid = (l + r) >> 1;if (dp[mid] < a[i]) {pos = mid;l = mid + 1;} else {r = mid - 1;}}dp[pos + 1] = a[i];}}return idx;}
};
相关文章:

牛客NC164 最长上升子序列(二)【困难 贪心+二分 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/4af96fa010c44638a7e112abf65f7237 思路 贪心二分 所谓贪心,就是往死里贪,所以对于最大上升子序列,结尾元素越小,越有利于后面接上其他的数,也就可能变…...

电子烟开发【恒压、恒有效算法】
恒压算法 pwm是通过软件模拟的 pwm满值运行是250全占空比 #define D_TARGET_AVERAGE_VOLTAGE 3500 //R_ADC1_Vout :发热丝两端AD值 //R_ADC_FVR :电池电压AD值 //FVR_VOLTAGE :电池AD参考电压 满电值AD //R_Smk1Duty :最后…...

基于Open3D的点云处理22-非阻塞可视化/动态可视化
官网测试用例:examples/python/visualization/non_blocking_visualization.py 非阻塞可视化,即实时更新点云数据; 如下,动态可视化ICP的匹配过程: import open3d as o3d import numpy as npif __name__ == "__main__":o3d.utility.set_verbosity_level(o3d.ut…...

C++面试题其一
C和C的区别 C和C都是广泛使用的编程语言,但它们有显著的区别: 语言范式: C:是一种过程化编程语言,强调过程和函数的使用。C:是一种多范式编程语言,支持面向对象编程、泛型编程和过程化编程。 …...
CentOS7某天的samba服务搭建操作记录(还没成功)
#CentOS7 yum软件仓库阿里云 samba服务器配置失败 sensors成功了 (花了200元组装H61测试机,75元的主板只有一块能用,垃圾板但又不完全能用) 2024.5月的某天记录如下: https://blog.csdn.net/dszgf5717/article/details/53732182 …...
Qt Demo:基于TCP协议的视频传输Demo
目录 1.设计思路 2.Pro文件配置 3.头文件引入 4.界面设计 5.初始化设备函数 6.发起视频链接函数 7.初始化定时器模块函数 8.TCP链接模块函数 9.处理接收的数据线程函数 10.实现功能展示 设计思路 基于TCP协议的视频传输Demo,设计要实现的功能主要是TCP传输还有视频&…...

内存管理【C++】
内存分布 C中的内存区域主要有以下5种 栈(堆栈):存放非静态局部变量/函数参数/函数返回值等等,栈是向下增长的【地址越高越先被使用】。栈区内存的开辟和销毁由系统自动执行 堆:用于程序运行时动态内存分配ÿ…...

D3D 顶点格式学习
之前D3D画三角形的代码中有这一句, device.VertexFormat CustomVertex.TransformedColored.Format; 这是设置顶点格式; 画出的三角形如下, 顶点格式是描述一个三维模型的顶点信息的格式;可以包含以下内容, 位置…...
gmssl vs2010编译
1、虚拟机win10 x64,离线安装vs2010和2010sp1补丁; 2、安装ActivePerl_v5.28.1.0000和nasm-2.16.03-installer-x64均是默认完整安装; nasm官网下载: Index of /pub/nasm/releasebuilds/2.16.03/win64https://www.nasm.us/pub/nas…...
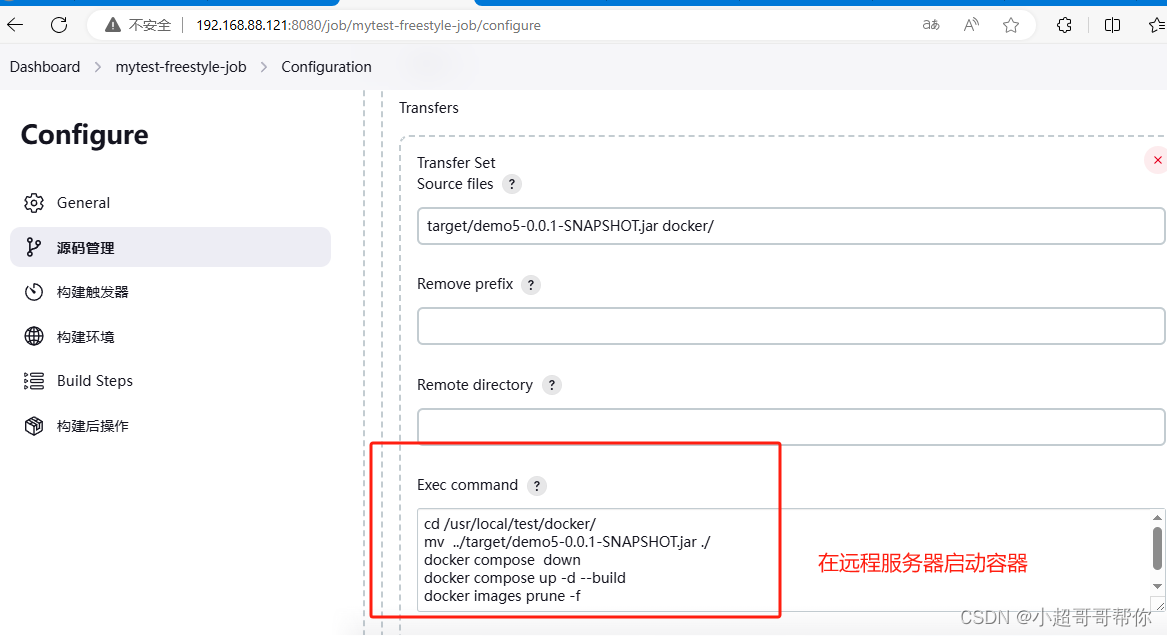
容器化部署gitlab、jenkins,jenkins应用示例
一、容器化部署docker和docker conpose安装 Docker&Docker-compose的安装及部署_docker 20 使用什么版本docker-compose-CSDN博客 1.docker 安装脚本 cat >01_docker.sh<<EOF #!/bin/bash yum remove docker \docker-client \docker-client-latest \docker-co…...
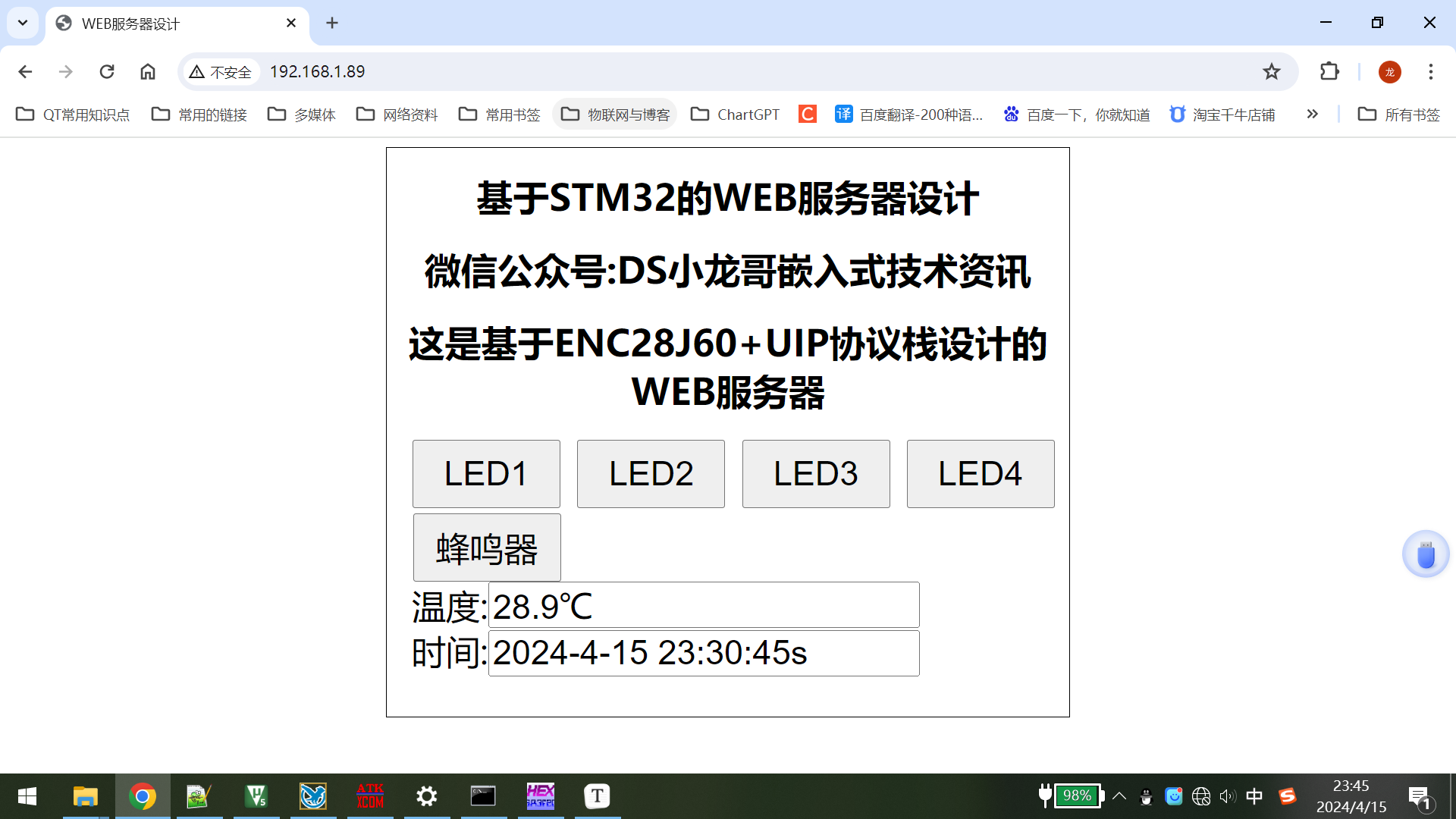
基于STM32的轻量级Web服务器设计
文章目录 一、前言1.1 开发背景1.2 实现的功能1.3 硬件模块组成1.4 ENC28J60网卡介绍1.5 UIP协议栈【1】目标与特点【2】核心组件【3】应用与优势 1.6 添加UIP协议栈实现创建WEB服务器步骤1.7 ENC28J60添加UIP协议栈实现创建WEB客户端1.8 ENC28J60移植UIP协议并编写服务器测试示…...

用r语言处理 Excel数据当中的缺失值方法
以下是使用 R 编程语言处理 Excel 缺失数据的一些常见方法示例代码:(无需循环) 读取包含缺失数据的 Excel 文件 data <- read.csv(“your_file.csv”) 查看数据中是否有缺失值 sum(is.na(data)) 用平均值填充缺失值 data c o l u m …...

AWS 高防和阿里云高防深度对比
随着网络攻击的不断增加,企业对于网络安全的需求也越来越高。在这种情况下,高防护服务成为了企业网络安全的重要组成部分。AWS和阿里云作为全球领先的云计算服务提供商,都提供了高防护服务,但它们之间存在着一些差异。我们九河云一…...
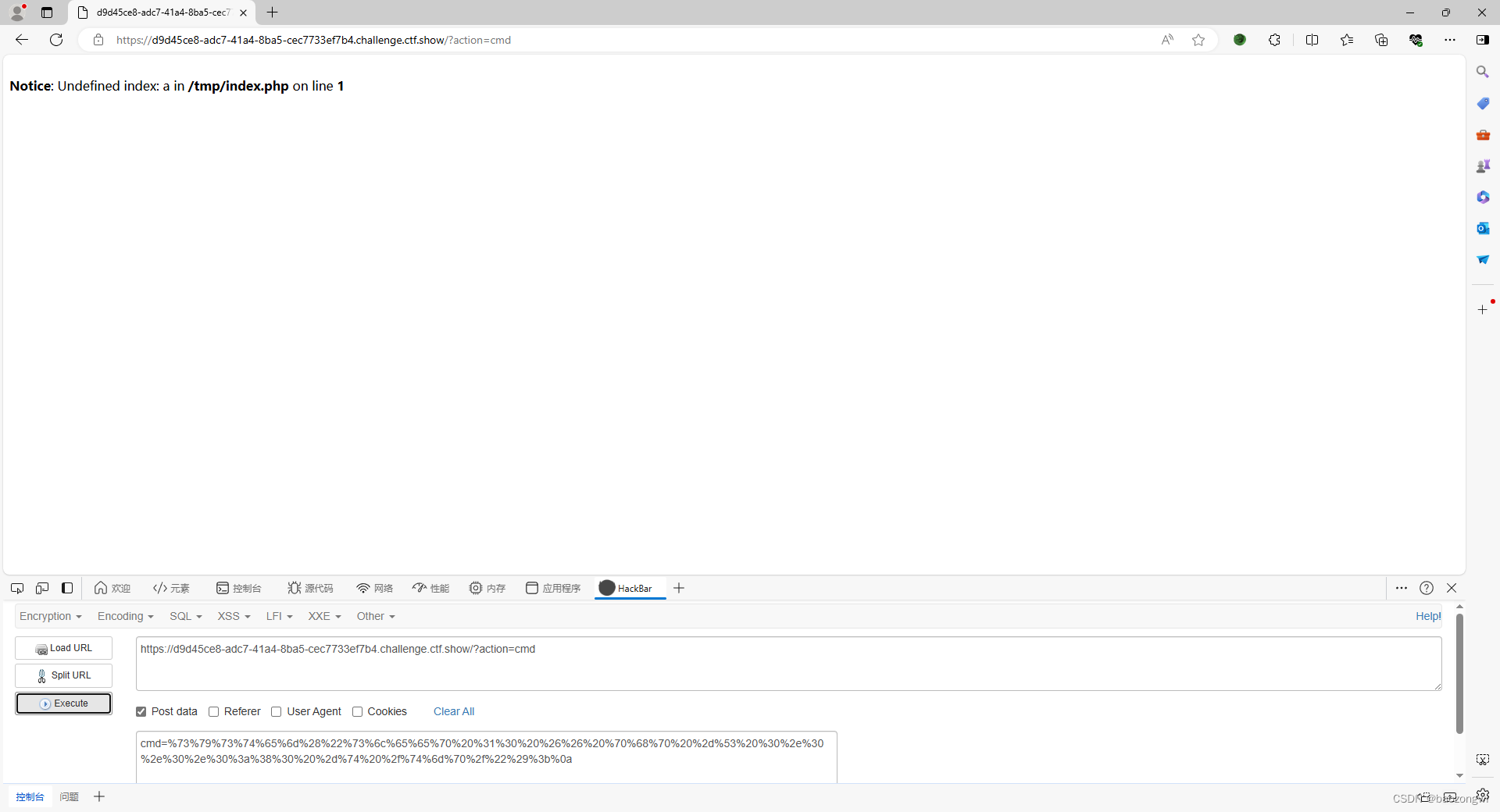
ctfshow web 月饼杯II
web签到 <?php //Author:H3h3QAQ include "flag.php"; highlight_file(__FILE__); error_reporting(0); if (isset($_GET["YBB"])) {if (hash("md5", $_GET["YBB"]) $_GET["YBB"]) {echo "小伙子不错嘛ÿ…...
)
「前端+鸿蒙」核心技术HTML5+CSS3(二)
1、开发者文档 开发者文档通常由浏览器厂商或技术社区提供,包含有关Web技术(如HTML、CSS、JavaScript)的详细信息,API文档,以及最佳实践。例如,MDN Web Docs是一个广泛认可的开发者资源。 2、块级元素与行列元素 块级元素:在页面上占据整行的元素,如<div>、<…...
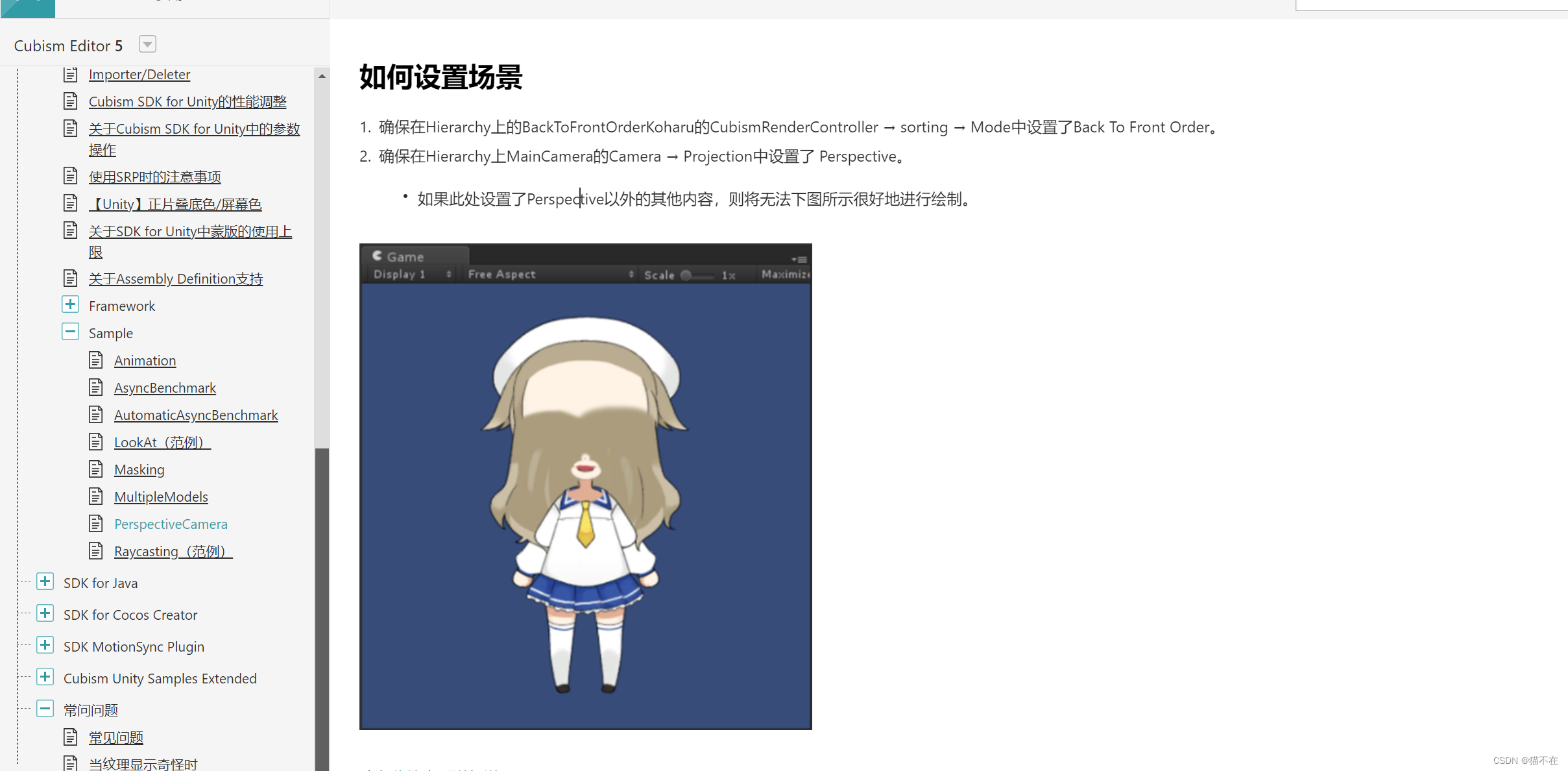
unity接入live2d
在bilibili上找到一个教程,首先注意一点,你直接导入那个sdk,并且打开示例,显示的模型是有问题的,你需要调整模型上脚本的一个枚举值,调整它的渲染顺序是front z to我看教程时候,很多老师都没有提…...

练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw. 第10题:在10维列向量构成的内积空间 V V V中…...

乐高小人分类项目
数据来源 LEGO Minifigures | Kaggle 建立文件目录 BASE_DIR lego/star-wars-images/ names [YODA, LUKE SKYWALKER, R2-D2, MACE WINDU, GENERAL GRIEVOUS ] tf.random.set_seed(1)# Read information about dataset if not os.path.isdir(BASE_DIR train/):for name in …...

个人关于ChatGPT的用法及建议
概述 这里只是个人常用的几个软件,做一下汇总,希望对各位有用。 如果有更高认知的朋友,请留下你的工具名称,提醒我一下,谢谢~ 常用的chatgpt模型工具: 以下是一些知名的例子: 文…...

神经网络的工程基础(二)——随机梯度下降法|文末送书
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 本文涉及到的代码链接如下:regression2chatgpt/ch06_optimizer/stochastic_gradient_descent.ipynb 本文将讨论利用…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
