【数据挖掘】3σ原则识别数据中的异常值(附代码)
写在前面:
首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。
路虽远,行则将至;事虽难,做则必成。只要有愚公移山的志气、滴水穿石的毅力,脚踏实地,埋头苦干,积跬步以至千里,就一定能够把宏伟目标变为美好现实。
今天给大家分享一个异常值处理的小方法,它的名字叫3σ原则,在实际项目中使用这个方法对异常数据进行处理,模型精度必须猛涨。多的不说,少的不唠,下面开始今天的教程。
1、引言
异常值是指数据样本中的一些数值明显偏离其他的样本值,这些偏离其他样本值的异常值也称离群点,异常值分析则也称为离群点分析。
在机器学习、数据分析、数据挖掘项目中,需要对数据集进行异常值处理(包括直接删除或者数据修正),这样处理的目的是方便后续更好地进行信息挖掘,减少噪声数据的干扰,提高分析的准确性[1]。
2、3σ原则
3σ原则,又叫拉依达原则,是一基于正态分布的数学原理,它假设一组检测数据中只含有随机误差,通过计算得到标准偏差σ,然后按一定概率确定一个区间,对于超过这个区间的误差,就不属于随机误差而是粗大误差,将含有粗大误差的数据进行剔除[2]。
在统计学中,如果一个变量服从正态分布,且它的均值是u, 标准差是σ,那么将有:
(1)68.27%的数据会落在 u ± σ 内,即数据分布在处于(u−σ, u+σ)中的概率是0.6827
(2)95.45%的数据会落在 u ± 2σ 内,即数据分布在处于(u−2σ, u+2σ)中的概率是0.9545
(3)99.73%的数据会落在 u ± 3σ 内,即数据分布在处于(u−3σ, u+3σ)中的概率是0.9973
通常认为,数据“Y”的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%,这些超出该范围的数据可以认为是异常值[2]。

(注:此部分内容为3σ原则的定义,已做了引用,无不良引导,不存在滥用原创的情况)
3、代码
3.1 数据
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm
import pandas as pd# 设置参数
s = 0.5 # 形状参数(σ),较小的值会导致更重的右尾
mean = 0 # 对数正态分布的底数(μ)对应的对数均值
scale = np.exp(s**2) # 尺度参数(exp(σ^2)),确保对数正态分布的方差正确
n_samples = 1000 # 样本数量 # 生成对数正态分布数据
data = lognorm.rvs(s=s, scale=scale, size=n_samples) # 写入excel
df = pd.DataFrame(data)
df.to_excel("data.xlsx", index=False, header=None)# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.6, color='g') # 绘制对数正态分布曲线作为参考
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
pdf_values = lognorm.pdf(x, s=s, scale=scale)
plt.plot(x, pdf_values, 'k', linewidth=2, label='Lognormal Distribution (s={})'.format(s)) # 设置图表标题和坐标轴标签
plt.title('Lognormal Distribution with Long Right Tail (s={})'.format(s))
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend() # 显示图形
plt.grid(True)
plt.show()
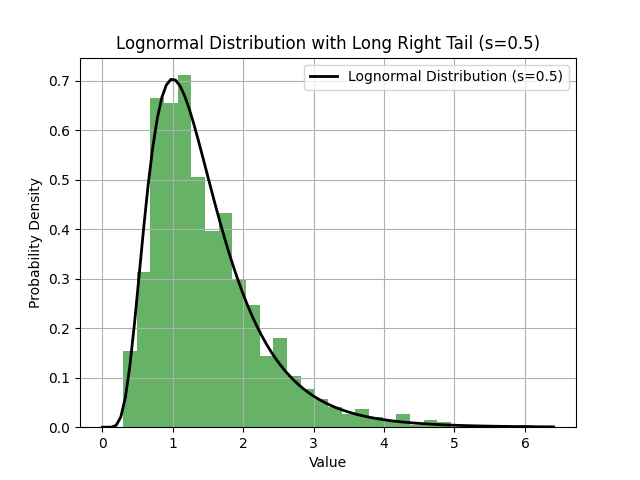
数据分布图如下:
3.2 3σ代码
def three_sigma(data_df, column):out_index = []mean_value = data_df[column].mean() # 求平均值std_value = data_df[column].std() # 求标准差# print("均值和标准差", mean_value, std_value)lower_bound = mean_value-3*std_valueupper_bound = mean_value+3*std_valuerule = (data_df[column] < lower_bound) | (data_df[column] > upper_bound) # 位于(u-3std,u+3std)区间的数据是正常的,不在这个区间的数据为异常的out = data_df[column].index[rule]# print("异常索引:", out)out_index += out.tolist() data_df.drop(out_index, inplace=True)return data_df
上面的代码做了单列数据的异常剔除,如果需要多列异常剔除,需要对代码进行改写。
4、优缺点
4.1、3σ原则的优点
1.简单易懂:3σ原则基于标准差的观念,提供了一个直观且易于理解的判断标准。通过计算数据的平均值和标准差,并与3σ进行比较,可以快速判断数据是否处于正常范围内。
2.科学性和客观性:由于3σ原则基于统计学原理,其判断具有一定的科学性和客观性。它依赖于数据的统计特性,而不是主观的、经验性的判断。
3.有效检测异常值:根据正态分布的特性,大约有99.73%的数据落在u±3σ范围内。因此,当一个数据点落在这一范围之外时,可以初步判断为异常值。
4.2、3σ原则的缺点
1.对样本量的依赖:3σ原则的有效性依赖于样本量的大小。当样本量较小时,使用3σ原则进行异常值检测可能不够可靠。因为小样本数据可能无法准确反映总体的分布特性。
2.对非正态分布数据的限制:3σ原则主要适用于具有正态分布或近似正态分布特性的数据。对于非正态分布的数据,3σ原则可能无法有效检测异常值,甚至可能出现误判。
写在最后
在实际的数据挖掘项目中,请结合自身数据情况,酌情使用3σ原则。
参考资料
[1]https://zhuanlan.zhihu.com/p/572327280?utm_id=0
[2]https://zhidao.baidu.com/question/585044313.html
[3]https://www.sohu.com/a/365218206_387904
[4]https://blog.csdn.net/Jormungand_V/article/details/109775367
[5]https://blog.51cto.com/u_15834745/6011865
[6]https://www.cnblogs.com/Tree0108/p/12116099.html

请扫码关注下方的公众号,让我们共同进步吧。

相关文章:

【数据挖掘】3σ原则识别数据中的异常值(附代码)
写在前面: 首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 路虽远,行则将至&#…...

人眼是如何看到物体的
我在试图理解人眼如何观察到物体的,发现没有解释。本来我想这应该跟照相机照相的结果一样,但是发现,照相机也不对劲,没有理由能成像啊。 因为物体在散射光的时候,假设散射的光在局部是平行光,那么物体散射…...
vue打包时报错文件包过大
1.问题:npm run build 之后出现 2. 翻译之后意思就是某块过大 3. 解决办法:在vite.config.ts文件上添加 build: { chunkSizeWarningLimit: 1600, }, 4.最终打包...

预编码算法(个人总结)
引言 预编码算法是现代无线通信系统中的关键技术,特别是在多输入多输出(MIMO)系统中。它们通过在发送端对信号进行处理,减少干扰并提高信道容量。这种技术广泛应用于5G、Wi-Fi和卫星通信系统中。本教程将详细介绍预编码算法的背景…...

【重学C语言】十七、预处理指令
【重学C语言】十七、预处理指令 预处理指令预定义宏`#define` 宏定义示例注意事项特殊符号条件编译头文件包含`#pragma`预处理指令 C语言中的预处理指令(Preprocessor Directives)是一种特殊的指令,它们在编译过程的早期阶段(即实际编译之前)被预处理器(Preprocessor)处…...

SQL注入的危害和原理
在Web应用开发中,SQL注入是一种常见的安全漏洞,它允许攻击者通过注入恶意的SQL语句来执行非法操作,甚至获取敏感数据。本篇博客将详细解释SQL注入的危害和原理,并提供一些解决方案,以帮助新人快速理解并避免这种安全威…...
Unity2D横版摄像机跟随
在Unity2D横版游戏中,摄像机跟随是一个非常重要的功能。一个流畅的摄像机跟随系统可以让玩家更好地沉浸在游戏世界中。本文将介绍如何在Unity中实现2D横版摄像机跟随,并分享一些优化技巧。 一、准备工作 在开始实现摄像机跟随之前,请确保您…...

Practicing Version Control
Part A 新建一个文件夹Git,然后进入文件夹: Windows: 在这个文件夹中右键 > Open Git Bash hereMac: 运行终端,打cd 空格,然后将文件夹拖入终端,按 return 从 Github 上复制 HTTPS,然后 git clone https://githu…...
新宏观范式和产业趋势下,纷享销客如何助力企业出海?
出海,已不再是企业的“备胎”,而是必须面对的“大考”!在这个全球化的大潮中,有的企业乘风破浪,勇攀高峰,也有的企业在异国他乡遭遇了“水土不服”。 面对“要么出海,要么出局”的抉择ÿ…...

安装zookeeper
一、搭建前准备 192.168.1.99 sdw1 192.168.1.98 sdw2 192.168.1.97 sdw3 二、搭建 1、各主机修改/etc/hosts,/etc/hostname文件 /etc/hosts 127.0.0.1 localhost localhost.localdomain localhost4 localhost4.localdomain4 ::1 localhos…...

深入分析 Android Activity (二)
文章目录 深入分析 Android Activity (二)1. Activity 的启动模式(Launch Modes)1.1 标准模式(standard)1.2 单顶模式(singleTop)1.3 单任务模式(singleTask)1.4 单实例模式…...
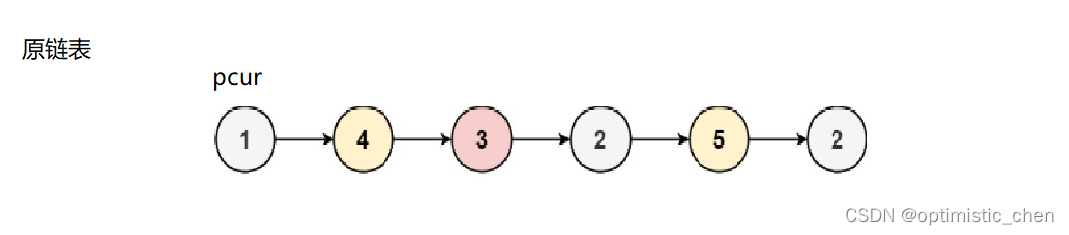
数据结构——经典链表OJ(二)
乐观学习,乐观生活,才能不断前进啊!!! 我的主页:optimistic_chen 我的专栏:c语言 点击主页:optimistic_chen和专栏:c语言, 创作不易,大佬们点赞鼓…...

文件IO(三)
文件IO(三) 左移右移Linux的man 手册文件IO打开文件操作文件关闭文件 caps lock开灯关灯读取按键文件IO操作目录文件打开目录文件操作目录文件 库动态库和静态库的优缺点创建静态库创建动态库 按下右ctrl键 亮灭灯 左移右移 Linux的man 手册 文件IO 打开…...
单实例11.2.0.3迁移到RAC11.2.0.4_使用RMAN 异机恢复
保命法则:先备份再操作,磁盘空间紧张无法备份就让满足,给自己留退路。 场景说明: 1.本文档的环境为同平台、不同版本(操作系统版本可以不同,数据库小版本不同),源机器和目标机器部…...

JavaScript第四讲:函数,作用域,运算符
前言 在JavaScript的广阔天地中,函数、作用域、算术运算符和逻辑运算符是构成代码世界的基石。它们各自扮演着不同的角色,却又紧密相连,共同编织出丰富多彩的程序逻辑。无论是编写一个简单的网页交互,还是构建一个复杂的应用程序…...
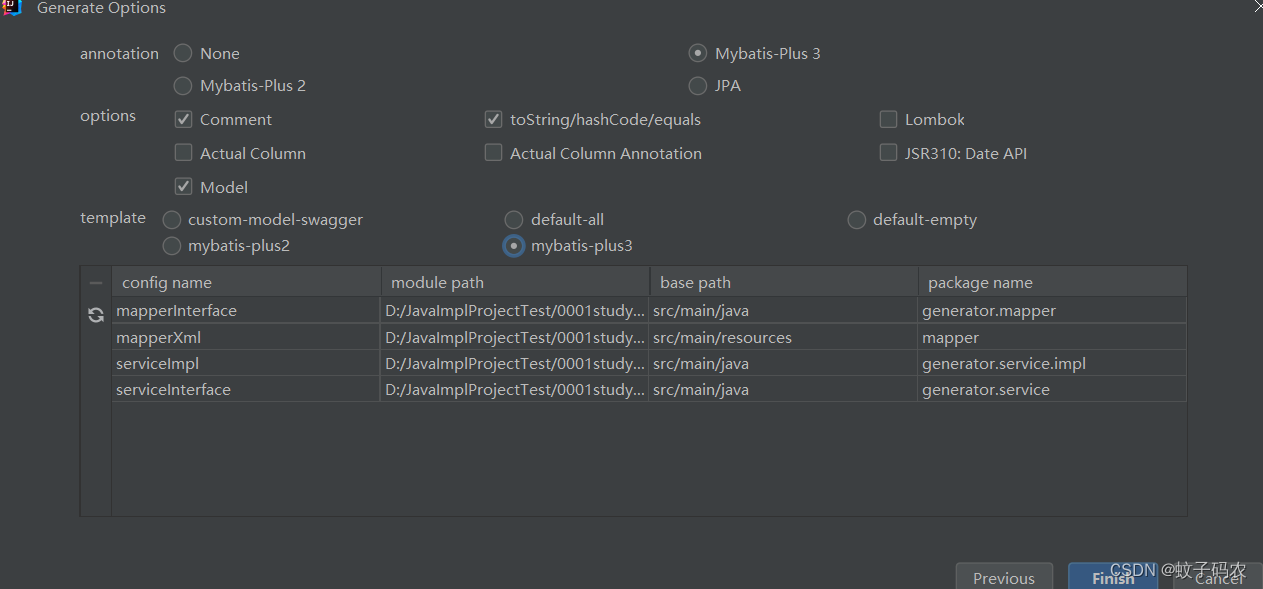
IDEA中,MybatisPlus整合Spring项目的基础用法
一、本文涉及的知识点【重点】 IDEA中使用MybatisPlus生成代码,并使用。 Spring整合了Mybatis框架后,开发变得方便了很多,然而,Mapper、Service和XML文件,在Spring开发中常常会重复地使用,每一次的创建、修…...

从不同角度看如何让大模型变得更聪明呢?
算法创新,从代码上优化大模型,可以采取一系列策略来提升其性能和效率。 算法优化:对模型的算法进行精细调整,如改进神经网络架构,使用更高效的层(如深度可分离卷积),或者优化递归神经…...

Buffer Pool运行机制理解
Buffer Pool机制理解 一、为什么使用Buffer Pool? 众所周知,磁盘数据是以数据页的形式来去读取的,一个数据页默认大小 16K,也就是说你本意只想读取一行数据,但是它会给你加载一页的数据到buffer pool里面。这样的话就…...
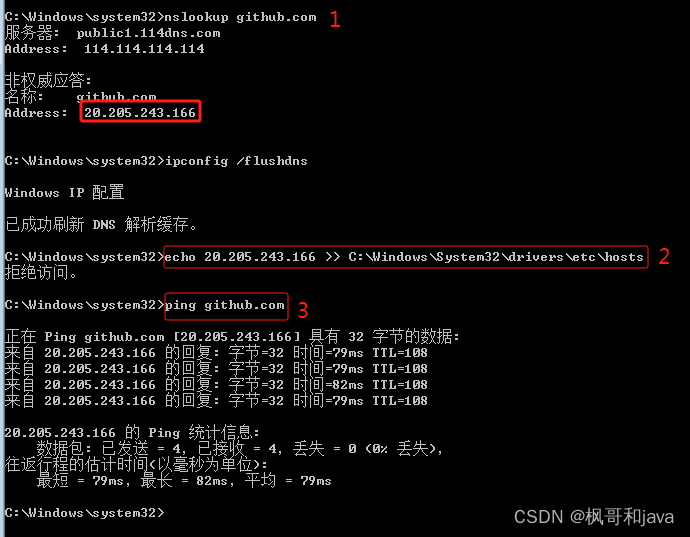
windows配置dns访问git , 加快访问速度保姆级教程
设置 DNS 访问 Git 需要修改电脑的 DNS 配置。下面是具体的操作流程: 第一步:打开命令提示符或终端窗口 在 Windows 系统中,可以按下 Win R 组合键,然后输入 “cmd”,按下 Enter 键打开命令提示符窗口。在 macOS 或 …...

Solidity学习-投票合约示例
以下的合约有一些复杂,但展示了很多Solidity的语言特性。它实现了一个投票合约。 当然,电子投票的主要问题是如何将投票权分配给正确的人员以及如何防止被操纵。 我们不会在这里解决所有的问题,但至少我们会展示如何进行委托投票,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
