LeetCode题练习与总结:路径总和Ⅱ--113
一、题目描述
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
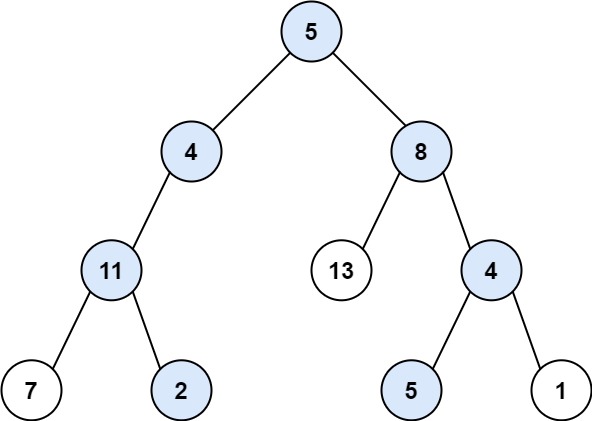
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
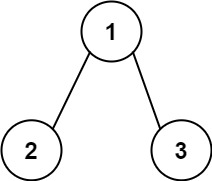
输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
输入:root = [1,2], targetSum = 0 输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
二、解题思路
这个问题可以通过递归的方式解决。我们定义一个递归函数,该函数接受当前节点和当前路径和作为参数。递归函数的工作流程如下:
1. 如果当前节点是空,返回一个空列表。
2. 如果当前节点是叶子节点(即没有子节点),检查当前路径和是否等于目标值。如果是,将当前路径和加入到结果列表中。
3. 如果当前节点不是叶子节点,递归地调用函数:
- 调用函数,参数是当前节点的左子节点和当前路径和加上当前节点的值。
- 调用函数,参数是当前节点的右子节点和当前路径和加上当前节点的值。
4. 将两个递归调用中的结果合并到一起,并返回。
三、具体代码
class Solution {public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> result = new ArrayList<>();if (root == null) {return result;}pathSum(root, targetSum, new ArrayList<>(), result);return result;}private void pathSum(TreeNode node, int target, List<Integer> currentPath, List<List<Integer>> result) {if (node == null) {return;}currentPath.add(node.val);if (node.left == null && node.right == null && target == node.val) {result.add(new ArrayList<>(currentPath));}pathSum(node.left, target - node.val, currentPath, result);pathSum(node.right, target - node.val, currentPath, result);currentPath.remove(currentPath.size() - 1);}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
-
递归函数调用次数:对于每个节点,我们最多会调用一次
pathSum函数。因此,对于一个有 n 个节点的树,最坏情况下,函数会被调用 n 次。 -
单次递归调用的时间复杂度:对于每个节点的单次递归调用,我们需要执行常数时间操作,如判断当前节点是否为空、更新当前路径、判断是否为叶子节点以及添加结果等。
- 综上所述,总的时间复杂度是 O(n),其中 n 是树中节点的数量。
2. 空间复杂度
-
递归调用栈:递归调用会使用系统栈来存储每一层递归的信息。在最坏的情况下,树可能是一个完全二叉树,此时递归调用栈的深度为 O(h),其中 h 是树的高度。
-
其他空间:除了递归调用栈之外,我们不需要额外的空间来存储节点的信息,因此这部分的空间复杂度是 O(1)。
- 综上所述,总的空间复杂度是 O(h),在最坏情况下是 O(n)。
五、总结知识点
-
递归函数:
pathSum函数是一个递归函数,它接受当前节点、目标和当前路径作为参数,并递归地检查左子树和右子树。 -
二叉树的遍历:通过递归的方式,代码实现了对二叉树的遍历,从根节点开始,逐层向下,直到到达叶子节点。
-
路径和的概念:代码中维护了一个变量
currentPath,用于跟踪从根节点到当前节点的路径上所有节点值之和。 -
叶子节点的判断:通过检查当前节点的左右子节点是否都为空来确定一个节点是否是叶子节点。
-
条件语句:代码中使用了
if条件语句来判断节点是否为空、是否为叶子节点以及路径和是否等于目标值。 -
递归终止条件:递归函数在遇到空节点时返回,这是递归的终止条件。
-
逻辑运算符:代码中使用了逻辑运算符
||来组合两个递归调用,如果任意一个调用返回 true,则整个表达式返回 true。 -
函数的封装:
pathSum函数被定义为private,这意味着它只能在同一个类中被访问,这是封装的一种形式。 -
树的表示:代码中使用了
TreeNode类来定义二叉树的节点,这是二叉树数据结构的基本表示方法。 -
列表的使用:代码中使用了
ArrayList类来存储路径和结果,这是一种动态数组,可以方便地添加和删除元素。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:路径总和Ⅱ--113
一、题目描述 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [5,4,8,11,null,13,4,7,2,null,null,5,1], target…...

Java复数计算
复数在数学、科学或者工程领域是很常用的,可以通过调用Apache Commons Math库来完成,也可以自己手撸。 一、使用Apache Commons Math库 这个库有多个版本,在写这篇文章时,它的最新版是2022年12月19日的4.0-beta1,构建…...
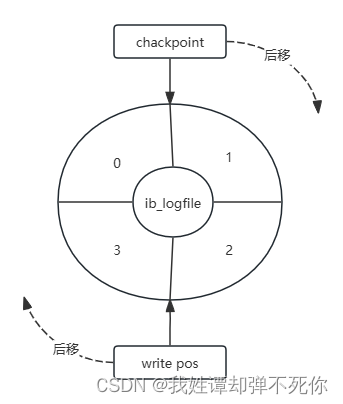
MySQL-事务日志
事务的隔离性由 锁机制 实现 事务的原子性、一致性、隔离性 由事务的 redo日志 和 undo 日志来保证 redo log 称为 重做日志,提供再写入操作,恢复提交事务修改的页操作,用来保证事务的持久性。undo log 称为 回滚日志,回滚行记录…...
)
PySide6 GUI 学习笔记——常用类及控件使用方法(常用类坐标点QPoint)
控件是PySide设计好的能承载用户输入、输出的小窗体,将多个控件有机整合,能形成用户所需要的界面。而每一个控件,都有属于自己的属性、方法、信号、槽函数和事件(event),且控件与控件之间又有继承关系。 G…...
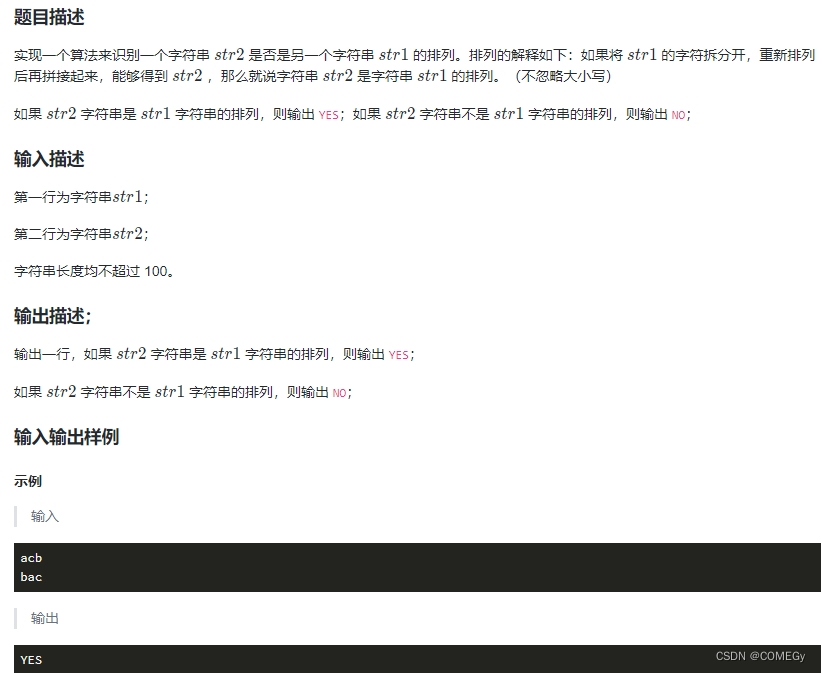
算法练习——字符串
一确定字符串是否包含唯一字符 1.1涉及知识点 c的输入输出语法 cin>>s; cout<<"NO"; 如何定义字符串 切记:在[]中必须加数字——字符串最大长度,不然编译不通过 char s[101]; 如何获取字符串长度 char s[101];cin>>s;i…...

Flutter 中的 SliverOverlapInjector 小部件:全面指南
Flutter 中的 SliverOverlapInjector 小部件:全面指南 Flutter 是一个功能丰富的 UI 框架,由 Google 开发,允许开发者使用 Dart 语言构建跨平台的移动、Web 和桌面应用。在 Flutter 的滚动视图系统中,SliverOverlapInjector 是一…...

7个Python爬虫入门小案例
大家好,随着互联网的快速发展,数据成为了新时代的石油。Python作为一种高效、易学的编程语言,在数据采集领域有着广泛的应用。本文将详细讲解Python爬虫的原理、常用库以及实战案例,帮助读者掌握爬虫技能。 一、爬虫原理 爬虫&a…...
 构造数字)
linux 利用 ~$() 构造数字
2024.6.1 题目 <?php //flag in 12.php error_reporting(0); if(isset($_GET[x])){$x $_GET[x];if(!preg_match("/[a-z0-9;|#\"%&\x09\x0a><.,?*\-\\[\]]/i", $x)){system("cat ".$x.".php");} }else{highlight_file(__F…...
七大获取免费https的方式
想要实现https访问最简单有效的的方法就是安装SSL证书。只要证书正常安装上以后,浏览器就不会出现网站不安全提示或者访问被拦截的情况。下面我来教大家怎么去获取免费的SSL证书,又如何安装证书实现https访问。 一、选择免费SSL证书提供商 有多家机构提…...

JVM(Java虚拟机)笔记
面试常见: 请你谈谈你对JVM的理解?java8虚拟机和之前的变化更新?什么是OOM,什么是栈溢出StackOverFlowError? 怎么分析?JVM的常用调优参数有哪些?内存快照如何抓取?怎么分析Dump文件?谈谈JVM中,类加载器你的认识…...

秒杀基本功能开发(显示商品列表和商品详情)
文章目录 1.数据库表设计1.商品表2.秒杀商品表3.修改一下秒杀时间为今天到明天 2.pojo和vo编写1.com/sxs/seckill/pojo/Goods.java2.com/sxs/seckill/pojo/SeckillGoods.java3.com/sxs/seckill/vo/GoodsVo.java 3.Mapper编写1.GoodsMapper.java2.GoodsMapper.xml3.分别编写Seck…...

centos 记录用户登陆ip和执行命令
centos 记录用户登陆ip和执行命令 在/etc/profile 文件末尾添加如下代码: #!/bin/bash USER_IPwho -u am i 2>/dev/null | awk {print $NF} | sed -e s/[()]//g HISTDIR/usr/share/.history if [ -z "$USER_IP" ]; then USER_IPhostname fi…...

JZ2440笔记:DM9000C网卡驱动
在厂家提供的dm9dev9000c.c上修改, 1、注释掉#ifdef MODULE #endif 2、用模块化函数修饰入口出口函数 3、在dm9000c_init入口函数,增加iobase (int)ioremap(0x20000000,1024);irq IRQ_EINT7; 4、一路进入,在dmfe_probe1中注释掉if((db…...
【数据结构】二叉树:简约和复杂的交织之美
专栏引入: 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累…...

信号稳定,性能卓越!德思特礁鲨系列MiMo天线正式发布!
作者介绍 礁鲨系列天线,以其独特的外观设计和强大的性能,成为德思特Panorama智能天线家族的最新成员。这款天线不仅稳定提供5G、WIFI和GNSS信号,更能在各类复杂环境中展现出卓越的性能。它的设计灵感来源于海洋中的礁鲨,象征着力量…...

编程学习技巧——实战
目录 学习思路待续、更新中 学习思路 实战大小项目 翻阅官网手册——学习技术,调试问题 待续、更新中 1 顿号、: 先使用ctrl. ,再使用一遍切回 2 下标: 21 2~1~ 3 上标: 2 0 2^{0} 20 $2^{0}$ 4 竖线 | : | ; | 5 空格: &emsp ; 6 换行: &nbs…...

GPU学习(1)
一、为什么要GPU 我们先看一个基本的神经网络计算 YF(x)AxB 这就是一次乘法一次加法 ,也叫FMA,(fused multiply-add) 如果矩阵乘,就是上面的那个式子扩展一下,所以又用了这张老图 比如你要多执行好几个yAxB,可能比较简…...
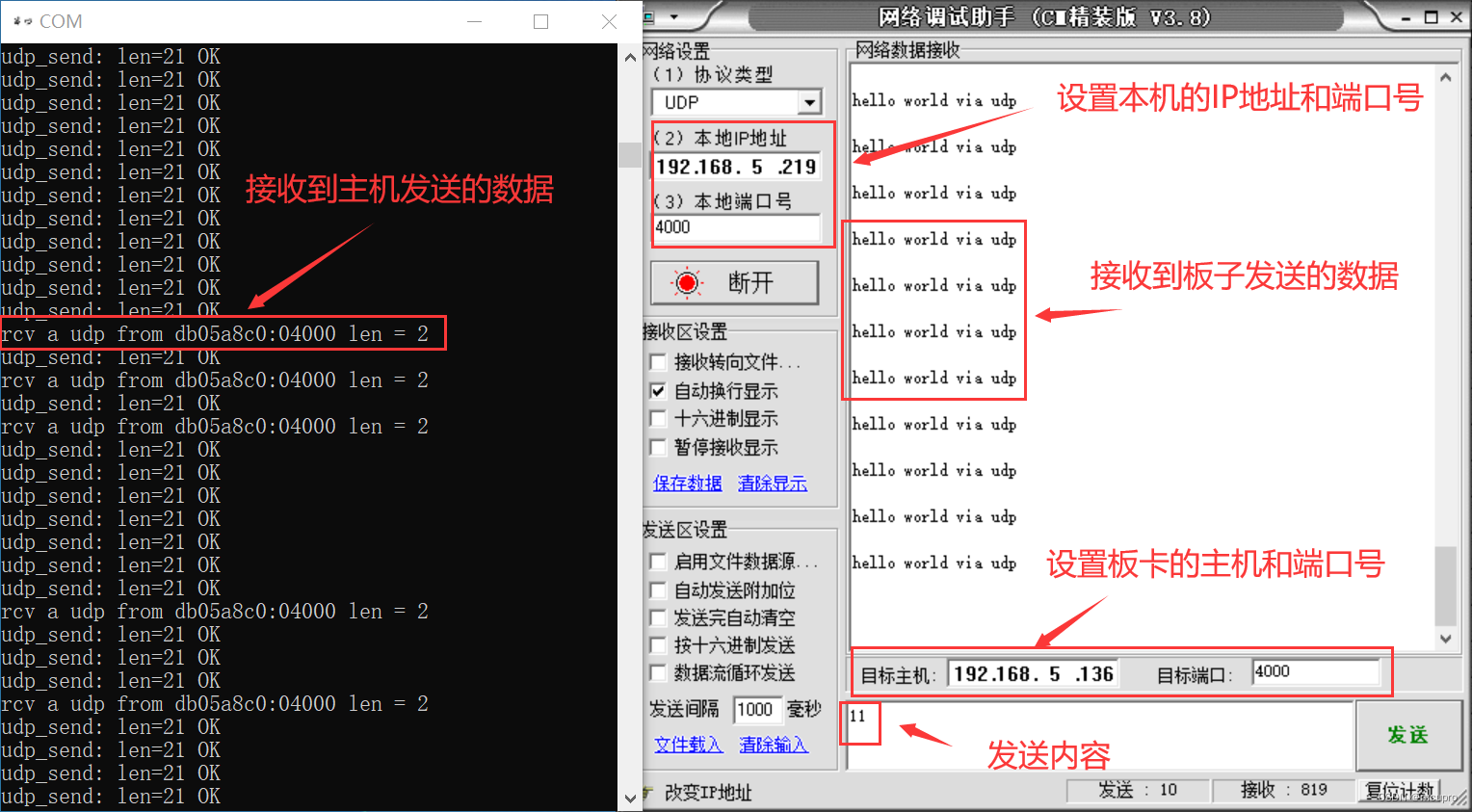
TQSDRPI开发板教程:UDP收发测试
项目资源分享 链接:https://pan.baidu.com/s/1gWNSA9czrGwUYJXdeuOwgQ 提取码:tfo0 LWIP自环教程:https://blog.csdn.net/mcupro/article/details/139350727?spm1001.2014.3001.5501 在lwip自环的基础上修改代码实现UDP的收发测试。新建一…...
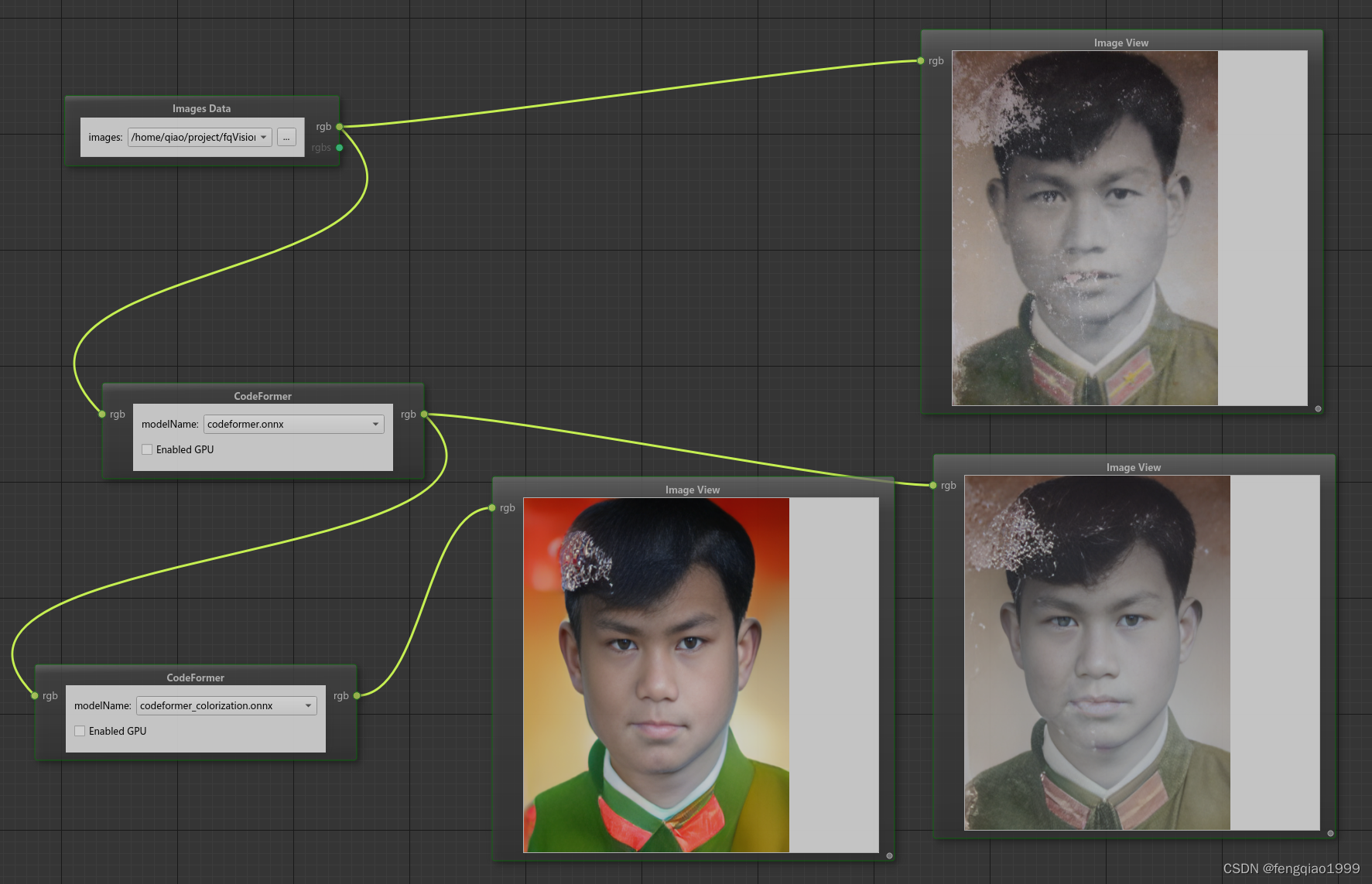
opencv进阶 ——(九)图像处理之人脸修复祛马赛克算法CodeFormer
算法简介 CodeFormer是一种基于AI技术深度学习的人脸复原模型,由南洋理工大学和商汤科技联合研究中心联合开发,它能够接收模糊或马赛克图像作为输入,并生成更清晰的原始图像。算法源码地址:https://github.com/sczhou/CodeFormer…...
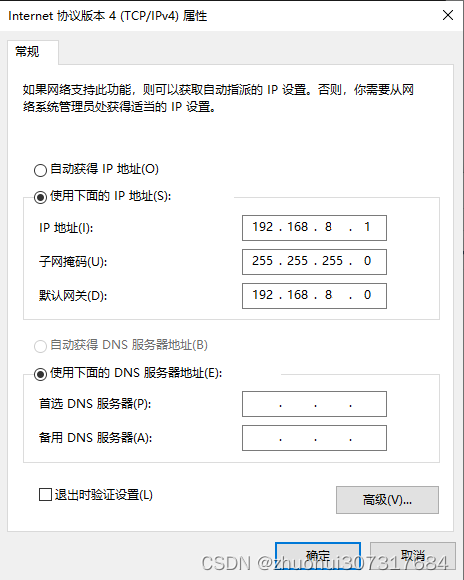
虚拟机改IP地址
使用场景:当你从另一台电脑复制一个VMware虚拟机过来,就是遇到一个问题,虚拟的IP地址不一样(比如,一个是192.168.1.3,另一个是192.168.2.4,由于‘1’和‘2’不同,不是同一网段&#…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
