颠仆流离学二叉树2 (Java篇)
本篇会加入个人的所谓鱼式疯言
❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言
而是理解过并总结出来通俗易懂的大白话,
小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.
🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 !!!

前言
在上篇中我们学习了 二叉树的基本概念 以及他们的特性结论,并运用到了 具体的题目 中去解决问题 。
而在本篇中,小编讲继续学习 二叉树 的基本操作, 主要围绕着我们 遍历二叉树 来讲解 , 人狠话不多,下面让我们切入主题吧 💥 💥 💥
目录
-
二叉树的遍历初识
-
前序遍历
-
中序遍历
4.后序遍历
-
层序遍历
-
二叉树遍历的应用
一. 二叉树的遍历初识
学习二叉树的结构,最简单的方式就是遍历,所谓遍历 是指 沿着某条搜索路线,依次树中的某个节点均做一次访问, 访问节点所做的操作 依赖于要解决的各种实际问题。
遍历是二叉树是最重要的操作之一,是 二叉树上进行其他运算 的基础
1. 二叉树的遍历简介
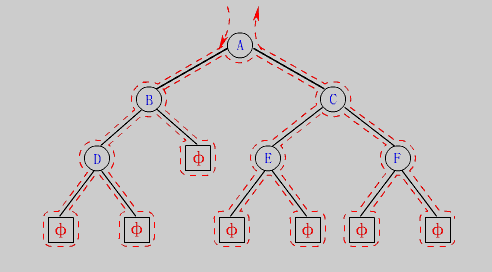
在遍历二叉树时, 如果没有进行某种约定,每个人都按照自己的方式来遍历, 得到的结果就比较乱, 如果我们按照某个规则 来遍历, 则每个人对于遍历结果都是相同的 , 如果 N 代表 根节点,L 代表左节点, R 代表 右节点, 那根据遍历的的节点有以下的遍历方式。
-
NLR: 前序遍历 (先序遍历) 根据
根——》 左 ——》 右的顺序对二叉树进行遍历 -
LNR : ==中序遍历 ==: 根据
左——》 根——》 右的顺序 对二叉树进行遍历 -
LRN 后序遍历 : 根据
左——》 右 ——》 根的顺序对二叉树进行遍历
详细的遍历方式, 小编下面细讲哦 💖 💖 💖 💖
在遍历二叉树之前, 我们先用一下代码简单的 构建一颗二叉树
public class MyBinaryTree {public static class TreeNode {public TreeNode left;public TreeNode right;public char val;public TreeNode(char val) {this.val = val;}}private TreeNode root;// 构造二叉树public TreeNode createBinaryTree() {root=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode H=new TreeNode('H');TreeNode C=new TreeNode('C');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');root.left=B;B.left=D;B.right=E;E.right=H;root.right=C;C.left=F;C.right=G;return root;}// 前序遍历
void preOrder(Node root);
// 中序遍历
void inOrder(Node root);
// 后序遍历
void postOrder(Node root);}
二. 前序遍历
1. 前序遍历的特点
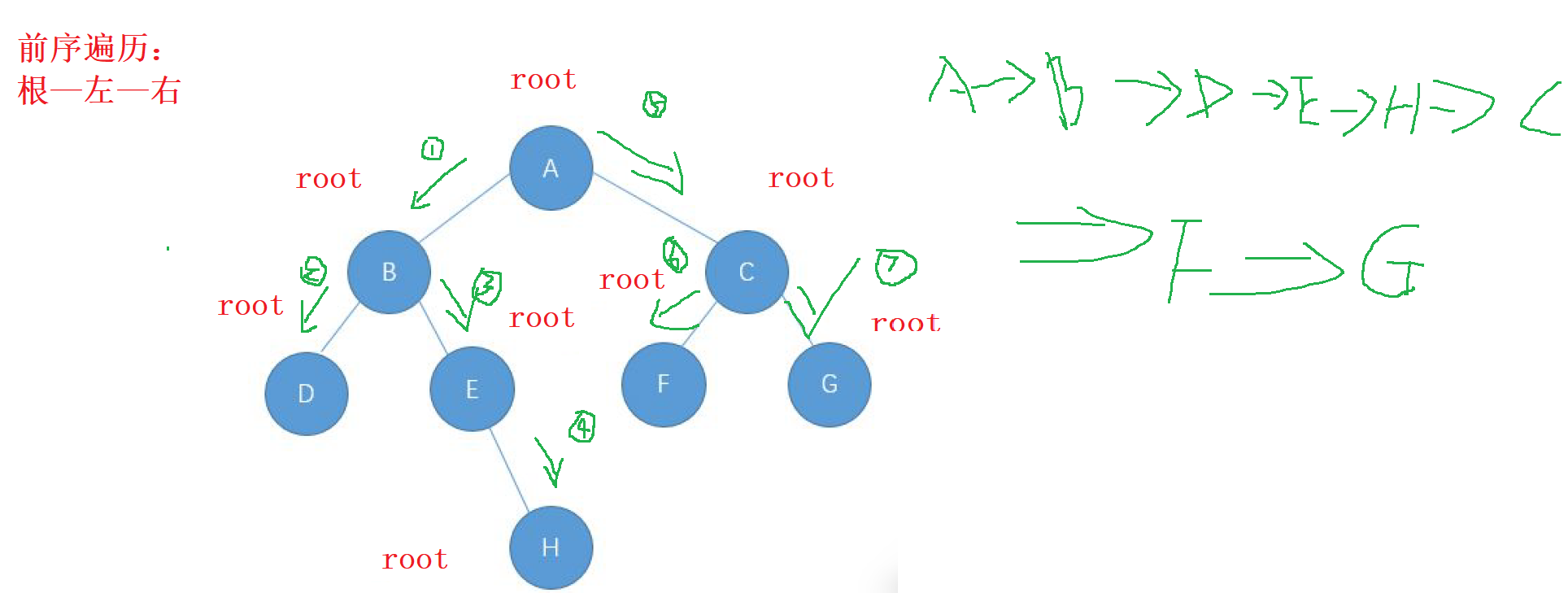
按照从左子树开始走,一直 往下递归,每一步所走的路径成为我们的根,先遍历完根之后。
按照根左右的顺序, 当我们走完每个根节点的左子树 时, 先往下递, 再往
回归, 左节点成为新的根, 会到最初的根节点之后,再向右子树进行先递后归的操作,
动画演示
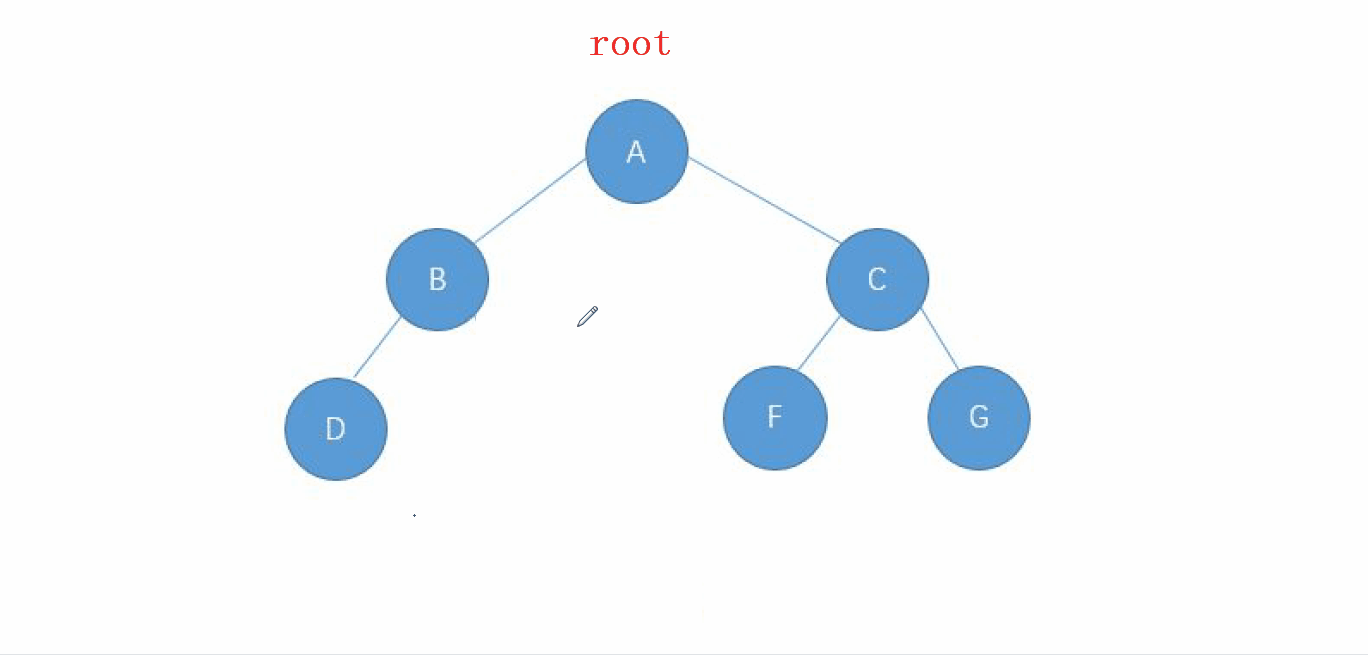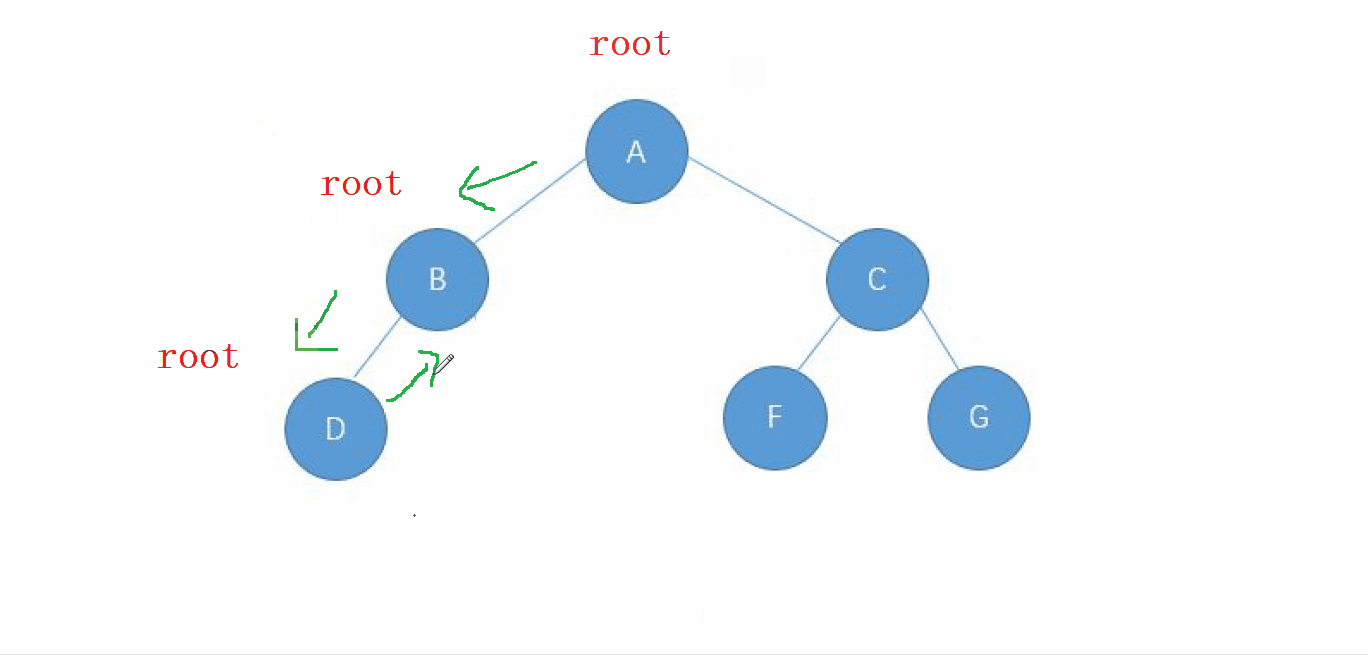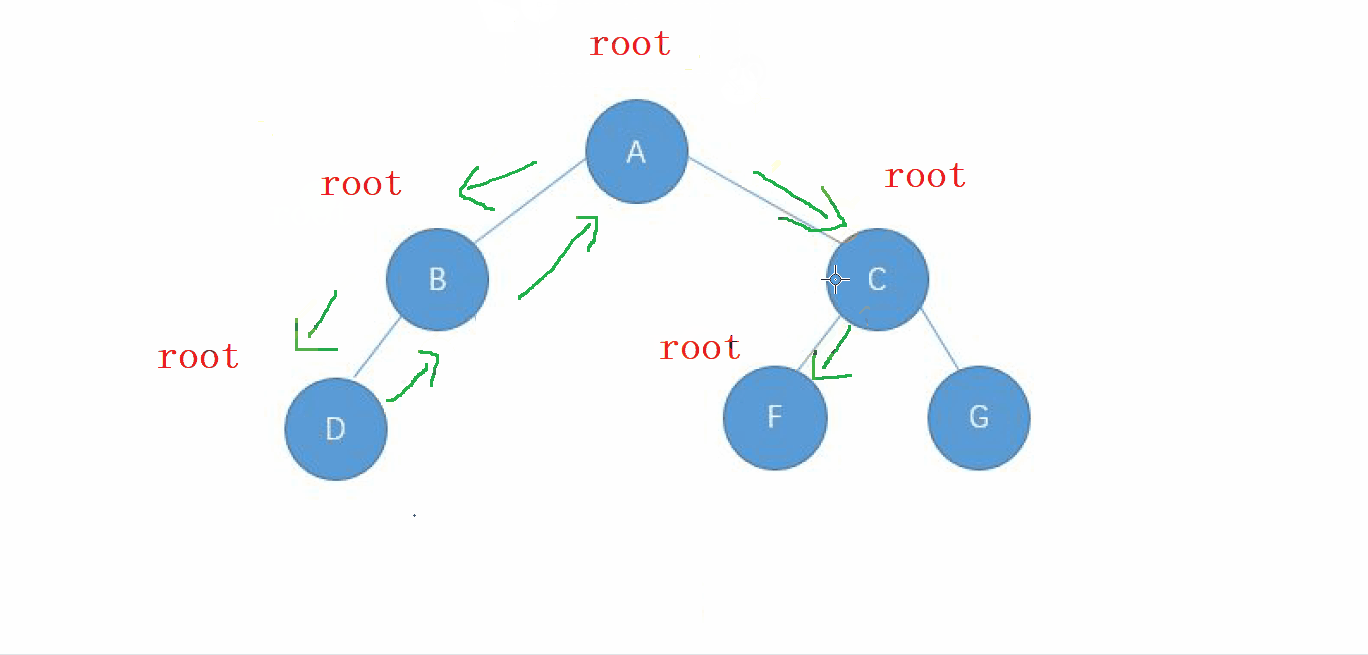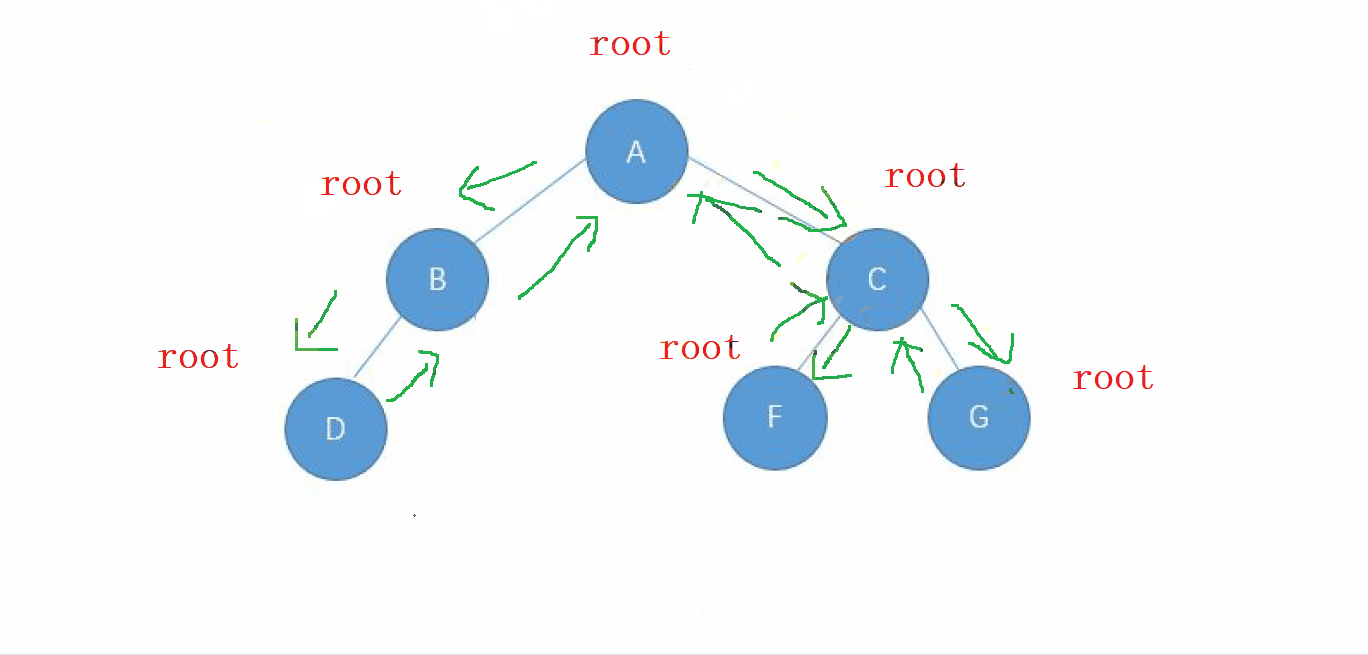
2. 前序遍历的实现
因为前序遍历有 递归 和 非递归 的两种方式, 但 遍历的原理和方向都是一致的
在本篇文章中,。小编都会带着小伙伴们 一 一 实现 💥 💥 💥 💥

<1>. 前序遍历的递归实现
// 前序遍历public void FirstDisplay(TreeNode root) {if (root==null) {return;}System.out.print(root.val+" ");FirstDisplay(root.left);FirstDisplay(root.right);}
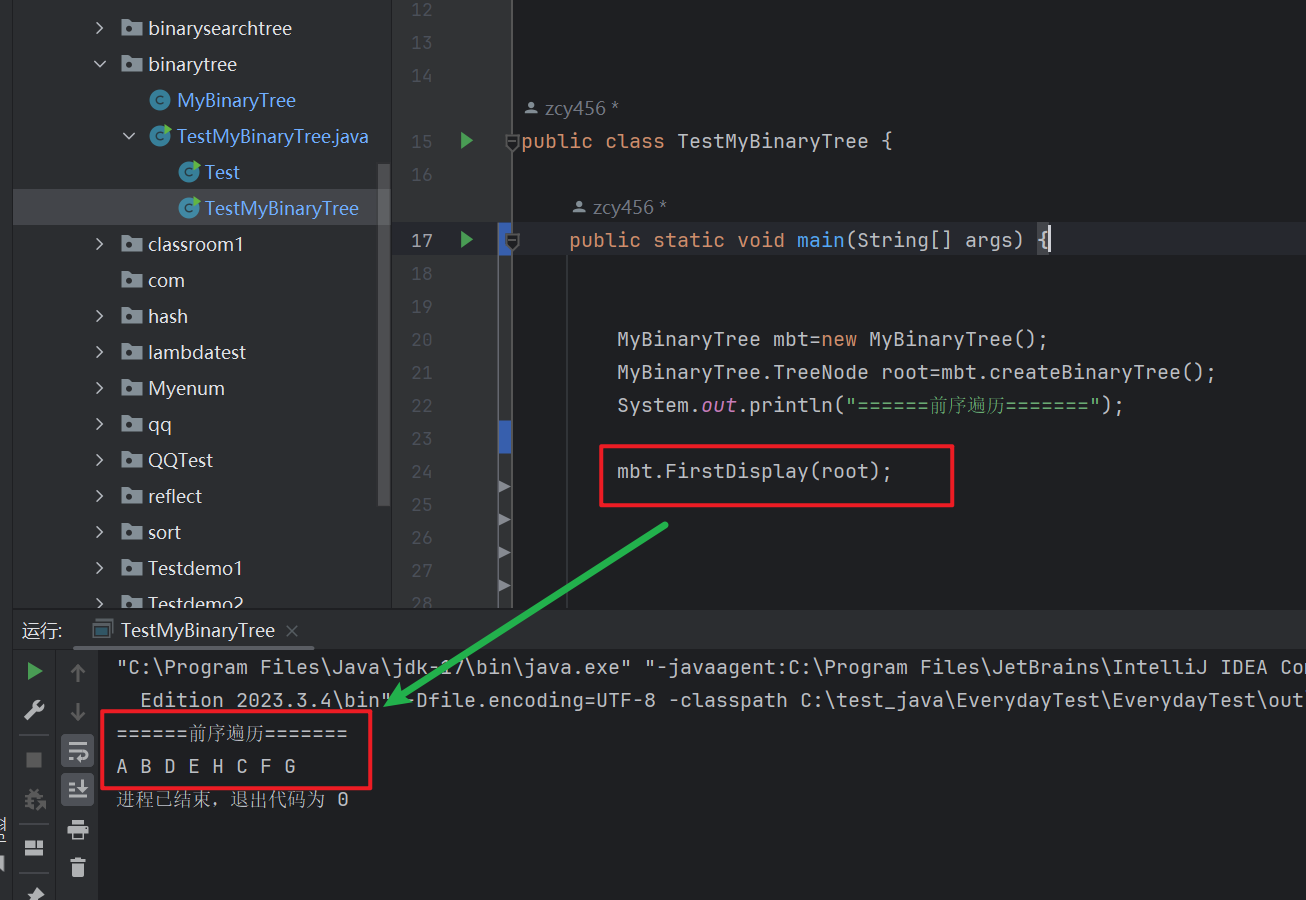
这里的代码的递归思路就是完美的按照我们遍历方向来的,
先访问,后递归
<2>. 前序遍历的非递归实现
// 非递归的前序遍历public void FirstDisplayNo(TreeNode root) {// 先创建一个栈来存放树的每个节点Stack<TreeNode> stack=new Stack<>();// 先把艮节点创建一遍TreeNode cur=root;/*** 外循环主要遍历 右边的节点* 用于出栈的数据* 并让节点向右移动*/while (cur != null || !stack.empty()) {/*** 在这个内循环中* 当往左走就添加数据,一直到为 null 结束* 并进行打印*/while (cur != null) {// 先打印System.out.print(cur.val+" ");// 打印完就入栈stack.add(cur);// 节点向左移动cur=cur.left;}// 出栈存放数据cur=stack.pop();// 并向右走cur=cur.right;// 当再次循环时,如果左边还有节点就会继续存放}System.out.println();}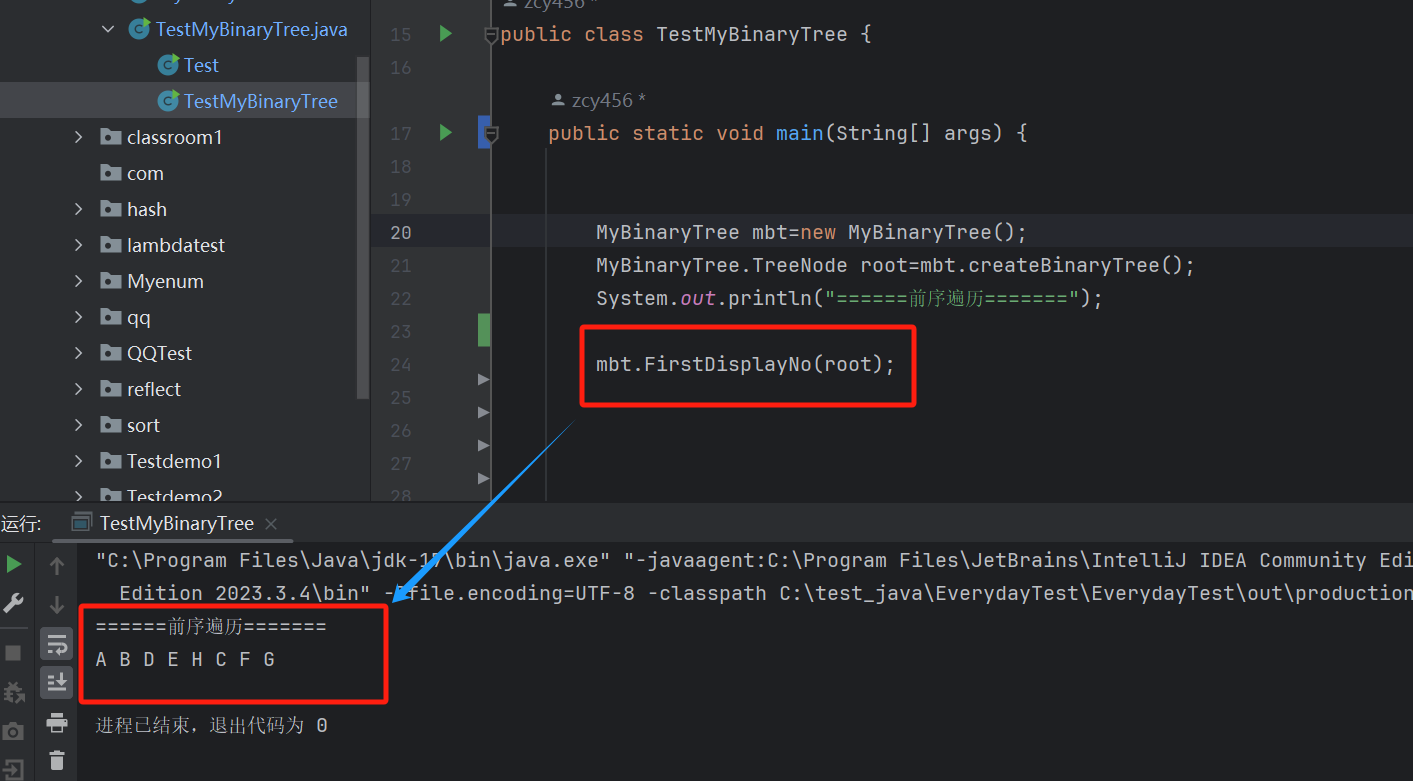
非递归的 实现步骤
- 先定义一个栈 , 来记录我们每次遍历过的
根节点
- 先让根节点一直
向左走,当遍历完我们的 左子树 (也就是我们的root = null时候), 并且入栈, 记录下来以便后面我们遍历右子树
- 然后出栈, 开始
向右走, 遍历我们的右子树
- 当整个栈为
null并且到达的这个节点 cur 也为null, 就意味着遍历完整个 二叉树所有的节点
鱼式疯言
无论是 递归还是非递归的 前序遍历 , 我们的 前序遍历思路就是
先走根 , 根走完走左 , 左走完回到根,
再走右,一层一层的走,一步一步的回。
细节处理:
在代码上我们要注意的就是这个当节点为 null ,也就意味着我们要开始 回退 到 上一个节点
二. 中序遍历
1. 中序遍历的特点
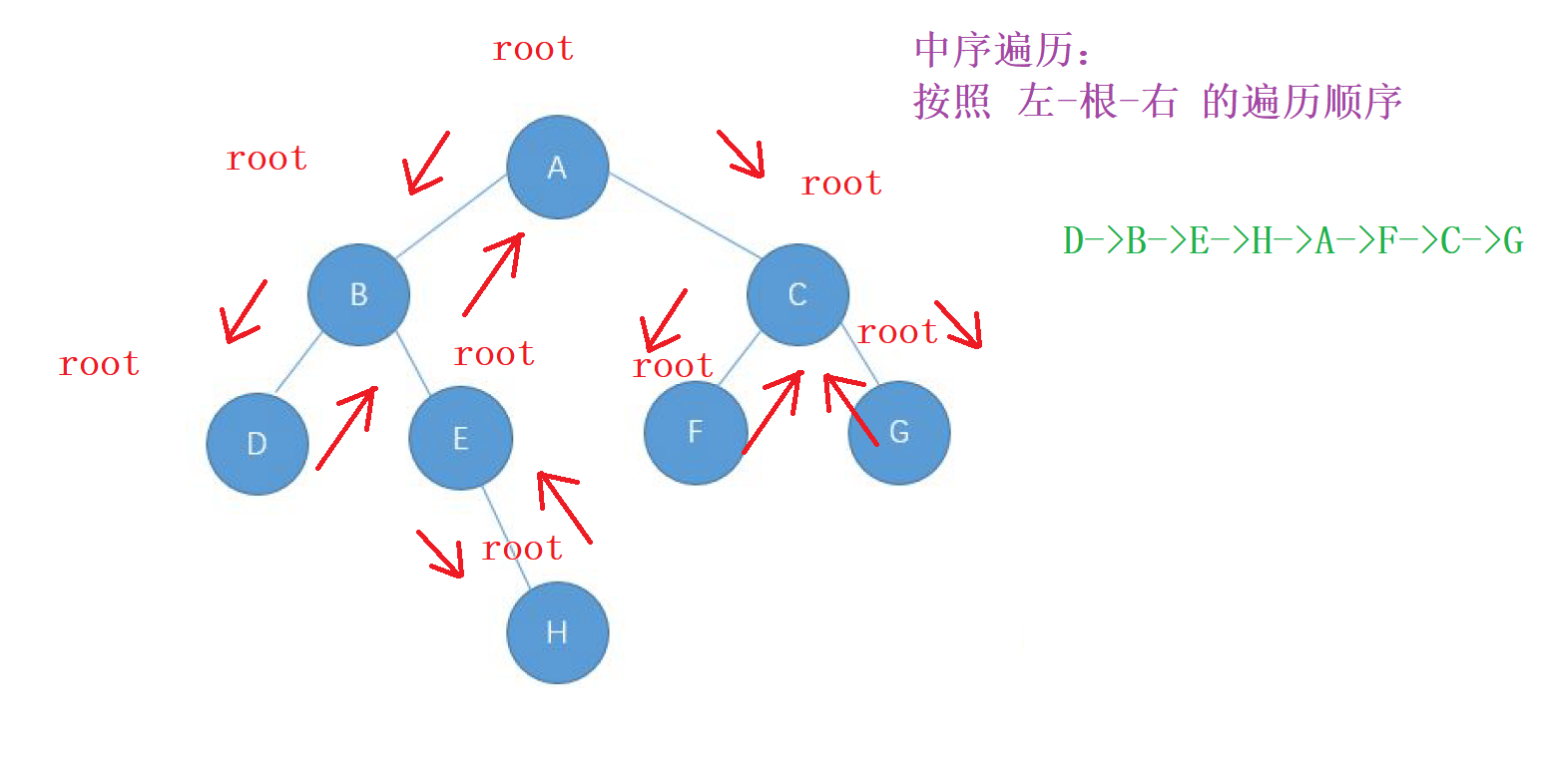
我们知道 中序遍历 , 是以 左- 根-右的顺序 进行遍历
我们先从 走左边, 还是让每个左节点先成为新的根, 当这个新的根的
左子树都走完之后, 才能真正访问我们当前 新的节点。
以此类推,我们新的节点访问结束后,就会进行回退到前一个旧的节点,继续访问,最终当整个 左子树走完 , 并且 访问完我们的根 , 就遍历我们的
右子树,最终回到我们整颗树的根节点
动画演示
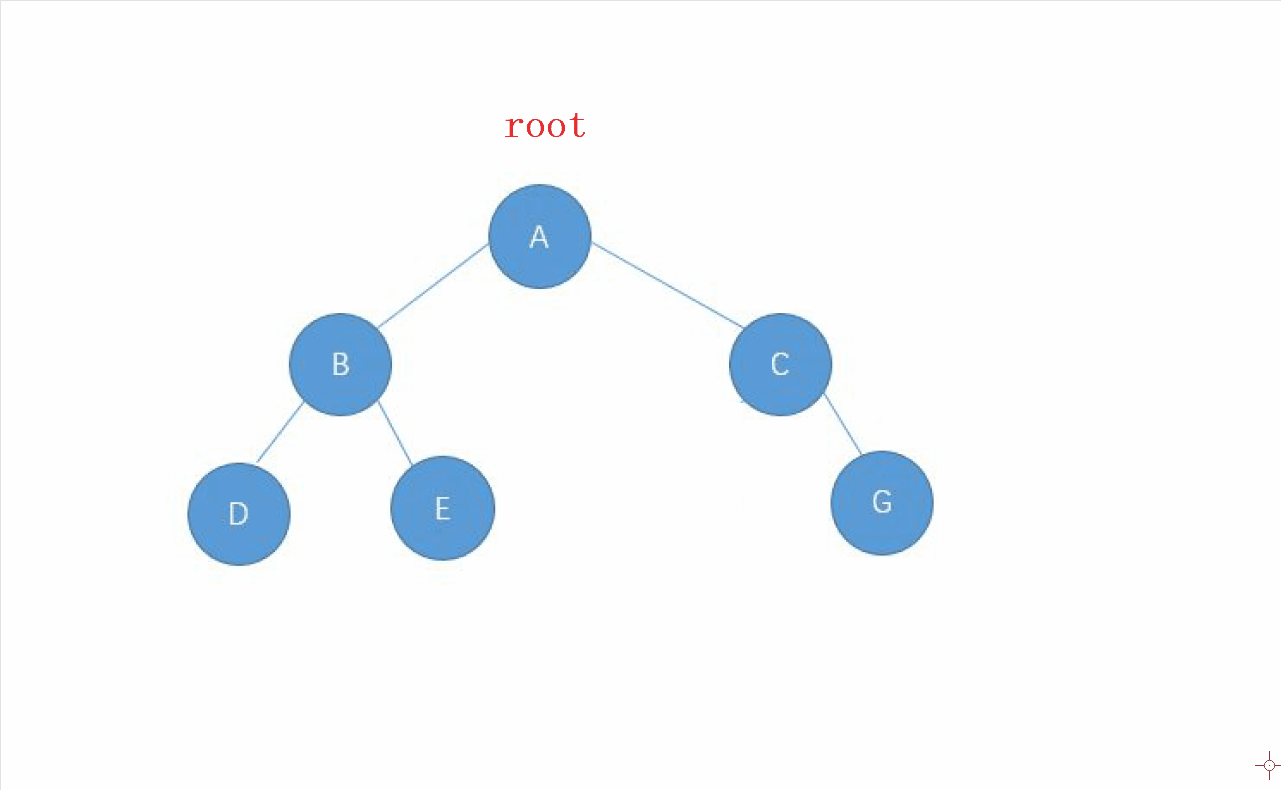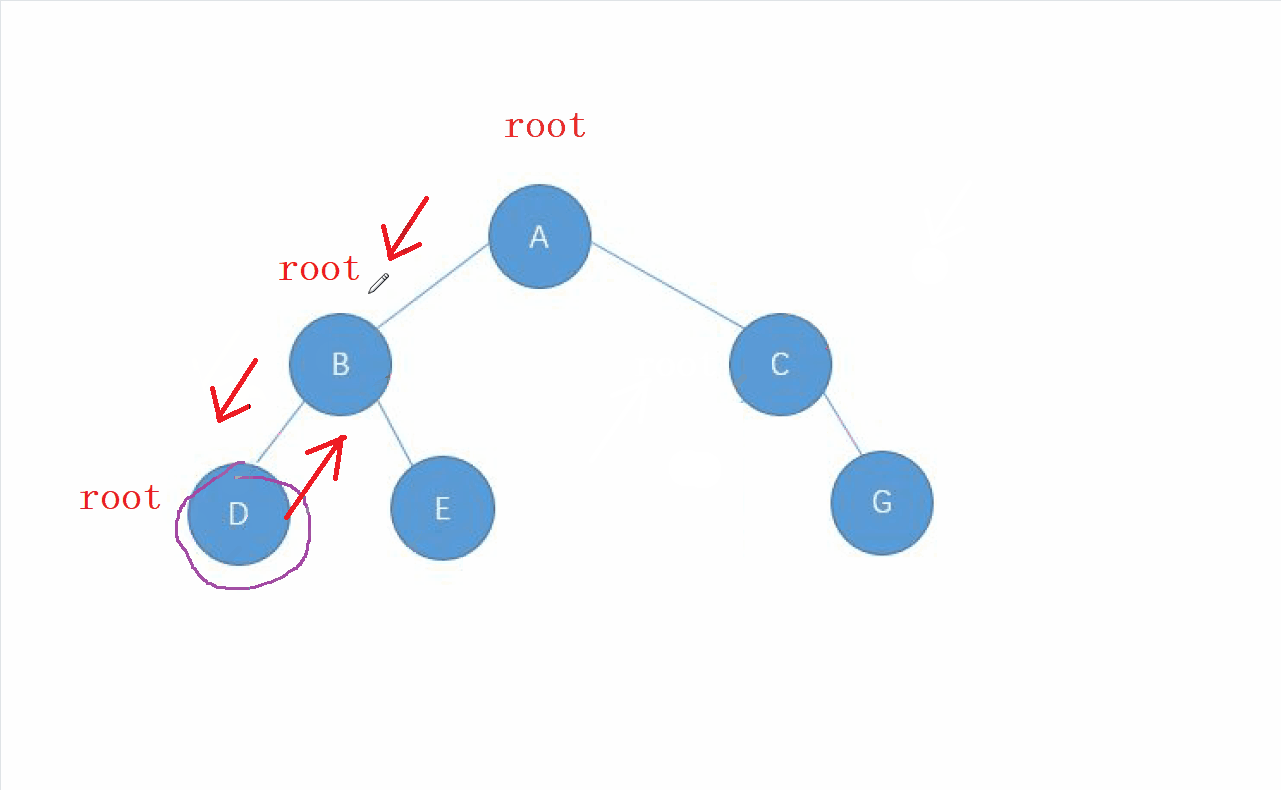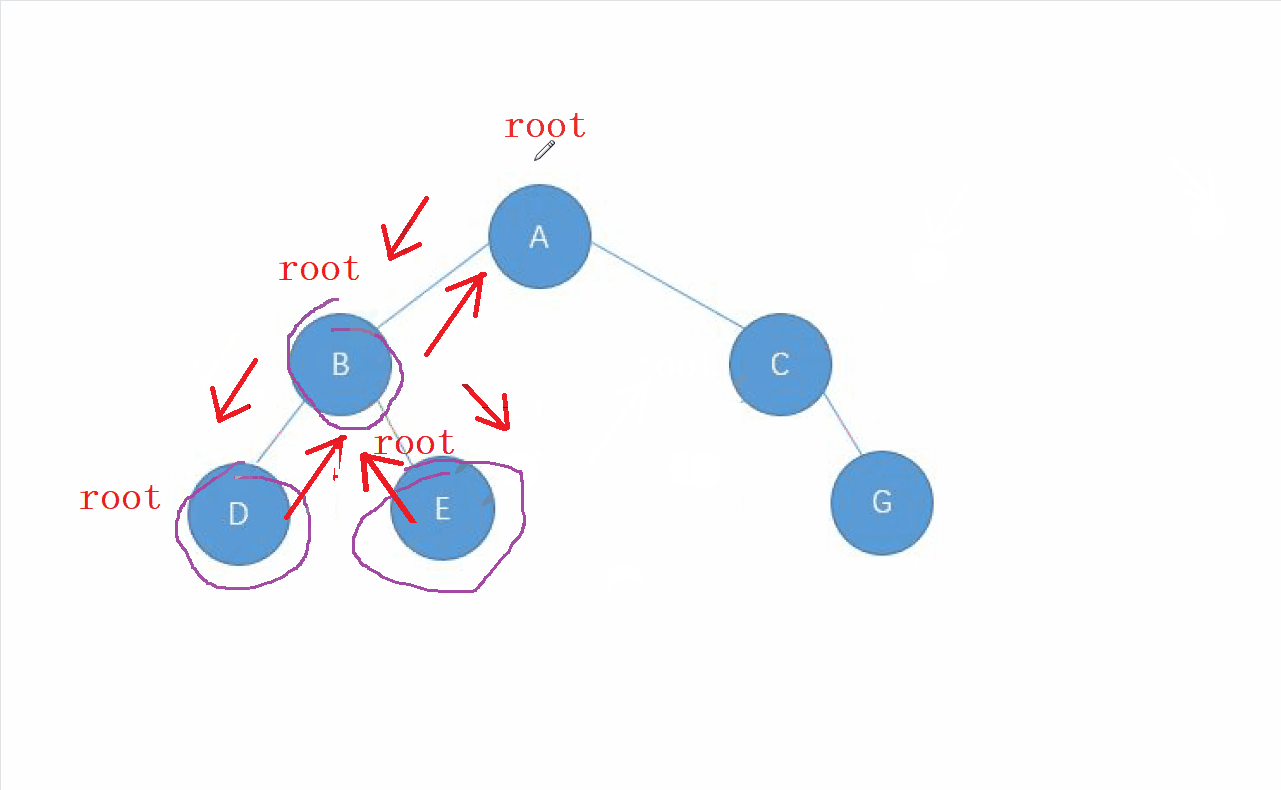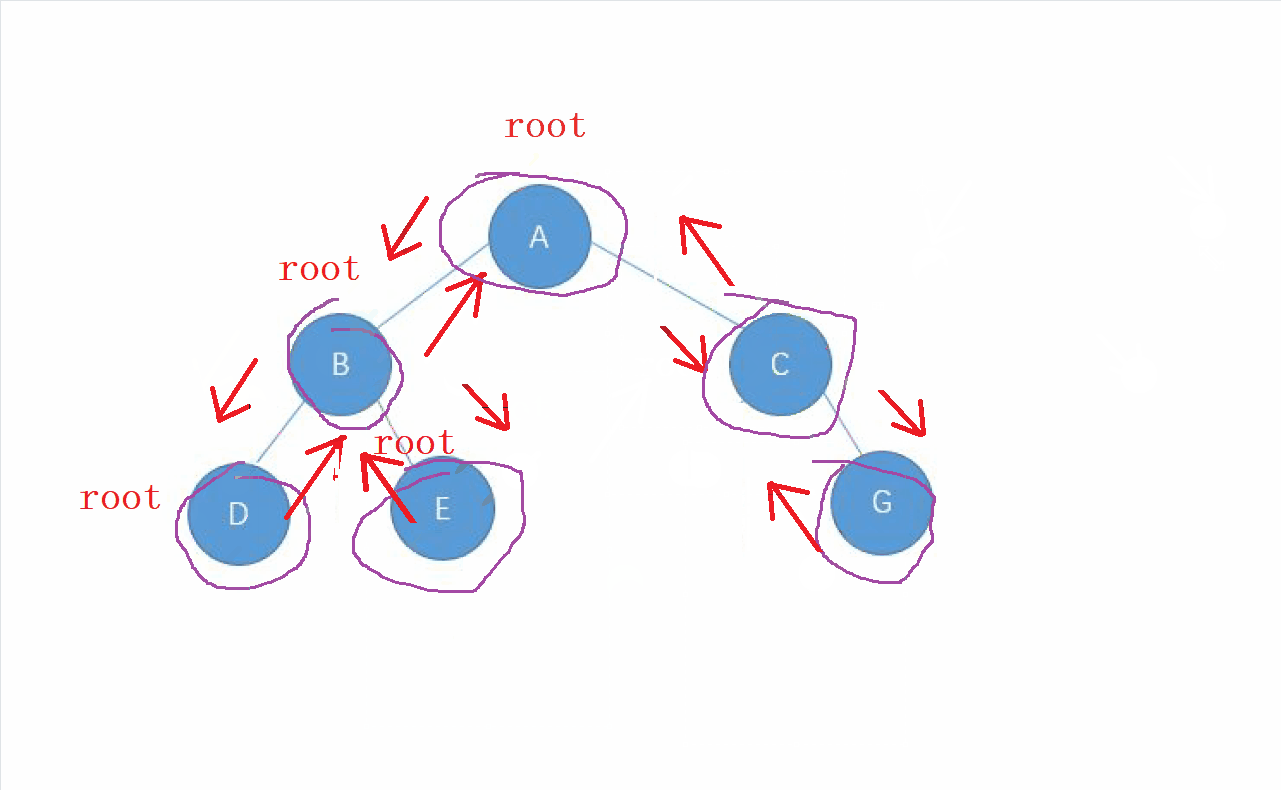
2.中序遍历的实现

<1>.中序遍历的递归实现
// 中序遍历
public void middleDisplay(TreeNode root) {if (root==null) {return;}middleDisplay(root.left);System.out.print(root.val+" ");middleDisplay(root.right);
}
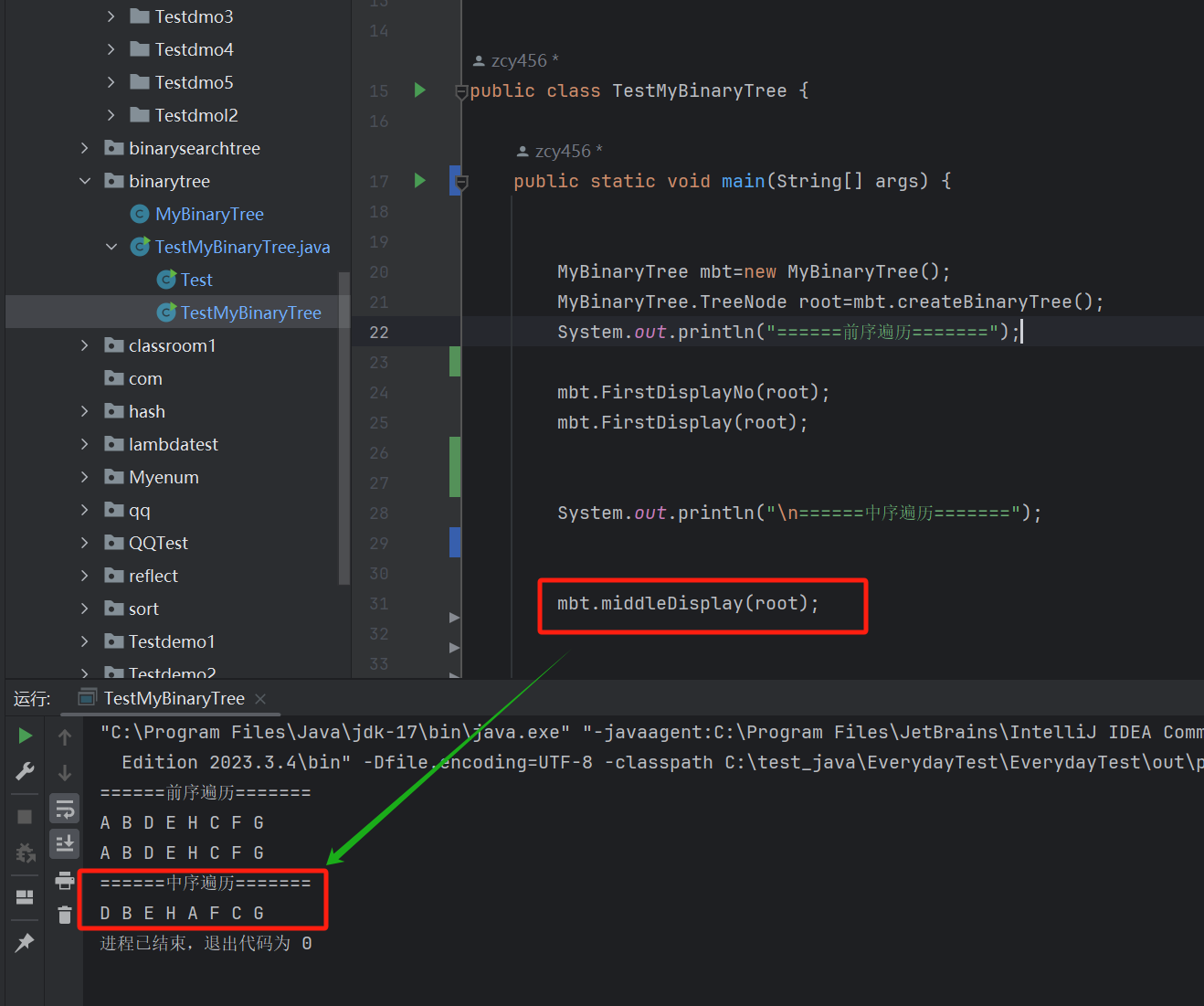
这里的代码的递归思路就是完美的按照我们遍历方向来的,
先递归,后访问,小编在这里就 不赘述 了
<2>. 中序遍历的非递归实现
// 非递归的中序遍历public void middleDisplayNo (TreeNode root) {// 创建一个栈用于回退节点Stack<TreeNode> stack=new Stack<>();// 先放根节点TreeNode cur=root;/*** 外循环主要用于遍历 右边* 更是用于出栈的回退*/while (cur != null || !stack.empty()) {/*** 内循环先遍历下去* 边遍历边存放*/while (cur != null) {stack.add(cur);cur=cur.left;}// 出栈最后一个无左节点的左子树cur=stack.pop();// 打印该节点System.out.print(cur.val+" ");// 再往右走cur=cur.right;}System.out.println();}
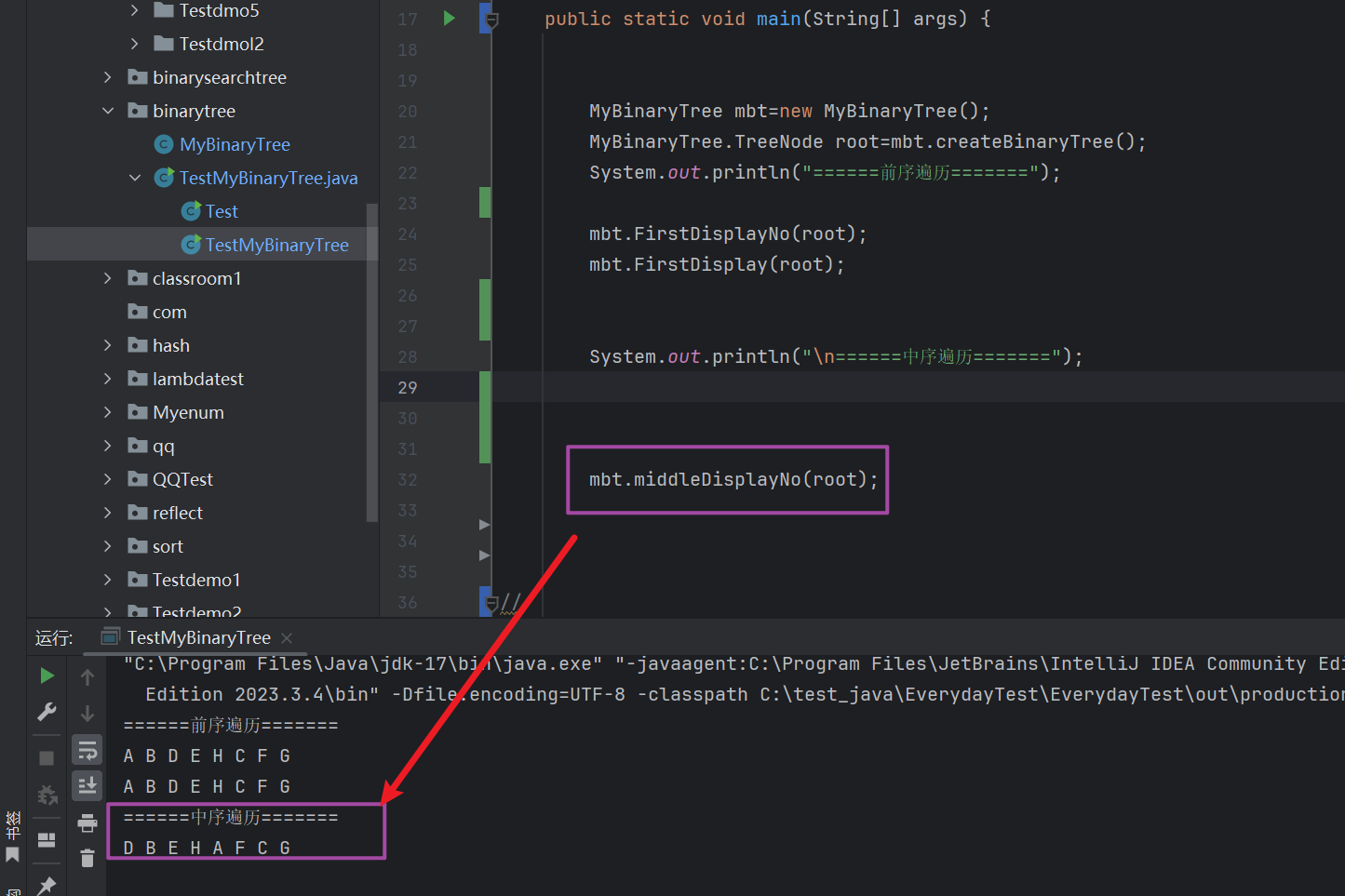
非递归的实现步骤:
我们先定义一个 栈 ,用来存储走过的每个 左子树的节点
-
先
往左边的节点走,先整个左子树的每个节点都入栈, 当 这个节点 为 null 就停止入栈 -
然后进行出栈, 出栈的时候,我们就可以对该节点进行打印(访问) , 并且向
右子树节点开始走 -
当整个栈为
null并且 该节点也为 null , 也就意味着遍历完二叉树所有的节点
鱼式疯言
中序遍历的最核心的要点就是
无论是
递归还是非递归的 中序遍历:
一定要先
走完每个左子树, 当我们进行 回退 的时候。 才轮的到该 根节点去遍历, 最后才走右子树的一种 顺序.
三. 后序遍历
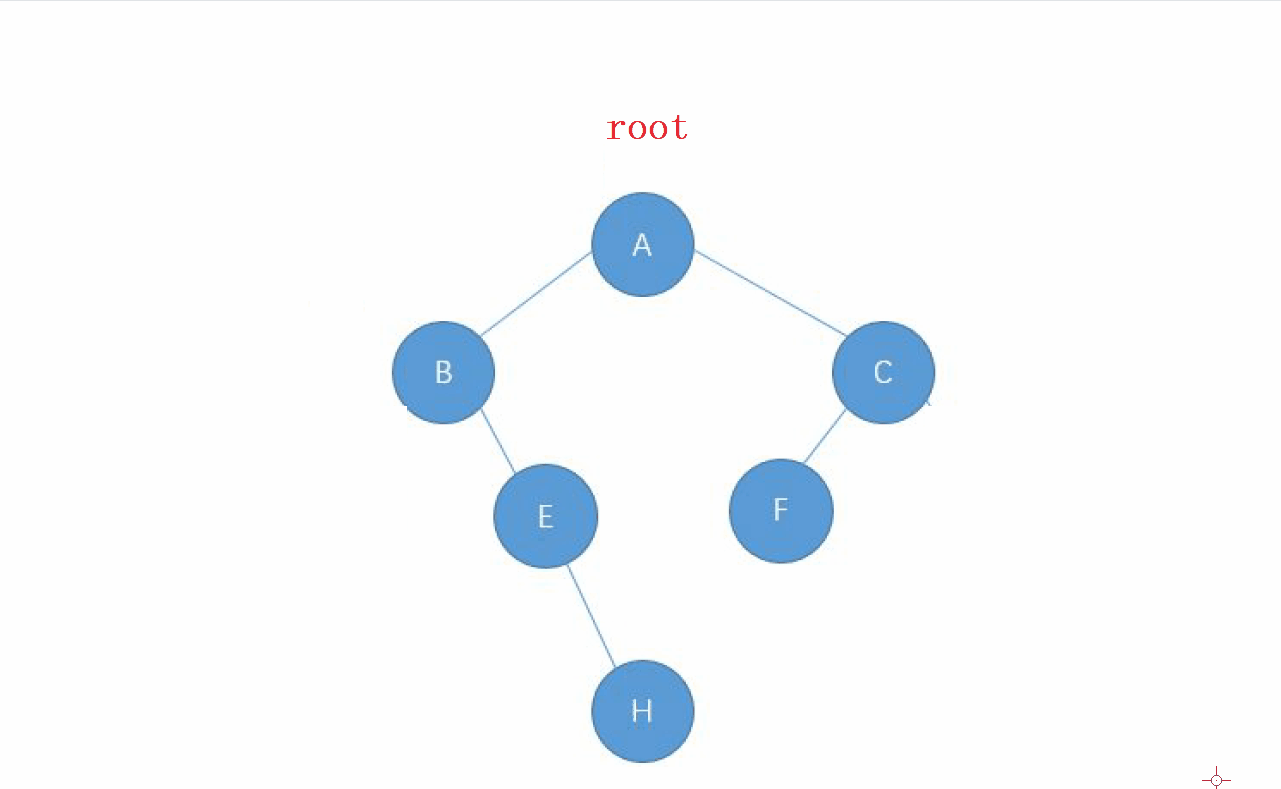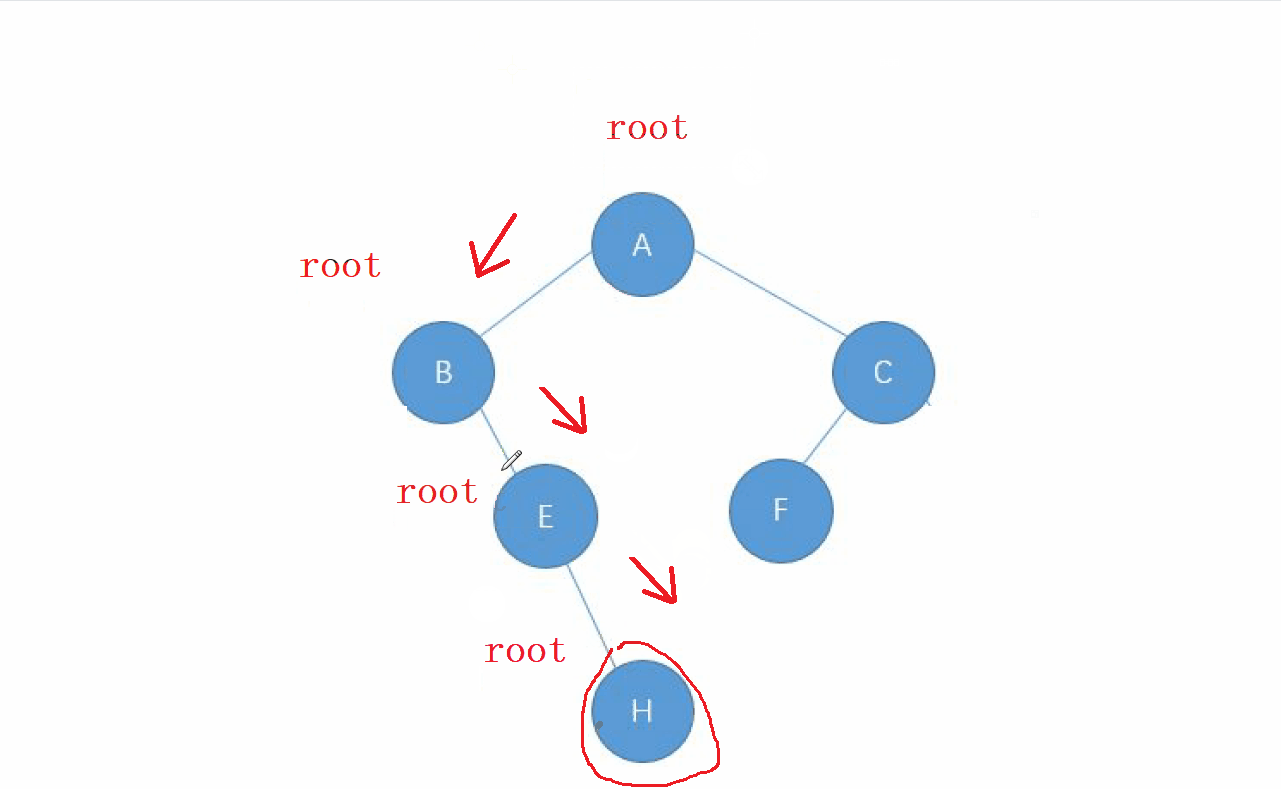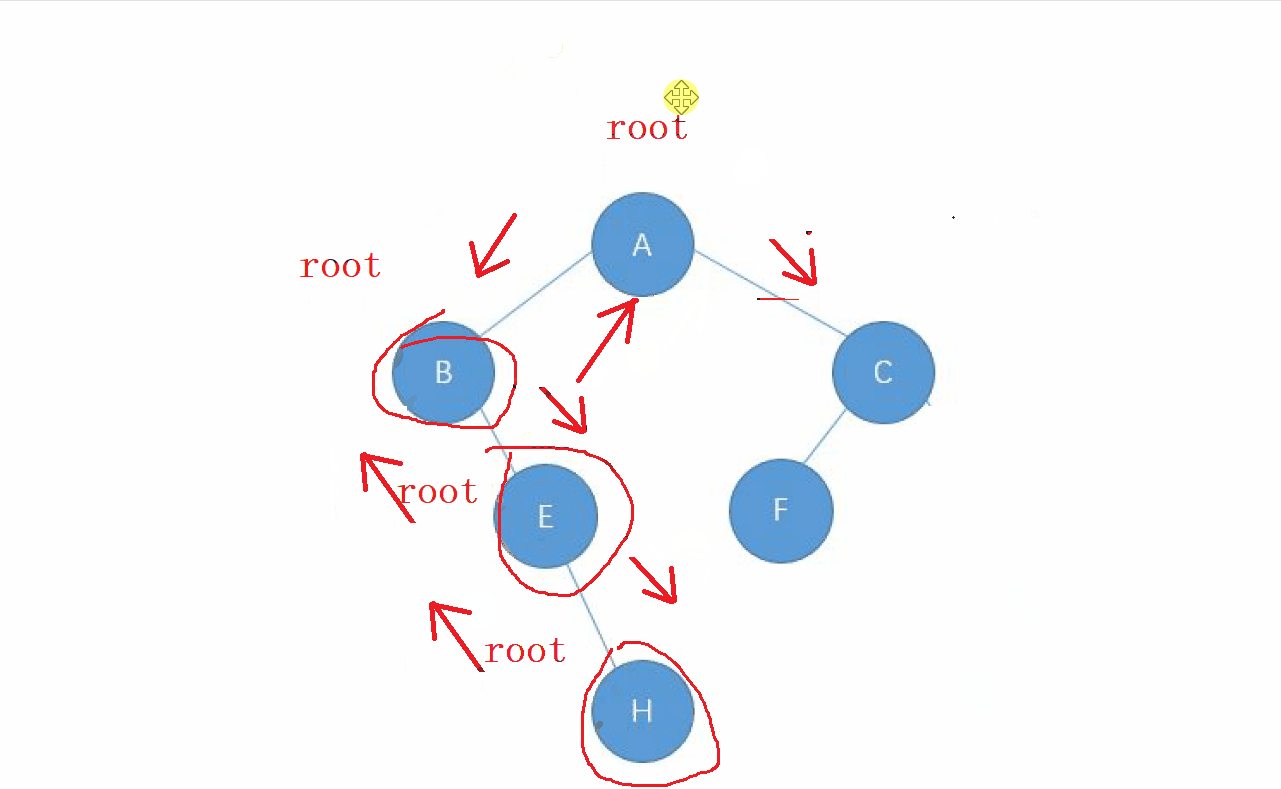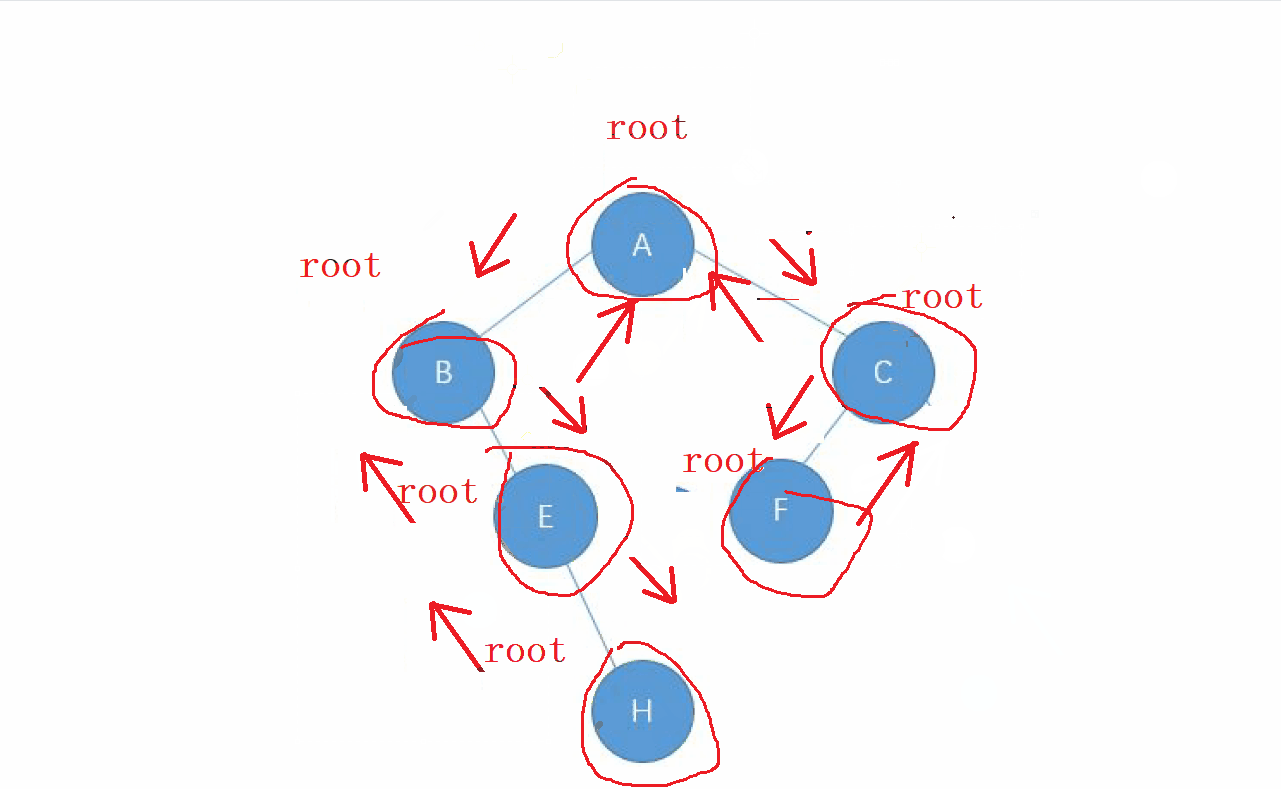
1. 后序遍历的特点
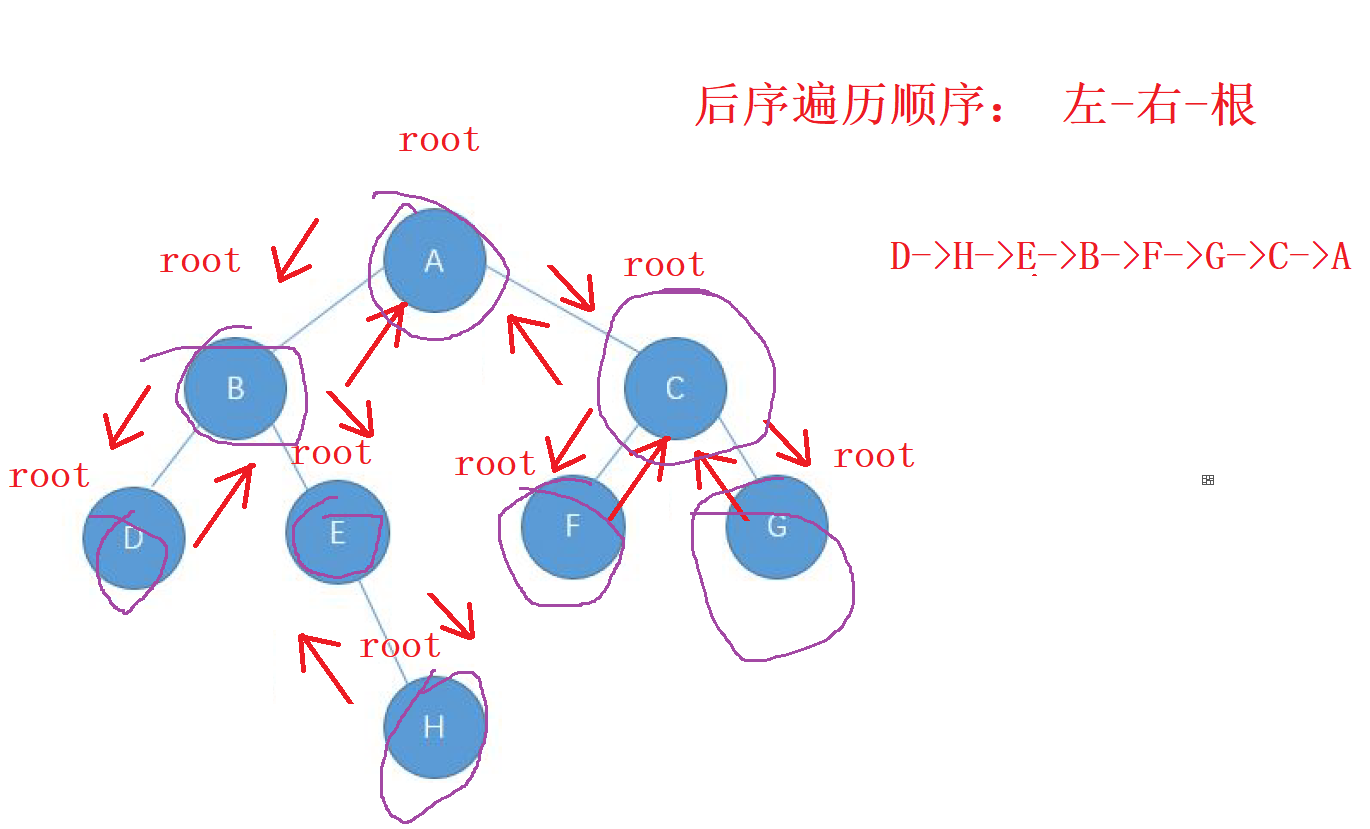
后序遍历的顺序就是 : 左-右-根 的顺序,
还是先走左边的节点,让 左边的节点 成为 新的根 , 直到找到走完整个
左子树,回退后继续走 右子树,当 右子树走完之后,回去的根节点就是我们要访问的
动画演示
2. 后序遍历的实现

<1>. 后序遍历的递归实现
// 后序遍历public void lastDisplay(TreeNode root) {if (root==null) {return;}lastDisplay(root.left);lastDisplay(root.right);System.out.print(root.val+" ");}
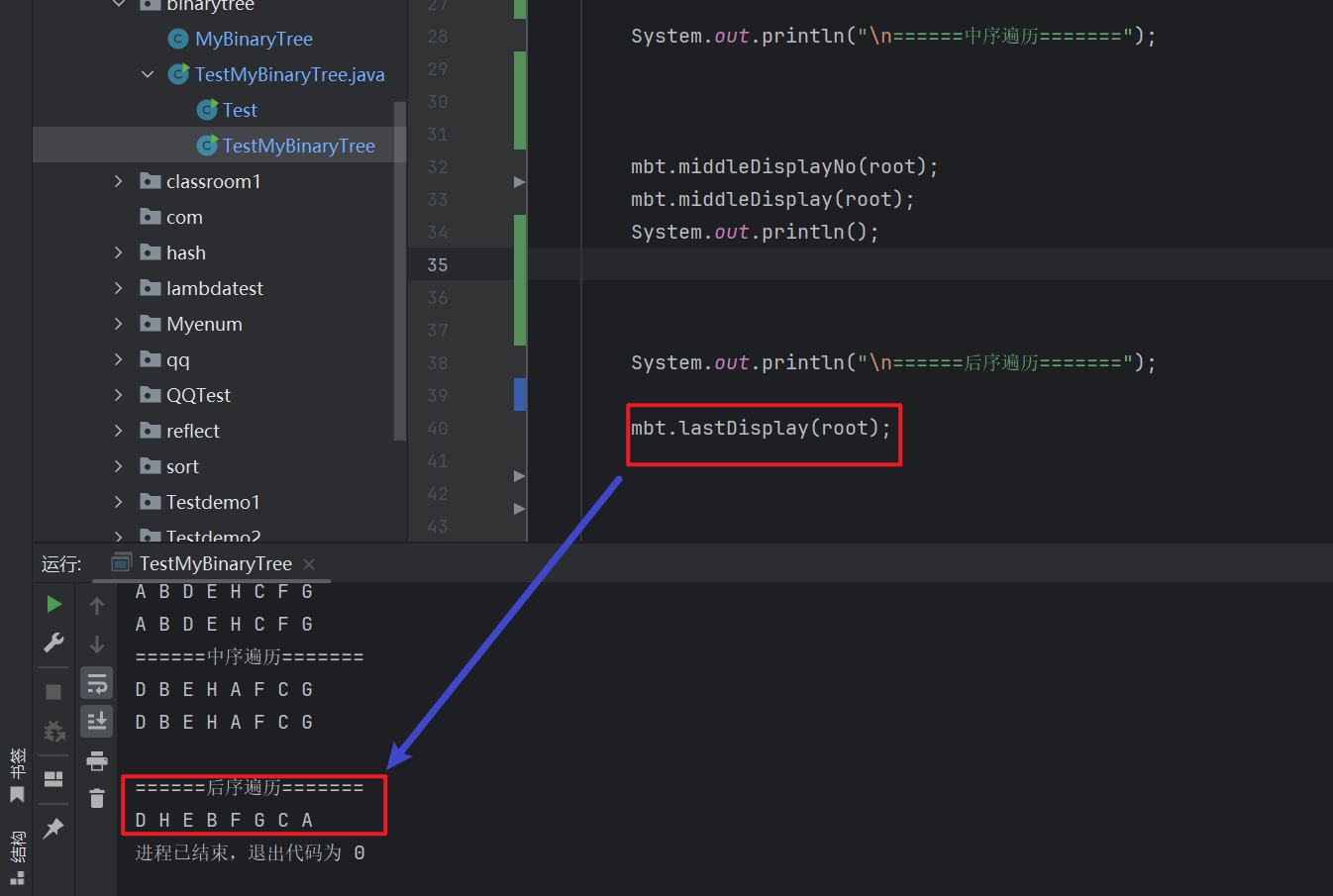
这里的代码的递归思路就是完美的按照我们遍历方向来的,
先递归,后访问,小编在这里就 不赘述 了
<2>. 后序遍历的非递归实现
// 非递归的后序遍历public void lastDisplayNo (TreeNode root) {Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;TreeNode flg=null;while (cur != null || !stack.empty()) {while (cur != null) {stack.add(cur);cur=cur.left;}TreeNode top=stack.peek();if (top.right == null || flg==top.right) {System.out.print(top.val+" ");flg=top;stack.pop();} else {cur=top.right;}}System.out.println();}
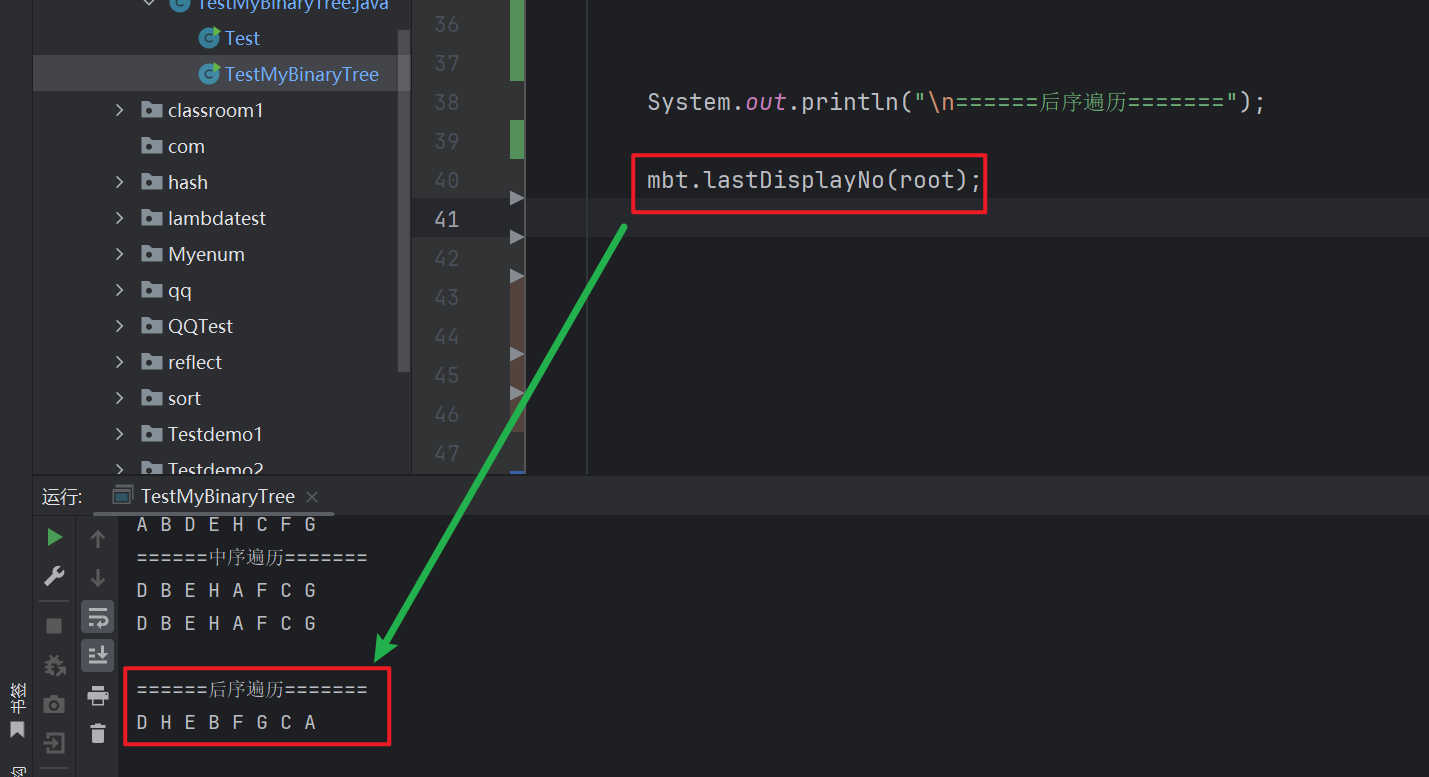
非递归的实现思路:
我们先定义一个栈,用来存放节点, 而这里存放的节点有可能是 左子树的节点,也有可能是 右子树的节点
- 先向左走,让左子树的节点先入栈
- 然后 查看栈顶元素,如果栈顶元素的
右节点为 null , 我们就打印(访问)该节点,
- 如果栈顶元素的
右节点不为 null , 我们就 让 该节点 向右走 , 并且入栈
- 以此循环往复,当
栈为 null并且 节点 cur 也为 null , 说明我们已经遍历完这个 二叉树所有的节点
鱼式疯言
无论是 非递归还是递归实现 对二叉树的 后序遍历
-
小伙伴们只需要记住一点: 后序遍历 一定是
两边先走完,最后回到我们的根节点才访问的 -
小伙伴们一定要把每个节点都看出一颗独立的树。每个节点 都是一个
独立的根节点来理解我们的三大遍历
TreeNode flg =nullif (top.right == null || flg==top.right) {System.out.print(top.val+" ");flg=top;stack.pop();}
细节处理: 我们需要用一个 flg 来记录上一个已经 访问过 的节点,判断 是否访问过, 防止再次让 top 向右走,继续入栈, 否则会进入 死循环
四. 层序遍历
谈及完前面的 三大遍历, 这些是我们 操作二叉树的根本 ,但还有还要介绍一种 比较特殊的遍历
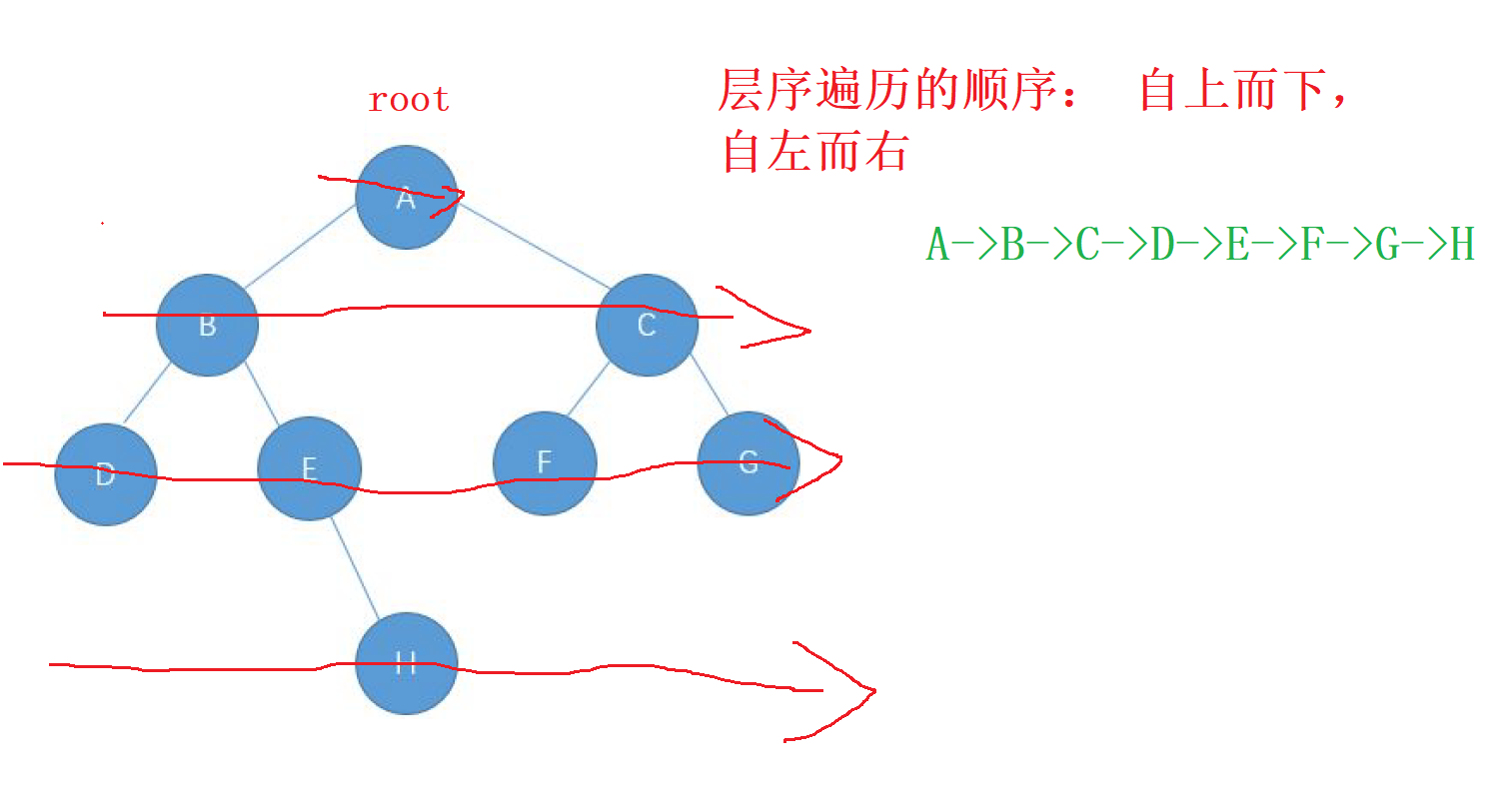
1. 层序遍历的特点
二叉树
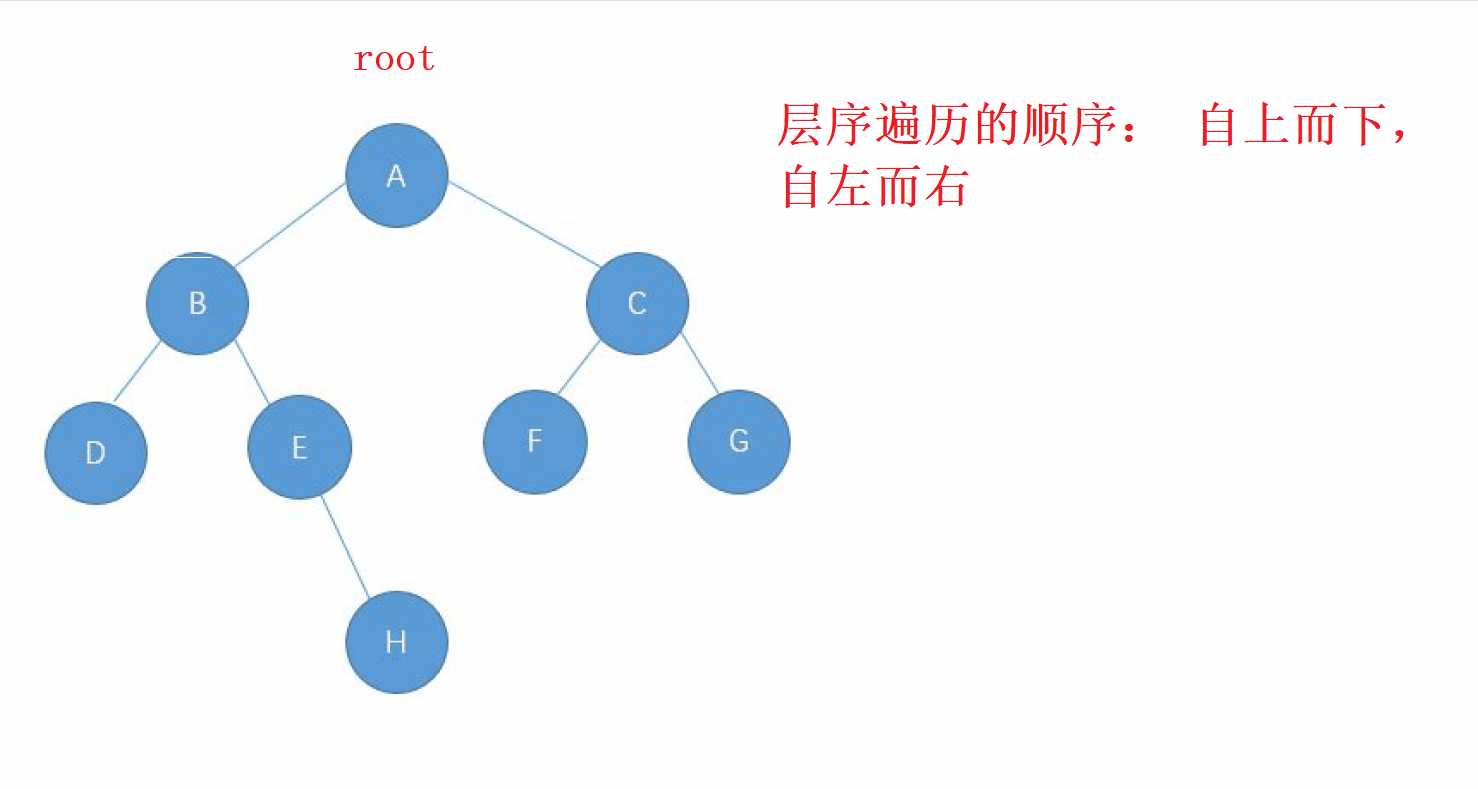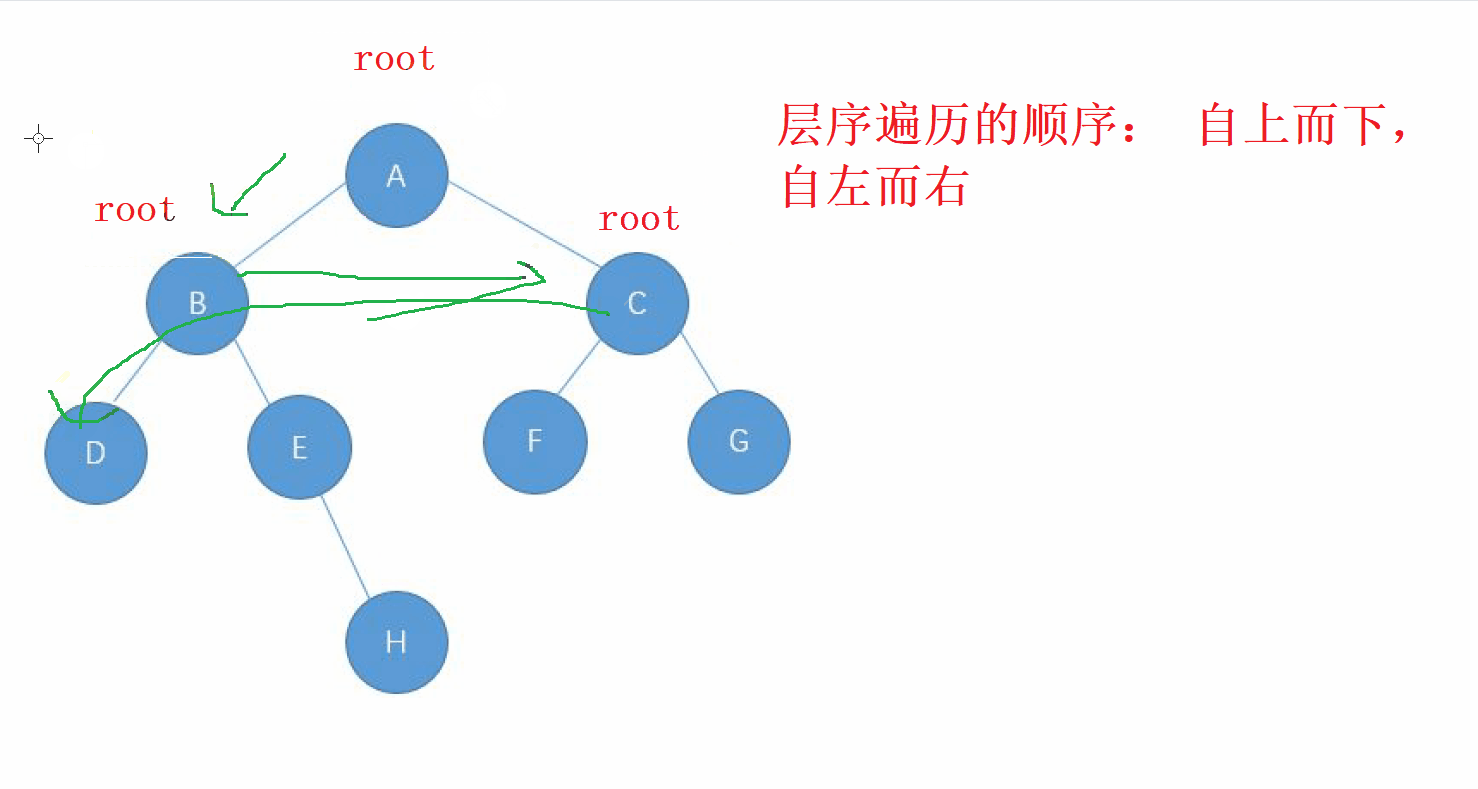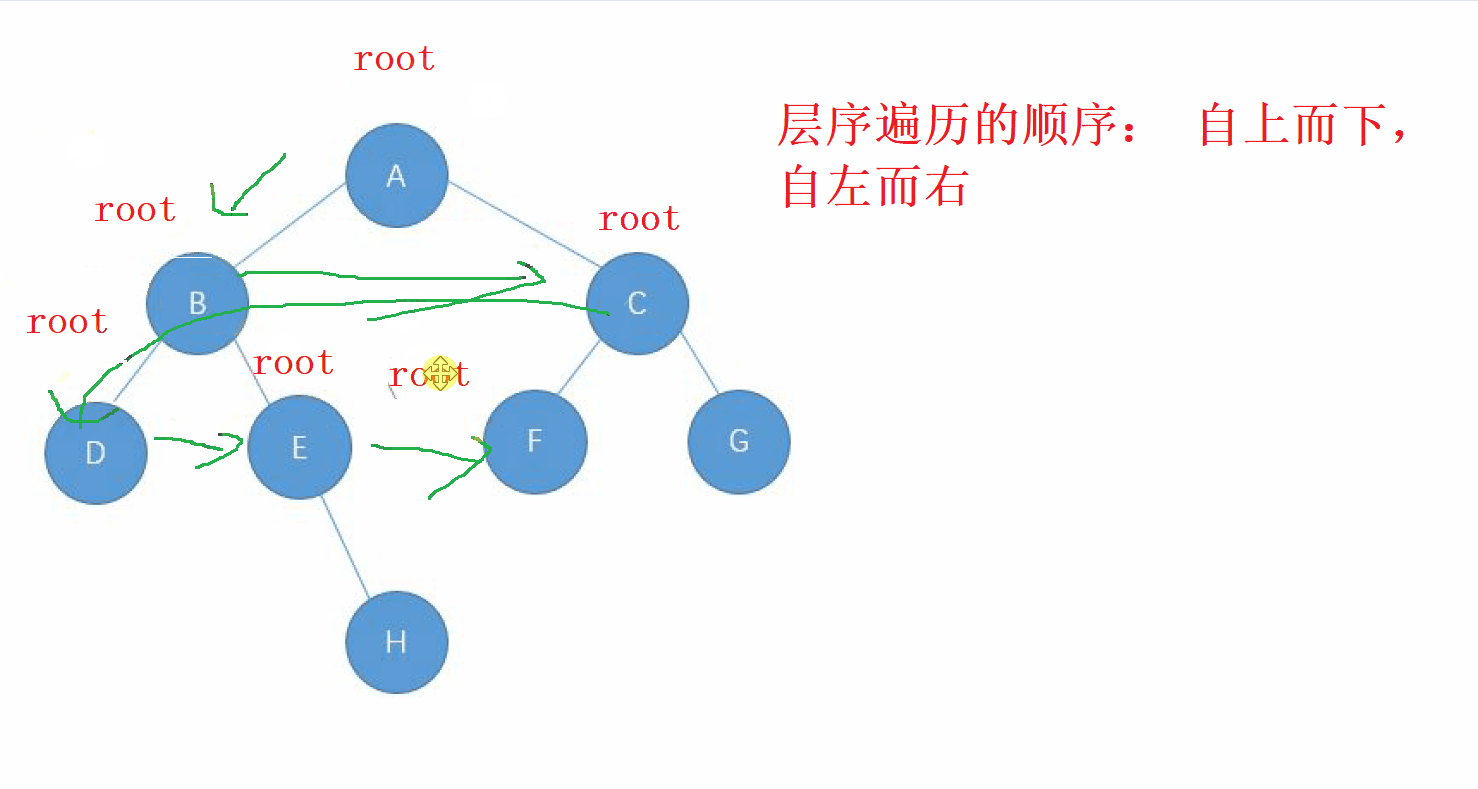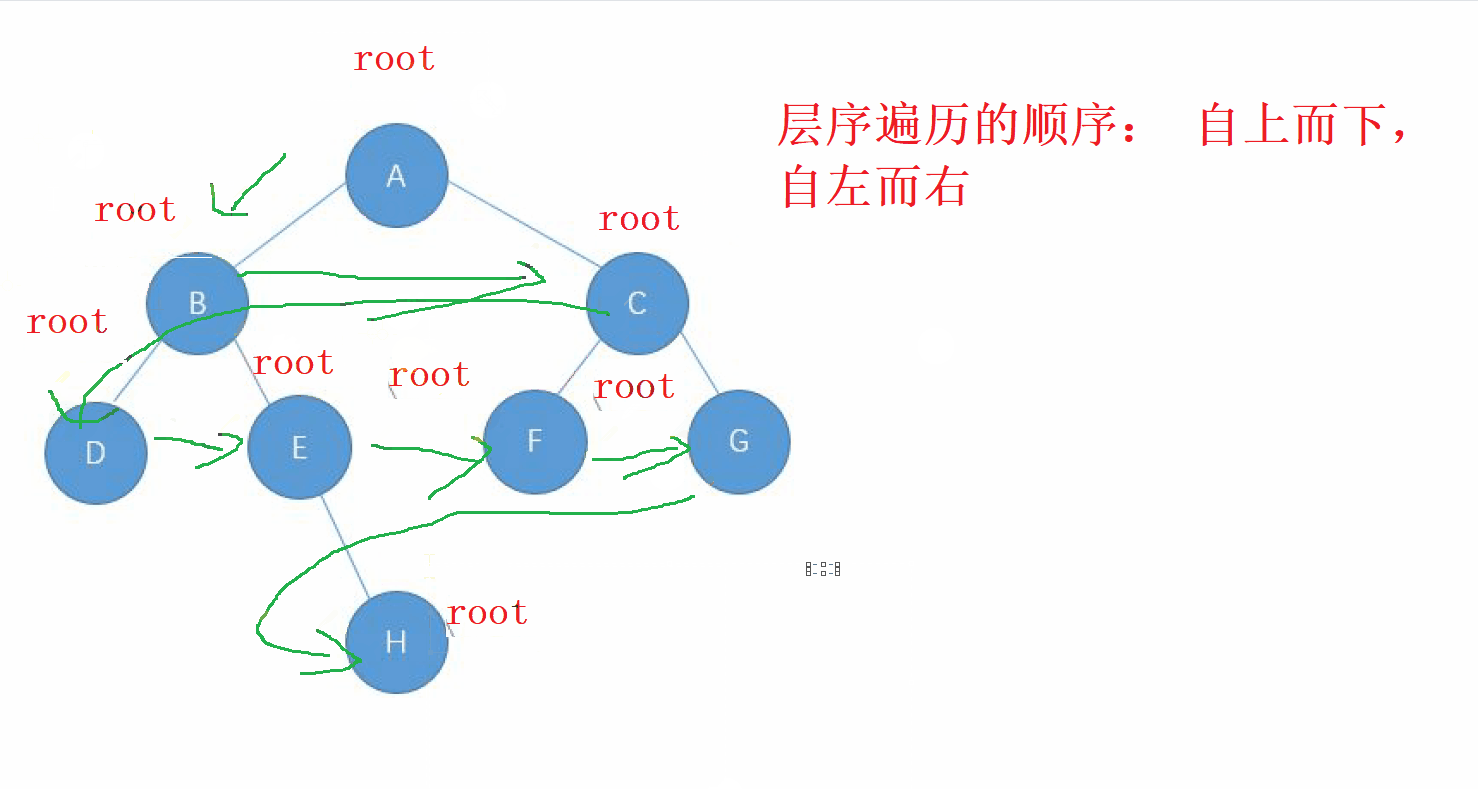
层序遍历的方向是从 根节点,按照 从上而下,从左到右 的顺序进行遍历 二叉树的每一个节点
动画演示
2. 层序遍历的实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/class Solution {List<List<Integer>> S=new ArrayList<List<Integer>>();public List<List<Integer>> levelOrder(TreeNode root) {if(root==null) {return S;}creatOrder(root,0);return S;}public void creatOrder(TreeNode root,int i) {if(root==null) {return ;}if(S.size()==i) {S.add(new ArrayList<Integer>());}S.get(i).add(root.val);creatOrder(root.left,i+1);creatOrder(root.right,i+1);}
}
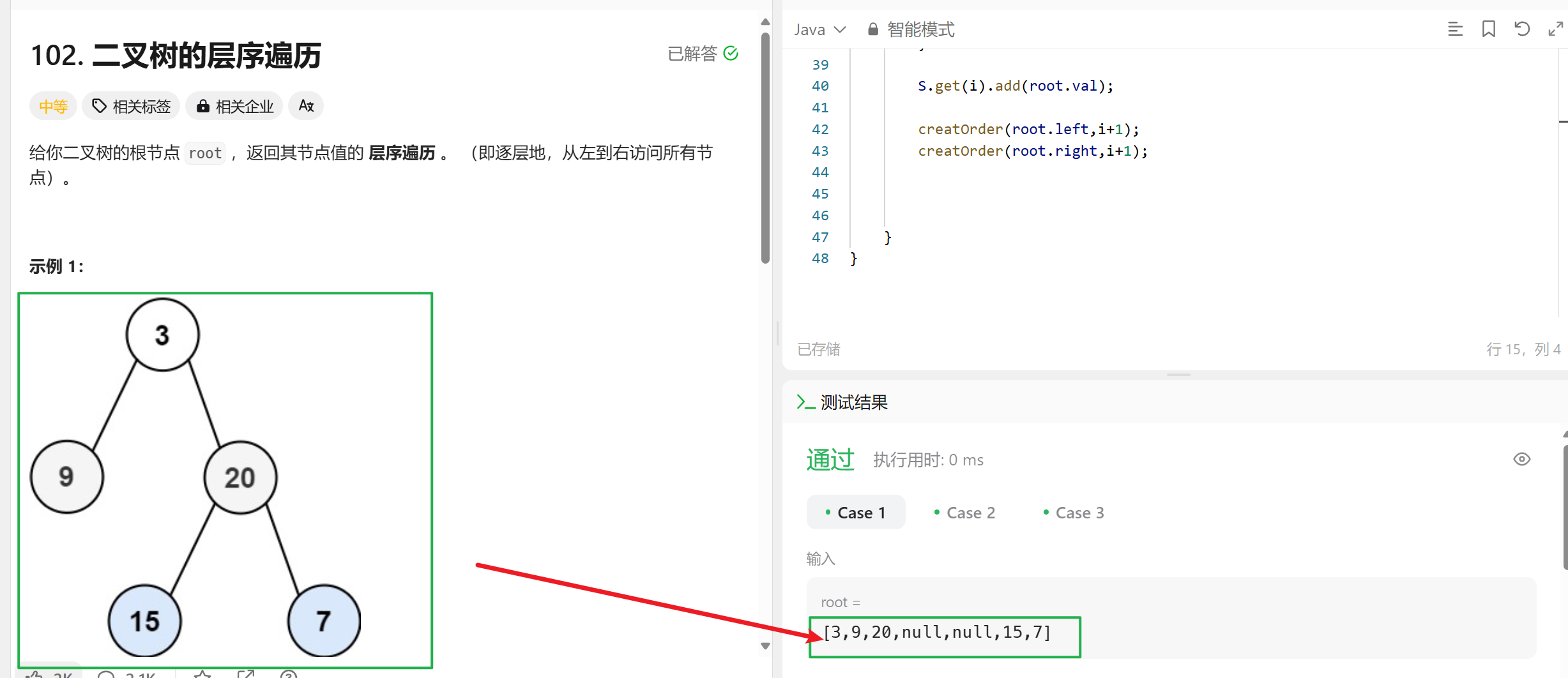
具体实现步骤:
-
我们用一个
二维数组(二维顺序表)来存储每一个节点,二叉树 每一层代表是二维数组的每一行, 在这二叉树每一层的行中,从左往右的节点 代表二维数组的每一列 -
当二叉树从
左子树开始递归, 意味着先存储 每一行 的二叉树的节点 -
当二叉树向
右子树开始递归, 意味着存储 每一列 的二叉树的节点 -
最终当整个二叉树完全递归就意味着 全部的节点都存储在 这个二维数组 (二维顺序表) 中
鱼式疯言
if(S.size()==i) {S.add(new ArrayList<Integer>());}
细节处理
每新添加
一行数据,需要扩容,就是需要再 实例化一个顺序表 ,已有的行数就不需要了
小伙伴们有没有发现,二叉树的层序遍历,本质上和我们的 完全二叉树的定义 是一样的,都是满足
自上而下,自左而右的特点
六. 二叉树遍历的应用
学习完了 二叉树遍历,小伙伴们是时候 牛刀小试 一下了 💞 💞 💞
1. 习题一:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG
B: ABCDEFGH
C: HDBEAFCG
D: HDEBFGCA
题目解析
我们知道了二叉树的 层序遍历 , 并且小伙伴们还有没有注意一个条件就是 完全二叉树
完全二叉树的特点就是
自上而下,自左而右节点不间断
那么我们不妨画个草图吧

画出草图,我们就很明显的知道了,答案选: A
2. 习题二:
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E
B: F
C: G
D: H
题目解析:
此题题目就是 答案, 我们知道前序遍历, 是从 根节点 开始的 , 所以 第一个访问出来的节点 就是我们的 根节点
故:答案选:A
3. 习题三:
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce
B: decab
C: debac
D: abcde
题目解析:
此题的精髓就在于,我们要根据 中序遍历 和 后序遍历 ,画出草图, 根据草图得到我们的 前序遍历

画草图的方法:
方法: 先根据后序遍历寻找 根节点
对于 后序遍历 来说:根节点是从右往左 , 然后结合 中序遍历的特点 来确定 左右节点 的位置
故此题答案选: D
4. 习题四:
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA
B: CBAFED
C: DEFCBA
D: ABCDEF
题目解析 :
此题的精髓就在于,我们要根据 中序遍历 和 后序遍历 ,画出草图, 根据草图得到我们的 层序遍历

依照上一题的方法,我们成功画出草图,最终得到我们的层序遍历
故答案选: A
鱼式疯言
独家秘方:
- 对于我们已知
前序和中序遍历,我们的方法就是根据 前序遍历从左往右 找根节点,然后结合 中序遍历画出草图
- 对于 我们已知的
后序和中序遍历, 我们的方法是 根据 后序遍历 从右往左找根节点 , 然后结合中序遍历画出草图
对于上述题目来说, 画图是 根本
总结
-
. 二叉树的遍历初识: 我们通过基本的概念知道了二叉树是通过一定
规则和方向来遍历我们 每一个节点 -
. 前序遍历 : 本源是 根-左-右的方向遍历
-
. 中序遍历: 本源是 左-根-右的方向遍历
-
.后序遍历 : 本质上还是根据 左-右-根的方向遍历
-
. 层序遍历: 遵循一个 自上而下, 自左而右 的顺序遍历
-
. 二叉树遍历的应用 : 我们主打一个对于这四种遍历的性质的理解和应用,来画图解题
如果觉得小编写的还不错的咱可支持 三连 下 (定有回访哦) , 不妥当的咱请评论区 指正
希望我的文章能给各位宝子们带来哪怕一点点的收获就是 小编创作 的最大 动力 💖 💖 💖

相关文章:

颠仆流离学二叉树2 (Java篇)
本篇会加入个人的所谓鱼式疯言 ❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言 而是理解过并总结出来通俗易懂的大白话, 小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的. 🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人…...

柏林自由大学研究团队《Ecology Letters 》揭示AMF在植物对全球变化响应的作用
全球环境变化正在影响陆生植物生长。植物已经进化出各种策略来应对这些挑战,其中之一是与丛枝菌根真菌(AMF)形成共生关系(高达80%的陆生植物物种)。AMF为寄主植物提供各种益处,例如营养吸收、耐受性、食草动物防御和抗病能力,以换取糖和脂质(…...

libevent源码跨平台编译(windows/macos/linux)
1.windows编译: 克隆: git clone https://github.com/libevent/libevent.git 克隆成功 生成makefile 生成成功 默认不支持OpenSSL,MbedTLS,ZLIB这三个库 编译: cmake --build . --config release...
idea+tomcat+mysql 从零开始部署Javaweb项目(保姆级别)
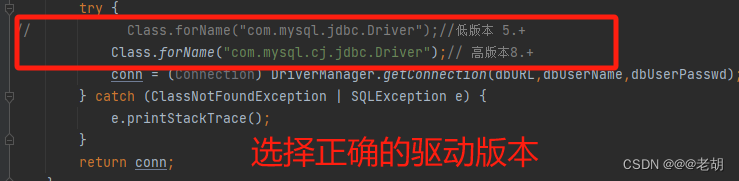
文章目录 新建一个项目添加web支持配置tomcat优化tomcat的部署运行tomcatidea数据库连接java连接数据库 新建一个项目 new project;Java;选择jdk的版本;next;next;填写项目名字,选择保存的路径;…...

LeetCode 每日一题 2024/5/27-2024/6/2
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 5/27 2028. 找出缺失的观测数据5/28 2951. 找出峰值5/29 2981. 找出出现至少三次的最长特殊子字符串 I5/30 2982. 找出出现至少三次的最长特殊子字符串 II5/31 2965. 找出缺…...

BOOST_SREATCH
BOOST Boost是一个由C社区开发的开源库,为C语言标准库提供扩展。这个库由C标准委员会库工作组成员发起,旨在提供大量功能和工具,帮助C开发者更高效地编写代码。Boost库强调跨平台性和对标准C的遵循,因此与编写平台无关࿰…...

MySQL学习——获取数据库和表格的信息
如果忘记了数据库或表的名称,或者不确定给定表的结构(例如,其列的名称),该怎么办呢?MySQL通过几个语句解决了这个问题,这些语句提供了有关它支持的数据库和表的信息。 你之前已经看过SHOW DATA…...

Go语言redis框架 — go-redis
https://zhuanlan.zhihu.com/p/645669818 一、简述 1. API友好,命令名称和参数与Redis原生命令一致,使用简单方便。 2. 支持完整的Redis命令集,覆盖了字符串、哈希、列表、集合、有序集合、HyperLogLog等数据结构。 3. 支持连接池&#x…...

C++ | Leetcode C++题解之第125题验证回文串
题目: 题解: class Solution { public:bool isPalindrome(string s) {int n s.size();int left 0, right n - 1;while (left < right) {while (left < right && !isalnum(s[left])) {left;}while (left < right && !isalnu…...
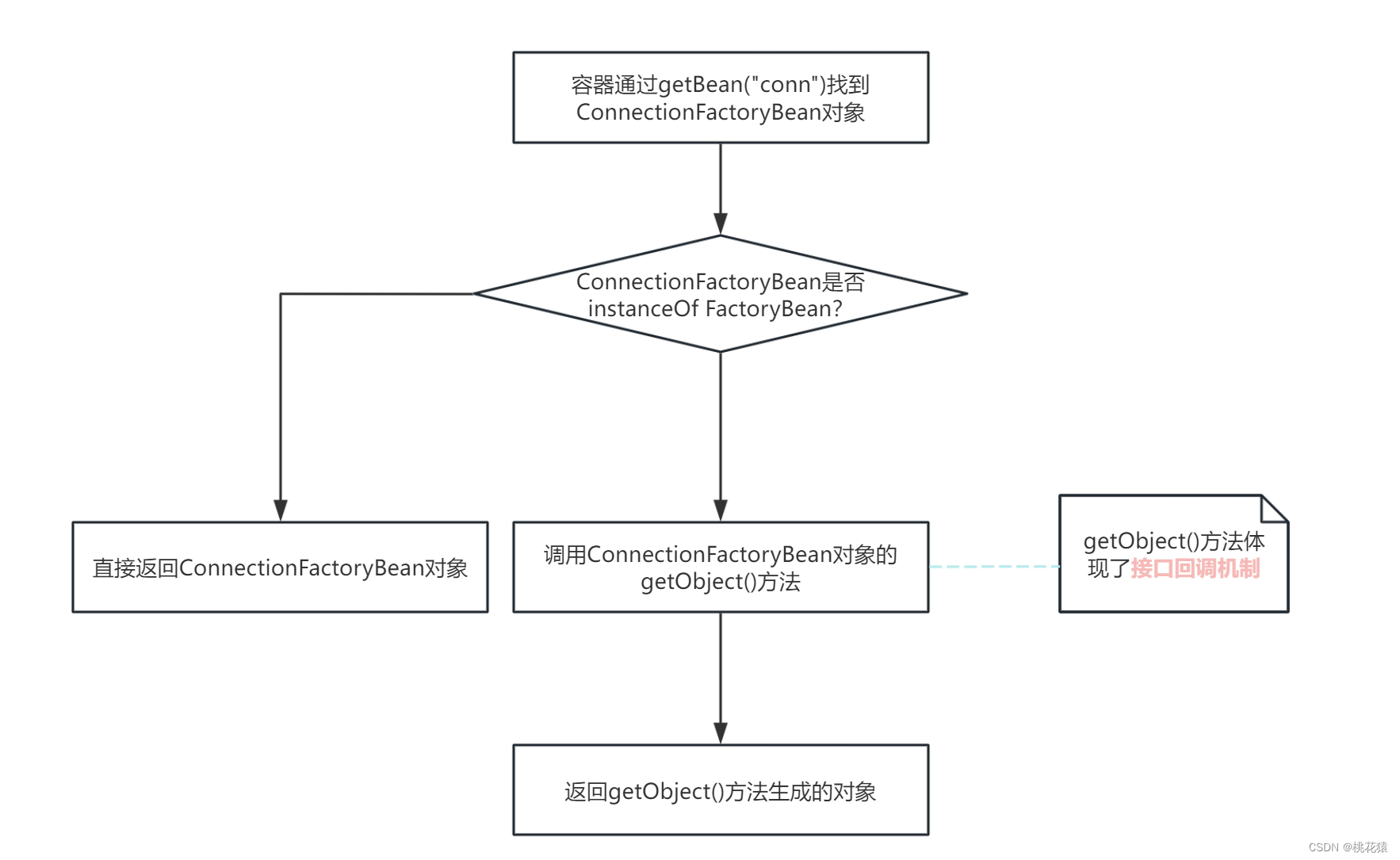
Spring创建对象的多种方式
一、对象分类 简单对象:使用new Obj()方式创建的对象 复杂对象:无法使用new Obj()方式创建的对象。例如: 1. AOP创建代理对象。ProxyFactoryBean; 2. Mybatis中的SqlSessionFactoryBean; 3. Hibernate中的SessionFactoryBean。二、创建对象方…...
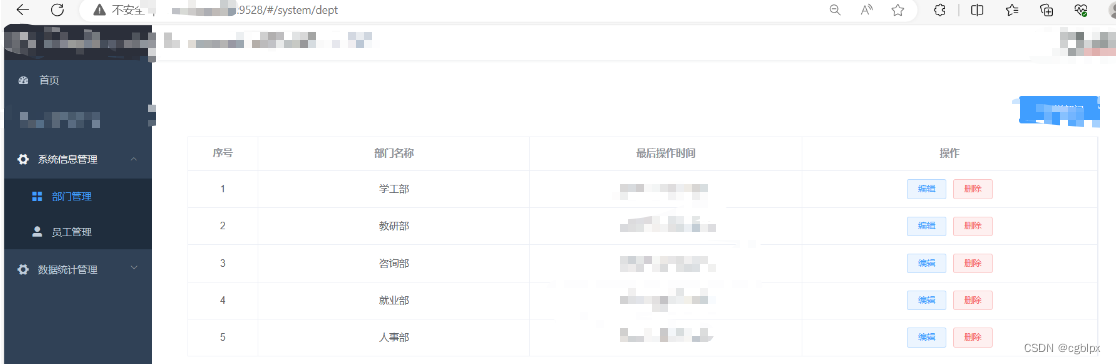
宝塔部署前后端分离项目手册
文章目录 安装宝塔安装环境开始部署1. 前端Vue项目1.先本地启动前端项目(记住端口号)2.打包前端项目3.上传前端项目4.创建PHP站点5.安全里开放端口号6.测试前端 2. 后端boot项目1. 先在本地跑起来2.修改数据库的配置信息3. 项目打包4. nohup启动项目4.1 …...

Leetcode 第 397 场周赛题解
Leetcode 第 397 场周赛题解 Leetcode 第 397 场周赛题解题目1:3146. 两个字符串的排列差思路代码复杂度分析 题目2:思路代码复杂度分析 题目3:3148. 矩阵中的最大得分思路代码复杂度分析 题目4:3149. 找出分数最低的排列思路代码…...

Python+Selenium自动化测试项目实战
第 1 章 自动化测试 1.1、自动化测试介绍 自动化测试就是通过自动化测试工具帮我们打开浏览器,输入网址,输入账号密码登录,及登录后的操作,总的说来自动化测试就是通过自动化测试脚本来帮我们从繁琐重复的手工测试里面解脱出来&…...
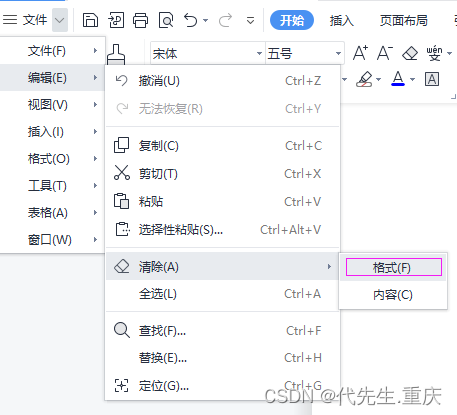
WPS部分快捷操作汇总
记录一些个人常用的WPS快捷操作 一、去除文档中所有的超链接: 1、用WPS打开文档; 2、用Ctrla全选,或者点击上方的【选择】-【全选】,选中文档全部内容; 3、按CTRLSHIFTF9组合键,即可一次性将取文档中所有…...
 普及指南)
Kubernetes (K8s) 普及指南
在当今的云计算和微服务时代,Kubernetes(简称K8s)已经成为容器编排的标准工具。它帮助开发者和运维人员管理和部署应用程序,实现高可用性、可伸缩性和自我修复。本文将详细介绍Kubernetes的基本概念、核心组件、工作原理及其优势。…...

Oracle RAC 集群配置共享目录ACFS
Oracle RAC 集群配置共享目录ACFS 应用场景:创建的ACFS文件系统用于部署OGG做数据同步使用。 1、创建共享磁盘组 create diskgroup OGG external redundancy disk /dev/mapper/ASM08, /dev/mapper/ASM09; 2、创建 acfs 文件系统 ACFS文件系统 在ASM磁盘组中通过A…...

Google Cloudbuild yaml file 中 entrypoint 和 args 的写法
编写cloudbuild.yaml 时有几个关键参数 entrypoint 和 args 的基本介绍 id: 显示在 cloud build logs 里的item 名字 name: docker 镜像名字 - 下面的命令会在这个镜像的1个容器instance 内执行 entrypoint: 执行的命令入口 , 只能有1个对象 args: 命名…...

鸿蒙开发接口图形图像:【@ohos.window (窗口)】
窗口 窗口提供管理窗口的一些基础能力,包括对当前窗口的创建、销毁、各属性设置,以及对各窗口间的管理调度。 该模块提供以下窗口相关的常用功能: [Window]:当前窗口实例,窗口管理器管理的基本单元。[WindowStage]&…...

LLM 基准测试的深入指南
随着越来越多的 LLM 可用,对于组织和用户来说,快速浏览不断增长的环境并确定哪些模型最适合他们的需求至关重要。实现这一目标的最可靠方法之一是了解基准分数。 考虑到这一点,本指南深入探讨了 LLM 基准的概念、最常见的基准是什么以及它们需要什么,以及仅依赖基准作为模…...

深入理解Redis事务、事务异常、乐观锁、管道
Redis事务与MySQL事务 不一样。原子性:MySQL有Undo Log机制,支持强原子性,和回滚。Redis只能保证事务内指令可以不被干扰的在同一批次执行,且没有机制保证全部成功则提交,部分失败则回滚。隔离性:MySQL的隔…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
