【U-Net验证】逐元素乘积将特征投射到极高维隐式特征空间的能力
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需使用请注明出处,同时如有侵犯您的权益,请联系删除!
文章目录
- 前言
- 网络结构
- 编码结构
- 解码结构
- 代码
- 实验
- 实验设置
- w/o-ReLU的性能比较
- with-ReLU的性能比较
- 总结
- 致谢
- 参考
前言
在深度学习领域,网络架构的创新和性能的提升一直是研究的热点。在传统的神经网络设计中,激活函数扮演着至关重要的角色,它们为网络引入了非线性,使得网络能够学习和表示复杂的模式和结构。
近年来,逐元素乘积作为一种简单的操作,在各类神经网络中展现出惊人的潜力。它不仅能够有效融合不同来源的信息。在博客【CVPR_2024】:逐元素乘积为什么会产生如此令人满意的结果? 揭示了逐元素乘积具有将特征投射到极高维隐式特征空间的能力,为设计紧凑和高效网络提供了思路。简言之,网络缺少激活函数,也可基于逐元素乘积为网络提供非线性。
为了验证逐元素乘积在神经网络中的性能,本文以眼底视网膜血管分割任务为例进行了实验。视网膜血管分割是医学图像处理中的一个重要任务,它对于眼科疾病的诊断和治疗具有重要意义。本文选择U-Net作为基础网络架构,并在其中引入逐元素乘积操作,以验证其在缺少激活函数时的网络性能。
网络结构
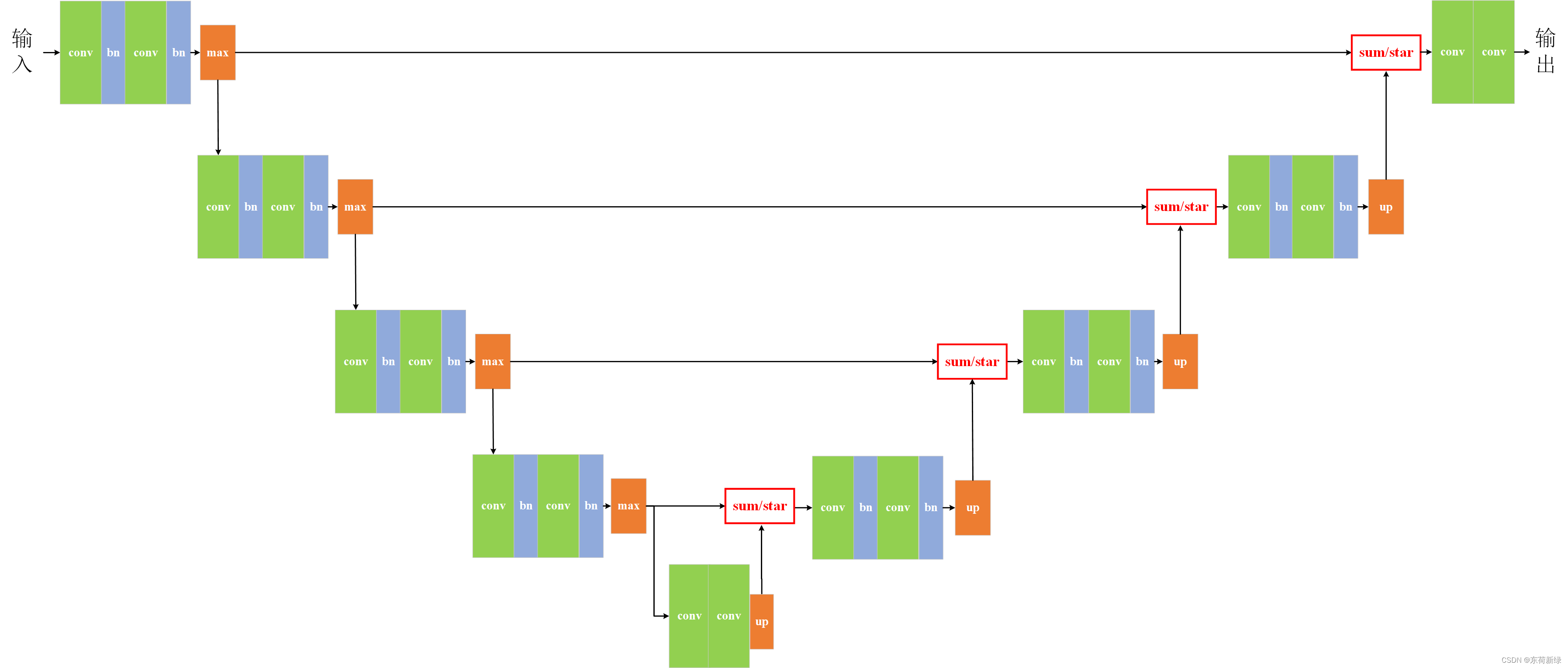
编码结构
U-Net的编码结构(Encoder)是一种专为图像分割任务设计的深度卷积神经网络的重要组成部分。U-Net的编码结构采用了一种典型的卷积神经网络(CNN)架构,其主要目的是从输入图像中提取有用的特征信息。该结构通常由多个重复的卷积块组成,每个卷积块包含卷积层、BN、激活函数和池化层。
区别于传统的unet,本文去除了编码阶段所有激活函数,即编码部分只包含卷积、BN和池化层,结构如下图。具体组成:
卷积层:卷积核大小为3x3,步长(stride)为1,填充(padding)为1。
池化层:池化窗口的大小通常为2x2,步长为2。

解码结构
U-Net的解码结构是U-Net网络中的关键部分,主要用于从编码器提取的特征中恢复图像的空间分辨率和细节。解码器通过上采样操作逐步恢复图像尺寸,并与编码器中的对应层通过跳跃连接进行特征融合,以恢复丢失的空间信息。
区别于传统的unet,本文去除了解码阶段所有激活函数,即解码部分只包含卷积、BN和上采样层,结构如下图。具体组成:
上采样层:最邻近插值法。
卷积层:卷积核大小为3x3,步长(stride)为1,填充(padding)为1。

代码
需要注意的是,本文为说明逐元素乘积的性能,将解码阶段中特征图拼接换为了sum/star,使得网络的参数进一步减少,网络更加紧凑。
同时,网络传入参数,设置了narrow,channel_multiplier参数用于控制网络通道以实现对网络参数的控制,return_feats参数则用于选择是否需要深度监督。
# ==============================U_Net—without ReLU====================================
class encode_block_wo_relu(nn.Module):def __init__(self, ch_in, ch_out):super(encode_block_wo_relu, self).__init__()self.conv = nn.Sequential(nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1, bias=True),NormLayer(ch_out, 'bn'),nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1, bias=True),NormLayer(ch_out, 'bn'),)self.down = nn.MaxPool2d(kernel_size=2, stride=2)def forward(self, x):skip = self.conv(x)x = self.down(skip)return x, skipclass decode_block_wo_relu(nn.Module):def __init__(self, ch_in, ch_out):super(decode_block_wo_relu, self).__init__()self.conv = nn.Sequential(nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1, bias=True),NormLayer(ch_out, 'bn'),nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1, bias=True),NormLayer(ch_out, 'bn'),UpsampleLayer())def forward(self, x):x = self.conv(x)return xclass U_Net_wo_relu(nn.Module):def __init__(self, img_ch=3, output_ch=1, narrow=0.5, channel_multiplier=1, return_feats=False):super(U_Net_wo_relu, self).__init__()channels = {'32': int(32 * channel_multiplier * narrow),'64': int(64 * channel_multiplier * narrow),'128': int(128 * channel_multiplier * narrow),'256': int(256 * channel_multiplier * narrow),'512': int(512 * channel_multiplier * narrow),'1024': int(1024 * channel_multiplier * narrow),'2048': int(2048 * channel_multiplier * narrow),'4096': int(4096 * channel_multiplier * narrow),}self.return_feats = return_featsself.up = UpsampleLayer()self.encoder = nn.ModuleList()self.decoder = nn.ModuleList()self.encoder.append(encode_block_wo_relu(img_ch, channels['64']))for i in range(0, 3):self.encoder.append(encode_block_wo_relu(channels[f'{64 * 2 ** i}'], channels[f'{64 * 2 ** (i + 1)}']))self.decoder.append(decode_block_wo_relu(channels[f'512'], channels[F'512']))for i in range(3, 0, -1):self.decoder.append(decode_block_wo_relu(channels[f'{int(64 * 2 ** i)}'], channels[f'{int(64 * 2 ** (i-1))}']))self.out = nn.Conv2d(channels['64'], output_ch, kernel_size=1)def forward(self, x):skips = []feats = []# encodefor enc in self.encoder:x, skip = enc(x)skips.append(skip)skips = skips[::-1]# decodefor i, dec in enumerate(self.decoder):x = dec(x)# print(x.shape, skips[i].shape)if i < len(self.decoder) - 1:# x = x + skips[i]x = x * skips[i]if self.return_feats:feats.append(x)out = self.out(x)pre = F.softmax(out, dim=1)return pre, feats
实验
实验设置
实验的设置如下:
| 随机种子 | 验证集比例 | 批大小 | 早停 | 学习率 | 优化器 | 图像大小 | 数据集 |
|---|---|---|---|---|---|---|---|
| 2024 | 0.2 | 8 | 10 | 0.0005 | adam | 96x96 | STARE |
所有方法均在相同的设置下进行实验,保证实验的公平性,网络参数为2.94M,均选择在验证集上表现最优的权重进行测试。
w/o-ReLU的性能比较
下图给了sum和star两种方法的性能对比:
 sum-w/o-ReLU-ROC曲线 sum-w/o-ReLU-ROC曲线 |  sum-w/o-ReLU-PR曲线 sum-w/o-ReLU-PR曲线 |
 star-w/o-ReLU-ROC曲线 star-w/o-ReLU-ROC曲线 |  star-w/o-ReLU-PR曲线 star-w/o-ReLU-PR曲线 |
| 操作类型 | ROC | PR | F1 | Acc | SE | SP | pre |
|---|---|---|---|---|---|---|---|
| sum-w/o-ReLU | 0.9039 | 0.7139 | 0.6530 | 0.9271 | 0.5939 | 0.9706 | 0.7251 |
| star-w/o-ReLU | 0.9312 | 0.7407 | 0.6835 | 0.9330 | 0.6271 | 0.9729 | 0.7511 |
| 提升 | ↑ 2.73 % \textcolor{red}{\uparrow 2.73\%} ↑2.73% | ↑ 2.68 % \textcolor{red}{\uparrow 2.68\%} ↑2.68% | ↑ 3.05 % \textcolor{red}{\uparrow 3.05\%} ↑3.05% | ↑ 0.59 % \textcolor{red}{\uparrow 0.59\%} ↑0.59% | ↑ 3.32 % \textcolor{red}{\uparrow 3.32\%} ↑3.32% | ↑ 0.23 % \textcolor{red}{\uparrow 0.23\%} ↑0.23% | ↑ 2.60 % \textcolor{red}{\uparrow 2.60\%} ↑2.60% |
 sum-w/o-ReLU sum-w/o-ReLU |
 star-w/o-ReLU star-w/o-ReLU |
如上所示,star操作在各个指标上均取得了更佳的性能,分别获得了0.2%到3%不等的提升,从定性的图像中来看,网络似乎对较大的血管具有更好的分割效果,同时血管分割的结果也更加光滑。
with-ReLU的性能比较
下图给了sum和star两种方法的性能对比:
 sum-with-ReLU-ROC曲线 sum-with-ReLU-ROC曲线 |  sum-with-ReLU-PR曲线 sum-with-ReLU-PR曲线 |
 star-with-ReLU-ROC曲线 star-with-ReLU-ROC曲线 |  star-with-ReLU-PR曲线 star-with-ReLU-PR曲线 |
| 操作类型 | ROC | PR | F1 | Acc | SE | SP | pre |
|---|---|---|---|---|---|---|---|
| sum-with-ReLU | 0.9743 | 0.8732 | 0.7846 | 0.9500 | 0.7888 | 0.9710 | 0.7805 |
| star-with-ReLU | 0.9706 | 0.8613 | 0.7750 | 0.9483 | 0.7715 | 0.9713 | 0.7786 |
| 提升 | ↓ 0.37 % \textcolor{blue}{\downarrow 0.37\%} ↓0.37% | ↓ 1.19 % \textcolor{blue}{\downarrow 1.19\%} ↓1.19% | ↓ 0.96 % \textcolor{blue}{\downarrow 0.96\%} ↓0.96% | ↓ 0.17 % \textcolor{blue}{\downarrow 0.17\%} ↓0.17% | ↓ 1.73 % \textcolor{blue}{\downarrow 1.73\%} ↓1.73% | ↑ 0.03 % \textcolor{red}{\uparrow 0.03\%} ↑0.03% | ↓ 0.19 % \textcolor{blue}{\downarrow 0.19\%} ↓0.19% |
 sum-with-ReLU sum-with-ReLU |
 star-with-ReLU star-with-ReLU |
如上所示,star操作在各个指标上均有不同程度的下降,总体来说,两者的性能差不多,从定性的图像中来看,star操作对血管连续上有较差的表现。
总结
本文将U-Net解码中的特征拼接修改为逐元素求和和逐元素乘积,并针对血管分割任务进行了性能评估。实验结果显示,在无激活函数时,逐元素乘积在多个关键指标上均优于逐元素求和,性能提升幅度在0.2%至3%之间,表明逐元素乘积确实能在一定程度上提供更高维度的隐式空间。从分割结果来看,逐元素乘积似乎对较大的血管具有更好的分割效果,能够更准确地捕捉血管的轮廓和细节。同时,star网络的分割结果也表现出更高的光滑性和一致性,减少了噪声和伪影的干扰,从而提高了分割结果的可靠性和可读性。在使用激活函数时,逐元素乘积在多个关键指标上均低于于逐元素求和,表明逐元素乘积的优势会倍激活函数所湮没。总言之,网络中要摒弃激活函数还有很长的路要走。
致谢
欲尽善本文,因所视短浅,怎奈所书皆是瞽言蒭议。行文至此,诚向予助与余者致以谢意。
参考
- 【CVPR_2024】:逐元素乘积为什么会产生如此令人满意的结果?
- GitHub-SkelCon
相关文章:

【U-Net验证】逐元素乘积将特征投射到极高维隐式特征空间的能力
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需使用请注明出处,同时如有侵犯您的权益,请联系删除! 文章目录 前言网络结构编码结构解码结构代码 实验实验设置w/o-ReLU的性能比较with-ReLU的性能比…...

快团团大团长帮卖如何导出单个团购的订单?免费教程教你怎么做!
一、小程序端如何导出单个团购的订单? 进入团购页面,在订单管理——订单导出中,点击订单数据表格,可导出到邮箱,或通过在浏览器中查看下载链接 二、电脑端如何导出单个团购的订单? 1、如何自定义选择订单信…...
services层和controller层
services层 我的理解,services层是编写逻辑代码语句最多的一个层,非常重要,在实际的项目中,负责调用Dao层中的mybatis,在我的项目中它调用的是这两个文件 举例代码如下 package com.example.sfdeliverysystem.servic…...

Pycharm编辑器下自定义模块导入报错:no module named问题
相信很多使用pycharm 社区版编写python 程序的初学者都会遇到这样一个看似简单但是一时半刻找不到解决头绪的问题: 在同个目录下导入自己编写的模块到主程序的过程中,直接import的时候会报错:ModuleNotFoundError。 通过各种方法尝试以后还是…...
C#使用GDI对一个矩形进行任意角度旋转
C#对一个矩形进行旋转GDI绘图,可以指定任意角度进行旋转 我们可以认为一张图片Image,本质就是一个矩形Rectangle,旋转矩形也就是旋转图片 在画图密封类 System.Drawing.Graphics中, 矩形旋转的两个关键方法 //设置旋转的中心点 public v…...

打印机的ip不同且连不上
打印机的ip不同且连不上 1.问题分析2.修改网段3.验证网络 1.问题分析 主要是打印机的网段和电脑不在同一个网段 2.修改网段 3.验证网络...
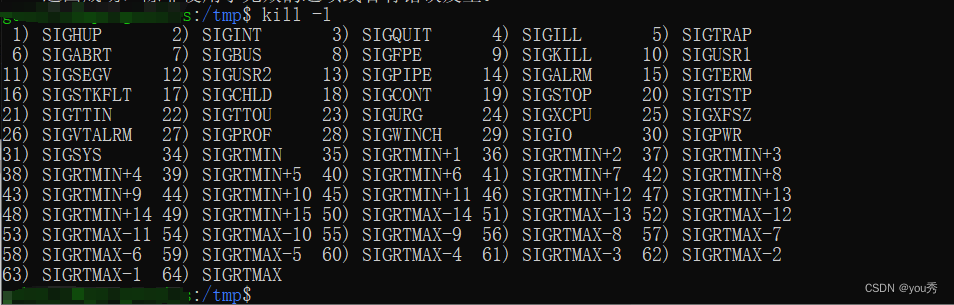
关于linux程序的查看、前台运行、后台运行、杀死的管理操作。
前言 在Linux中, 程序(program)是放在磁盘上的程序,是不会执行的。 进程(process)是程序被触发,从而加载到内存中的,会被CPU随机执行。 Linux中,有非常多的进程在实时运…...

STM32作业设计
目录 STM32作业设计 STM32作业实现(一)串口通信 STM32作业实现(二)串口控制led STM32作业实现(三)串口控制有源蜂鸣器 STM32作业实现(四)光敏传感器 STM32作业实现(五)温湿度传感器dht11 STM32作业实现(六)闪存保存数据 STM32作业实现(七)OLED显示数据 STM32作业实现(八)触摸按…...
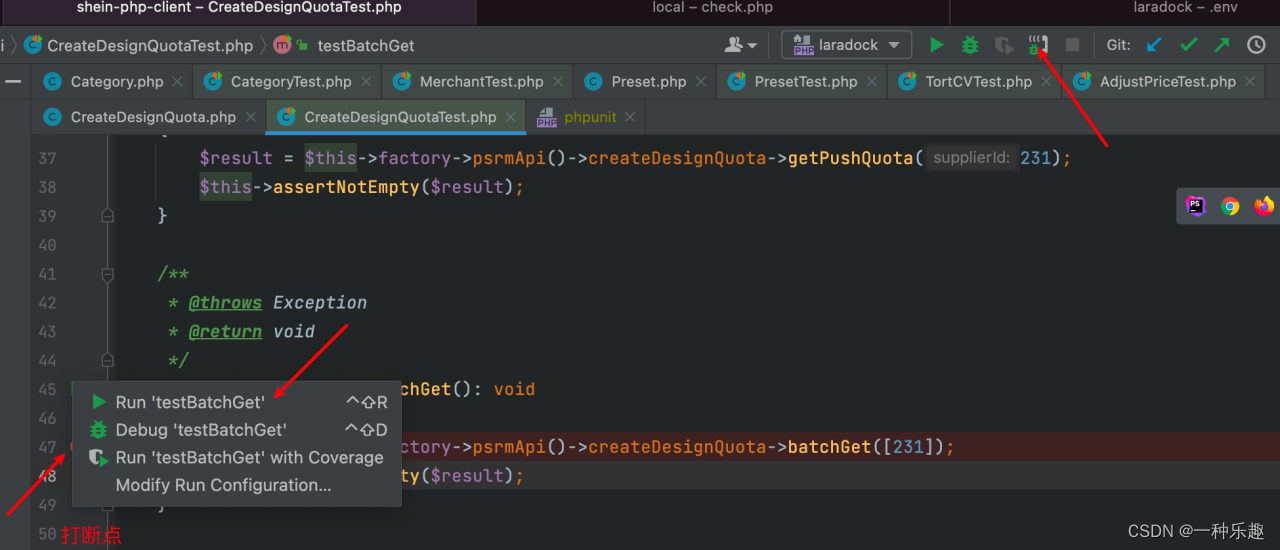
PHPSTOM配置Laradock,xdebug,phpunit
原理图: 片面理解: phpstorm启用一个9000端口,这个端口用来接收到信息后,启用xdebug功能。服务器端(docker), 当客户端访问laravel项目域名后, 并读取xdebug.ini的配置, 把调试的请求数据, 向配置里面的端口发送消息, 配置里面的端…...

使用Java进行数据分析和处理:应用在实际业务场景中的技术
在当今数据驱动的时代,数据分析和处理已经成为各行各业中不可或缺的一部分。Java作为一种广泛应用于企业级开发的编程语言,也在数据领域展现出了强大的能力。本文将探讨如何使用Java进行数据分析和处理,以及在实际业务场景中应用的技术。 ##…...

C++中的List
摘要 C 标准库中的 std::list 是一种双向链表容器,它允许在常数时间内进行插入和删除操作,每个元素包含一个指向前一个和后一个元素的指针。这给我们开发提供了高效的插入和删除操作。 引入头文件 要使用 std::list,需要包含头文件 <li…...

go map 如何比较两个 map 相等
go map 如何比较两个 map 相等 都为 nil非空、长度相等,指向同一个 map 实体对象相应的 key 指向的 value 相等 直接将使用 map1 map2 是错误的。这种写法只能比较 map 是否为 nil。因此只能是遍历map 的每个元素,比较元素是否都是深度相等。...

牛客网刷题 | BC108 反斜线形图案
目前主要分为三个专栏,后续还会添加: 专栏如下: C语言刷题解析 C语言系列文章 我的成长经历 感谢阅读! 初来乍到,如有错误请指出,感谢! 描述 KiKi学习了循环&am…...

数据的表示和运算
目录 一.各进制间的相互转换 1.各进制转化为10进制 2.二进制和八进制,十六进制之间地相互转化 3.十进制转换为其他进制 二.BCD码(Binary-Coded Decimal,用二进制编码的十进制) 1.8421码 2.余3码 3.2421码 三.无符号整数 …...
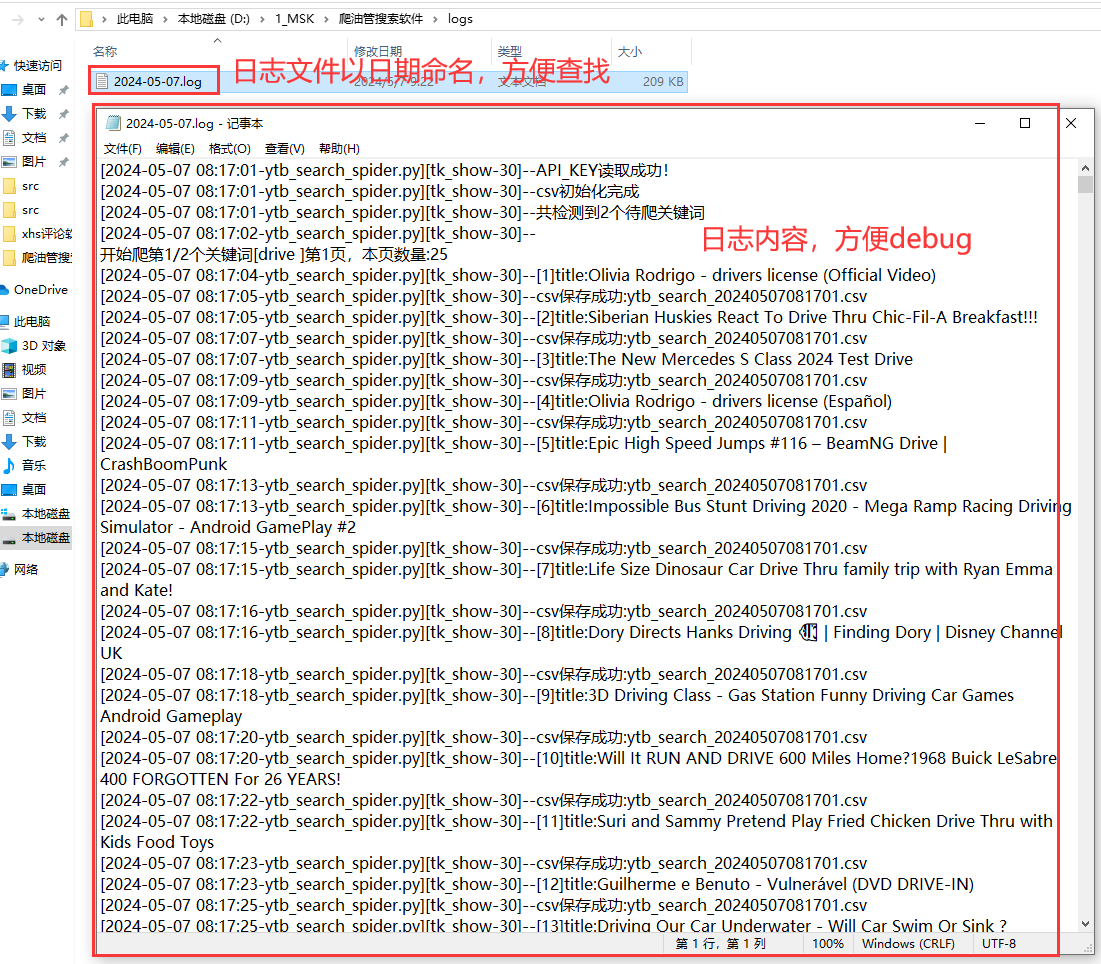
【爬虫工具】油管视频批量采集软件
一、背景介绍 1.1 爬取目标 我用Python独立开发了一款爬虫软件,作用是:通过搜索关键词采集ytb的搜索结果,包含14个关键字段:关键词,页码,视频标题,视频id,视频链接,发布时间,视频时长,频道名称,频道id,频道链接,播放数,点赞数,评…...

【LeetCode刷题】二分查找:寻找旋转排序数组中的最小值、点名
【LeetCode刷题】Day 14 题目1:153.寻找旋转排序数组中的最小值思路分析:思路1:二分查找:以A为参照思路2:二分查找,以D为参照 题目2:LCR 173.点名思路分析:思路1:遍历查找…...
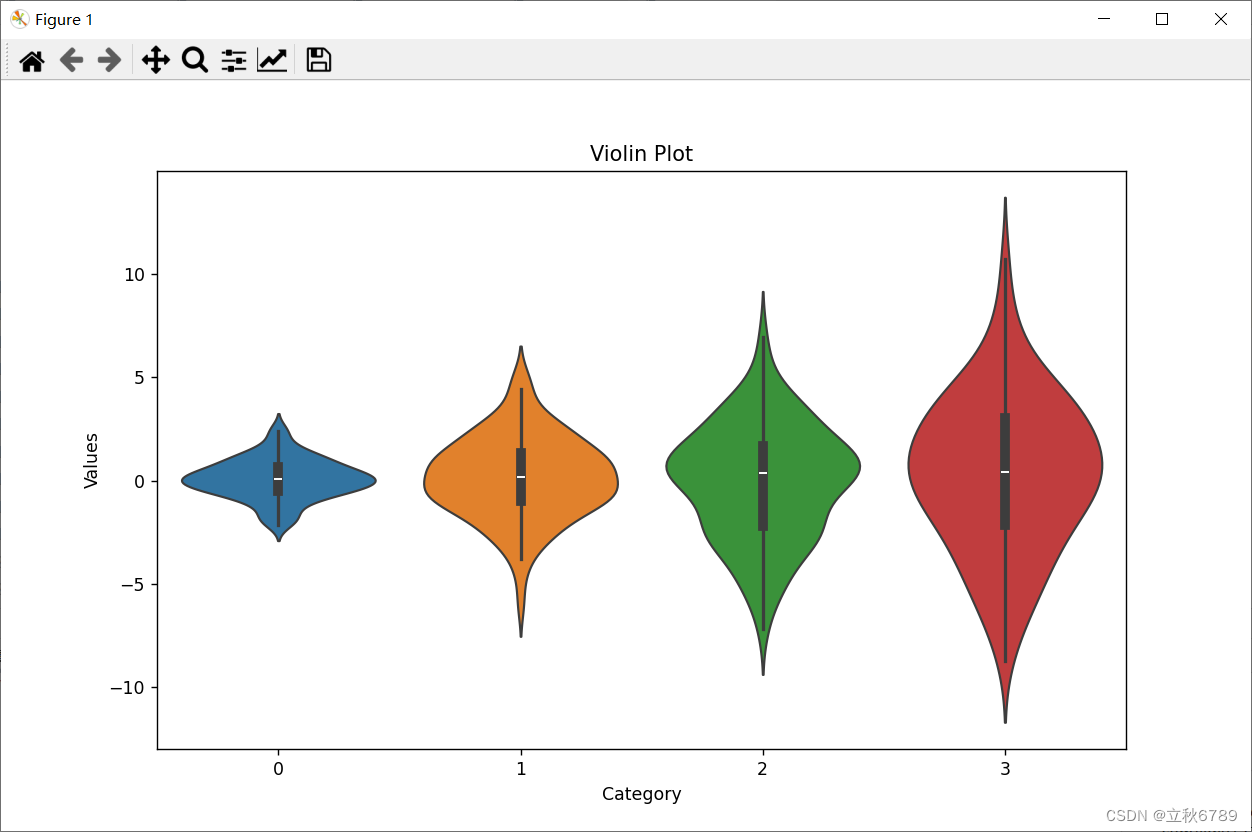
使用python绘制小提琴图
使用python绘制小提琴图 小提琴图效果代码 小提琴图 小提琴图(Violin Plot)是一种结合了箱线图和核密度估计图的图形,用于显示数据分布的情况。它不仅展示了数据的四分位数、最大值和最小值,还通过密度曲线展示了数据的分布形状。…...
)
【C++】6-7 你好,输出的格式控制(三角形)
6-7 你好,输出的格式控制(三角形) 分数 10 全屏浏览 切换布局 作者 向训文 单位 惠州学院 完善程序:输入行数rows(大于0),第一行输出rows个*,接下来每行的*个数减1,直…...

力扣每日一题 6/1
2928.给小朋友们分糖果[简单] 题目: 给你两个正整数 n 和 limit 。 请你将 n 颗糖果分给 3 位小朋友,确保没有任何小朋友得到超过 limit 颗糖果,请你返回满足此条件下的 总方案数 。 示例 1: 输入:n 5, limit 2 …...
决定短视频打开率的要素:成都鼎茂宏升文化传媒公司
在当下这个短视频盛行的时代,无论是个人创作者还是企业品牌,都希望通过短视频平台获得更多的曝光和关注。然而,如何让自己的短视频在众多内容中脱颖而出,吸引用户的点击和观看,成为了摆在我们面前的重要问题。成都…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
