力扣每日一题 6/1
2928.给小朋友们分糖果[简单]
题目:
给你两个正整数 n 和 limit 。
请你将 n 颗糖果分给 3 位小朋友,确保没有任何小朋友得到超过 limit 颗糖果,请你返回满足此条件下的 总方案数 。
示例 1:
输入:n = 5, limit = 2 输出:3 解释:总共有 3 种方法分配 5 颗糖果,且每位小朋友的糖果数不超过 2 :(1, 2, 2) ,(2, 1, 2) 和 (2, 2, 1) 。
示例 2:
输入:n = 3, limit = 3 输出:10 解释:总共有 10 种方法分配 3 颗糖果,且每位小朋友的糖果数不超过 3 :(0, 0, 3) ,(0, 1, 2) ,(0, 2, 1) ,(0, 3, 0) ,(1, 0, 2) ,(1, 1, 1) ,(1, 2, 0) ,(2, 0, 1) ,(2, 1, 0) 和 (3, 0, 0) 。
提示:
1 <= n <= 501 <= limit <= 50
分析:
由提示可知,这道题的数据量并不大,最简单的方法就是暴力,写了三层循环和一个判断,亲测可以通过,只不过时间复杂度较高。
代码实现:
class Solution:def distributeCandies(self, n: int, limit: int) -> int:ls=[]re=0for j in range(n+1):ls.append(j)for i in ls:for q in ls:for w in ls:if i+q+w==n and max(q,i,w)<=limit:# print([i,q,w])re+=1return re 总结:
这道题考的东西不多,主要还是考思维,代码实现并不难。
相关文章:

力扣每日一题 6/1
2928.给小朋友们分糖果[简单] 题目: 给你两个正整数 n 和 limit 。 请你将 n 颗糖果分给 3 位小朋友,确保没有任何小朋友得到超过 limit 颗糖果,请你返回满足此条件下的 总方案数 。 示例 1: 输入:n 5, limit 2 …...
决定短视频打开率的要素:成都鼎茂宏升文化传媒公司
在当下这个短视频盛行的时代,无论是个人创作者还是企业品牌,都希望通过短视频平台获得更多的曝光和关注。然而,如何让自己的短视频在众多内容中脱颖而出,吸引用户的点击和观看,成为了摆在我们面前的重要问题。成都…...

解决通过包管理器下载 Sharp 时遇到的二进制文件下载问题
sharp 是一个流行的 Node.js 库,用于高性能的图片处理。它依赖于预构建的 libvips 二进制文件,这些文件通常是从官方仓库下载的。 但在某些地区的网络环境下,直接下载可能会因为网络限制而失败。 通过在命令行中分别执行以下两行内容即可&a…...

反序输出c++
题目描述 输入n个数,要求程序按输入时的逆序把这n个数打印出来,已知整数不超过100个。也就是说,按输入相反顺序打印这n个数。 输入 输入一行共有n个数,每个数之间用空格隔开。 输出 如题要求:一行,共有n个数&…...
)
C++ 封装线程池(结合QT支持信号机制)
纯C风格线程池 纯C 风格线程池可参考这篇文章 https://llfc.club/category?catid225RaiVNI8pFDD5L4m807g7ZwmF#!aid/2c2IJUcCUOfzEQQRRdOXYIZuCjP 视频教程 相关线程池和并发编程的视频可以看看这个连接: https://www.bilibili.com/video/BV1Xt421H7M7/?vd_s…...
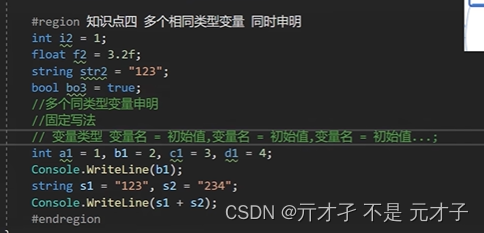
c# 学习教程
打印语句 折叠代码 变量 整形 浮点型 特殊类型...

【ros2】入门
ros2 在机器人控制,无人机飞行控制,自动驾驶领域,ros2可是如日中天的存在。无论是学习其架构设计,还是使用ros2开发机器人,ros2的是一个很错的选择。 安装 在ros2的,推荐“小鱼”的工具 wget http://fishros.com/i…...

网络安全基础技术扫盲篇 — 名词解释之“数据包“
用通俗易懂的话说: 数据包就像是一个信封。当你写信给某个人时,你将内容写在一张纸上,然后将纸叠起来并放入信封中,就形成了一个完整要发送的数据内容。信封上有发件人和收件人的详细地址,还有一些其他必要的信息&…...
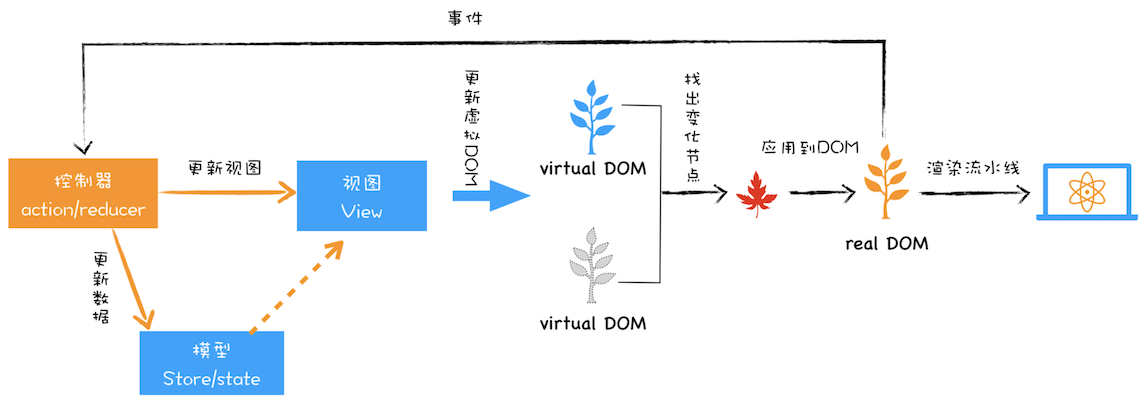
26 _ 虚拟DOM:虚拟DOM和实际的DOM有何不同?
虚拟DOM是最近非常火的技术,两大著名前端框架React和Vue都使用了虚拟DOM,所以我觉得非常有必要结合浏览器的工作机制对虚拟DOM进行一次分析。当然了,React和Vue框架本身所蕴含的知识点非常多,而且也不是我们专栏的重点,…...
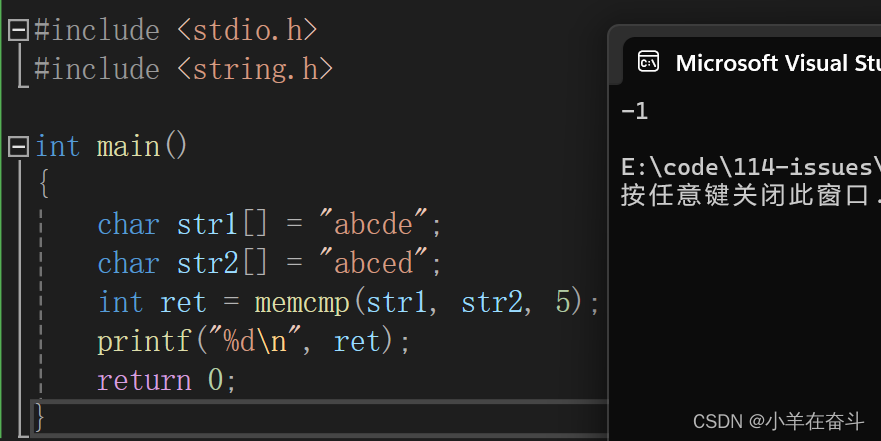
C语言(内存函数)
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记,在这里撰写成文一…...

JVM之【执行引擎】
执行引擎 执行引擎是JVM的核心组件之一,它负责将Java字节码文件转换为机器指令并执行。这一过程涉及多个组成部分,各部分协同工作来完成字节码到机器指令的转换和执行。以下是执行引擎的主要组成部分及其作用: 1. 解释器(Interp…...
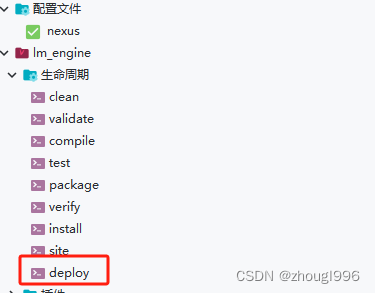
maven部署到私服
方法一:网页上传 1、账号登录 用户名/密码 2、地址 http://自己的ip:自己的端口/nexus 3、查看Repositories列表,选择Public Repositories,确定待上传jar包不在私服中 4、选择3rd party仓库,点击Artifact Upload页签 5、GAV Definition选…...

Android精通值Fragment的使用 —— 不含底层逻辑(五)
1. Fragment 使用Fragment的目标:根据列表动态显示内容,更简洁显示界面、查找界面 eg. 使用新闻列表动态显示新闻 1.1 Fragment的特性 具备生命周期 —— 可以动态地移除一些Fragment必须委托在Activity中使用可以在Activity中进行复用 1.2 Fragmen…...

apache大数据各组件部署搭建(超级详细)
apache大数据数仓各组件部署搭建 第一章 环境准备 1. 机器规划 准备3台服务器用于集群部署,系统建议CentOS7+,2核8G内存 172.19.195.228 hadoop101 172.19.195.229 hadoop102 172.19.195.230 hadoop103 [root@hadoop101 ~]# cat /etc/redhat-release CentOS Linux rele…...

Servlet搭建博客系统
现在我们可以使用Servlet来搭建一个动态(前后端可以交互)的博客系统了(使用Hexo只能实现一个纯静态的网页,即只能在后台自己上传博客)。有一种"多年媳妇熬成婆"的感觉。 一、准备工作 首先创建好项目,引入相关依赖。具体过程在"Servlet的创建"中介绍了。…...
NextJs 渲染篇 - 什么是CSR、SSR、SSG、ISR 和服务端/客户端组件
NextJs 渲染篇 - 什么是CSR、SSR、SSG、ISR 和服务端/客户端组件 前言一. 什么是CSR、SSR、SSG、ISR1.1 CSR 客户端渲染1.2 SSR 服务端渲染1.3 SSG 静态站点生成① 没有数据请求的页面② 页面内容需要请求数据③ 页面路径需要获取数据 1.4 ISR 增量静态再生1.5 四种渲染方式的对…...
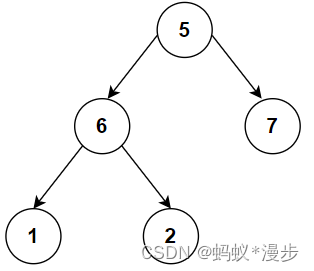
Python 二叉数的实例化及遍历
首先创建一个这样的二叉树,作为我们今天的实例。实例代码在下方。 #创建1个树类型 class TreeNode:def __init__(self,val,leftNone,rightNone):self.valvalself.leftleftself.rightright #实例化类 node1TreeNode(5) node2TreeNode(6) node3TreeNode(7) node4Tre…...
计算 x 的二进制表示中 1 的个数
计算 x 的二进制表示中 1 的个数 代码如下: int func(int x){int countx 0;while (x>0){countx;x x & (x - 1);}return countx;} 完整代码: using System; using System.Collections.Generic; using System.ComponentModel; using System.Dat…...
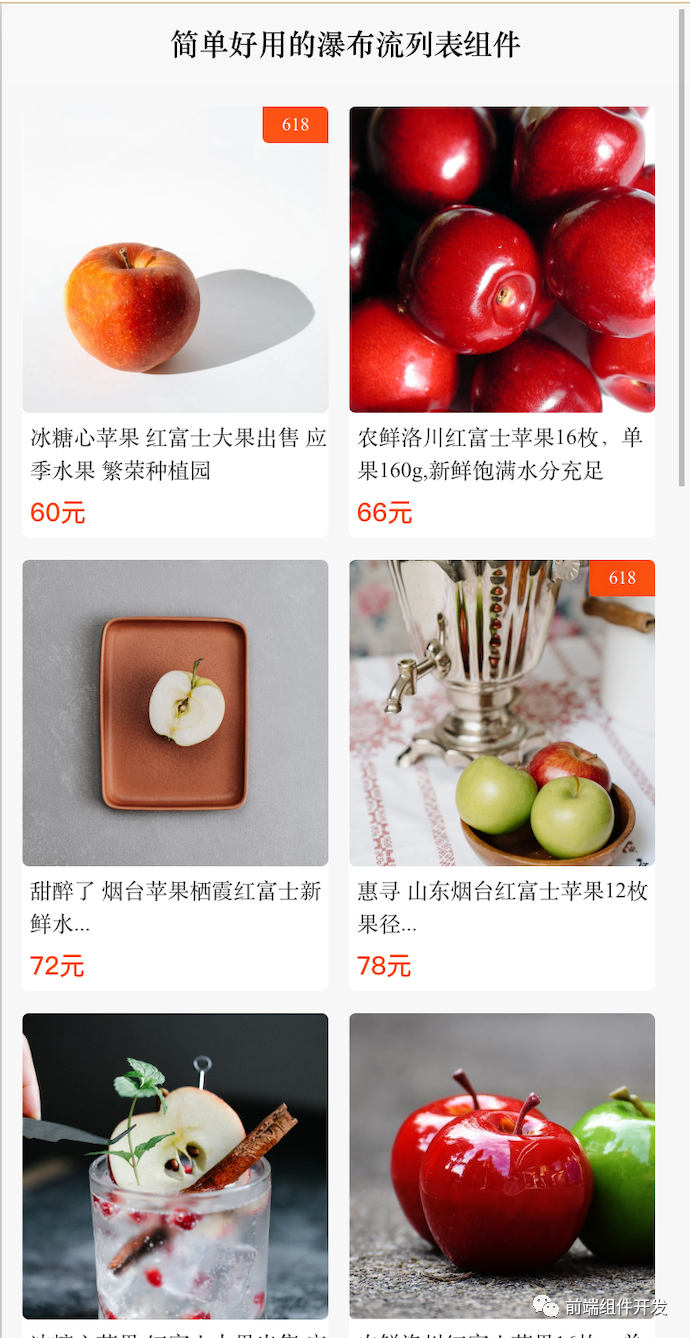
基于Vue的前端瀑布流布局组件的设计与实现
摘要 随着前端技术的不断演进,复杂业务场景和多次迭代后的产品对组件化开发提出了更高的要求。传统的整块应用开发方式已无法满足快速迭代和高效维护的需求。因此,本文将介绍一款基于Vue的瀑布流布局组件,旨在通过组件化开发提升开发效率和降…...
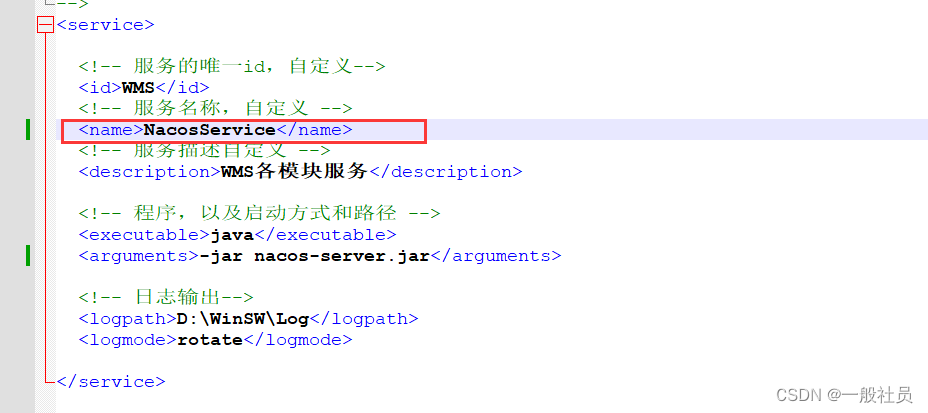
WinSW使用说明
WinSW使用说明 Windows系统下部署多个java程序 场景: 多个java的jar程序,通常来说一个程序使用一个cmd窗口,通过java -jar xxx.jar 命令来运行。这样如果程序多了打开cmd窗口也就多了。 解决: 通过使用WinSW程序,把ja…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
