转换张量形状:`nlc_to_nchw` 函数详解
在深度学习和计算机视觉领域,张量的形状转换是一个常见的操作。本文将详细讲解一个用于形状转换的函数 nlc_to_nchw,它能够将形状为 [N, L, C] 的张量转换为 [N, C, H, W] 的张量。
函数定义
def nlc_to_nchw(x, hw_shape):"""Convert [N, L, C] shape tensor to [N, C, H, W] shape tensor.Args:x (Tensor): The input tensor of shape [N, L, C] before conversion.hw_shape (Sequence[int]): The height and width of output feature map.Returns:Tensor: The output tensor of shape [N, C, H, W] after conversion."""H, W = hw_shapeassert len(x.shape) == 3B, L, C = x.shapeassert L == H * W, 'The seq_len doesn\'t match H, W'return x.transpose(1, 2).reshape(B, C, H, W)
参数解释
-
x (Tensor): 输入张量,其形状为[N, L, C]。其中:N表示批量大小(batch size)。L表示序列长度(sequence length)。C表示通道数(channels)。
-
hw_shape (Sequence[int]): 输出特征图的高度和宽度,为一个包含两个整数的序列(或元组),即[H, W]。其中:H表示高度(height)。W表示宽度(width)。
返回值
Tensor: 转换后的张量,形状为[N, C, H, W]。
详细步骤
-
获取高度和宽度:
H, W = hw_shape从输入参数
hw_shape中提取高度H和宽度W。 -
断言输入张量的形状:
assert len(x.shape) == 3确保输入张量
x的形状是[N, L, C]。 -
提取输入张量的形状参数:
B, L, C = x.shape分别获取批量大小
B、序列长度L和通道数C。 -
验证序列长度是否匹配:
assert L == H * W, 'The seq_len doesn\'t match H, W'确保序列长度
L等于高度H乘以宽度W。这是必要条件,因为序列长度需要与特征图的总像素数匹配。 -
转换形状:
return x.transpose(1, 2).reshape(B, C, H, W)通过
transpose和reshape操作,将输入张量从[N, L, C]转换为[N, C, H, W]:x.transpose(1, 2)将张量的第二个和第三个维度交换,形状变为[N, C, L]。reshape(B, C, H, W)将张量重新调整形状为[N, C, H, W]。
示例
假设有一个形状为 [2, 6, 3] 的输入张量 x,其中 N=2, L=6, C=3。给定的 hw_shape 为 [2, 3],表示高度 H=2 和宽度 W=3。
import torchx = torch.rand(2, 6, 3) # 创建一个形状为 [2, 6, 3] 的随机张量
hw_shape = [2, 3] # 定义高度和宽度output = nlc_to_nchw(x, hw_shape) # 调用函数
print(output.shape) # 输出张量的形状为 [2, 3, 2, 3]
运行上述代码后,输出张量的形状将为 [2, 3, 2, 3],符合预期的 [N, C, H, W] 形状。
总结
通过 nlc_to_nchw 函数,我们可以轻松地将形状为 [N, L, C] 的张量转换为 [N, C, H, W] 的张量。这在处理图像数据和构建神经网络时非常有用,因为不同的层和操作可能要求特定的张量形状。理解和掌握这些基本的张量操作是深度学习实践中的重要技能。
相关文章:

转换张量形状:`nlc_to_nchw` 函数详解
在深度学习和计算机视觉领域,张量的形状转换是一个常见的操作。本文将详细讲解一个用于形状转换的函数 nlc_to_nchw,它能够将形状为 [N, L, C] 的张量转换为 [N, C, H, W] 的张量。 函数定义 def nlc_to_nchw(x, hw_shape):"""Convert …...

「架构」云上自动化运维及其应用
随着云计算的普及,自动化运维成为企业提升运营效率和降低成本的关键。本文通过分析一家中型企业实施云上自动化运维(CloudOps)的案例,探讨了自动化监控、配置管理和持续集成/持续部署(CI/CD)三个核心模块的实际应用。文章详细阐述了每个模块的技术选型、实施原因、优缺点…...

分布式和集群的区别
分布式系统(Distributed System)和集群(Cluster)是两个经常被提及的计算机科学概念,它们在提高系统性能和可靠性方面都扮演着重要角色,很多同学会觉得这俩个是同一种东西,但事实上它们之间有着本…...

最新h5st(4.7.2)参数分析与纯算法还原(含算法源码)
文章目录 1. 写在前面2. 加密分析3. 算法还原 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python…...

Spark大数据 掌握RDD的创建
在Apache Spark中,弹性分布式数据集(Resilient Distributed Dataset,简称RDD)是一个核心的数据结构,用于表示不可变、可分区、可并行操作的元素集合。理解并掌握RDD的创建是使用Spark进行大数据处理的关键步骤之一。 …...

Chrome谷歌浏览器如何打开不安全页面的禁止权限?
目录 一、背景二、如何打开不安全页面被禁止的权限?2.1 第一步,添加信任站点2.2 第二步,打开不安全页面的权限2.3 结果展示 一、背景 在开发过程中,由于测试环境没有配置 HTTPS 请求,所以谷歌浏览器的地址栏会有这样一…...
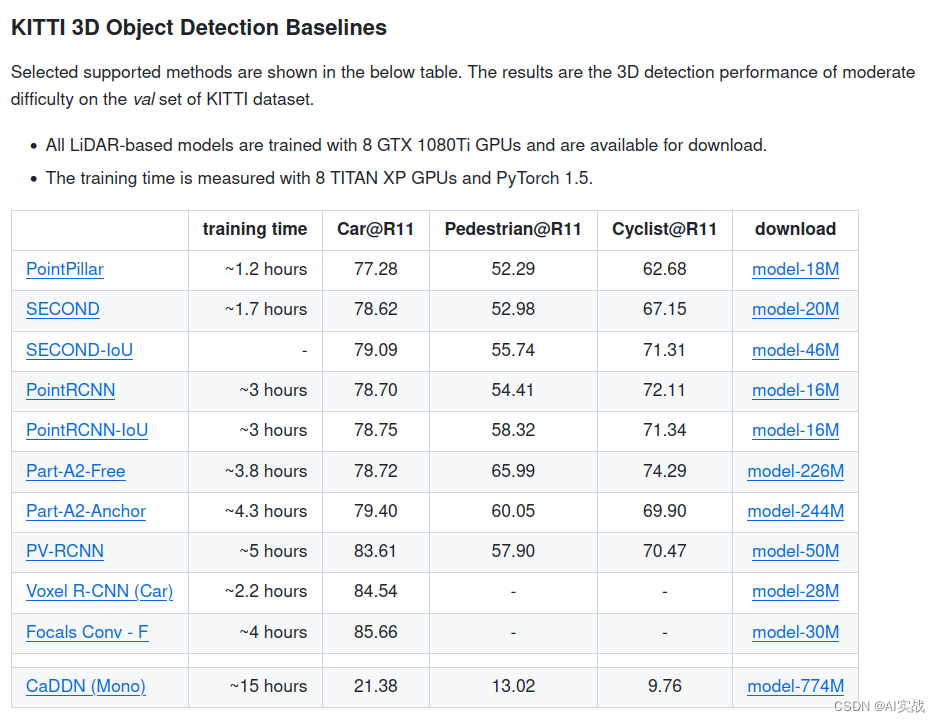
3D目标检测入门:探索OpenPCDet框架
前言 在自动驾驶和机器人视觉这两个飞速发展的领域中,3D目标检测技术扮演着核心角色。随着深度学习技术的突破性进展,3D目标检测算法的研究和应用正日益深入。OpenPCDet,这个由香港中文大学OpenMMLab实验室精心打造的开源工具箱,…...

JS异步编程
目录 概念定时器Promise对象概念 单线程模型指的是,JavaScript 只在一个线程上运行。也就是说,JavaScript 同时只能执行一个任务,其他任务都必须在后面排队等待。JavaScript 只在一个线程上运行,不代表 JavaScript 引擎只有一个线程。事实上,JavaScript 引擎有多个线程,…...
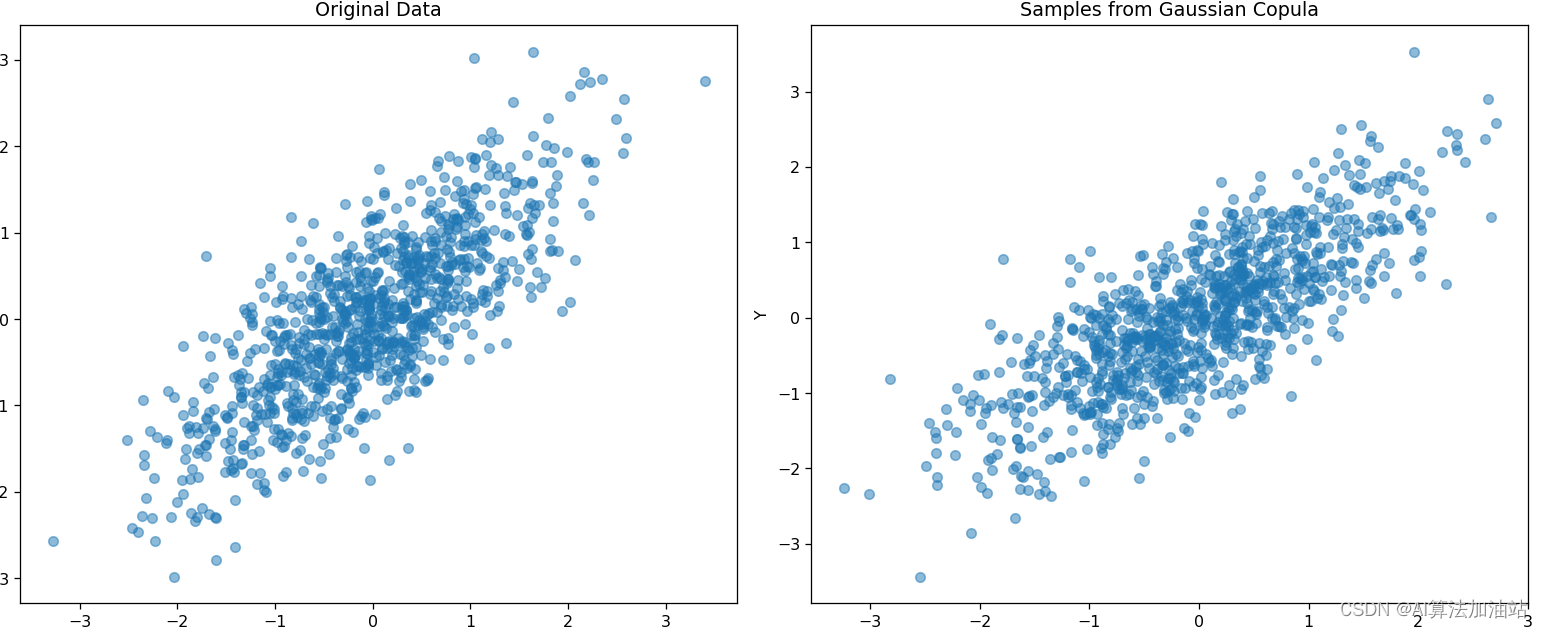
多元联合分布建模 Copula python实例
多元联合分布建模 Copula python实例 目录 库安装 实例可视化代码 库安装 pip install copulas 实例可视化代码 import numpy as np import pandas as pd from copulas.multivariate import GaussianMultivariate# Generate some example data np.random.seed(42) data = …...

单号日入50+,全自动挂机赚钱
大家好!今天我为大家精心挑选了一个极具潜力的副业项目——“游戏工作室自由之刃2:单号日入50,全自动挂机赚钱”。 传奇游戏,无疑是许多人心中那段青春时光的珍贵回忆。 即便是其手游版本,也依旧保持着极高的热度和人…...
LabVIEW老程序功能升级:重写还是改进?
概述:面对LabVIEW老程序的功能升级,开发者常常面临重写与改进之间的选择。本文从多个角度分析两种方法的利弊,并提供评估方法和解决思路。 重写(重新开发)的优势和劣势: 优势: 代码清晰度高&a…...
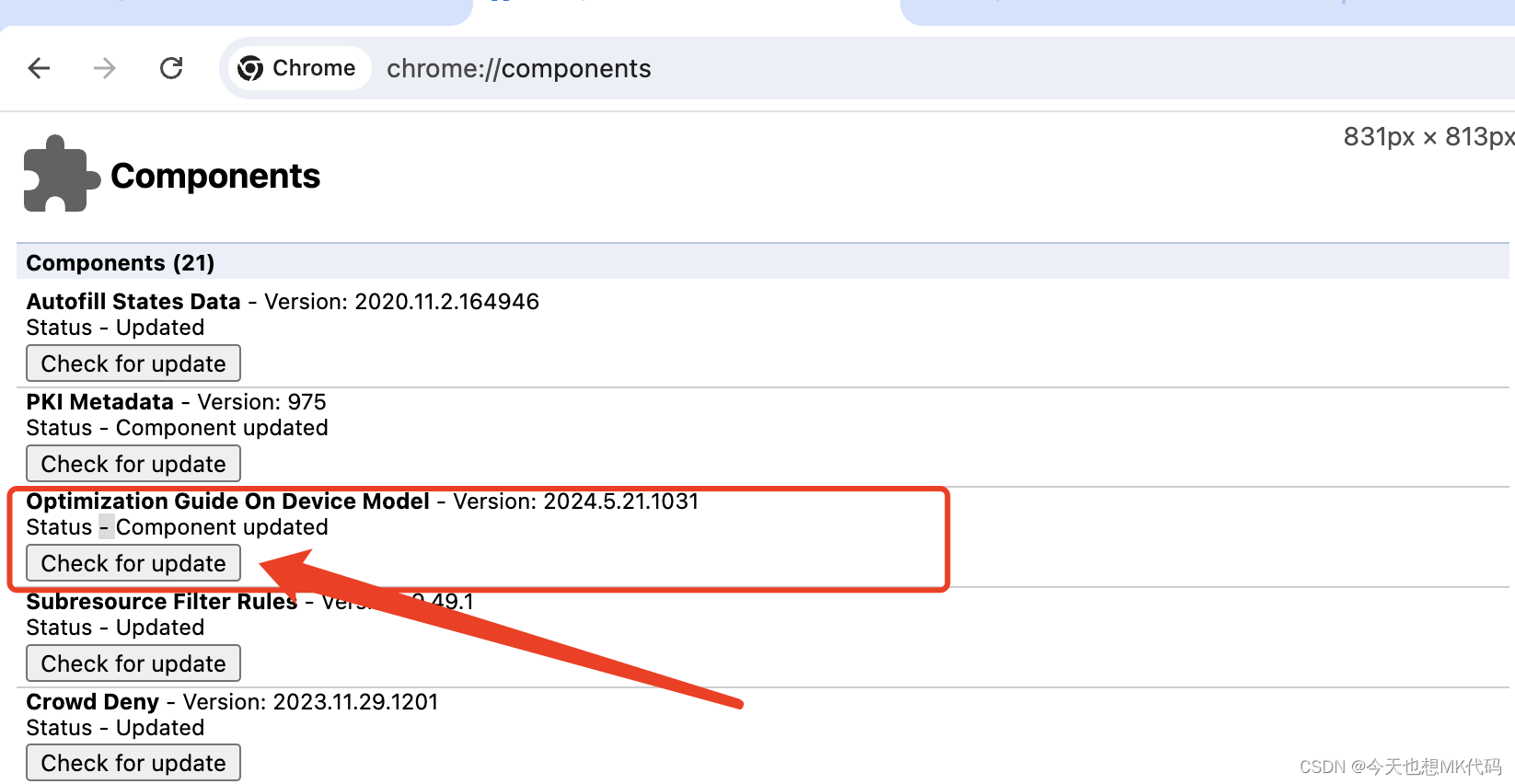
chrome谷歌浏览器开启Gemini Nano模型
前提 确保您的操作系统语言设置为英语(美国) 可能还需要将 Chrome 浏览器的语言更改为英语(美国)。 下载dev或Canary版本Chrome Chrome Canary Chrome Dev 注意:确认您的版本高于 127.0.6512.0。 其中一个Chrome版本…...
C语言王国——内存函数
目录 1 memcpy函数 1.1 函数表达式 1.2 函数模拟 2 memmove函数 2.1 函数的表达式 2.2 函数模拟 3 memset函数 3.1 函数的表达式 3.2 函数的运用 4 memcmp函数 4.1函数的表达式: 4.2 函数的运用 5 结论 接上回我们讲了C语言的字符和字符串函数&#…...
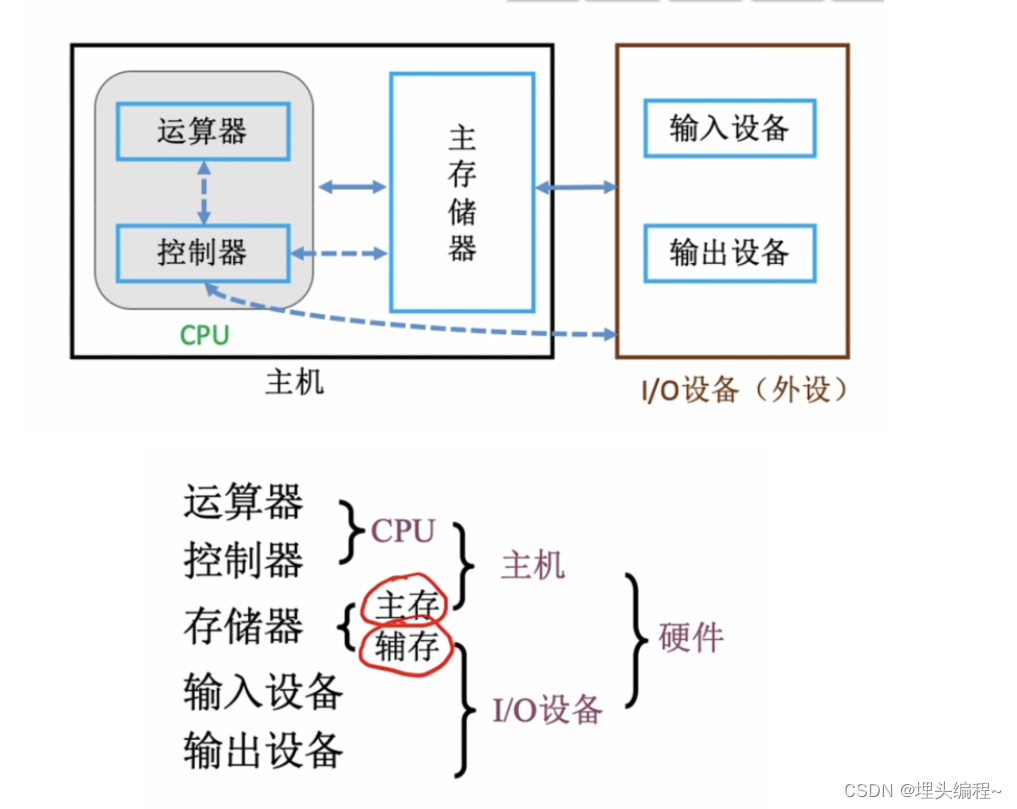
【计算机组成原理】1.1计算机的软硬件组成(记录学习计算机组成原理)
文章目录 1.早期的冯诺依曼机2.早期冯诺依曼机的基本运行框图3.早期冯诺依曼机的特点4.现代计算机的结构5. 小结 本次及以后有关于计算机组成原理的文章,旨在做学习时的记录和知识的分享。不论是应对期末考试,还是考研都是很有帮助的。希望大家多多支持更…...
Qt xml学习之calculator-qml
1.功能说明:制作简易计算器 2.使用技术:qml,scxml 3.项目效果: 4.qml部分: import Calculator 1.0 //需要引用对应类的队友版本 import QtQuick 2.12 import QtQuick.Window 2.12 import QtQuick.Controls 1.4 import QtScxml…...
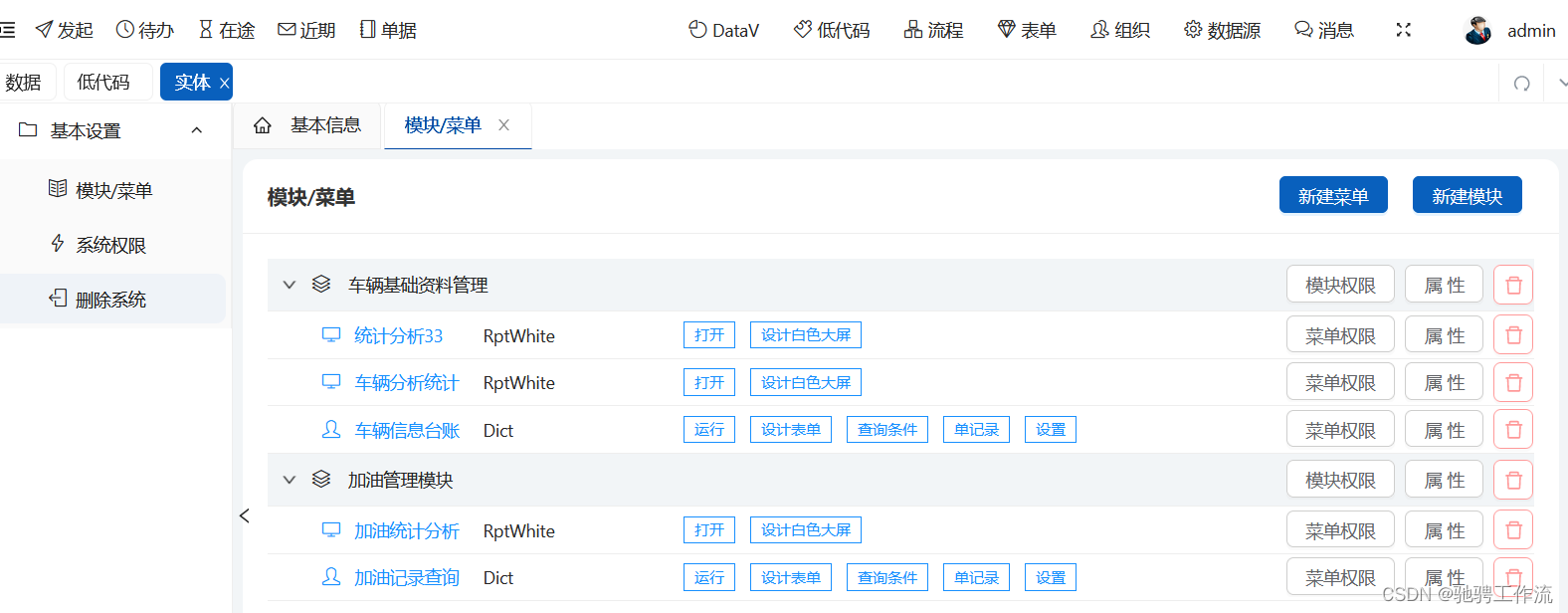
低代码开发系统是什么?它有那些部分组成?
低代码开发系统是什么?它有那些部分组成? 一、引言 在当今快速变化的商业环境中,企业对于快速响应市场需求、降低开发成本和提高开发效率的需求日益增强。低代码开发系统(Low-Code Development Platform)应运而生&am…...
2024年西安交通大学程序设计竞赛校赛
2024年西安交通大学程序设计竞赛校赛 文章目录 2024年西安交通大学程序设计竞赛校赛D瑟莉姆的宴会E: 雪中楼I: 命令行(待补)J:最后一块石头的重量(待补)K: 崩坏:星穹铁道(待补)M:生命游戏N: 圣诞树 D瑟莉姆的宴会 解题思路: …...

【学习Day5】操作系统
✍🏻记录学习过程中的输出,坚持每天学习一点点~ ❤️希望能给大家提供帮助~欢迎点赞👍🏻收藏⭐评论✍🏻指点🙏 学习编辑文章的时间不太够用,先放思维导图,后续复习完善细节。...
学习小记录——python函数的定义和调用
今日小好运,未来有好运。🎁💖🫔 分享个人学习的小小心意,一起来看看吧 函数的定义 函数通常来说就是带名字的代码块,用于完成具体的工作,需要使用的时候调用即可,这不仅提高代码的…...
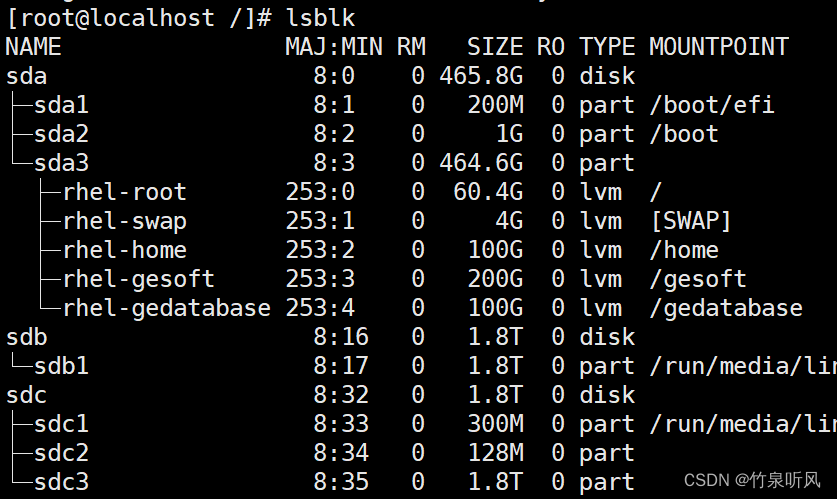
RHEL7.9修改分区
系统RHEL7.9 他因为安装软件,需要修改分区 进入超级用户root,输入lsblk 查看分区,可见465.8G系统盘sda下有三个物理卷,其中sda3下/home有410.6G,需要这部分拆分出200G软件和100G的数据库分区 备份/home 目录下文件 c…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
