【机器学习】逻辑回归:原理、应用与实践


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 逻辑回归:原理、应用与实践
- 引言
- 1. 逻辑回归基础
- 1.1 基本概念
- 1.2 Sigmoid函数
- 2. 模型构建
- 2.1 线性决策边界
- 2.2 参数估计
- 3. 损失函数与优化
- 3.1 交叉熵损失函数
- 3.2 优化算法
- 4. 多分类逻辑回归
- 5. 实践应用与案例分析
- 5.1 应用领域
- 5.2 案例分析
- 6. 逻辑回归的局限与挑战
- 7. 结论
逻辑回归:原理、应用与实践
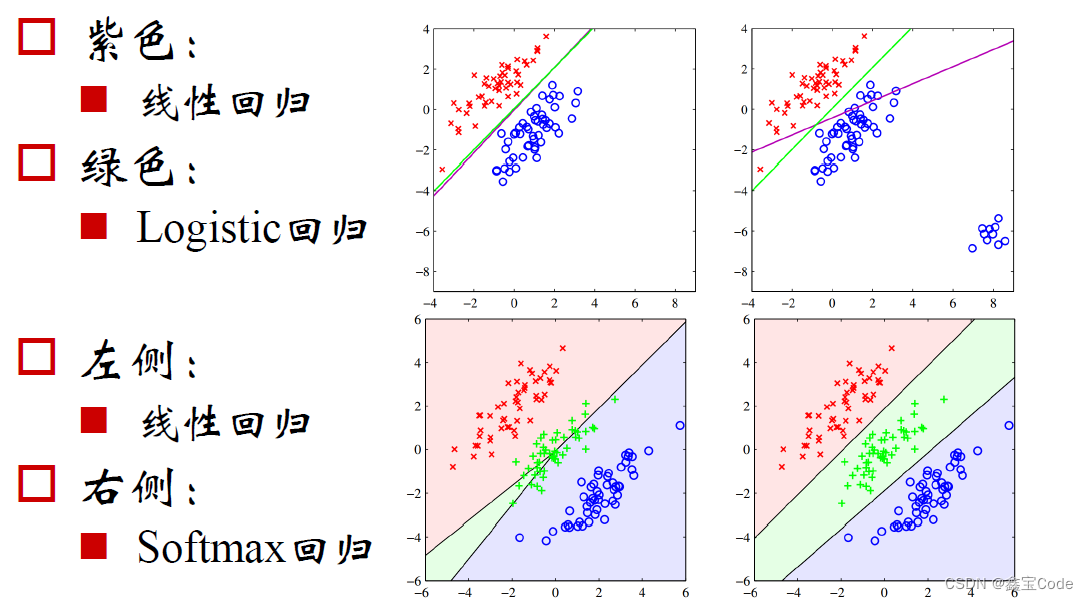
引言
逻辑回归(Logistic Regression)是一种广泛应用于分类问题的统计学方法,尽管其名称中含有“回归”二字,但它实际上是一种用于解决二分类或多分类问题的线性模型。逻辑回归通过使用逻辑函数(通常为sigmoid函数)将线性模型的输出映射到概率空间,从而预测某个事件发生的概率。本文将深入探讨逻辑回归的理论基础、模型构建、损失函数、优化算法以及实际应用案例,并简要介绍其在机器学习领域的地位和局限性。
1. 逻辑回归基础
1.1 基本概念
逻辑回归主要用于处理因变量为离散型数据的问题,尤其是二分类问题,如判断一个用户是否会购买某产品、一封邮件是否为垃圾邮件等。其核心思想是通过建立输入特征与输出类别之间的逻辑关系模型,来预测输出为某一类别的概率。
1.2 Sigmoid函数
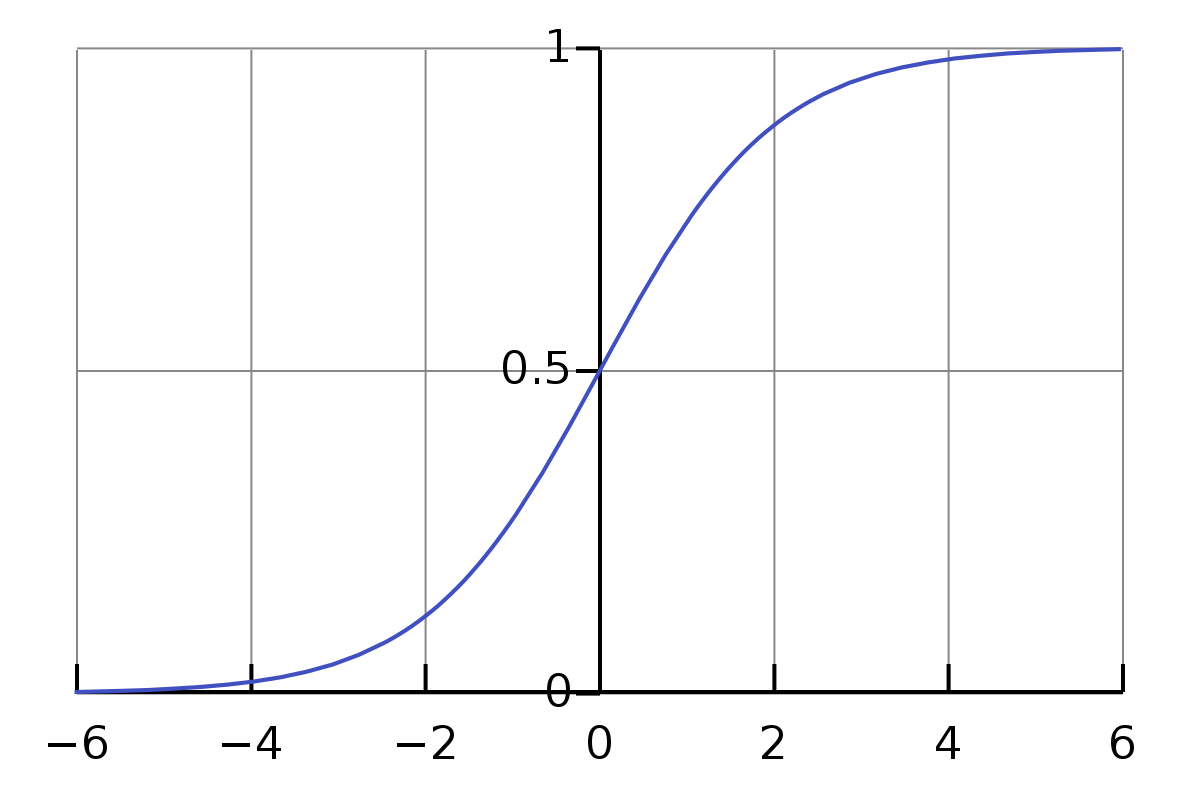
Sigmoid函数是逻辑回归中的关键组件,其表达式为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
该函数将线性组合 z = θ T x z = \theta^T x z=θTx(其中$ \theta $为模型参数,(x)为输入特征向量)的输出映射到(0, 1)之间,可以解释为事件发生的概率。
2. 模型构建
2.1 线性决策边界
逻辑回归模型的形式化表达为:
P ( Y = 1 ∣ X = x ) = σ ( θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n ) P(Y=1|X=x) = \sigma(\theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n) P(Y=1∣X=x)=σ(θ0+θ1x1+θ2x2+...+θnxn)
其中, ( P ( Y = 1 ∣ X = x ) (P(Y=1|X=x) (P(Y=1∣X=x)表示给定特征(x)时,事件发生的概率;(\theta_i)为模型参数,(\theta_0)为截距项。
2.2 参数估计
逻辑回归通过极大似然估计(MLE)来确定模型参数。具体来说,是找到一组参数(\theta),使得训练数据的似然性最大化。
3. 损失函数与优化
3.1 交叉熵损失函数
逻辑回归常用的损失函数是交叉熵损失(Cross-Entropy Loss),它衡量了模型预测概率分布与真实概率分布的差异。对于二分类问题,损失函数定义为:
J ( θ ) = − 1 m ∑ i = 1 m [ y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) ] J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y_i \log(p_i) + (1-y_i) \log(1-p_i)] J(θ)=−m1i=1∑m[yilog(pi)+(1−yi)log(1−pi)]
其中,(m)是样本数量,(y_i)是真实标签,(p_i)是模型预测的概率。
3.2 优化算法
常见的优化算法有梯度下降法及其变种(如批量梯度下降、随机梯度下降、小批量梯度下降)和拟牛顿法等。这些算法通过迭代更新模型参数,以逐步降低损失函数值,达到参数最优解。
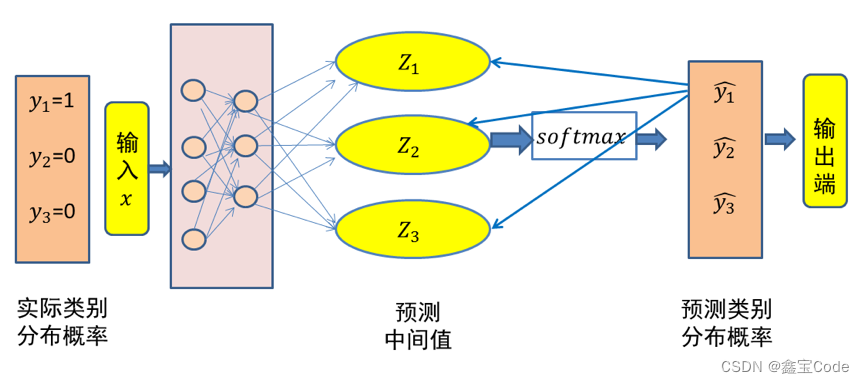
4. 多分类逻辑回归
对于多分类问题,逻辑回归可以通过两种主要方式扩展:一对一(One-vs-One, OvO)和一对多(One-vs-All, OvA)。每种方法都有其适用场景和优缺点。
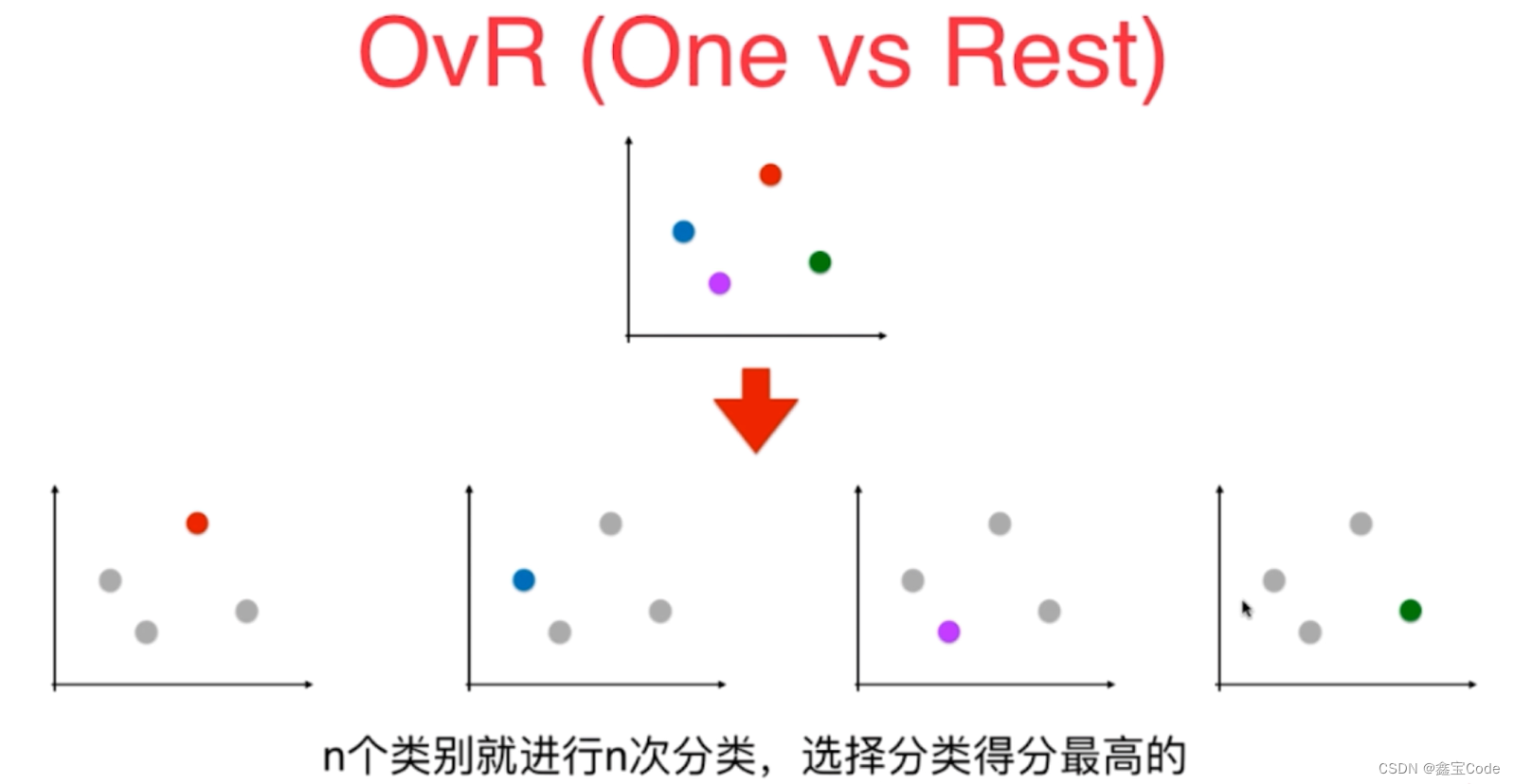
5. 实践应用与案例分析
5.1 应用领域
逻辑回归因其简单有效,在金融风控、医疗诊断、市场营销等多个领域有着广泛应用。例如,在银行信用评估中,逻辑回归模型可以用来预测客户违约的可能性。
5.2 案例分析
考虑一个简化版的银行贷款申请预测模型。通过收集申请人的年龄、收入、信用评分等特征,利用逻辑回归模型预测申请人是否会违约。通过特征工程、模型训练、交叉验证和调参等步骤,最终得到一个具有较高预测准确率的模型,为银行审批贷款提供决策支持。
首先,请确保安装了scikit-learn库。如果未安装,可以通过pip命令安装:
pip install scikit-learn
然后,你可以使用以下Python代码来实现逻辑回归:
# 导入必要的库
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.preprocessing import StandardScaler# 加载数据集,这里以鸢尾花数据集为例,但鸢尾花是多分类问题,我们简化为二分类
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, :2] # 只取前两列特征,简化为二维问题
y = (iris.target != 0).astype(int) # 将目标转换为二分类问题(0和1)# 数据预处理:标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)# 创建逻辑回归模型实例
logreg = LogisticRegression(max_iter=10000)# 训练模型
logreg.fit(X_train, y_train)# 预测测试集结果
y_pred = logreg.predict(X_test)# 输出模型性能指标
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
print("Precision:", metrics.precision_score(y_test, y_pred))
print("Recall:", metrics.recall_score(y_test, y_pred))# 输出模型系数和截距
print("Coefficients:", logreg.coef_)
print("Intercept:", logreg.intercept_)
这段代码演示了如何使用逻辑回归进行二分类任务的基本流程。注意,真实项目中可能需要更复杂的数据预处理和特征工程,以及更细致的模型调整和验证。此外,逻辑回归默认使用的是L2正则化,可以通过调整参数来改变正则化类型或强度。
6. 逻辑回归的局限与挑战
尽管逻辑回归在众多领域表现良好,但其也有一定的局限性:
- 线性假设:逻辑回归假设特征与目标变量间存在线性关系,对于非线性关系可能无法很好地建模。
- 处理大规模特征或高维数据时可能会遇到过拟合问题。
- 对于类别极度不均衡的数据集,需要特别处理以避免模型偏向多数类。
7. 结论
逻辑回归作为经典的机器学习算法之一,凭借其简单、直观且易于实现的特点,在分类任务中依然保持重要地位。尽管面临一些局限性,通过引入正则化、特征选择、非线性变换等手段,逻辑回归能够适应更复杂的实际问题。随着深度学习等新技术的发展,逻辑回归也被融合进更复杂的模型结构中,继续发挥其独特价值。理解逻辑回归不仅有助于掌握基本的机器学习原理,也是深入探索现代机器学习技术的坚实基础。


相关文章:

【机器学习】逻辑回归:原理、应用与实践
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 逻辑回归:原理、应用与实践引言1. 逻辑回归基础1.1 基本概念1.2 Sig…...

C++:list模拟实现
hello,各位小伙伴,本篇文章跟大家一起学习《C:list模拟实现》,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 ! 如果本篇文章对你有帮助,还请各位点点赞!…...
植物大战僵尸杂交版全平台 PC MAC 安卓手机下载安装详细图文教程
最近植物大战僵尸杂交版非常的火,好多小伙伴都想玩一玩,但作者只分享了 win 版,像手机还有MAC电脑都没有办法安装,身为 MAC 党当然不能放弃,经过一番折腾,也是成功在所有平台包括手机和MAC电脑都成功安装上…...

发送Http请求的两种方式
说明:在项目中,我们有时会需要调用第三方接口,获取调用结果,来实现自己的业务逻辑。调用第三方接口,通常是双方确定好,由对方开放一个接口,需要我们根据他们提供的接口文档,组装Http…...
【算法训练记录——Day23】
Day23——二叉树Ⅸ 669.修剪二叉搜索树108.将有序数组转换为二叉搜索树538.把二叉搜索树转换为累加树 今日内容: ● 669.修剪二叉搜索树 ● 108.将有序数组转换为二叉搜索树 ● 538.把二叉搜索树转换为累加树 ● 总结篇 669.修剪二叉搜索树 思路:主要是…...
【wiki知识库】04.SpringBoot后端实现电子书的增删改查以及前端界面的展示
📝个人主页:哈__ 期待您的关注 目录 一、🔥今日内容 二、🌏前端页面的改造 2.1新增电子书管理页面 2.2新增路由规则 2.3修改the-header代码 三、🚗SpringBoot后端Ebook模块改造 3.1增加电子书增/改接口 3.1.…...

NTLM Relay Gat:自动化NTLM中继安全检测工具
关于NTLM Relay Gat NTLM Relay Gat是一款功能强大的NTLM中继威胁检测工具,该工具旨在利用Impacket工具套件中的ntlmrelayx.py脚本在目标环境中实现NTLM中继攻击风险检测,以帮助研究人员确定目标环境是否能够抵御NTLM中继攻击。 功能介绍 1、多线程支持…...
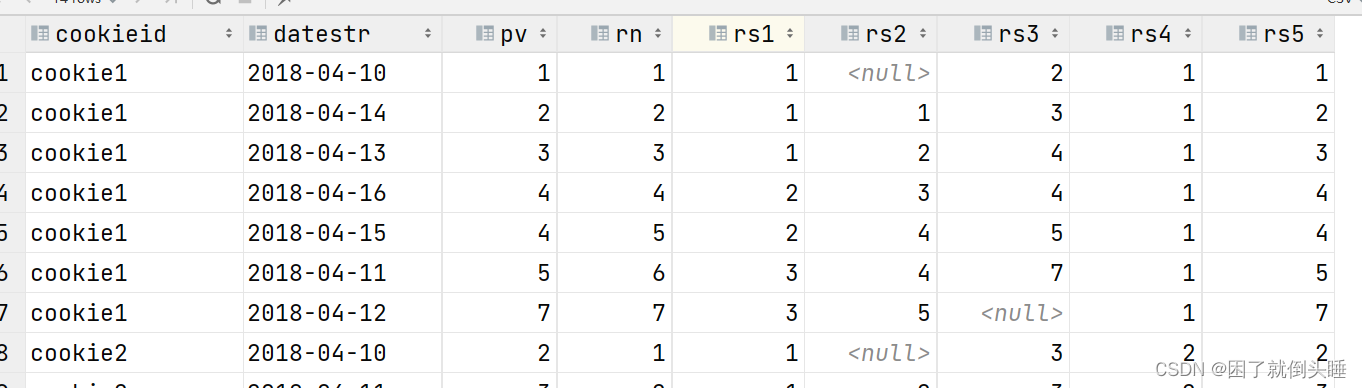
摸鱼大数据——Hive函数14
14、开窗(开列)函数 官网链接:Window Functions - Apache AsterixDB - Apache Software Foundation 14.1 基础使用 开窗函数格式: 开窗函数 over(partition by 分组字段名 [order by 排序字段名 asc|desc] [rows between 开窗开始 and 开窗结束]) partition b…...

elasticsearch的常规操作--增删改查和批量处理
1、_cat 查询 GET /_cat/nodes: 查看所有节点 GET /_cat/health: 查看es 健康状况 GET /_cat/master: 查看主节点 GET /_cat/indices:查看所有索引show databases; 2、索引一个文档(保存) 保存一个数据&…...
盘点2024年还在活跃发版的开源私有网盘项目附源码链接
时不时的会有客户上门咨询,丰盘ECM是不是开源项目,源码在哪里可以下载;如果需要和内部其他系统做集成,购买商业版的话,能否提供源代码做二次开发呢,等等诸多问题。 这里做个统一回复,丰盘ECM产…...
MySQL 使用方法以及教程
一、引言 MySQL是一个流行的开源关系型数据库管理系统(RDBMS),广泛应用于Web开发、数据分析等领域。它提供了高效、稳定的数据存储和查询功能。同时,Python作为一种强大的编程语言,也提供了多种与MySQL交互的库&#…...

算法学习笔记——二进制
二进制 负数的十进制转二进制数(-2 -> 1110): 正数 - 1,再取反,得到负数的二进制。 例如:-2 :0010 -> 0010 - 1 -> 0001 -> 取反 -> 1110 负数的二进制转十进制(…...
计算机网络介绍
计算机网络介绍 概述网络概述相关硬件 链路层VLAN概念VLAN 特点VLAN 的划分帧格式端口类型原理 STP概念特点原理 Smart Link概念特点组网 网络层ARP概念原理 IP概念版本IP 地址 IPv4IP 地址数据报格式 IPv6特点IP 地址数据报格式 ICMP概念分类报文格式 VRRP概念原理报文格式 OS…...
解锁数据宝藏:高效查找算法揭秘
代码下载链接:https://gitee.com/flying-wolf-loves-learning/data-structure.git 目录 一、查找的原理 1.1 查找概念 1.2 查找方法 1.3平均查找长度 1.4顺序表的查找 1.5 顺序表的查找算法及分析 1.6 折半查找算法及分析 1.7 分块查找算法及分析 1.8 总结…...
利用EasyCVR视频智能监控技术,构建智慧化考场监管体系
随着科技的进步,视频监控在各个领域的应用越来越广泛,其中在考场中的应用尤为显著。视频监控不仅能够提高考场的监管水平,确保考试的公平、公正和公开,还能有效预防和打击作弊行为,为考生营造一个良好的考试环境。 传…...

深度解析:速卖通618风控下自养号测评的技术要点
速卖通每年的618大促活动平台的风控都会做升级,那相对的测评技术也需要进行相应的做升级,速卖通618风控升级后,自养号测评需要注意以下技术问题,以确保测评 的稳定性和安全性: 一、物理环境 1. 硬件参数伪装&#x…...

国产算力——沐曦GPU性能及应用
沐曦集成电路(上海)有限公司(简称“沐曦”)成立于2020年9月,专注于为异构计算提供全栈GPU芯片及解决方案,满足数据中心对“高性能”、“高能效”及“高通用性”的算力需求。 产品系列 沐曦构建了全栈高性…...
贪心算法拓展(反悔贪心)
相信大家对贪心算法已经见怪不怪了,但是一旦我们的决策条件会随着我们的步骤变化,我们该怎么办呢?有没有什么方法可以反悔呢? 今天就来讲可以后悔的贪心算法,反悔贪心。 https://www.luogu.com.cn/problem/CF865Dhttp…...

在spring框架的基础上自定义autowired注解
在Spring框架的基础上自定义Autowired注解是不可能的,因为注解本身是Java语言的一部分,并且Autowired是Spring框架提供的注解,用于实现自动装配。但是,你可以创建自己的注解,并结合Spring框架的扩展机制来实现类似的功…...

2005NOIP普及组真题 3. 采药
线上OJ: [05NOIP普及组] 采药 核心思想: 1、题与 2006 年普及组第2题《开心的金明》一样,考察的都是01背包。 2、直接套用01背包的一阶模板即可 a、限定时间看成背包总容量m b、每件物品的采药时间 v 看成占用背包的体积 c、每件物品的价格w作为该物品的…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
