乡村振兴与农业科技创新:加大农业科技研发投入,推动农业科技创新,促进农业现代化和美丽乡村建设
一、引言
在当代中国,乡村振兴已成为国家发展的重要战略之一。作为国民经济的基础,农业的发展直接关系到国家的稳定和人民的福祉。随着科技的不断进步,农业科技创新在推动农业现代化和美丽乡村建设中发挥着越来越重要的作用。本文旨在探讨如何通过加大农业科技研发投入,推动农业科技创新,进而促进农业现代化和美丽乡村建设。

二、农业科技创新的重要性
(一)提升农业生产效率
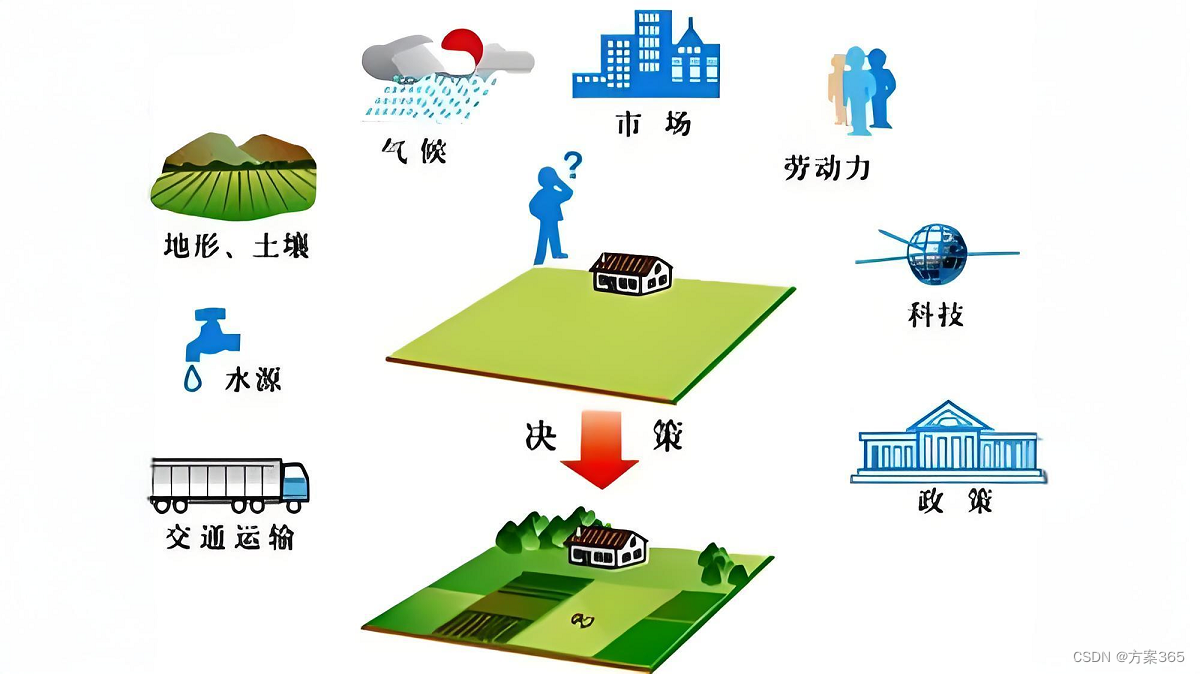
农业科技创新能够通过引进新品种、新技术和新方法,提高农业生产效率。例如,通过基因编辑技术培育出抗病、抗虫、高产的作物品种,能够减少农药和化肥的使用,降低生产成本,提高产量和品质。此外,智能化、自动化的农业机械设备的应用,也能够大大提高农业生产效率,减轻农民的劳动强度。
(二)促进农业可持续发展
农业科技创新还能够促进农业可持续发展。通过发展生态农业、循环农业等新型农业模式,能够减少农业生产对环境的污染和破坏,保护生态环境。同时,农业科技创新还能够推动农业资源的合理利用和高效利用,提高农业资源的利用效率,促进农业可持续发展。
(三)增强农业竞争力
在全球化的背景下,农业竞争日益激烈。农业科技创新能够提升农产品的品质和附加值,增强农产品的市场竞争力。通过引进先进的生产技术和管理方法,能够提高农产品的品质和安全性,满足消费者对高品质农产品的需求。同时,农业科技创新还能够推动农业产业的转型升级,培育新的经济增长点,增强农业的综合竞争力。
三、加大农业科技研发投入的必要性
(一)适应农业现代化的需求
随着农业现代化的不断推进,农业生产对科技的需求越来越高。加大农业科技研发投入,能够满足农业现代化的需求,推动农业科技创新和进步。只有不断引进新技术、新品种和新方法,才能够提高农业生产的效率和质量,推动农业现代化的发展。
(二)推动农业科技创新
农业科技创新是推动农业现代化和美丽乡村建设的关键。然而,农业科技创新需要投入大量的资金和人力资源。加大农业科技研发投入,能够为农业科技创新提供充足的资金支持和人才保障,推动农业科技创新的深入开展。通过加强农业科技研发机构和企业的建设,加强产学研合作,推动农业科技成果的转化和应用,实现农业科技创新的可持续发展。
(三)促进乡村经济发展
农业是乡村经济的主体。加大农业科技研发投入,推动农业科技创新和进步,能够带动乡村经济的发展。通过引进新技术、新品种和新方法,能够提高农产品的附加值和市场竞争力,增加农民的收入。同时,农业科技创新还能够推动农业产业的转型升级,培育新的经济增长点,促进乡村经济的繁荣和发展。
四、推动农业科技创新的策略
(一)加强农业科技研发机构和企业的建设
要加强农业科技研发机构和企业的建设,提高农业科技研发的水平和能力。政府应该加大对农业科技研发机构和企业的支持力度,鼓励企业增加对农业科技研发的投入,加强产学研合作,推动农业科技成果的转化和应用。
(二)培养农业科技人才
要加强农业科技人才的培养和引进工作。通过加强农业科技教育和培训,提高农民的科学素质和技能水平。同时,要积极引进国内外优秀的农业科技人才,为农业科技创新提供人才保障。
(三)完善农业科技服务体系
要完善农业科技服务体系,为农民提供全方位的农业科技服务。政府应该加强农业科技推广和普及工作,建立农业科技服务平台和专家库,为农民提供技术咨询、培训和指导等服务。同时,要鼓励农业科技服务机构和企业的发展,提高农业科技服务的质量和效率。
“方案365”全新整理乡村振兴规划设计、智慧文旅、智慧园区、数字乡村-智慧农业、智慧城市、数据治理、智慧应急、数字孪生、乡村振兴、智慧乡村、元宇宙、数据中台、智慧矿山、城市生命线、智慧水利、智慧校园、智慧工地、智慧农业、智慧旅游等300+行业全套解决方案。
五、结语
乡村振兴与农业科技创新密不可分。加大农业科技研发投入,推动农业科技创新和进步,是促进农业现代化和美丽乡村建设的关键。我们应该充分认识到农业科技创新的重要性,加强农业科技研发机构和企业的建设,培养农业科技人才,完善农业科技服务体系,为乡村振兴和农业现代化提供强大的科技支撑。
相关文章:

乡村振兴与农业科技创新:加大农业科技研发投入,推动农业科技创新,促进农业现代化和美丽乡村建设
一、引言 在当代中国,乡村振兴已成为国家发展的重要战略之一。作为国民经济的基础,农业的发展直接关系到国家的稳定和人民的福祉。随着科技的不断进步,农业科技创新在推动农业现代化和美丽乡村建设中发挥着越来越重要的作用。本文旨在探讨如…...

Java 雪花算法:分布式唯一ID生成的魔法秘籍
欢迎来到本次博客的旅程,今天我们要揭开一个神秘算法的面纱,它就是在分布式系统中广受欢迎的——雪花算法(Snowflake)。这个算法不是用来预测雪花的形状,而是用来生成唯一的ID,保证在分布式系统中ÿ…...

mybatis配置环境流程
mybatis配置环境流程 为啥要用mybatis:通过Mybatis实现快速访问后端pgsql、mysql等数据库。 1.修改pom.xml,添加mybatis相关依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-s…...
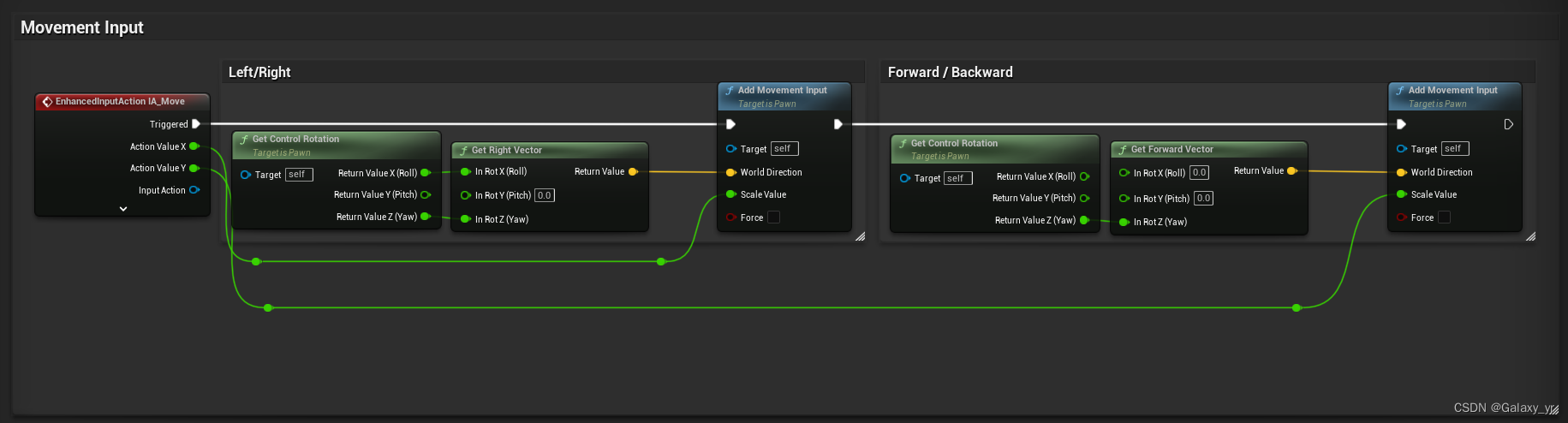
UE5增强输入系统入门
UE4直接在项目设置里设置的轴映射和操作映射在UE5中被标记为废弃,改为使用增强输入系统。 这两天学习了下蓝图和c中增强输入系统的使用,在这里分享一下。 学习使用的模板是第三人称模板(蓝图/c),代码蓝图都参考的模板。 增强输入系统 UE5…...

Python 语法好乱:深度解析与应对策略
Python 语法好乱:深度解析与应对策略 Python,作为一门简洁明了的编程语言,广受编程初学者的喜爱。然而,随着学习的深入,许多学习者会发现Python的语法似乎并不像初看起来那么简单,甚至有时会感到“好乱”。…...

移动端框架:加速移动应用开发与提升跨平台兼容性
在当今快速发展的移动应用领域,开发者们面临着如何快速构建、维护并发布跨平台应用的挑战。为了应对这一挑战,移动端框架应运而生,它们不仅加速了移动应用的开发流程,还提升了应用的跨平台兼容性,并确保了应用性能与原…...

Linux systemctl:掌握软件启动和关闭的利器
Linux systemctl:掌握软件启动和关闭的利器 在 Linux 操作系统中,systemctl 是一个强大的工具,用于管理系统服务的启动、停止和状态监控。本篇博客将深入介绍 systemctl 的使用方法,帮助你更好地掌握软件的启动和关闭。 1. syst…...
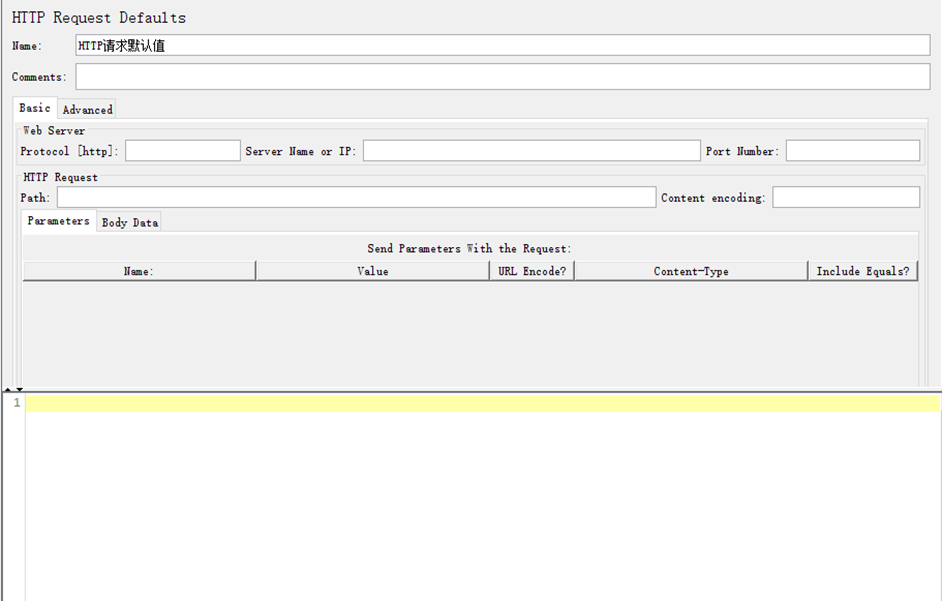
Jmeter干货分享:当你的Log viewer不显示日志时,可能是引入的Jar包冲突导致
问题描述 近期使用Jmeter时发现了一个非常奇怪的问题,就是Jmeter是可以正常使用运行脚本,但是在Log viewer中确没有任何日志,如下图: 问题排查过程 真是百思不得其解啊,在网上各种获取资料,大多数都是说跟…...

网络编程TCP
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🙉 内容推荐:Java网络编程(下)🙉 🐹今日诗词: 壮士当唱大风哥, 宵小之徒能几何?🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微…...

C++中的迭代器
目录 摘要 迭代器类别 1. 输入迭代器(Input Iterator) 2. 输出迭代器(Output Iterator) 3. 前向迭代器(Forward Iterator) 4. 双向迭代器(Bidirectional Iterator) 5. 随机访…...

8.1 Go 包的概念与使用
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
第一篇【传奇开心果系列】AI工业应用经典算法和Python示例:基于AI的智能制造技术经典算法与Python实践
传奇开心果博文系列 系列博文目录AI工业应用经典算法和Python示例系列 博文目录前言一、AI在智能制造方面的应用场景介绍二、基于AI的智能制造技术经典算法介绍三、支持向量机机器学习算法Python示例代码四、随机森林机器学习算法Python示例代码五、深度学习算法Python示例代码…...

Mathtype插入编号的高级格式会重置之前的简单格式的问题
文章标题没说人话,大致意思是: 先以简单格式插入几个编号 再设置高级格式的编号时,即使没有选择插入编号,在点击下图的确定键时,会连带前面的简单公式一并更新 我在网上没有找到相关的问题,即使关闭了…...

弘君资本:存储芯片概念强势,西测测试三连板,佰维存储涨超10%
存储芯片概念3日盘中强势拉升,截至发稿,西测测验、万润科技涨停,佰维存储涨超10%,香农芯创涨近7%,航天智装、普冉股份等涨超5%。值得注意的是,西测测验已连续3个交易日涨停。 职业方面,当时干流…...

【机器学习】逻辑回归:原理、应用与实践
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 逻辑回归:原理、应用与实践引言1. 逻辑回归基础1.1 基本概念1.2 Sig…...

C++:list模拟实现
hello,各位小伙伴,本篇文章跟大家一起学习《C:list模拟实现》,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 ! 如果本篇文章对你有帮助,还请各位点点赞!…...
植物大战僵尸杂交版全平台 PC MAC 安卓手机下载安装详细图文教程
最近植物大战僵尸杂交版非常的火,好多小伙伴都想玩一玩,但作者只分享了 win 版,像手机还有MAC电脑都没有办法安装,身为 MAC 党当然不能放弃,经过一番折腾,也是成功在所有平台包括手机和MAC电脑都成功安装上…...

发送Http请求的两种方式
说明:在项目中,我们有时会需要调用第三方接口,获取调用结果,来实现自己的业务逻辑。调用第三方接口,通常是双方确定好,由对方开放一个接口,需要我们根据他们提供的接口文档,组装Http…...
【算法训练记录——Day23】
Day23——二叉树Ⅸ 669.修剪二叉搜索树108.将有序数组转换为二叉搜索树538.把二叉搜索树转换为累加树 今日内容: ● 669.修剪二叉搜索树 ● 108.将有序数组转换为二叉搜索树 ● 538.把二叉搜索树转换为累加树 ● 总结篇 669.修剪二叉搜索树 思路:主要是…...
【wiki知识库】04.SpringBoot后端实现电子书的增删改查以及前端界面的展示
📝个人主页:哈__ 期待您的关注 目录 一、🔥今日内容 二、🌏前端页面的改造 2.1新增电子书管理页面 2.2新增路由规则 2.3修改the-header代码 三、🚗SpringBoot后端Ebook模块改造 3.1增加电子书增/改接口 3.1.…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
