【数据结构】详解堆的基本结构及其实现
文章目录
- 前言
- 1.堆的相关概念
- 1.1堆的概念
- 1.2堆的分类
- 1.2.1小根堆
- 1.2.2大根堆
- 1.3堆的特点
- 堆的实用场景
- 2.堆的实现
- 2.1初始化
- 2.2插入
- 2.3堆的向上调整
- 2.4删除
- 2.5堆的向下调整
- 2.6判空
- 2.7获取堆顶元素
- 2.8销毁
- 3.堆排序
- 3.1实现
- 3.2堆排序的时间复杂度问题
前言
在上一篇文章中,我们已经了解了树和二叉树的概念,而下面我们要学习的堆,在二叉树中非常重要;
如果的二叉树还不太了解的,大家可以参考作者的上一篇文章
详解二叉树
1.堆的相关概念
1.1堆的概念
现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,
一个是数据结构,一个是操作系统中管理内存的一块区域分段
1.2堆的分类
对于堆我们可以分成两种:
大堆和小堆;
1.2.1小根堆
1.小堆
在小堆中,堆中的某个节点的值总是不小于其父节点的值,换句话说就是父节点的值永远不大于其子节点,而如果有两个子节点时,子节点之间不存在大小限制关系;即指在逻辑上的二叉树结构中,根结点<=子结点,总是最大的,并且在堆的每一个局部都是如此。例如{1,2,3}可以看作为小根堆,而{1,3,2}亦可以看作为小根堆。小根堆的根结点在整个堆中是最小的元素。
1.2.2大根堆
2.大堆
在大堆中,堆中的某个节点的值总是不大于其父节点的值,换句话说就是父节点的值永远不小于其子节点,而如果有两个子节点时,子节点之间不存在大小限制关系;即指在逻辑上的二叉树结构中,根结点>=子结点,总是最大的,并且在堆的每一个局部都是如此。例如{3,1,2}可以看作为大根堆,而{3,2,1}亦可以看作为大根堆。大根堆的根结点在整个堆中是最大的元素。
详情请看下图:
1.3堆的特点
对于二叉树来说,我们用堆来实现,那为什么不用数组来实现呢?
因为对于普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树(也就是堆)更适合使用顺序结构存储。
并且堆还具有以下的特点,让它更加高效和适用:
1.维护有序性:
最大堆:每个节点的值都大于或等于其子节点的值,堆顶元素始终是最大值。
最小堆:每个节点的值都小于或等于其子节点的值,堆顶元素始终是最小值。
这种特性使得堆在需要频繁查找最大或最小元素的场景(如优先队列)中极为高效,无需遍历整个数组即可快速获得。
2.动态调整:
堆支持插入和删除元素的同时能够高效地(通常是O(log n)时间复杂度)重新调整结构以维持其特性,这一点在使用数组时难以直接高效实现。
3.内存利用率:
实际实现时,堆可以采用数组来存储,虽然逻辑上是树状结构,但实际上占用的是连续内存空间,因此内存使用相对高效。
4.排序应用:
堆可以作为实现堆排序的基础,这是一种不稳定的排序算法,其优势在于能够提供较好的最坏情况和平均时间复杂度(O(n log n)),并且不需要像快速排序那样依赖于数据的初始分布。
堆的实用场景
1、我们可以利用堆的性质来找出一个序列中最大/小的元素,尽管通过遍历来解决这一问题可能更好。
2、堆排序,堆排序即利用堆的思想来进行排序,总共分为两个步骤:1.建堆
升序:建大堆
降序:建小堆
2.利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。3、建立优先级队列,根据上述的小结可知,若利用堆来建立优先级队列,可以快速的获取到队列中优先级最高/低的任务。
4、n个元素中排列出前k大的元素问题,对于此类问题,可以建立一个小根堆,依次读入n个元素并调整,并在堆的规模达到k+1时,剔除掉第1个元素,剩下k个较大元素,保持堆的规模不超过k,一直循环即可得到最终的结果。
2.堆的实现
实现堆,首先要知道堆在结构体中的结构是怎样的;
//堆的结构
typedef int HeapTypeData;
typedef struct heap
{HeapTypeData* a;int size;int capacity;
}HP;还有我们要实现的一些接口:
//初始化
void HPInit(HP* php);
//插入
void HPPush(HP* php, HeapTypeData x);
//删除
void HPPop(HP* php);
//判空
bool HPEmpty(HP* php);
//获取堆顶
HeapTypeData HPTop(HP* php);
//销毁
void HPDestory(HP* php);
//向上调整
void AdjustUp(HeapTypeData* a, int n, int parent);
//向下调整
void AdjustDown(HeapTypeData* a, int child);
//交换
void Swap(HeapTypeData* p1, HeapTypeData* p2);
下面我们就来一一实现;
2.1初始化
初始化的过程和顺序表的相似
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}
2.2插入
1.,由于我们是用堆实现的二叉树的顺序结构,在存储结构上还是数组,所以当我们插入时要进行扩容;
2.当我们在尾端插入一个元素时,堆所满足的大根堆或小根堆的条件可能会被违背,所以我们还要再创建一个调整函数AdjustUp将数据进行调整,那么既然要调整,就还需要一个
交换函数swap将数据进行交换
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
2.3堆的向上调整
1.计算父节点位置:首先创建孩子节点下标的索引child(将最后一个叶子节点数据也就是我们插入的数据的下标)计算出其父节点的索引parent,公式为(child - 1) / 2;
2.循环比较并交换:进入一个循环,在循环中不断比较当前孩子节点和其父节点的值。如果孩子节点的值小于父节点的值(对于x小根堆而言),则交换这两个节点的值。这是因为小根堆要求父节点的值不大于子节点的值;
3.更新索引并继续:在交换之后,原来的子节点变成了新的父节点,因此需要更新child为parent,同时基于新的child计算新的parent,继续进行比较和可能的交换,直到孩子节点不再小于其父节点或者到达了堆的根部(即child <= 0时);
4.退出循环:一旦发现孩子节点不小于其父节点,或者已经没有父节点可比较(即到达了树的根),循环结束,此时堆的性质已经得到恢复;
注意:1.这里我们创建的child,parent,所指向的都是节点的下标
2.这里我们使用小根堆来进行示范,当调整大根堆时只需要将循环中if语句的判断符号改为大于号就可以了;
void AdjustUp(HPDataType* a, int child)
{// 初始条件// 中间过程// 结束条件int parent = (child - 1) / 2;//while (parent >= 0)错误while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
2.4删除
删除我们也要考虑堆的性质问题——是否成立
所以这里也需要判断,并进行调整,而删除时由于删除的时堆顶的数据,所以我们要有一个向下调整的函数来调整整个堆;那么我们删除的逻辑就是:
1.将堆顶的元素和堆尾的元素进行交换,这样删除时更加简单,只需要将size–就可以了;
2.我们再把交换到堆顶的元素,进行调整,使之满足堆的成立条件;这里我们还是用小根堆进行示范;
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size-1]);php->size--;AdjustDown(php->a, php->size, 0);
}2.5堆的向下调整
1.初始化子节点位置:首先创建出计算出当前父节点的左孩子的索引child,公式为parent * 2 + 1。
2.循环比较并交换:进入循环,只要child的值小于n,表示还有子节点可以比较。… 1.选择较小的子节点:如果右孩子存在(即child + 1 < n)且右孩子的值小于左孩子的值,则将child更新为右孩子的索引,因为我们要找到两个子节点中更小的那个。
… 2.比较并交换:如果找到的子节点child的值小于其父节点parent的值,说明违反了最小堆的性质,这时需要交换它们的值,并将当前的child位置作为新的父节点位置继续向下比较。
… 3.更新位置:交换后,原child位置已成为新的父节点位置,因此更新parent = child,并基于新的父节点重新计算其左孩子的索引child = parent * 2 + 1,继续循环。
… 4.退出条件:如果子节点不小于父节点,或者已经没有更多的子节点可比较(即child >= n),则跳出循环。3.结束:循环结束后,堆的性质得到了恢复,即以parent为根的子树满足最小堆的定义。
void AdjustDown(HPDataType* a, int n, int parent)
{// 先假设左孩子小int child = parent * 2 + 1;while (child < n) // child >= n说明孩子不存在,调整到叶子了{// 找出小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}2.6判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}
2.7获取堆顶元素
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}
2.8销毁
销毁时要注意一一销毁,并且把变量置为零;
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
3.堆排序
3.1实现
堆排序首先要建堆,建堆时:
1.升序,建大堆;
2.降序,建小堆;
而对于这两种建堆方式,我们选择用第二种,因为我们从时间复杂度的角度去对比时会发现:
1.建大堆的时间复杂度为O(N*logN);
2.建小堆的则为O(N);
所以我们选择第二种;
1.建堆:
我们从最后一个非叶节点开始逆序遍历至根节点的方式来构建最小堆。这样做的目的是直接通过向上调整函数递归调整每个子树为最小堆,最终整个数组构成一个最小堆。计算最后一个非叶节点的索引公式为(sz-1-1)/2,然后从这个索引开始,逐步向前执行向上调整操作。
(sz-1-1)/2:sz-1->最后一个元素,(sz-1-1)/2找到父节点
2.排序:
首先,将堆顶元素(数组中的最小值)与数组末尾元素交换,确保当前最小值位于正确的位置(即数组末尾)。
然后,因为堆顶元素(现在是数组的末尾元素)已经正确排序,所以缩小堆的有效大小(end -= 1),并在剩下的元素中再次调用向上调整函数调整剩余元素为最小堆。这个过程重复,直到整个数组都被正确排序。
void HeapSort(int* a, int n)
{// 降序,建小堆// 升序,建大堆// 向上调整建堆 O(N*logN)/*for (int i = 1; i < n; i++){AdjustUp(a, i);}*/// 向下调整建堆 O(N)for (int i = (n-1-1)/2; i >= 0; i--){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
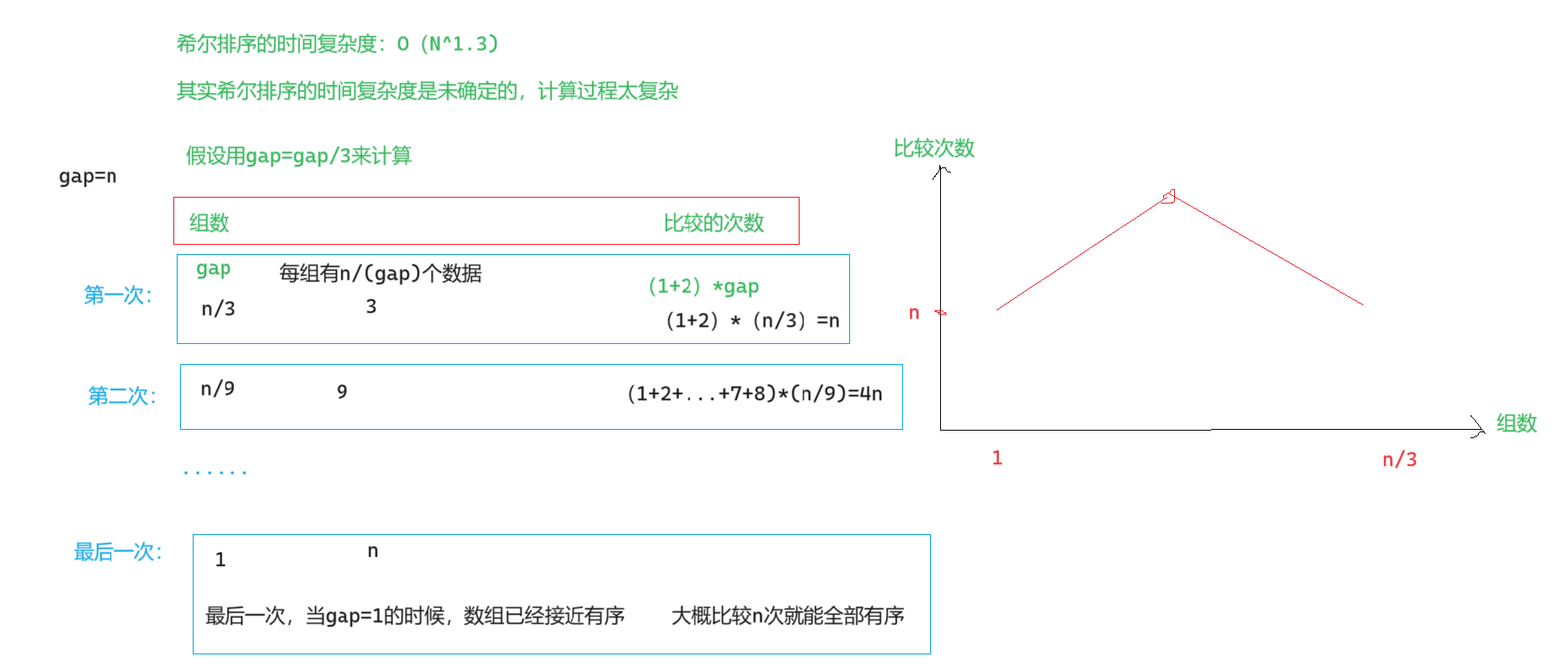
}3.2堆排序的时间复杂度问题
我们通过两张图来理解:
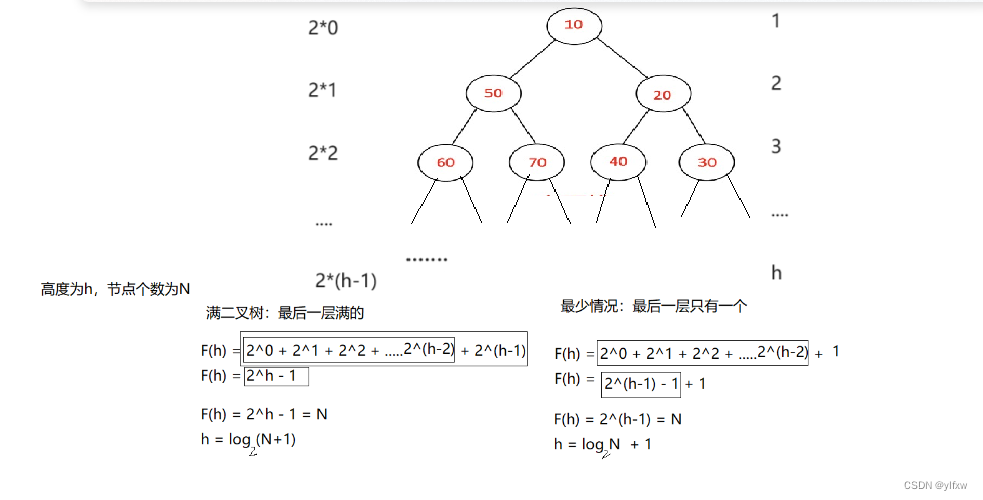
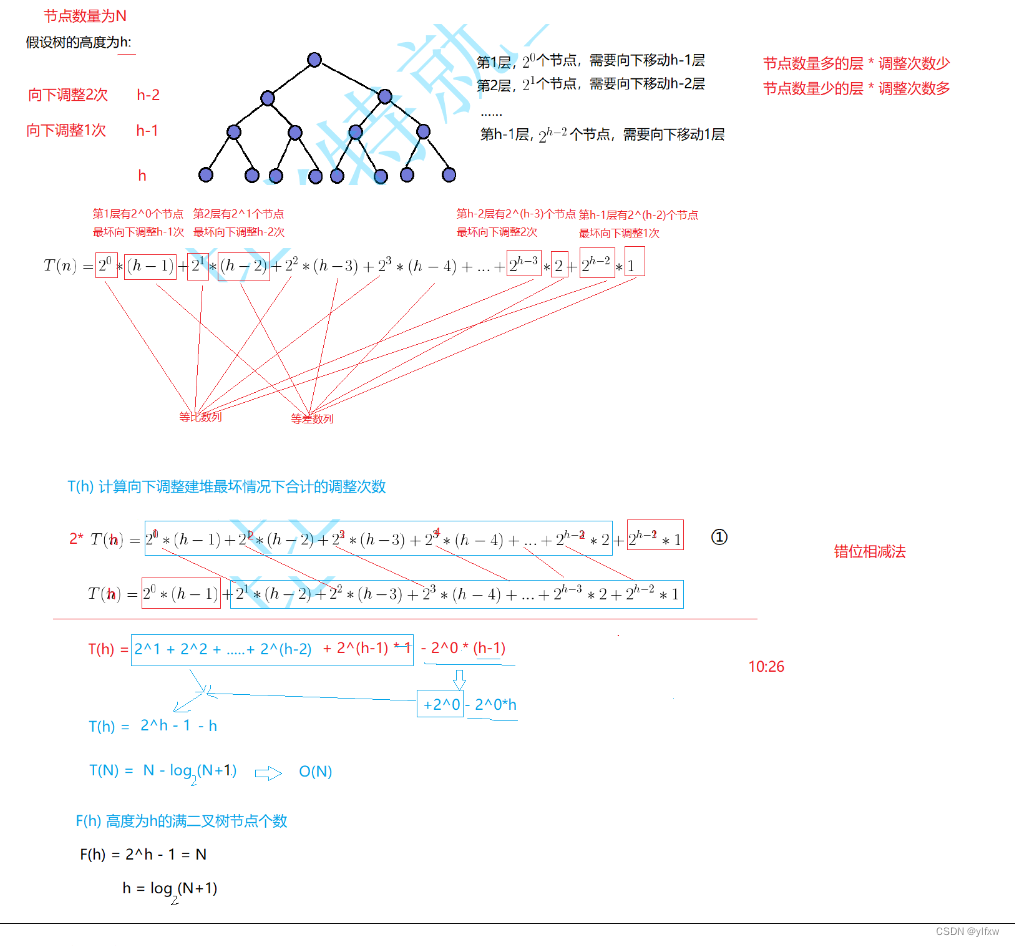
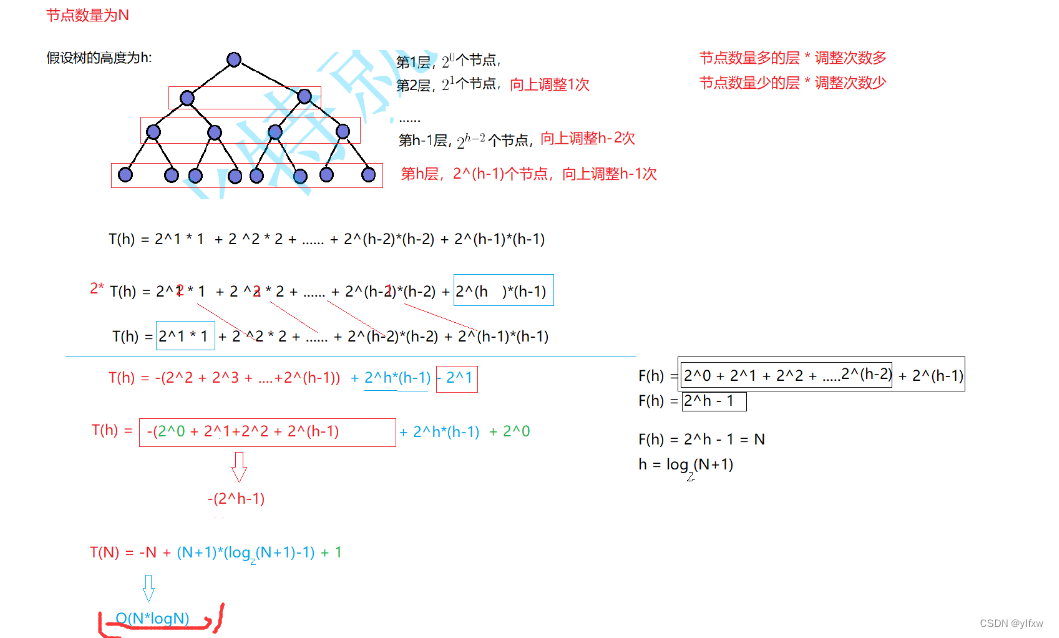
最后得出结果为O(N*logN);
相关文章:

【数据结构】详解堆的基本结构及其实现
文章目录 前言1.堆的相关概念1.1堆的概念1.2堆的分类1.2.1小根堆1.2.2大根堆 1.3堆的特点堆的实用场景 2.堆的实现2.1初始化2.2插入2.3堆的向上调整2.4删除2.5堆的向下调整2.6判空2.7获取堆顶元素2.8销毁 3.堆排序3.1实现3.2堆排序的时间复杂度问题 前言 在上一篇文章中&#…...
python无限弹窗的代码
一个简单的Python代码示例,用于在特定的时间间隔内显示一个简单的弹窗。这个代码使用了Python的tkinter库来创建一个简单的GUI窗口。 python import tkinter as tk import time def popup(): popup_window.deiconify() # 显示窗口 popup_window.wait_window() # 等…...

多线程新手村5--线程池
1.1 线程池是什么 线程诞生的意义是因为进程的创建/销毁开销太大,所以使用线程提高代码的执行效率;那如果想要进一步提升执行效率,该怎么办呢?有一个方法是使用线程池。 首先,什么是线程池:池就是池子&am…...
数据库 mysql 的彻底卸载
MySQL卸载步骤如下: (1)按 winr 快捷键,在弹出的窗口输入 services.msc,打开服务列表。 (2)在服务列表中, 找到 mysql 开头的所有服务, 右键停止,终止对应的…...

Meterpreter工具使用
Meterpreter属于stage payload,在Metasploit Framework中,Meterpreter是一种后渗透工具,它 属于一种在运行过程中可通过网络进行功能扩展的动态可扩展型Payload。这种工具是基于“内存DLL注 入”理念实现的,它能够通过创建一个新进…...

第四讲 单片机STC89C52+RA8889代码移植范例(包含API接口)
本次介绍单片机STC89C52RA8889代码移植范例,该范例已将RA8889的API移植好了,下方提供下载地址。 硬件平台:89C52RA8889 采用SPI通信方式 (已测试通过) 上一讲已经阐述RA8889移植到51单片机的基本方法,本讲增加了API…...

QT 音乐播放器【一】 显示音频级别指示器
文章目录 效果图概述代码总结 效果图 概述 QMediaPlayer就不介绍了,就提供了一个用于播放音频和视频的媒体播放器 QAudioProbe 它提供了一个探针,用于监控音频流。当音频流被捕获或播放时,QAudioProbe 可以接收到音频数据。这个类在需要访问…...
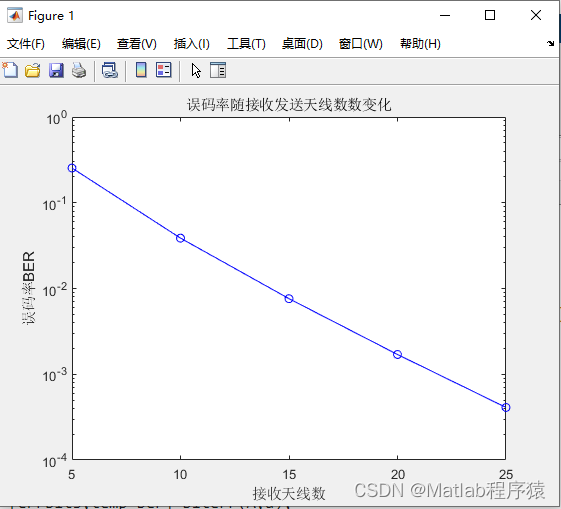
【MATLAB源码-第220期】基于matlab的Massive-MIMO误码率随着接收天线变化仿真采用ZF均衡和QPSK调制。
操作环境: MATLAB 2022a 1、算法描述 1. 系统背景与目标 无线通信系统的发展极大地推动了现代通信技术的进步,从移动通信到无线局域网,甚至是物联网,均依赖于无线通信系统的高效和可靠性。在无线通信系统中,核心目…...
【前端】政务服务大数据可视化监控平台(源码+html+css+js)
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉公众号👈:测试开发自动化【获取源码商业合作】 👉荣__誉👈:阿里云博客专家博主、5…...

【网关】工业智能网关-02
一 公司简介 保定飞凌嵌入式技术有限公司始于2006年,是一家专注嵌入式核心控制系统研发、设计和生产的高新技术企业,是国内最早专业从事嵌入式技术的企业之一。 经过十几年的发展与积累,公司拥有业内一流的软硬件研发团队,在北京…...

【C语言】动态内存管理技术文档
【C语言】动态内存管理技术文档 目录 【C语言】动态内存管理技术文档 一、内存管理基础...

低空经济的意义所在
发展低空经济对于推动经济发展、促进产业升级、降低运输成本、构建综合交通系统等方面都具有重要意义。低空经济对推动经济发展提供新动能。低空经济作为新兴产业,具有巨大的发展潜力,能够带动投资、促进消费,为经济增长注入新动力。除此之外…...
DNF手游攻略:0氪攻略,转职技巧与避坑指南!
在DNF手游的冒险旅程中,角色的转职是一次重要的成长经历。通过转职,玩家可以获得全新的技能和属性,提升自己在地下城中的战斗力。本文将为您介绍转职后的关键技巧和日常任务,帮助您更好地适应新的职业身份,成为地下城中…...

周报 | 24.5.27-24.6.2文章汇总
为了更好地整理文章和发表接下来的文章,以后每周都汇总一份周报。 周报 | 24.5.20-24.5.26文章汇总-CSDN博客 集智书童 | YOLOv10开源|清华用端到端YOLOv10在速度精度上都生吃YOLOv8和YOLOv9_yolov8 yolov10-CSDN博客 机器之心 | 清华接手,…...
【C++初阶学习】第十二弹——stack和queue的介绍和使用
C语言栈:数据结构——栈(C语言版)-CSDN博客 C语言队列:数据结构——队列(C语言版)-CSDN博客 前言: 在之前学习C语言的时候,我们已经学习过栈与队列,并学习过如何使用C语言来实现栈与队列&…...

nginx反向代理了解
文章目录 Nginx反向代理反向代理系统调优Proxy Buffer相关指令 Nginx 具有高性能的http和反向代理的web服务器,同时也是一个pop3/smtp/imap代理服务器,使用c语言编写 **Web服务器:**也叫网页服务器,web server,主要功…...
插入排序和希尔排序
目录 1.直接插入排序2.希尔排序 1.直接插入排序 基本思想: 把待排序的数据按其大小逐个插入到一个已经排好序的有序序列中,直到所有的数据插入完成为止。 当插入第i个元素时,前面的a[0],a[1],...,a[i-1]个数据已经排好序了,此时用…...
Java web应用性能分析之【java进程问题分析定位】
Java web应用性能分析之【java进程问题分析概叙】-CSDN博客 Java web应用性能分析之【java进程问题分析工具】-CSDN博客 Java web应用性能分析之【jvisualvm远程连接云服务器】-CSDN博客 由于篇幅限制、前面三篇讲了准备工作和分析小结,这里将详细操作java进程问题…...

c#控件笔记
c# PictureBox在工具箱的哪个位置 在 Visual Studio 的工具箱中,PictureBox 控件位于 “Common Controls” 部分。要找到 PictureBox,请按照以下步骤操作: 打开 Visual Studio 并加载您的项目。确保已经打开了设计器视图(即您的…...
STM32-15-DMA
STM32-01-认识单片机 STM32-02-基础知识 STM32-03-HAL库 STM32-04-时钟树 STM32-05-SYSTEM文件夹 STM32-06-GPIO STM32-07-外部中断 STM32-08-串口 STM32-09-IWDG和WWDG STM32-10-定时器 STM32-11-电容触摸按键 STM32-12-OLED模块 STM32-13-MPU STM32-14-FSMC_LCD 文章目录 STM…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

