鲁教版七年级数学下册-笔记
文章目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- 5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行限的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式与一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
第七章 二元一次方程组
1 二元一次方程组
- 含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程
- 像这样共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组
- 适合一个二元一次方程的未知数的值,叫做这个二元一次方程的一个解
- 二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解
2 解二元一次方程组
- 解方程组的基本思路就是“消元”—把“二元”变为“一元”,这种解方程组的方法称为代入消元法,简称代入法
- 通过两式相加减消去其中一个未知数,这种解方程组的方法称为加减消元法,简称加减法
3 二元一次方程组的应用
4 二元一次方程与一次函数
5 三元一次方程组
- 含有三个未知数,并且所含未知数的项的次数都是1的方程叫做三元一次方程
- 像这样共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组
- 三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解
- 解三元一次方程组的思路仍然是“消元”—把三元化为二元,在化为一元。
第八章 平行线的有关证明
1 定义与命题
- 判断一件事情的句子,叫做命题
- 命题通常由条件和结论两部分组成
- 正确的命题叫做真命题
- 不正确的命题叫做假命题
2 证明的必要性
- 要判断一个命题是不是真命题,仅仅依靠经验、观察、实验和猜想是不够的,必须一步步、有根有据地进行推理。推理的过程就是证明
3 基本事实与定理
- 经过长期实践总结出来,并且被人们公认的真命题叫做公理
- 除了公理外,其他真命题的正确性都通过推理的方法证实。经过证明的真命题叫做定理
4 平行线的判定定理
- 定理 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
- 同旁内角互补,两直线平行
- 内错角相等,两直线平行
5 平行限的性质定理
- 两直线平行,同位角相等
- 两直线平行,内错角相等
- 两直线平行,同旁内角互补
6 三角形内角和定理
- 三角形内角和等于180°
- 直角三角形的两个锐角互余
- 三角形的一个外角等于和它不相邻的两个内角的和
- 三角形的一个外角大于任何一个和它不相邻的内角
第九章 概率初步
1 感受可能性
- 在一定条件下,有些事件一定发生,这些事件称为必然性事件
- 在一定条件下,有些事件一定不会发生,这些事件称为不可能事件
- 必然事件与不可能事件统称为确定事件
2 频率的稳定性
- 必然事件发生的概率为1;不可能事件发生的概率为0;不确定事件A发生的概率P(A)是0与1之间的一个常数
3 等可能事件的概率
第十章 三角形的有关证明
1 全等三角形
- 基本事实: 两边及其夹角相等的两个三角形全等。(SAS)
- 基本事实: 两角及其夹边相等的两个三角形全等。(ASA)
- 基本事实: 三条边相等的两个三角形全等。(SSS)
- 两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS)
2 等腰三角形
- 等腰三角形的两个底角相等
- 等腰三角形顶角的平分线、底边的中线,底边上的高互相重合。
- 有两个角相等的三角形是等腰三角形
- 有一个角是60° 的等腰三角形是等边三角形
- 在直角三角形中,如果一个锐角等于30° ,那么它所对的直角边等于斜边的一半
3 直角三角形
- 勾股定理 直角三角形两条直角边的平方和等于斜边的平方
- 如果三角形两边的平法和等于第三边的平方,那么这个三角形一定是直角三角形
- 斜边和一条直角边分别相等的两个直角三角形全等
4 线段的垂直平分线
- 线段垂直平分线上的点到这条线段两个端点的距离相等。
- 到线段两个端点距离相等的点在这条线段的垂直平分线上。
5 角平分线
- 角平分线上的点到这个角的两边的距离相等
- 在一个角的内部,并且到角的两边距离相等的点,在这个角的角平分线上
第十一章 一元一次不等式与一元一次不等式组
1 不等关系
2 不等式的基本性质
- 不等式的基本性质1 不等式的两边都加(减)同一个整式,不等号的方向不变
- 不等式的基本性质2 不等式的两边都乘(除以)同一个正数,不等号的方向不变
- 不等式的基本性质3 不等式的两边都乘(除以)同一个负数,不等号的方向改变
3 不等式的解集
- 能使不等式成立的未知数的值,叫做不等式的解
- 一个含有未知数的不等式的所有解,组成这个不等式的解集
4 一元一次不等式
- 这些不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式
5 一元一次不等式与一次函数
6 一元一次不等式组
- 关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组
相关文章:

鲁教版七年级数学下册-笔记
文章目录 第七章 二元一次方程组1 二元一次方程组2 解二元一次方程组3 二元一次方程组的应用4 二元一次方程与一次函数5 三元一次方程组 第八章 平行线的有关证明1 定义与命题2 证明的必要性3 基本事实与定理4 平行线的判定定理5 平行限的性质定理6 三角形内角和定理 第九章 概…...

带你走进在线直线度测量仪 解析测量方法!
在线直线度测量仪 在线直线度测量仪可安装于生产线上,进行非接触式的无损检测,能检测米直线度尺寸,对截面为圆形的产品,进性直线度检测的帮手。 测量方法 在线直线度拟采用我公司的光电测头对矫直后的棒材直线度进行测量。测量时…...

力扣1 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...
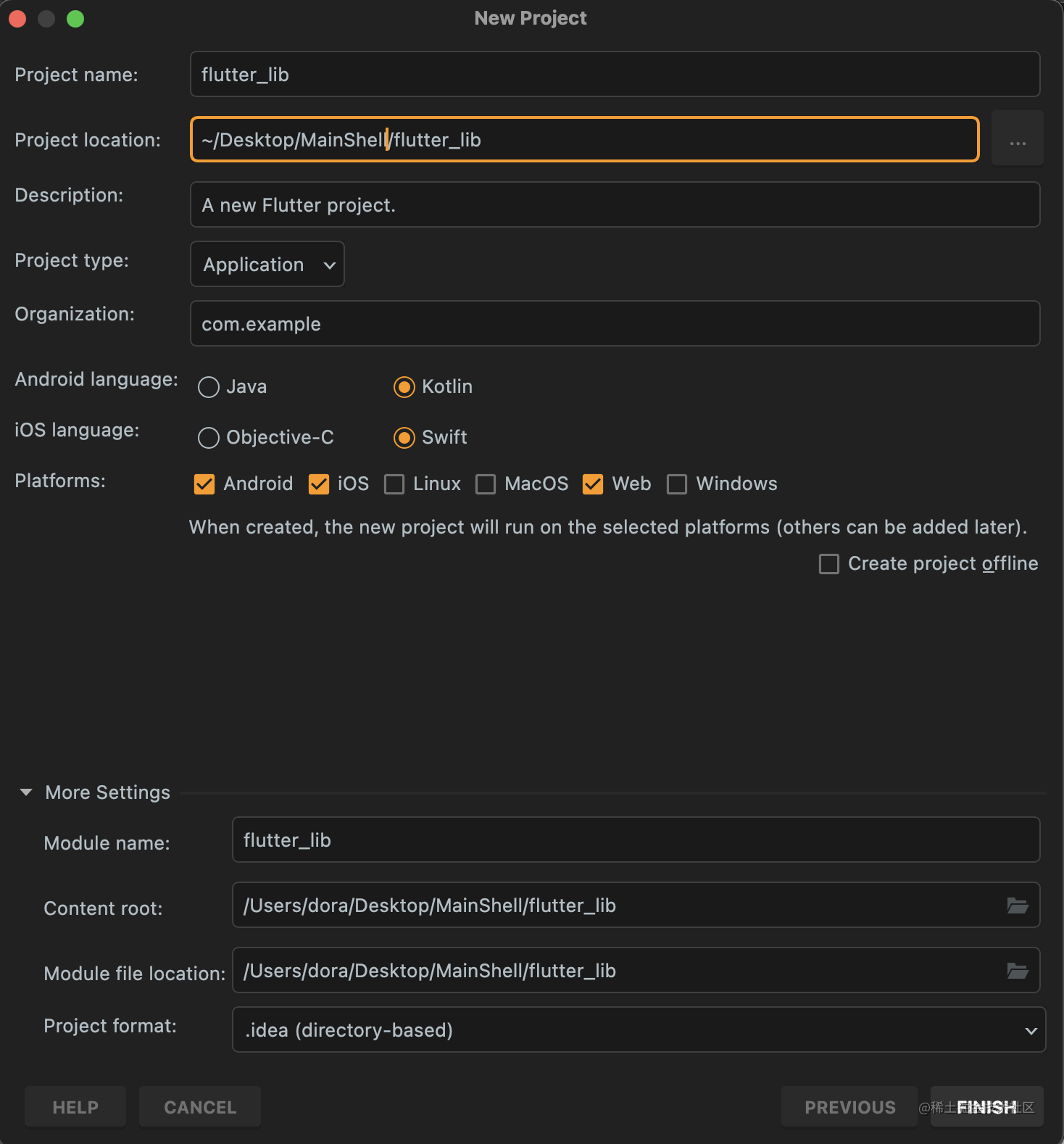
AndroidFlutter混合开发
为什么要有混合开发 我们知道,Flutter是可以做跨平台开发的,即一份Flutter的Dart代码,可以编译到多个平台上运行。这么做的好处就是,在不降低多少性能的情况下,尽最大可能的节省开发的时间成本,直接将开发…...
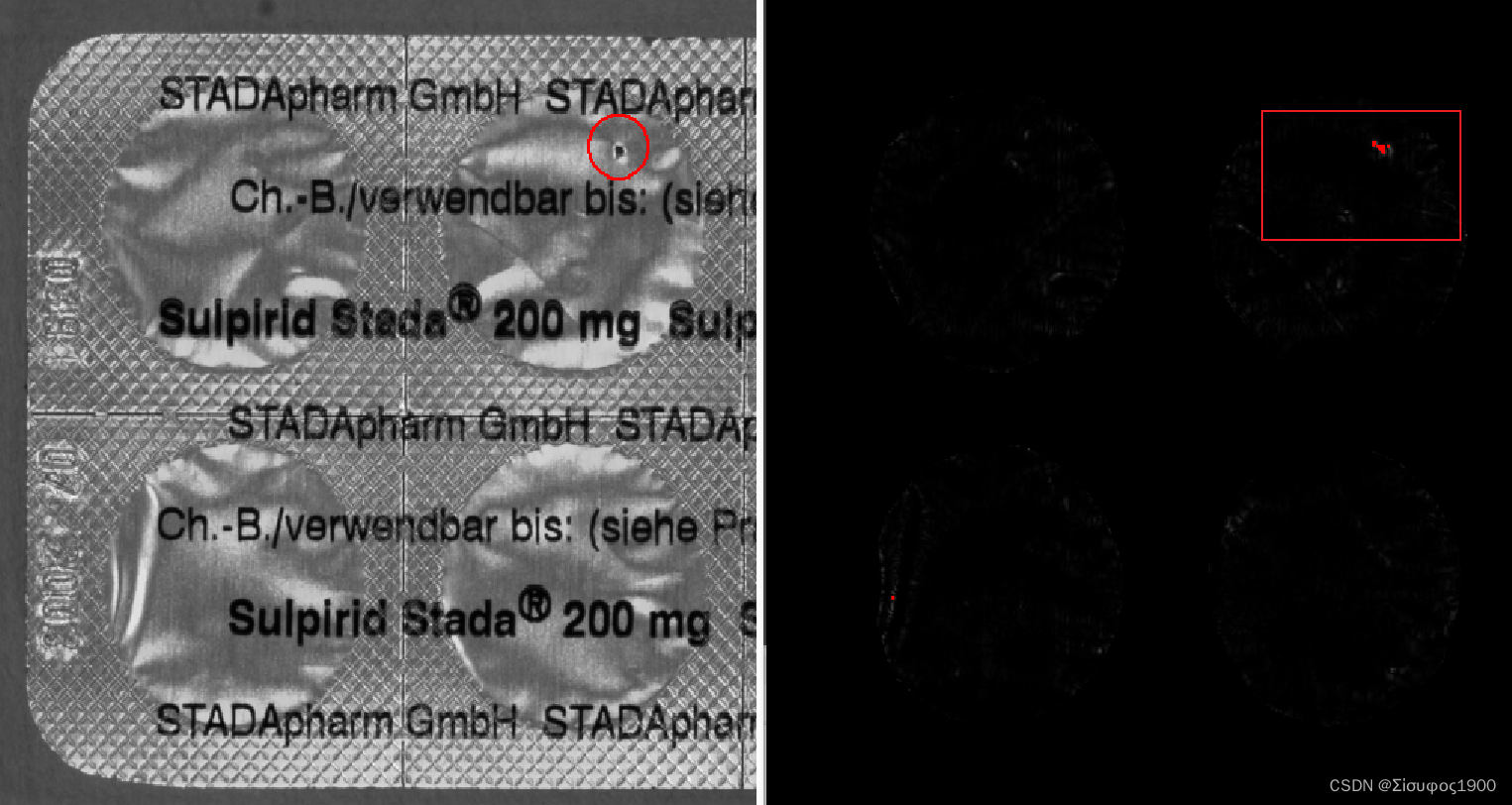
Halcon 光度立体 缺陷检测
一、概述 halcon——缺陷检测常用方法总结(光度立体) - 唯有自己强大 - 博客园 (cnblogs.com) 上周去了康耐视的新品发布会,我真的感觉压力山大,因为VM可以实现现在项目中的80% 的功能,感觉自己的不久就要失业了。同时…...

关于找暑期实习后的一些反思
日期 2024年6月3日 写在前面:距离研究生毕业还有9个月,前端时间一直在不停地投简历,不停地刷笔试题,不停地被拒绝,今天悬着的心终于死透了,心情还是比较糟糕的,可能唯一的安慰就是一篇小论文终于…...

Rust struct
Rust struct 1.实例化需要初始化全部成员变量2.如果需要实例化对象可变,加上mut则所有成员变量均可变 Rust支持通过已实例化的对象,赋值给未赋值的对象的成员变量 #![allow(warnings)] use std::io; use std::error::Error; use std::boxed::Box; use s…...
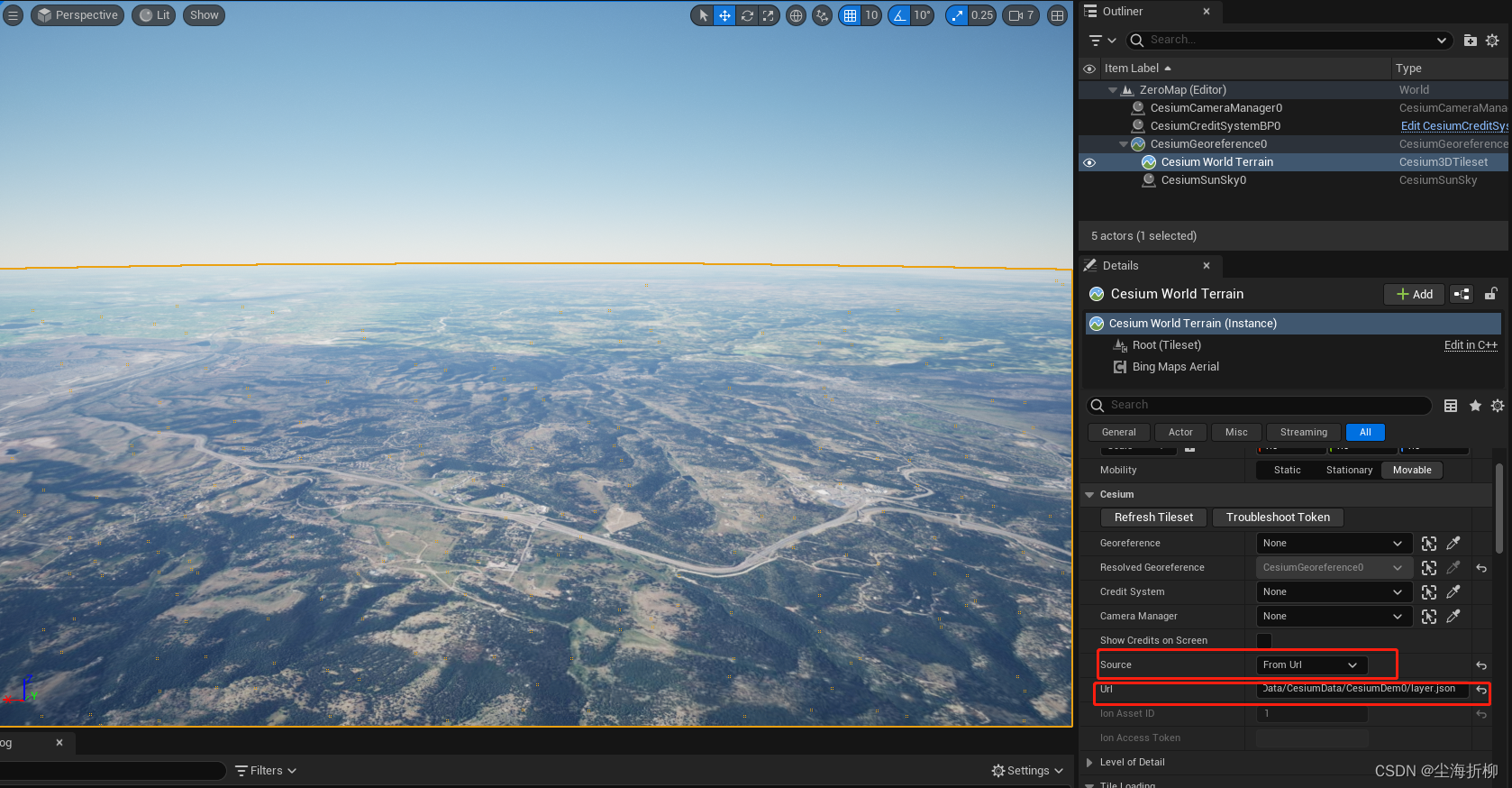
【UE5:CesiumForUnreal】——加载无高度地形数据
目录 1.实现目的 2.数据准备 2.1下载数据 2.2 数据切片 3.加载无地形数据 1.实现目的 在CesiumForUnreal插件中,我们加载地图和地形图层之后,默认都是加载的带有高程信息的地形数据,在实际的项目和开发中,有时候我们需要加载无…...
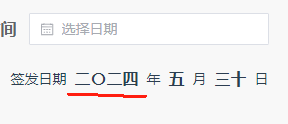
证件/文书类日期中文大写js/ts插件
说明 证件/文书类落款日期中文大写往往会将“零”写作“〇”,而数字依然使用简体“一二三”,而不是“壹贰叁”。 如下: 针对这一点,写了如下转换插件。 代码 function DateToUpperCase(date: Date new Date()) {const chStr …...
))
03JAVA基础(方法/类/封装(构造方法))
目录 1.方法 1.1 方法的定义 1.2 方法的重载 2.类和对象 3.封装 1. private关键字 2. this关键字 3. 封装 4. 构造方法 1.方法 含义: 将具有独立功能的代码块组织成一个整体,具有特殊功能的代码集 注意: 方法必须先创建才可以使用,需要手动调用执行 1.1 方法的定义 格…...

数据容器的通用操作、字符串大小比较 总结完毕!
1.数据容器的通用操作 1)五类数据容器是否都支持while循环/for循环 五类数据容器都支持for循环遍历 列表、元组、字符串都支持while循环,集合、字典不支持(无法下标索引) 尽管遍历的形式不同,但都支持遍历操作 2&a…...
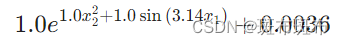
KAN(Kolmogorov-Arnold Network)的理解 3
系列文章目录 第一部分 KAN的理解——数学背景 第二部分 KAN的理解——网络结构 第三部分 KAN的实践——第一个例程 文章目录 系列文章目录前言KAN 的第一个例程 get started 前言 这里记录我对于KAN的探索过程,每次会尝试理解解释一部分问题。欢迎大家和我一起讨…...
lux和ffmpeg进行下载各大主流自媒体平台视频
1、lux下载,链接:https://pan.baidu.com/s/1WjGbouL3KFTU6LeqZmACpA?pwdagpp 提取码:agpp 2、ffmpeg下载,跟lux放在同一个目录; 3、为lux、ffmpeg设置环境变量; 4、WINR,打开运行࿰…...

day25-XML
1.xml 1.1概述【理解】 1.2语法规则【应用】 1.5DTD约束【理解】 1.6schema约束【理解】 1.4xml解析【应用】 概述 xml解析就是从xml中获取到数据 常见的解析思想 DOM(Document Object Model)文档对象模型:就是把文档的各个组成部分看做成对应的对象。 会把xml文件全部加载到…...
Mixly 开启WIFI AP UDP收发数据
一、开发环境 软件:Mixly 2.0在线版 硬件:ESP32-C3(立创实战派) 固件:ESP32C3 Generic(UART) 测试工工具:NetAssist V5.0.1 二、实现功能 ESP32开启WIFI AP,打印接入点IP地址,允许…...

OCR图片转Excel表格:没结构化的弊端
随着OCR技术的不断发展,将表格图片转为excel已不再是难题,但是,目前市面上的程序还大多处于仅能将图片表格转为普通的excel格式阶段,而不能将其结构化,这样就会产生许多的弊端,具体弊端如下: &l…...
查看所用数据库的版本
通过查询 SELECT VERSION();...
U盘感染病毒,不必急于扔掉!教你如何有效清除U盘中的病毒
U盘被感染了只能扔掉吗?随着信息时代的飞速发展,U盘已成为我们日常生活中不可或缺的存储设备。然而,在使用U盘的过程中,我们有时会遇到U盘被病毒感染的情况。面对这一问题,许多人可能会感到恐慌,甚至想要直…...

新手小白也能玩转跨境电商:从零到精通的操作流程
随着全球化的浪潮愈演愈烈,跨境电商已成为众多创业者和企业家的瞩目焦点。然而,对于初涉此领域的新手来说,从零开始构建跨境电商业务可能会面临诸多挑战。本文将为您梳理跨境电商运营的基本操作流程,并指引新手小白如何迈出坚实的…...

川北医学院与爱尔眼科医院集团签署战略合作协议共谋医学发展新篇章
为深入贯彻落实党的二十大精神,统筹校、企、医、政多方资源,服务“健康中国”战略,推动眼健康产业发展,打造国家及区域级眼科医学中心,2024年5月31日,川北医学院与爱尔眼科医院集团在成都举行战略合作协议签…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
