React 为什么使用map来渲染列表 而不是其他循环方法
1. 声明式与函数式编程
React强调声明式编程,这意味着你只需要关心代码“做什么”,而不是“怎么做”。.map()函数是一种高阶函数,它属于函数式编程范畴,能够返回一个新数组,这非常适合用于生成组件列表。
使用.map()可以直接从数据数组转换到JSX数组,使得代码更简洁、更易于理解。例如:
const numbers = [1, 2, 3, 4, 5];
const listItems = numbers.map((number) =><li key={number.toString()}>{number}</li>
);
2. 返回值
.map()函数的另一个优点是它返回一个新的数组,每个数组元素都是回调函数的结果。这与React的更新和渲染模式非常契合,因为React期望你能构建并返回一个完整的元素树,然后由React来处理实际的DOM更新。
return (<ul>{listItems}</ul>
);
3. 简洁性和组合性
与传统的for循环或forEach相比,.map()通常可以用更少的代码完成同样的工作,并且更加直观。for循环或forEach可能需要额外的步骤来构建数组,而.map()自然而然地处理并返回新的数组元素。
4. 组件关键字key的直接支持
当使用.map()来渲染列表时,很容易在同一个表达式中插入key属性,这对于React来说是必需的,以便它可以有效地比较和重新渲染列表。如:
const todos = [{ id: 1, text: 'Learn React' }, { id: 2, text: 'Write Code' }];
const todoList = todos.map((todo) =><li key={todo.id}>{todo.text}</li>
);
在这里,每个<li>元素都有一个唯一的key,这是直接从数据对象中取得的。
5. 性能优化
因为.map()是纯函数,它不会改变原始数组,而是返回一个新数组。这对于避免副作用和在React应用中进行性能优化非常重要,因为React可以轻松跟踪那些未被修改的数据和组件,从而避免不必要的重新渲染。
总结
总之,.map()在React中被推荐用于渲染列表主要是因为它符合React的声明式和函数式编程范式,能够高效地从数据生成组件,并且代码更加简洁、易于维护。当然,在某些特定情况下,可能会需要使用for循环或其他方法,但这些情况比较少见。
相关文章:

React 为什么使用map来渲染列表 而不是其他循环方法
1. 声明式与函数式编程 React强调声明式编程,这意味着你只需要关心代码“做什么”,而不是“怎么做”。.map()函数是一种高阶函数,它属于函数式编程范畴,能够返回一个新数组,这非常适合用于生成组件列表。 使用.map()…...
【Axure高保真】tab切换输入表单
今天和大家分享tab切换输入表单的原型模板,这个模板方便我们快速制作表单,里面包含了输入框、下拉列表、选择器共10多种常用的元件,后续也可以根据需要自行添加到中继器里。点击tab标签可以分类填写对应的内容,这个原型模板是用中…...

OrangePi AI Pro 测试体验
感谢CSDN活动提供的OrangePi AI Pro ,之前一直用的树莓派,正好体验一下新的国产设备, 1、开机体验 整个设备包装不错,链接键盘、屏幕和鼠标,整体开机体验不错,内置OS不错,这个系统内嵌了中文输…...
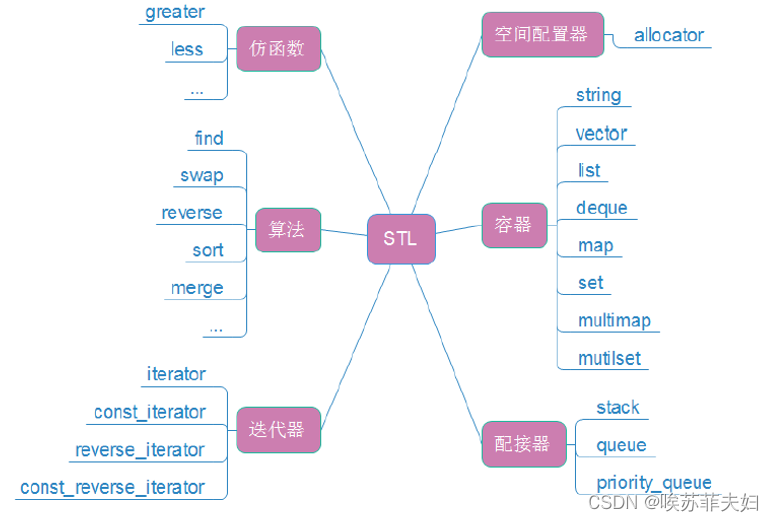
【C++】:模板初阶和STL简介
目录 一,泛型编程二,函数模板2.1 函数模板概念2.2 函数模板格式2.3 函数模板的原理2.4 函数模板的实例化2.5 模板参数的匹配原则 三,类模板3.1 类模板的定义格式3.2 类模板的实例化 四,STL简介(了解)4.1 什…...

【软件开发】Java学习路线
本路径视频教程均来自尚硅谷B站视频,Java学习课程我已经收藏在一个文件夹下,B站文件夹同时会收藏其他Java视频,感谢关注。指路:https://www.bilibili.com/medialist/detail/ml3113981545 2024Java学习路线(快速版&…...

git拉去代码报错“Failed to connect to 127.0.0.1 port 31181: Connection refused“
最近参与了一个新项目,在使用git clone 克隆代码时遇到了一个报错"fatal: unable to access ‘https://example.git/’: Failed to connect to 127.0.0.1 port 31181: Connection refused",今天就和大家分享下解决过程。 报错详情 在使用git clone 克隆…...

解读信创产业根基,操作系统发展历程
信创产业根基之一操作系统 操作系统是一个关键的控制程序,负责协调、管理和控制计算机硬件和软件资源。作为硬件的首要软件扩展,它位于裸机与用户之间,充当了两者之间的桥梁。通过其核心程序,操作系统高效地管理着系统中的各类资源…...

使用Python爬取华为市场游戏类APP应用
文章目录 1. 写在前面2. 接口分析3. 爬虫开发4. 下载链接获取 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守…...

【Oracle】修改已经存在的序列的当前值
前情提要 在oracle中一般使用序列来实现ID自增。但是oracle中序列维护的没有mysql那么好。只是单存的递增。 比如新建了一个序列,从1开始,每次递增1。此时我向数据库里插入一条id10的数据。那么在序列查询到10的时候,插入就会报错。 所以比较…...
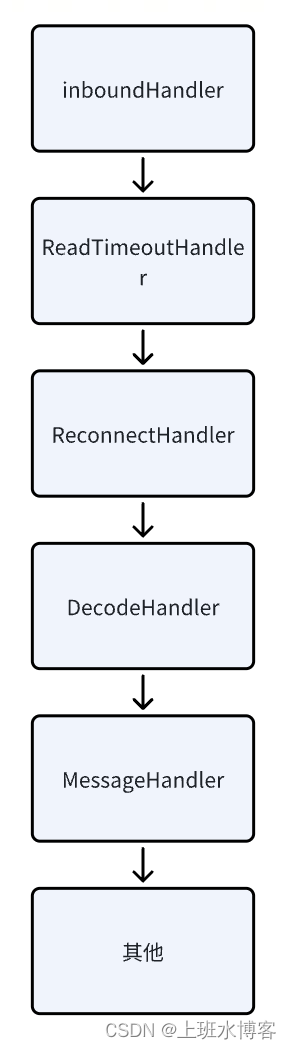
记一次netty客户端的开发
背景 近日要开发一个tcp客户端程序去对接上游厂商的数据源,决定使用netty去处理,由于很久没有开发过netty了,顺便学习记录下 netty搭建 考虑到我们需要多个client去对接server服务,所以我们定义一个公共的AbstractNettyClient父…...

策略模式结合Spring使用
1.抽象策略 /*** 支付方式策略* author Linging* version 1.0.0* since 1.0*/ public interface PayStrategy {void pay(BigDecimal money);}2.具体策略 /*** 支付宝* author Linging* version 1.0.0* since 1.0*/ Component("aliPayStrategy") public class AliPa…...

基于 RNNs 对 IMDB 电影评论进行情感分类
前言 系列专栏:【深度学习:算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域,讨论了各种复杂的深度神经网络思想,如卷积神经网络、循环神经网络、生成对抗网络、门控循环单元、长短期记…...

Midjourney绘画参数设置详解
在数字艺术和设计领域,Midjourney是一款强大的绘画工具,它允许艺术家和设计师以数字方式创作出精美的图像。为了充分发挥Midjourney的潜力,正确设置其绘画参数至关重要。本文将深入探讨Midjourney的绘画参数设置,帮助用户更好地掌…...

计算机毕业设计 | springboot养老院管理系统 老人社区管理(附源码)
1,绪论 1.1 背景调研 养老院是集医疗、护理、康复、膳食、社工等服务服务于一体的综合行养老院,经过我们前期的调查,院方大部分工作采用手工操作方式,会带来工作效率过低,运营成本过大的问题。 院方可用合理的较少投入取得更好…...

事务与并发控制
事务(Transaction0):要么全做,要么全不做; 事务ACID:原子性Atomicity;一致性Consistency;隔离性Isolation;持久性Durability; 并发操作问题: 1.…...

spring boot 中的异步@Async
spring boot 开启异步调用 1、启动类上添加EnableAsync注解,表示启动异步 2、在具体实现异步的方法上添加Async注解 package com.example.demo;import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootAppli…...
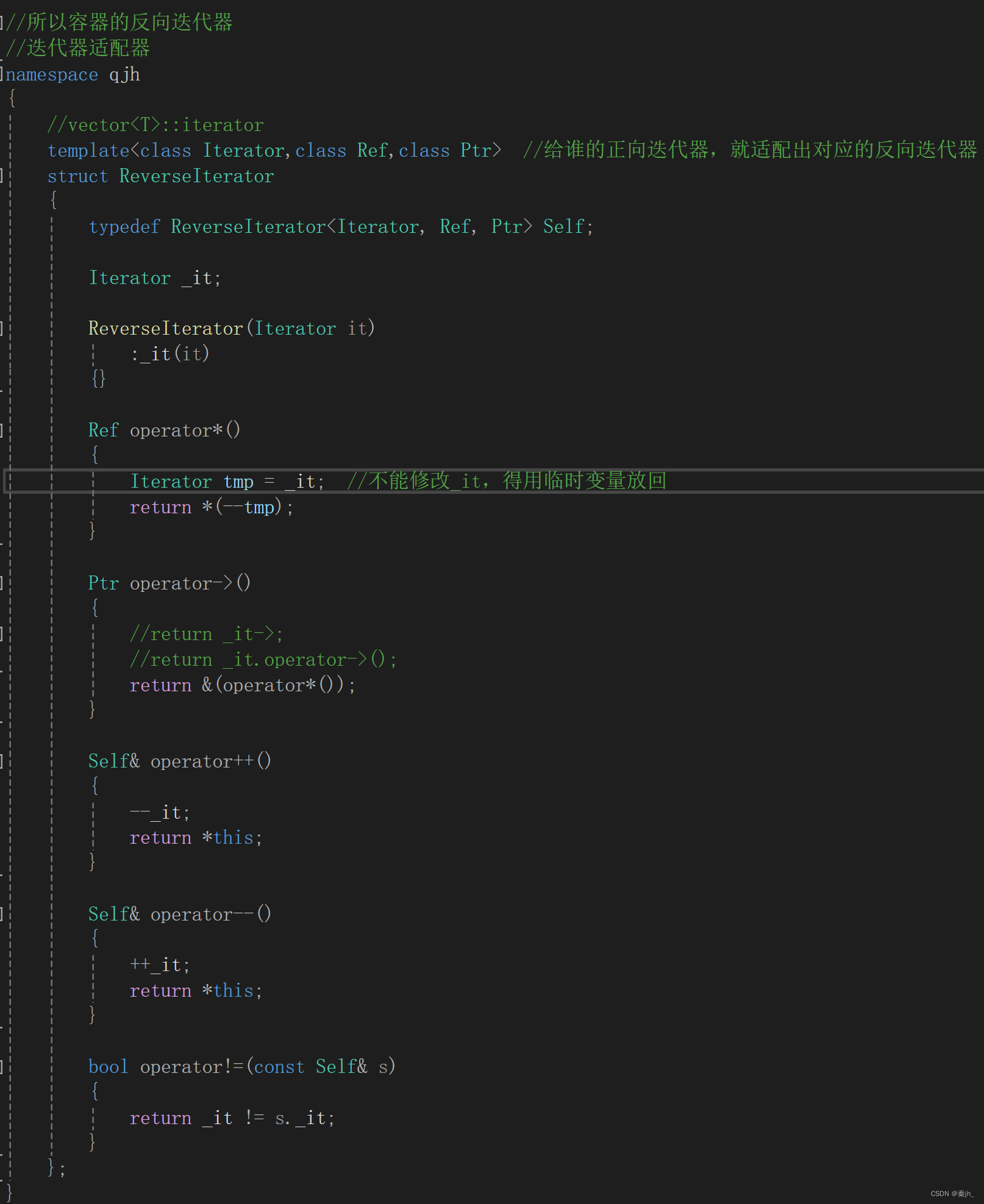
【C++/STL】list(常见接口、模拟实现、反向迭代器)
🌈个人主页:秦jh_-CSDN博客🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12575764.html?spm1001.2014.3001.5482 目录 前言 list的常见接口 对迭代器的封装 节点 重载-> const迭代器 list与vector的对比 反向迭代…...

wms中对屏幕进行修改wm size设置屏幕宽高原理剖析
背景: 上面是正常屏幕1440x2960的屏幕大小,如果对display进行相关的修改,可以使用如下命令: adb shell wm size 1080x1920 得出如下的画面 明显看到差异就是屏幕上下有黑边了,那么下面就来调研这个wm size是怎么做的…...
java面试题及答案2024,java2024最新面试题及答案(之一)
发现网上很多Java面试题都没有答案,所以花了很长时间搜集整理出来了这套Java面试题大全,希望对大家有帮助哈~ 本套Java面试题大全,全的不能再全,哈哈~ 一、Java 基础 1. JDK 和 JRE 有什么区别? JDK:Ja…...
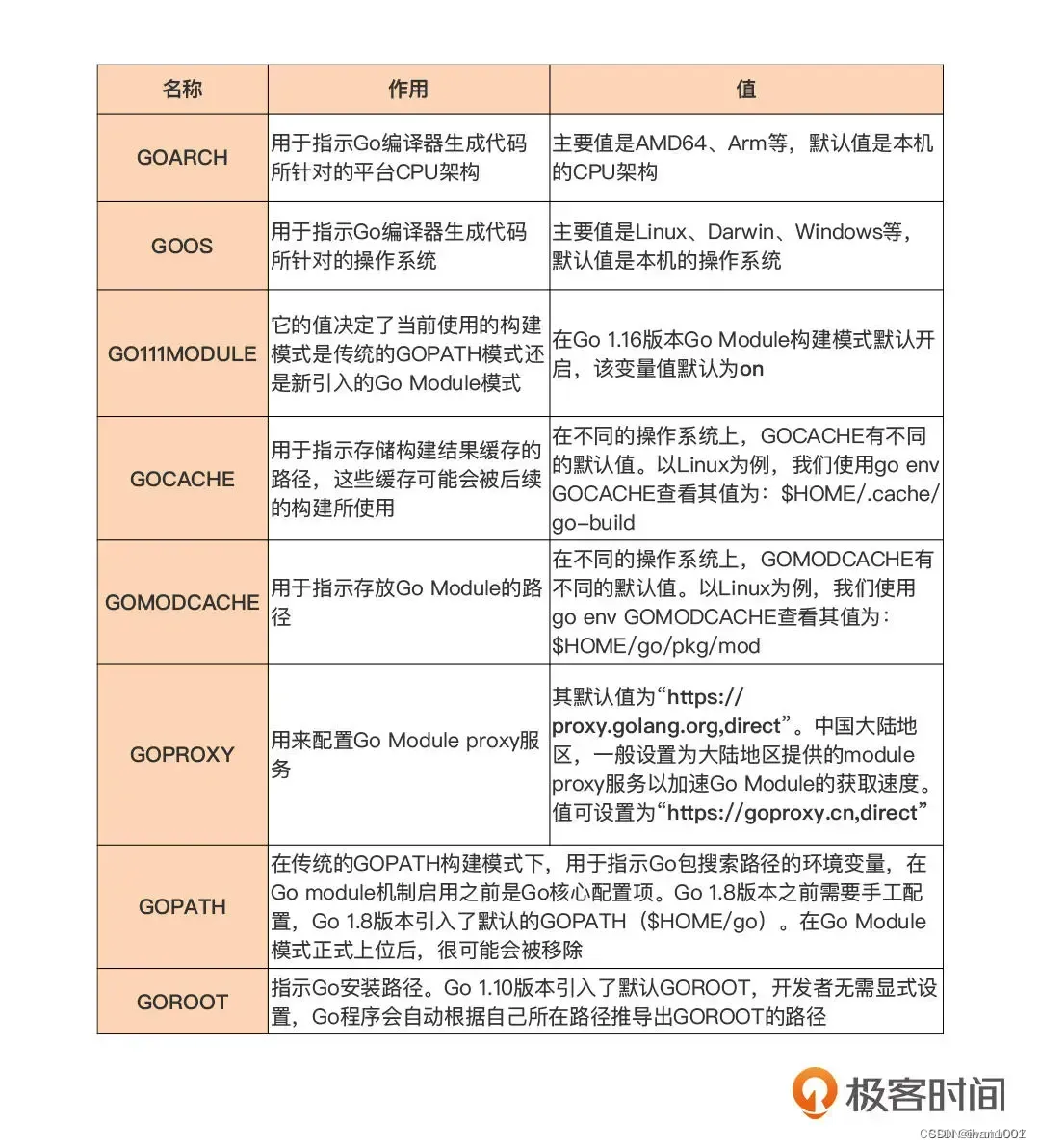
Go Modules 使用
文章参考https://blog.csdn.net/wohu1104/article/details/110505489 不使用Go Modules,所有的依赖包都是存放在 GOPATH /pkg下,没有版本控制。如果 package 没有做到完全的向前兼容,会导致多个项目无法运行(包版本需求不同)。 于是推出了g…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
