【一百】【算法分析与设计】N皇后问题常规解法+位运算解法
N皇后问题
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
题目描述
给出一个n×nn\times nn×n的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。
输入描述:
一行,一个整数n(1≤n≤12)n(1\le n \le 12)n(1≤n≤12),表示棋盘的大小。
输出描述:
输出一行一个整数,表示总共有多少种摆放皇后的方案,使得它们两两不能互相攻击。
示例1
输入
复制4
4
输出
复制2
2
常规解法


#include<bits/stdc++.h>
using namespace std;#define int long long
#define endl '\n'
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);#define p pair<int,int>
#define ff first
#define ss second
#define pb push_back
#define ppb pop_back#define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从a到b的循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从a到b的倒序循环
#define tests() int t;cin>>t;while(t--) // 读取测试次数并循环int n; // 棋盘的大小
int ret=0; // 解的数量
vector<bool> visited1; // 列的标记数组
vector<bool> visited2; // 左下到右上的斜线标记数组
vector<bool> visited3; // 右下到左上的斜线标记数组void dfs(int i){ // 深度优先搜索函数,i表示当前行ltu(j,1,n){ // 遍历第i行的每一列if(!visited1[j]&&!visited2[j-i+n]&&!visited3[j+i]){ // 如果第j列和两条斜线都没有被占用if(i==n){ // 如果已经放到最后一行ret++; // 解的数量加一continue; // 继续下一次循环}visited1[j]=visited2[j-i+n]=visited3[j+i]=true; // 标记当前列和斜线dfs(i+1); // 递归调用下一行visited1[j]=visited2[j-i+n]=visited3[j+i]=false; // 回溯,取消标记}}
}void solve(){ // 解决函数ret=0; // 重置解的数量visited1.assign(n+1,0); // 初始化列标记数组visited2.assign(2*n+1,0); // 初始化左下到右上的斜线标记数组visited3.assign(2*n+1,0); // 初始化右下到左上的斜线标记数组dfs(1); // 从第一行开始搜索cout<<ret<<endl; // 输出解的数量
}signed main(){ // 主函数Fast(); // 加速输入输出cin>>n; // 读取棋盘大小solve(); // 调用解决函数
}
位运算解法1

#include<bits/stdc++.h>
using namespace std;#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义 endl 为换行符
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 快速输入输出#define p pair<int,int> // 定义 p 为一对整数
#define ff first // 定义 ff 为 first
#define ss second // 定义 ss 为 second #define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从 a 到 b 的递增循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从 a 到 b 的递减循环
#define tests() int t;cin>>t;while(t--) // 定义测试次数循环int n; // 定义 n
int ret=0; // 定义 ret 并初始化为 0
int col, leftt, rightt; // 定义 col, leftt, rightt 记录有皇后的位置// 深度优先搜索函数
void dfs(int i, int col, int leftt, int rightt) {if (i == n + 1) { // 如果已经放置完所有皇后ret++; // 计数增加return; // 返回上一层}// 从第 0 列到第 n-1 列尝试放置皇后ltu(j, 0, n-1) {// 检查第 j 列,左斜和右斜是否被攻击bool temp = (col & (1 << j)) | (leftt & (1 << (i - j + n))) | (rightt & (1 << (i + j)));if (!temp) { // 如果当前位置没有被攻击// 递归调用下一行,更新 col, leftt 和 righttdfs(i + 1, col | (1 << j), leftt | (1 << (i - j + n)), rightt | (1 << (i + j)));}}
}// 解决问题的函数
void solve() {col = leftt = rightt = 0; // 初始化 col, leftt 和 righttdfs(1, col, leftt, rightt); // 调用 dfs 函数从第 1 行开始cout << ret << endl; // 输出结果
}signed main() {Fast(); // 快速输入输出cin >> n; // 输入 nsolve(); // 调用 solve 函数
}
位运算解法2

#include<bits/stdc++.h>
using namespace std;#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义 endl 为换行符
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 快速输入输出#define p pair<int,int> // 定义 p 为一对整数
#define ff first // 定义 ff 为 first
#define ss second // 定义 ss 为 second
#define pb push_back // 定义 pb 为 push_back
#define ppb pop_back // 定义 ppb 为 pop_back#define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从 a 到 b 的递增循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从 a 到 b 的递减循环
#define tests() int t;cin>>t;while(t--) // 定义测试次数循环int n; // 定义 n
int ret=0; // 定义 ret 并初始化为 0
int col,leftt,rightt; // 定义 col, leftt, rightt 记录有皇后的位置
int aim=0; // 定义 aim 并初始化为 0// 深度优先搜索函数
void dfs(int i,int col,int leftt,int rightt){int temp=col|leftt|rightt; // 计算当前所有被攻击的位置temp=~temp; // 取反得到可以放置皇后的位置temp&=aim; // 只保留有效位// 当 temp 不为 0 时while(temp){int lowbit=temp&(-temp); // 取出最低位的 1temp^=lowbit; // 将最低位的 1 置为 0if(i==n){ // 如果已经到最后一行ret++; // 计数增加continue; // 继续下一步}// 递归调用下一行,更新 col, leftt 和 righttdfs(i+1,col|lowbit,(leftt|lowbit)<<1,(rightt|lowbit)>>1);}}// 解决问题的函数
void solve(){ret=0; // 初始化 retcol=leftt=rightt=0; // 初始化 col, leftt 和 righttaim=(1<<n)-1; // 初始化 aim,将前 n 位设为 1dfs(1,col,leftt,rightt); // 调用 dfs 函数从第 1 行开始cout<<ret<<endl; // 输出结果
}signed main(){Fast(); // 快速输入输出cin>>n; // 输入 nsolve(); // 调用 solve 函数}
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【一百】【算法分析与设计】N皇后问题常规解法+位运算解法
N皇后问题 链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 给出一个nnn\times nnn的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同…...

GPT-4:人工智能领域的新里程碑
近期,OpenAI推出了备受瞩目的GPT-4。作为GPT系列的最新成员,GPT-4在自然语言处理(NLP)领域再次刷新了记录,引发了广泛的关注和讨论。在试用GPT-4之后,我深感其在技术能力、应用场景等方面都取得了显著的进步…...

mysql inset bug
在 SQL 中,日期值需要用单引号包围,这是因为 SQL 将日期值视为字符串格式。数据库引擎在处理这些值时会将它们解析为适当的日期类型。如果不使用单引号,数据库引擎会将它们视为数字或列名,从而导致语法错误。 日期格式 MySQL 支…...

oracle查看序列
在Oracle数据库中,查看序列的方式主要有以下几种: 查看当前用户下的所有序列名称: sql复制代码 SELECT sequence_name FROM user_sequences; 查看所有用户的序列: sql复制代码 SELECT sequence_name FROM all_sequences; 查看…...
flask-slqalchemy使用详解
目录 1、flask-sqlalchemy 1.1、flask_sqlalchemy 与sqlalchemy 的关系 1.1.1、 基本定义与用途 1.2、flask_sqlalchemy 的使用 1.2.1、安装相关的库 1.2.2、项目准备 1.2.3、创建ORM模型 1.2.3.1、使用db.create_all()创建表的示例 1.2.3.2、创建多表关联ORM模型 1.…...

Scala学习笔记8: 包
目录 第八章 包1- 包2- 包的作用域3- 串联式包语句4- 包对象5- 引入end 第八章 包 在Scala中, 包(Package) 用于组织和管理代码, 类似与 Java 中的包 ; 包可以包含类、对象、特质等Scala代码, 并通过层次结构来组织代码 ; 可以使用 package 关键字来定义包, 并使用 . 来表示…...

分享一份糟糕透顶的简历,看看跟你写的一样不
最近看了一个人的简历,怎么说呢,前几年这么写没问题,投出去就有回复,但从现在开始,这么写肯定不行了。下面我给大家分享一下内容: 目录 🤦♀️这是简历文档截图 🤷♀️这是基本…...
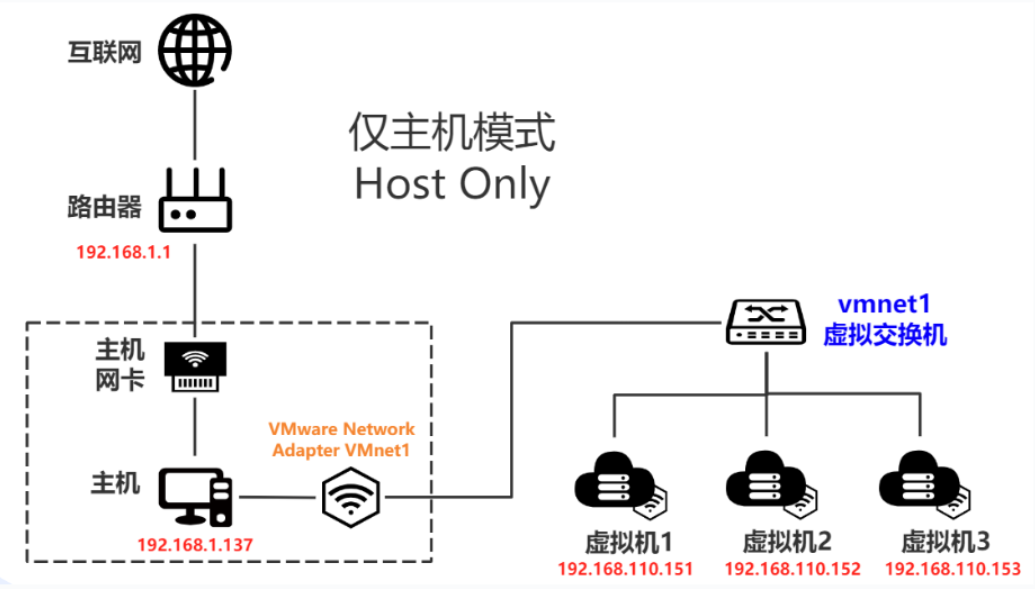
VMware 三种网络模式
目录 一、网卡、路由器、交换机 二、虚拟网络编辑器 三、网络模式 1.桥接模式 通信方式 特点 配置 连通情况 使用场景 2.NAT模式 通信方式 特点 配置 连通情况 使用场景 3.仅主机 通信方式 特点 配置 连通情况 使用场景 一、网卡、路由器、交换机 网卡(Ne…...

红绿二分查找
《英雄算法零基础》之 二分查找 https://articles.zsxq.com/id_ib4xgs0cogic.html 在写模版之前我们先搞清楚二分查找是怎样运行的,我们把一个数组分成红绿两种颜色,可以理解为绿色就是符合情况的,红色就是不符合情况的(类似红绿灯…...
C51单片机 串口打印printf重定向
uart.c文件 #include "uart.h"void UartInit(void) //4800bps11.0592MHz {PCON | 0x80; //使能波特率倍速位SMODSCON 0x50; //8位数据,可变波特率。使能接收TMOD & 0x0F; //清除定时器1模式位TMOD | 0x20; //设定定时器1为8位自动重装方式TL1 0xF4; //设…...
PieCloudDB Database Flink Connector:让数据流动起来
面对客户环境中长期运行的各种类型的传统数据库,如何优雅地设计数据迁移的方案,既能灵活地应对各种数据导入场景和多源异构数据库,又能满足客户对数据导入结果的准确性、一致性、实时性的要求,让客户平滑地迁移到 PieCloudDB 数据…...

主机CPU访问PCIe设备内存空间和PCIe设备访问主机内存空间
在x86体系架构中,主机CPU访问PCIe设备内存空间和PCIe设备访问主机内存空间的过程涉及多个层次的地址映射和转换。以下是详细的解释: 主机CPU访问PCIe设备内存空间 1. CPU生成虚拟地址(Virtual Address, VA): 在x86架构中&#…...

在家AIAA(美国航空航天学会)文献如何查找下载
今天有位同学的求助文献来自AIAA(美国航空航天学会),下面就讲一下不用求助他人自己就可搞定文献下载的途径并实例操作演示。 首先我们先对AIAA(美国航空航天学会)数据库做个简单的了解: 美国航空航天学会…...

dnf手游版游玩感悟
dnf手游于5月21号正式上线,作为一个dnf端游老玩家,并且偶尔上线ppk,自然下载了手游版,且玩了几天。 不得不说dnf手游的优化做到了极好的程度。 就玩法系统这块,因为dnf属于城镇地下城模式,相比…...
安卓如何书写注册和登录界面
一、如何跳转一个活动 左边的是本活动名称, 右边的是跳转界面活动名称 Intent intent new Intent(LoginActivity.this, RegisterActivity.class); startActivity(intent); finish(); 二、如果在不同的界面传递参数 //发送消息 SharedPreferences sharedPreferen…...

黄仁勋的AI时代:英伟达GPU革命的狂欢与挑战
在最近的COMPUTEX 2024大会上,英伟达创始人黄仁勋发布了最新的Blackwell GPU。这次发布不仅标志着英伟达在AI领域的又一次飞跃,也展示了其对未来技术发展的战略规划。本文将详细解析英伟达最新技术的亮点,探讨其在AI时代的市场地位和未来挑战…...

Linux云计算架构师涨薪班课程内容包含哪些?
第一阶段:Linux云计算运维初级工程师 目标 云计算工程师,Linux运维工程师都必须掌握Linux的基本功,这是一切的根本,必须全部掌握,非常重要,有了这些基础,学习上层业务和云计算等都非常快&#x…...
c语言:自定义类型(枚举、联合体)
前言: c语言中中自定义类型不仅有结构体,还有枚举、联合体等类型,上一期我们详细讲解了结构体的初始化,使用,传参和内存对齐等知识,这一期我们来介绍c语言中的其他自定义类型枚举和联合体的知识。 1.位段 …...

2024年适合GISer参加的全国性比赛
作为一名GISer,在校期间参加GIS比赛,不仅能够锻炼和提升自己的GIS专业水平,例如软件操作、开发能力等;还能加强自己团队协作能力、组织能力和沟通能力,此外,还可以给简历加分,增强职场竞争力。 …...
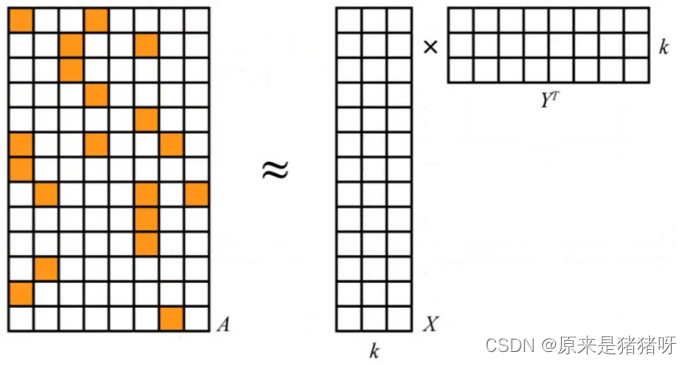
番外篇-用户购物偏好标签BP-推荐算法ALS
引言 推荐系统式信息过载所采用的措施,面对海量的数据信息,从中快速推荐出符合用户特点的物品。 推荐系统是自动化的通过分析用户对历史行为数据,完成用户的个性化建模,从而主动给用户推荐能够满足他们兴趣和需求的软件系统。 数…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
