LeetCode216组合总和3
题目描述
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:只使用数字1到9。每个数字 最多使用一次。返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
解析
递归加剪枝,搜索长度达到k就可以返回,另外当选择的数之和比n还大的时候就可以不用再搜索了。
public List<List<Integer>> combinationSum3(int k, int n) {List<List<Integer>> res = new ArrayList<>();boolean[] isChosen = new boolean[10];List<Integer> current = new ArrayList<>();DFS(res, current, isChosen, 0, k, n, 1);return res;}private void DFS(List<List<Integer>> res,List<Integer> current,boolean[] isChosen,int curSum,int k,int n,int start) {if(current.size() == k) {if(curSum == n) {res.add(new ArrayList<>(current));}return;}for(int i = start; i <= 9 ; i++) {if(!isChosen[i]) {current.add(i);curSum += i;if(curSum <= n) {isChosen[i] = true;DFS(res, current, isChosen, curSum, k, n, i + 1);}current.remove(current.size() - 1);curSum -= i;isChosen[i] = false; // 回溯}}}

相关文章:

LeetCode216组合总和3
题目描述 找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:只使用数字1到9。每个数字 最多使用一次。返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 解析 递归加剪枝,搜索长度达…...

微软找腾讯接盘,Windows直接安装手机APP体验起飞了
熟悉微软的同学都知道微软有个传统艺能——什么好用砍什么。 比如 Win10 砍掉了还算方便的小娜,推出 Win11 砍掉了 Win10 上面好用的磁贴功能等。 上一秒用户还在夸奖点赞。 下一秒就给你砍掉,顺带还塞一堆 BUG 给你。 但没办法,PC 近乎垄断…...
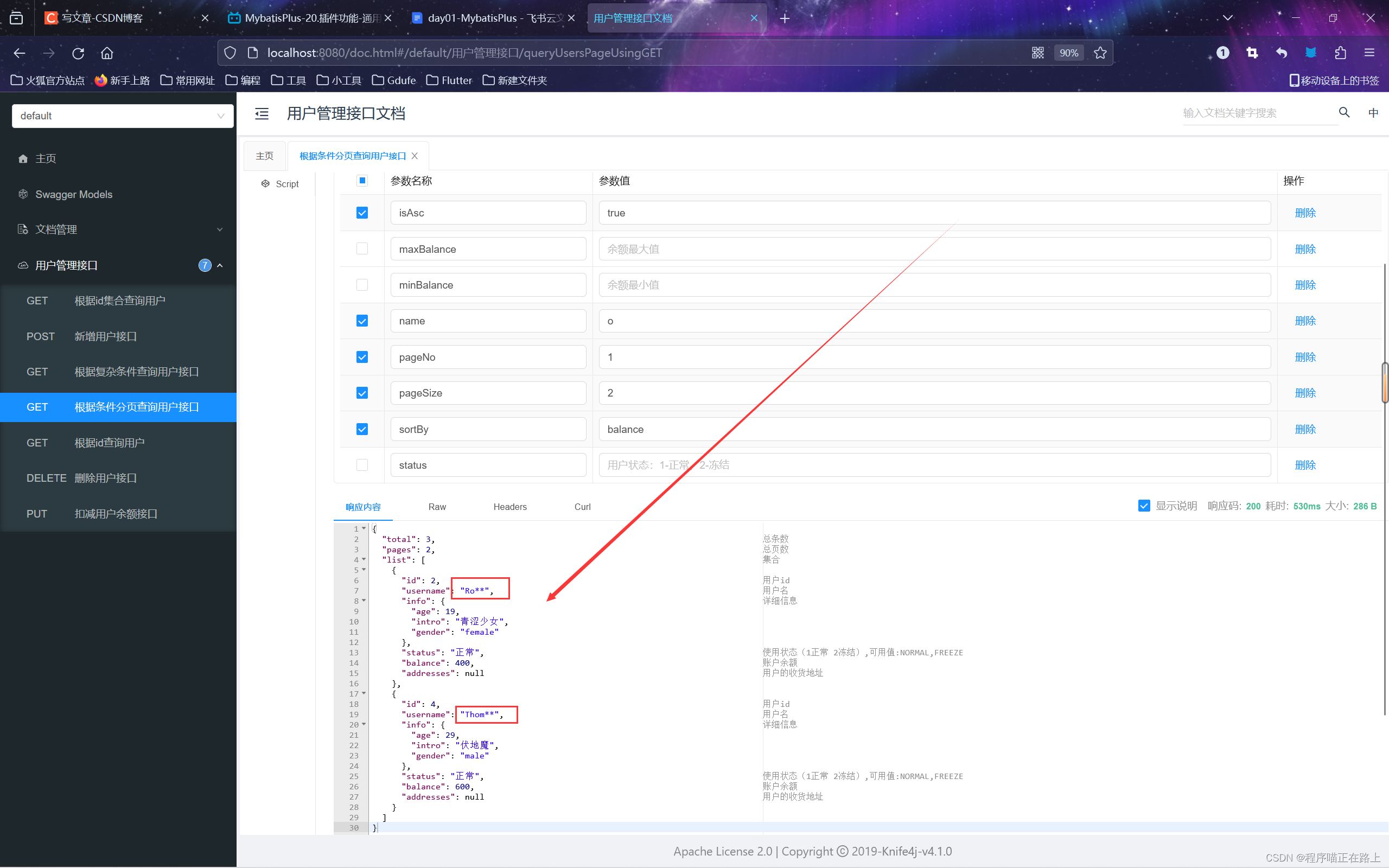
【Springcloud微服务】MybatisPlus下篇
🔥 本文由 程序喵正在路上 原创,CSDN首发! 💖 系列专栏:Springcloud微服务 🌠 首发时间:2024年6月4日 🦋 欢迎关注🖱点赞👍收藏🌟留言ὃ…...
i18n-demo
一、demo 1、资源文件准备 如我需要对menu、logMsg内容做国际化。 resources下放各个语言文件,直接放resources下都行。我是新建了一个myi18n文件夹, (1)然后在myi18n上点击New--Resource Bundle (2)在…...

[Leetcode] 0-1背包和完全背包
46. 携带研究材料 纯01背包(非应用):只能选择一次物品 dp[j]:容量为j的背包所能装的最大容量 容量需要倒序 416. 分割等和子集 能否装满 dp[j]:容量为j的背包所能装的最大容量 1049. 最后一块石头的重量 II 尽可…...

自定义类型:联合体和枚举
1. 联合体类型的声明 2. 联合体的特点 3. 联合体大小的计算 4. 枚举类型的声明 5. 枚举类型的优点 6. 枚举类型的使用 欢迎关注 熬夜学编程 创作不易,请多多支持 感谢大家的阅读、点赞、收藏和关注 如有问题,欢迎指正 1. 联合体 1.1 联合体类型的声…...

【Cityengine】Cityengine生产带纹理的建筑模型导入UE4/UE5(下)
【Cityengine】Cityengine生产带纹理的建筑模型导入UE4/UE5(下) 一、导出数据(2022中文版案例)二、安装datasmith插件三、导入数据四、检查导入材质是否正常五、编辑替换材质六、安装模型编辑插件七、编辑替换建筑规则 一、导出数…...

详解51种企业应用架构模式
导读:企业应用包括哪些?它们又分别有哪些架构模式?世界著名软件开发大师Martin Fowler给你答案 01、什么是企业应用 我的职业生涯专注于企业应用,因此,这里所谈及的模式也都是关于企业应用的。(企业应用还…...

【十年java搬砖路】Jumpserver docker版安装及配置Ldap登陆认证
Jumpserver docker 安装启动教程 拉取镜像 docker pull JumpServer启动进行前确保有Redis 和Mysql 创建jumperServer数据库 在MYSQL上执行 创建数据库 登陆MYSQL mysql -u root -p 创建Jumperserveri库 create database jumpserver default charset utf8mb4;可以为jumperSe…...

C\C++内存管理(未完结)
文章目录 一.C\C内存分布二.C语言中动态内存管理方式:malloc/calloc/realloc/free三.C内存管理方式3.1.new/delete操作内置类型3.2.new和delete操作自定义类型 四.operator new与operator delete函数(重要点进行讲解)4.1. operator new与oper…...
——抽象与接口)
一个小时搞定JAVA面向对象(5)——抽象与接口
文章目录 抽象抽象的注意事项static\final\private是否可以修饰抽象方法继承和抽象知识点回顾 接口接口实现总结抽象方法默认方法静态方法成员变量接口的特点接口和抽象类的区别 抽象 关键字: abstract 抽象方法: 修饰符 abstract 返回值类型 方法名(参数); 抽象类: public a…...

图像关键特征描述方法-小目标
图像关键特征描述方法主要包括以下几种: SIFT(尺度不变特征变换): SIFT是一种广泛使用的特征描述方法,它通过尺度空间和梯度方向直方图来描述图像中的关键点。SIFT特征描述具有尺度不变性和旋转不变性,对于光照和视角变化也具有一定的鲁棒性。 SURF(加速稳健特征): SURF…...
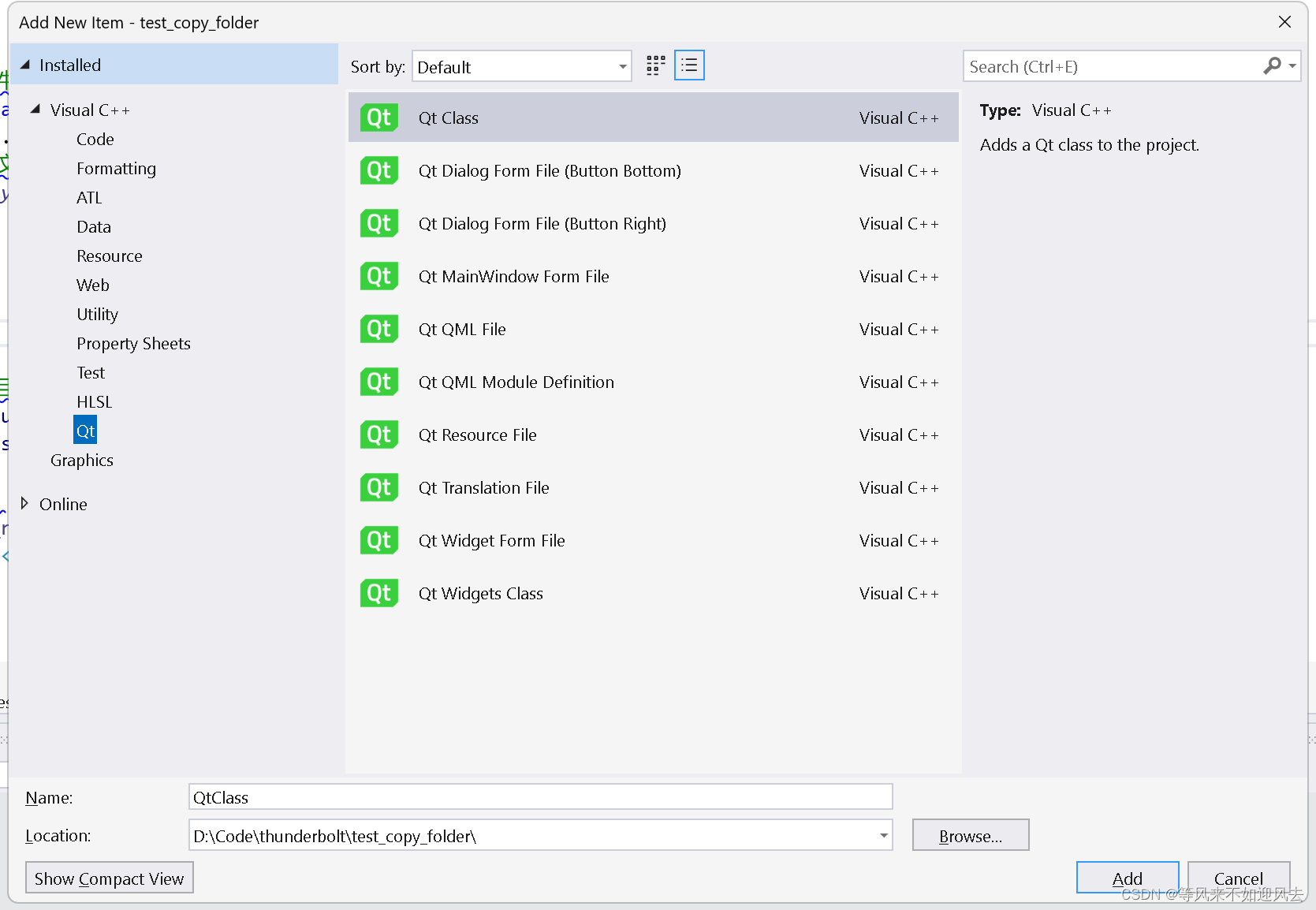
【qt15】windeployqt 安装依赖
debug模式vs可以使用qt插件新建qt文件 D:\Qt15\5.15.2\msvc2019\bin\windeployqt.exe Warning: Cannot find Visual Studio installation directory, VCINSTALLDIR is not set.D:\Qt15\5.15.2\msvc2019\bin\windeployqt.exe .\filecopier.exeWindows PowerShell Copyright (C) …...
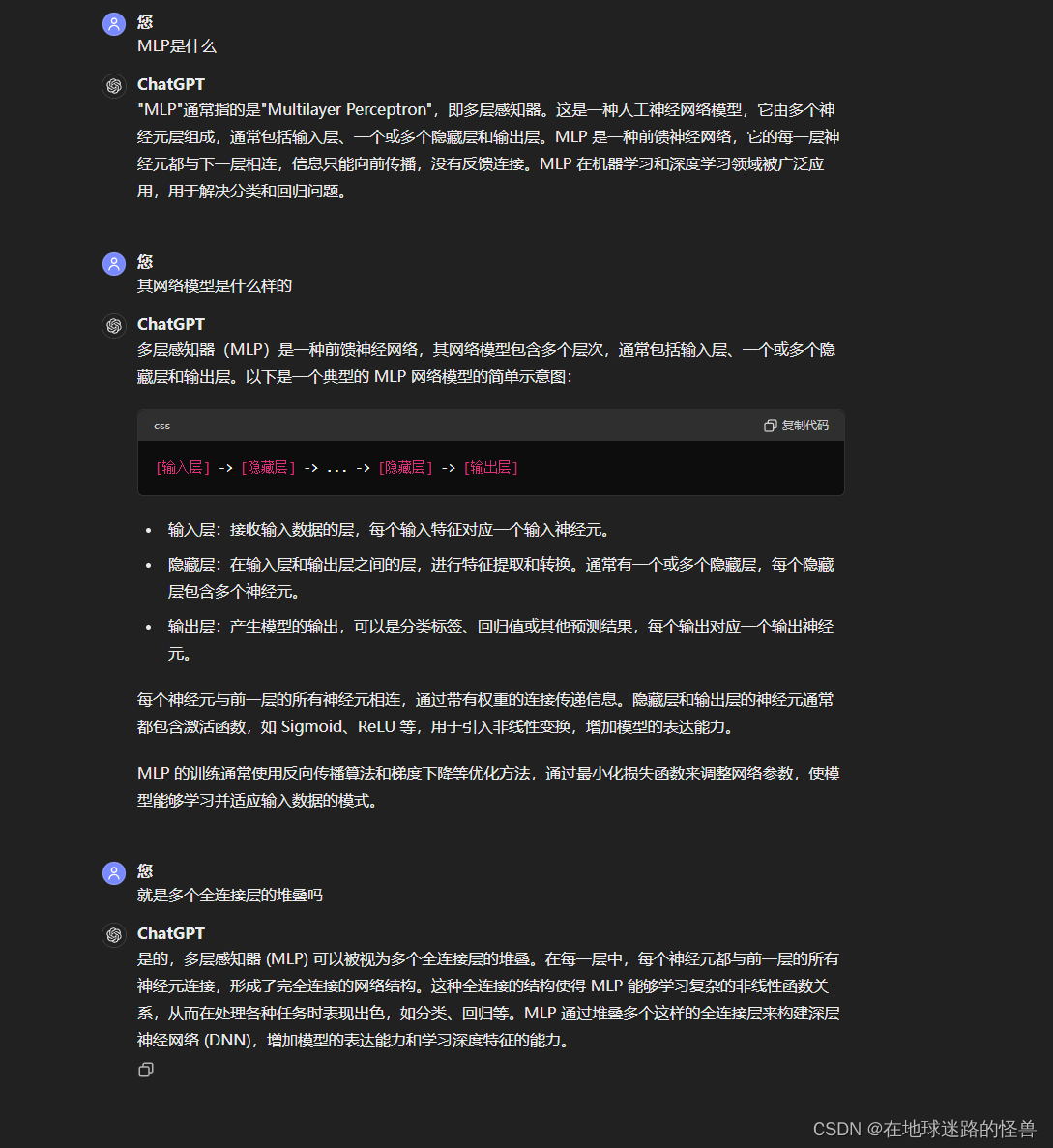
DETR论文重点
DETR就是 DEtection TRansformer 的缩写。 论文原名:End-to-End Object Detection with Transoformers。 重点有两个:端到端、Transformer结构 论文概述 注意:斜体的文字为论文原文,其他部分内容则是为增进理解而做的解释。 …...
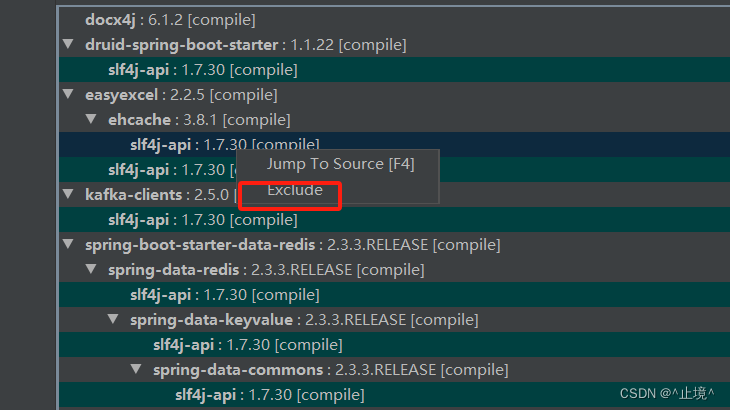
slf4j等多个jar包冲突绑定的排查方法使用IDEA的maven help解决
1.安装 2.使用maven help解决,找到对应包存在的冲突 使用exclude直接解决即可...

MySQL主从的延迟怎么解决呢?
以下是一些减少或解决MySQL主从延迟的策略: 优化查询和索引: 确保所有的查询都经过优化,以减少主服务器上的负载。使用合适的索引来加速查询速度,减少锁的时间。 分散复制负载: 使用多个从服务器分散读取负载。使用并…...
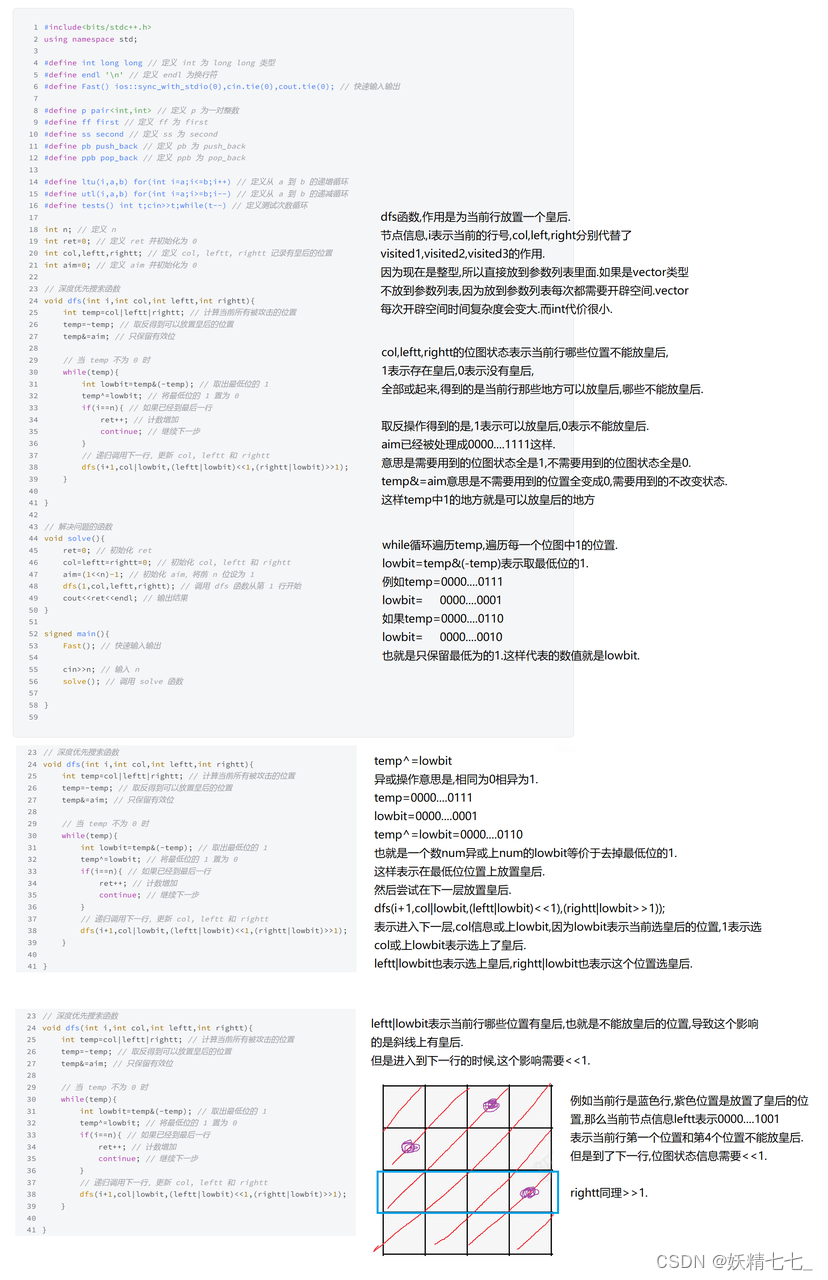
【一百】【算法分析与设计】N皇后问题常规解法+位运算解法
N皇后问题 链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 给出一个nnn\times nnn的国际象棋棋盘,你需要在棋盘中摆放nnn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同…...

GPT-4:人工智能领域的新里程碑
近期,OpenAI推出了备受瞩目的GPT-4。作为GPT系列的最新成员,GPT-4在自然语言处理(NLP)领域再次刷新了记录,引发了广泛的关注和讨论。在试用GPT-4之后,我深感其在技术能力、应用场景等方面都取得了显著的进步…...

mysql inset bug
在 SQL 中,日期值需要用单引号包围,这是因为 SQL 将日期值视为字符串格式。数据库引擎在处理这些值时会将它们解析为适当的日期类型。如果不使用单引号,数据库引擎会将它们视为数字或列名,从而导致语法错误。 日期格式 MySQL 支…...

oracle查看序列
在Oracle数据库中,查看序列的方式主要有以下几种: 查看当前用户下的所有序列名称: sql复制代码 SELECT sequence_name FROM user_sequences; 查看所有用户的序列: sql复制代码 SELECT sequence_name FROM all_sequences; 查看…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
