【数据结构】穿梭在二叉树的时间隧道:顺序存储的实现
专栏引入
哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我想让大家知道的是:数据结构非常有趣,很多算法是智慧的结晶,我希望大家在学习数据结构的过程是一种愉悦的心情感受。因此我开创了《数据结构》专栏,在这里我将把数据结构内容以有趣易懂的方式展现给大家。
1.二叉树的顺序存储结构
之前我们谈过了树的存储结构,并且谈到了顺序存储结构对树这种一对多的关系结构实现起来还是比较困难的。但二叉树是一种特殊的树,由于二叉树的特殊性,使得它可以使用顺序存储结构来实现,二叉树的顺序存储结构就是使用一维数组存储二叉树中的节点,并且节点的存储位置,也就是数组的下标要能体现出来节点之间的逻辑关系,比如:双亲和孩子的关系、左孩子右兄弟的关系等。先来看看完全二叉树的顺序存储,就用下面这棵二叉树为例:

将这棵二叉树存入数组中,相应的下标对应其同样的位置,很多数据结构相关书籍上下标都是将0空置,从1开始存储,其实下标0的位置是否存放数据对堆的实现的难度没有影响,为了节省空间我对下标为0的位置进行了存储,如下图:
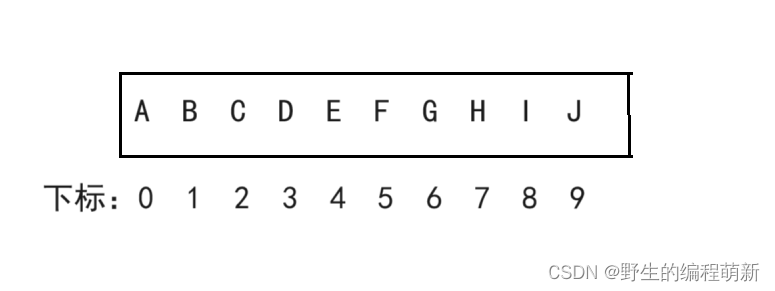
这下我们可以看出来完全二叉树的优越性了吧,由于它严格的定义,所以用顺序结构也可以表现出二叉树的结构来,当然对于一般的二叉树,尽管层序编号不能反映出来逻辑关系,但是可以将其按完全二叉树来编号,只不过,把不存在的节点设置为"NULL"而已,就像下面的图中,虚线部分表示不存在:


我们再考虑一种极端的情况:一颗深度为h的右斜树。它只有h个节点,却要分配个存储单元空间,这显然是对存储空间的浪费,如下图所示:
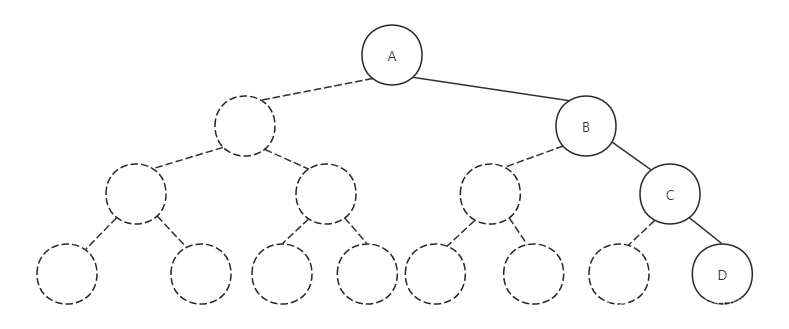

所以,二叉树的顺序存储结构一般只适用于完全二叉树。上一篇中我们提到了堆是一个特殊的完全二叉树,所以这篇我们就以堆为例子来实现二叉树的顺序存储。
2.堆
2.1堆的概念
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子节点的值,称为大顶堆;或者每个结点的值都小于等于其左右孩子结点的值,称为小顶堆。如下图所示:

从堆的定义可以知道:根节点一定是堆中所有结点的最大(小)值 。在上一篇堆二叉树的性质介绍时,有一个性质还没和大家介绍,因为这个性质就仿佛是为堆量身定制的,所以我计划在介绍堆时再介绍它:
如果一棵有n个节点的完全二叉树(其深度为)的节点按层序编号(从第一层到第
层,每层从左到右),对任一节点i(1≤i≤n)有:
- 如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则双亲是节点
。
- 如果2i>n,则节点i没有左孩子(节点i为叶子节点),否则其左孩子是节点2i。
- 如果2i+1>n,则节点i没有右孩子;否则其右孩子是节点2i+1。
在这个性质第二、三条,也就是说明下标i与2i和2i+1的双亲子女的关系:双亲结点=(子节点-1)/2。
2.2堆的实现
我们先来定义一下堆的结构:
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;2.2.1堆的创建和销毁
堆的创建我们使用顺序存储来实现,所以它的创建和销毁的实现代码和顺序表的实现的相同。首先是堆的创建函数:
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}接着是堆的销毁函数:
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}2.2.2堆的向上调整
一说到调整我们肯定会对两个数据进行交换,我们先来写一个交换函数:
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}堆的向上调整是将一个元素插入到小堆时,调整堆的结构,使其满足小堆的性质过程。实现堆的向上调整的要先将元素插入到数组的最后一个位置(这一步我们在堆的插入操作中实现)。这时候我们就要比较插入元素和其双亲结点的大小关系,然后做出调整。这里我们可以用循环实现,用循环来实现比用递归实现的好处有:
- 空间开销:循环实现通常比递归实现需要更少的内存空间。递归函数会在每次调用时创建一个新的函数栈帧,而循环则只使用一个循环体内的局部变量。
- 性能:循环实现通常比递归实现具有更高的执行效率。递归函数在每次调用时都需要进行函数调用、参数传递和返回值处理等操作,而循环通过使用迭代变量和循环条件判断来控制流程,避免了递归带来的额外开销。
首先我们先将这个函数里面的判断条件先写好:
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}既然我们要用循环来实现,那么使用while()语句的循环条件是什么呢?最坏的情况就是将新插入的节点经过调整变成根节点,那条件是parent≥0吗?parent是不会小于0的,当parent=0时,插入的数据还要接着向上调整交换,此时child变为0,parent=(0-1)/2,我们计算出来的parent时-0.5,但是要取整,所以parent还是0,此时循环还是没结束,会再次进入循环,此时child==parent,经过判断语句会侥幸跳出循环,这样是不严谨的。我们将循环条件设为child大于0就可以完美解决这个问题。此时,这个向上调整的操作完整代码为:
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}2.3堆的插入
堆的插入操作和顺序表的插入操作相似,其具体步骤为:
- 首先,函数开始时先进行一些边界判断,确保堆的指针有效。
- 如果堆的当前元素数量等于堆的容量,即堆已满,需要进行动态扩容。这里使用realloc函数对堆的数组进行扩容,新的容量为原来容量的两倍。
- 将待插入的元素x放到堆数组的最后一个位置,并将堆的元素数量递增。
- 调用AdjustUp函数对刚插入的元素进行向上调整,保持堆的性质。
我们来实现一下这个操作:
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}2.4堆的向下调整
堆的向上调整是为了让堆在插入数据时能够保持堆的性质,而堆的向下调整操作是在删除根节点后,为了维护堆的性质而进行的操作。该操作的目的是将新的根节点下沉到合适的位置,使得根节点的值不大于它的左右子节点的值。堆的向下调整具体步骤为:
- 初始化子节点的索引child,设为父节点的左孩子节点的索引,即parent*2+1。
- 进入一个循环,判断当前节点是否有左孩子节点,如果有则执行循环体。
- 在循环体内,先假设左孩子节点的值最小,将child设为左孩子节点的索引。
- 检查右孩子节点是否存在,即child+1<size,如果存在且右孩子节点的值小于左孩子节点的值,则将child更新为右孩子节点的索引。
- 检查当前节点的值是否大于最小的子节点的值,如果是,则交换当前节点和最小子节点的值,将当前节点的索引设为子节点的索引child,并更新子节点的索引为新的左孩子节点的索引child=parent*2+1。
- 如果当前节点的值不大于最小子节点的值,即a[child]>=a[parent],则跳出循环。
- 重复之前的步骤,直到当前节点没有左孩子节点为止。
我们来具体实现一下这个操作:
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假设左孩子小,如果解设错了,更新一下if (child+1 < size && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}2.5堆的删除
堆的删除具体操作步骤为:
- 调用Swap函数来交换小堆根节点(php->a[0])和最后一个节点(php->a[php->size - 1])的值。这样就将要删除的根节点移到了最后一个位置。
- 将小堆的大小减1,即php->size--,表示删除了一个节点。
- 最后,调用AdjustDown函数来对小堆进行向下调整,以维护小堆的性质。这样就完成了小堆的删除操作。
我们来实现一下这个操作:
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}相关文章:
【数据结构】穿梭在二叉树的时间隧道:顺序存储的实现
专栏引入 哈喽大家好,我是野生的编程萌新,首先感谢大家的观看。数据结构的学习者大多有这样的想法:数据结构很重要,一定要学好,但数据结构比较抽象,有些算法理解起来很困难,学的很累。我想让大家…...

【数据结构与算法 经典例题】链表的回文结构(图文详解)
💓 博客主页:倔强的石头的CSDN主页 📝Gitee主页:倔强的石头的gitee主页 ⏩ 文章专栏:《数据结构与算法 经典例题》C语言 期待您的关注 目录 一、问题描述 二、解题思路 三、C语言代码实现 一、问题描述 二、解…...
通过DirectML和ONNXRuntime运行Phi-3模型
更多精彩内容,欢迎关注我的公众号“ONE生产力”! 上篇我们讲到通过Intel Core Ultra系列处理器内置的NPU加速运行Phi-3模型,有朋友评论说他没有Intel处理器是否有什么办法加速Phi-3模型。通常,使用GPU特别是NVIDA的GPU加速AI模型…...

C语言经典例题-18
1.判断是不是字母 题目描述: KK想判断输入的字符是不是字母,请帮他编程实现。 输入描述: 多组输入,每一行输入一个字符。 输出描述: 针对每组输入,输出单独占一行,判断输入字符是否为字母,输出内容详见输出样例。 输…...

计算机网络之crc循环冗余校验、子网划分、rip协议路由转发表、时延计算、香浓定理 奈氏准则、TCP超时重传 RTO
crc循环冗余校验 异或运算 : 相同得0,相异得1 从多项式获取除数 在原数据的末端补0 , 0的个数等于最高次项的阶数 如果最后结果的有效位数较少时,前面应该补0,补到个数与阶位相同 子网划分 子网掩码:用于识别IP地址中的网络号和主机号的…...
揭秘高效人事财务对接新方案!
一、客户介绍 某生物医药科技有限公司是一家专注于生物创新药物研发与生产的科技型企业。公司的主要业务范围包括技术开发、技术服务、医学研究与试验发展、经济信息咨询、企业管理等。公司凭借其强大的技术实力、丰富的研发经验和优秀的团队阵容,在生物创新药领域…...
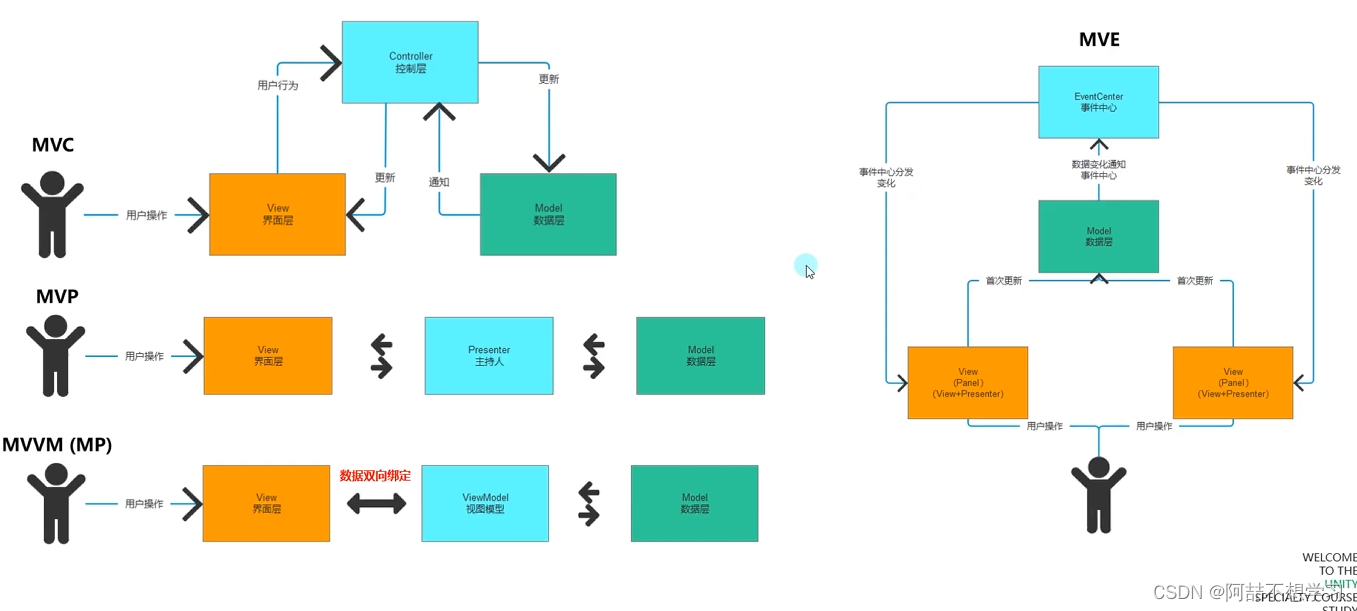
Unity中的MVC框架
基本概念 MVC全名是Model View Controller 是模型(model)-视图(view)-控制器(controller)的缩写 是一种软件设计规范,用一种业务逻辑、数据、界面显示 分离的方法组织代码 将业务逻辑聚集到一个部件里面,在改进和个性化定制界面及用户交互的同时&#x…...

网工内推 | 上市公司网工,Base广东,思科DE/IE认证优先
01 广州赛意信息科技股份有限公司 🔷招聘岗位:技术架构师 🔷职责描述: 1、设计、开发和维护工业数据库及其架构,包括数据采集、存储、处理和分析的工具和系统。 2、开发和维护数据管道和工作流程,确保数据…...
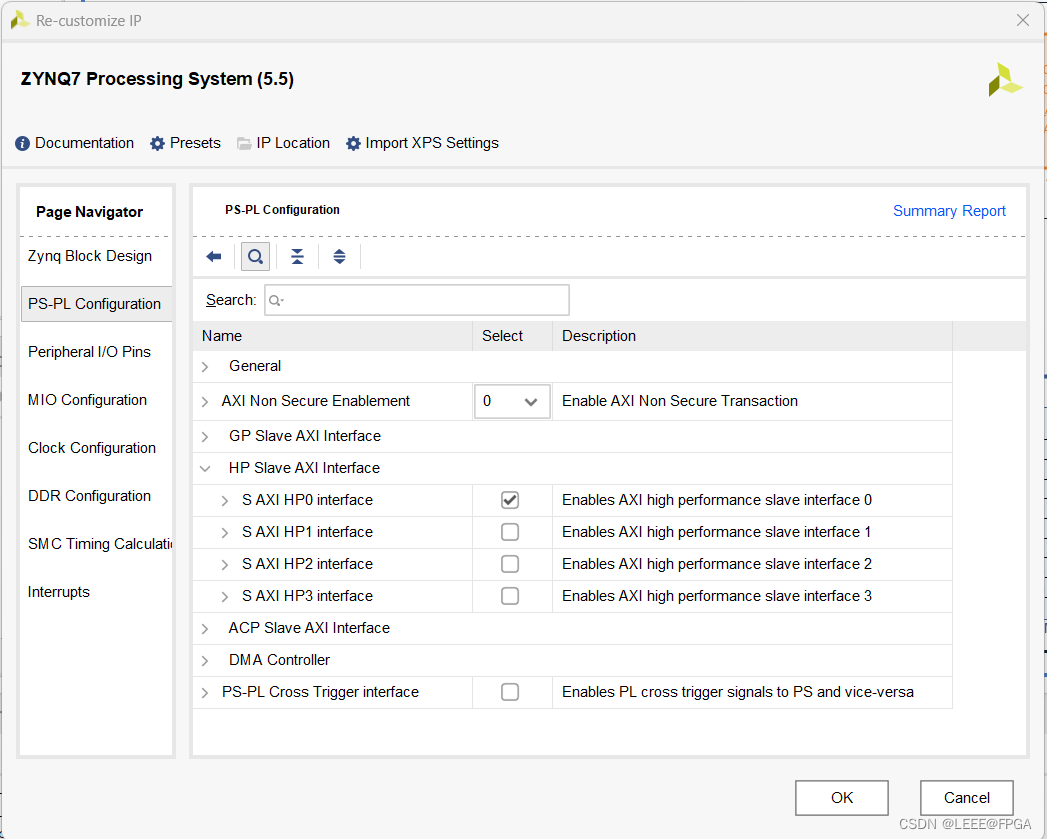
ZYNQ AXI4 FDMA内存读写
1 概述 如果用过ZYNQ的都知道,要直接操作PS的DDR 通常是DMA 或者VDMA,然而用过XILINX 的DMA IP 和 VDMA IP,总有一种遗憾,那就是不够灵活,还需要对寄存器配置,真是麻烦。对于我们搞 FPGA 的人来说,最喜欢直接了当,直接用FPGA代码搞定。现在XILINX 的总线接口是AXI4总线…...

签名安全规范:解决【请求对象json序列化时,时间字段被强制转换成时间戳的问题】
文章目录 引言I 签名安全规范1.1 签名生成的通用步骤1.2 签名运算(加密规则)1.3 对所有传入参数按照字段名的 ASCII 码从小到大排序(字典序)1.4 允许的请求头字段1.5 签名校验工具II 注解校验签名2.1 获取请求数据,并校验签名数据2.2 解决时间格式被强制转换成时间戳的问题…...

Web3.0区块链技术开发方案丨ICO与IDO代币开发
在Web3.0时代的到来下,区块链技术不仅改变着金融领域的格局,也在资金筹集和代币发行方面掀起了一场变革。初始代币发行(ICO)和去中心化代币发行(IDO)成为了项目融资的主要方式,其基于区块链技术…...
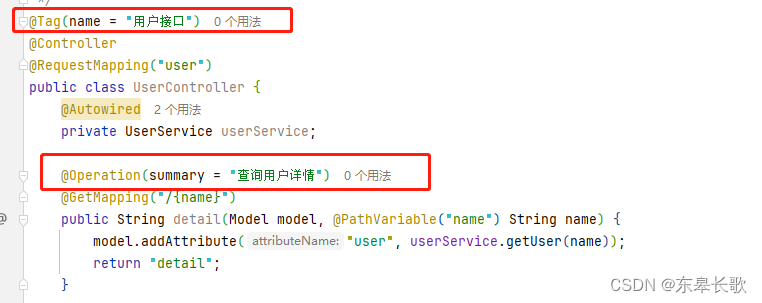
spring boot 3.x版本 引入 swagger2启动时报错
一,问题 Spring Boot 3.x版本的项目里,准备引入Swagger2作为接口文档,但是项目启动报错: java.lang.TypeNotPresentException: Type javax.servlet.http.HttpServletRequest not present at java.base/sun.reflect.generics.…...

华为机械工程师面试问题
在机械工程师的面试中,面试官可能会提出一系列问题,以评估应聘者的专业知识、技能、经验以及解决问题的能力。以下是一些可能的面试题: 基础知识与技能: 请解释机械工程中常用的几种传动方式,并比较它们的优缺点。描述一下你在机械设计过程中常用的软件,并举例说明你是如…...

一个简单并完整的springboot项目
一个简单并完整的springboot项目 项目地址1:https://download.csdn.net/download/qq_38234785/89398614 项目地址2:https://mbd.pub/o/buranxin/work 一、接口 curl --location --request POST http://localhost:8080/api/test \ --header Cookie: USER…...

SASS基础知识
什么是SASS 1. SASS与CSS的关系 SASS(Syntactically Awesome Stylesheets)是一种强大的CSS扩展语言,它允许开发者使用变量、嵌套规则、混合宏和更多功能,这些在纯CSS中是不可能做到的。SASS旨在简化CSS代码的维护,并…...
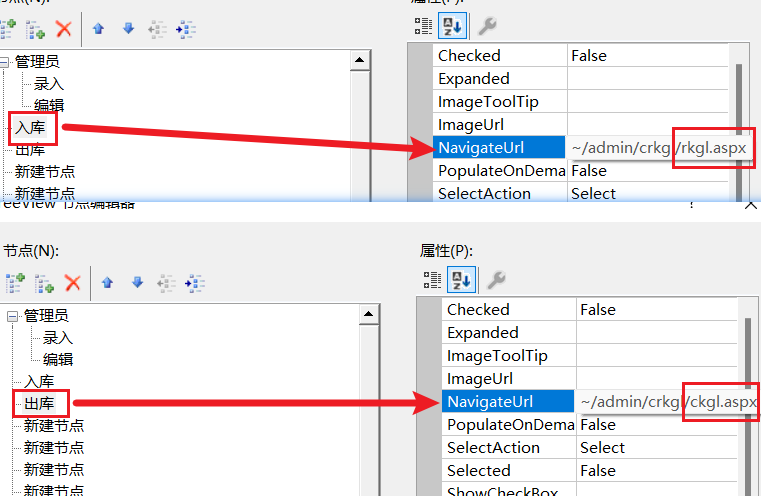
基于C#开发web网页管理系统模板流程-主界面管理员入库和出库功能完善
前言 紧接上篇->基于C#开发web网页管理系统模板流程-主界面管理员录入和编辑功能完善-CSDN博客 本篇将完善主界面的管理员入库和出库功能,同样的,管理员入库和出库的设计套路适用于动态表的录入和编辑 首先还是介绍一下本项目将要实现的功能 …...
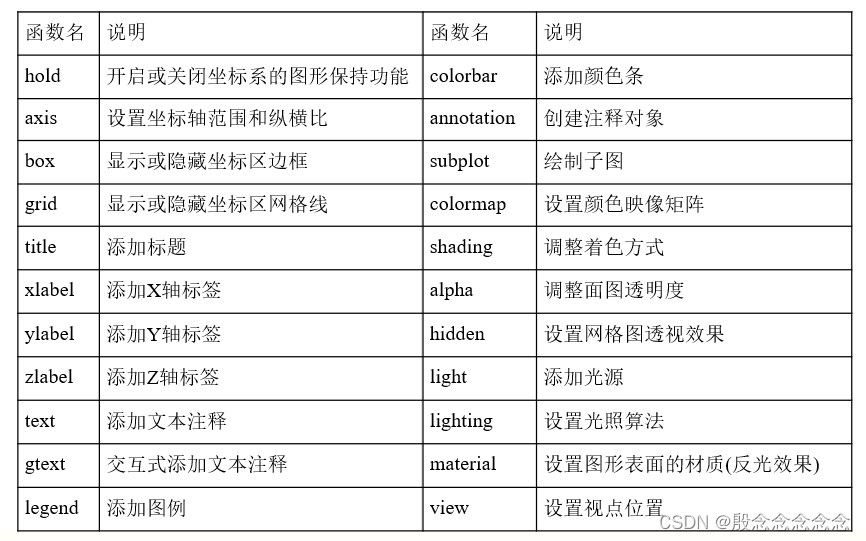
【MATLAB】概述1
非 ~ 注释 % 定义 >> 数组 赋值 赋值:>> x1 函数 数组 x[x1,x2] 行向量(,or ) x[x1;x2] 列向量 x. 转置等间隔向量 1-10 向量:>>xlinspace(1,10,10) 矩阵 矩阵:>>A[1,2,3;4,5,6;7,8,9] …...

容器中运行ip addr提示bash: ip: command not found【笔记】
容器中运行ip addr提示bash: ip: command not found 原因没有安装ip命令。 rootdocker-desktop:/# ip addr bash: ip: command not found rootdocker-desktop:/# apt-get install -y iproute2...

香橙派OrangePi AIpro,助力国产AIoT迈向新的台阶!
前言:很高兴受邀CSDN与OrangePi官方组织的测评活动,本次测评是一块基于AI边缘计算的香橙派开发板OrangePi AIpro。这是 香橙派 联合 华为昇腾 合作精心打造的新一代边缘AI计算产品,于2023年12月初发布,提供 8/20TOPS澎湃算力[1]&a…...
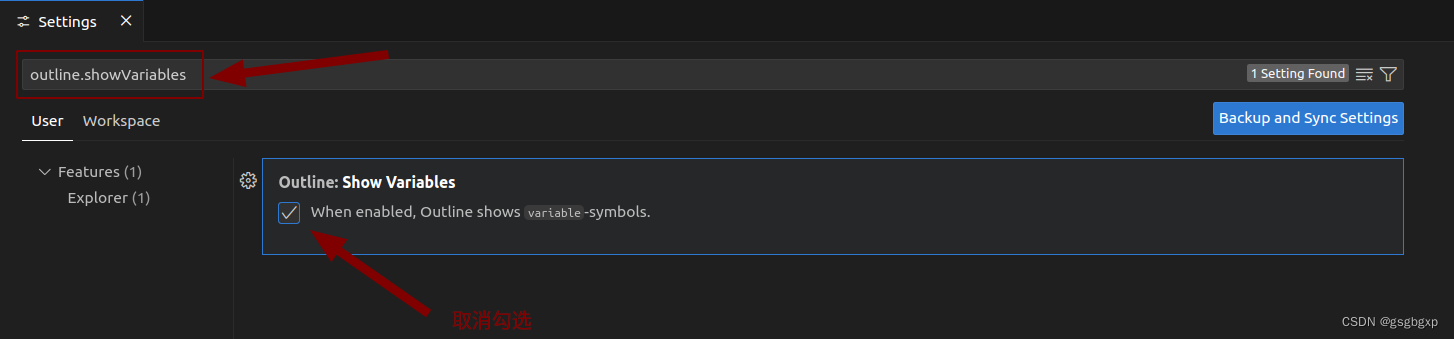
VSCode界面Outline只显示类名和函数名,隐藏变量名
参考链接 https://blog.csdn.net/Zjhao666/article/details/120523879https://blog.csdn.net/Williamcsj/article/details/122401996 VSCode中界面左下角的Outline能够方便快速跳转到文件的某个类或函数,但默认同时显示变量,导致找某个函数时很不方便。…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
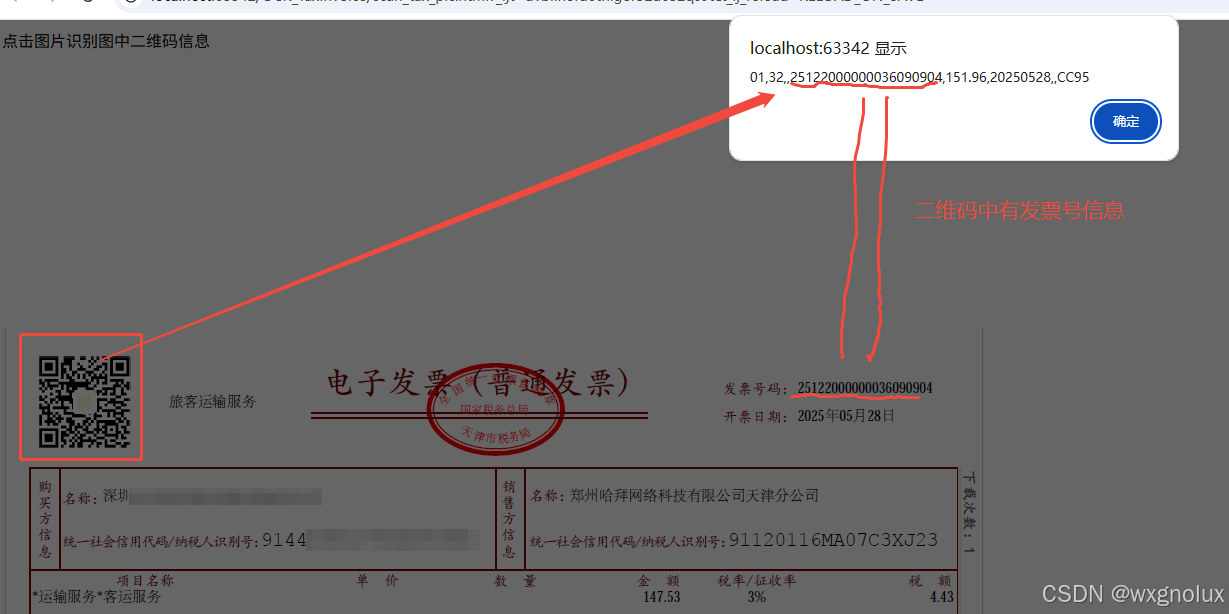
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
