当前位置： 首页 > news >正文

Echarts 在折线图的指定位置绘制一个图标展示

news 2026/2/8 0:53:37

文章目录

    • 需求
    • 分析

需求

在线段交汇处用一个六边形图标展示
在这里插入图片描述

分析

  • 可以使用 markPoint 和 symbol 属性来实现。这是一个更简单和更标准的方法来添加标记点
  • 在运行下述代码后，你将在浏览器中看到一个折线图，其中在 [3, 35] （即图表中第四个数据点 Thu 的 y 值为 35 的位置）处有一个六边形图标。你可以根据需要调整 coord 属性来设置六边形的位置，以及调整 symbolSize 和 itemStyle 来更改图标的大小和样式。
    demo展示：
<!DOCTYPE html>
<html style="height: 100%;

相关文章：

Echarts 在折线图的指定位置绘制一个图标展示

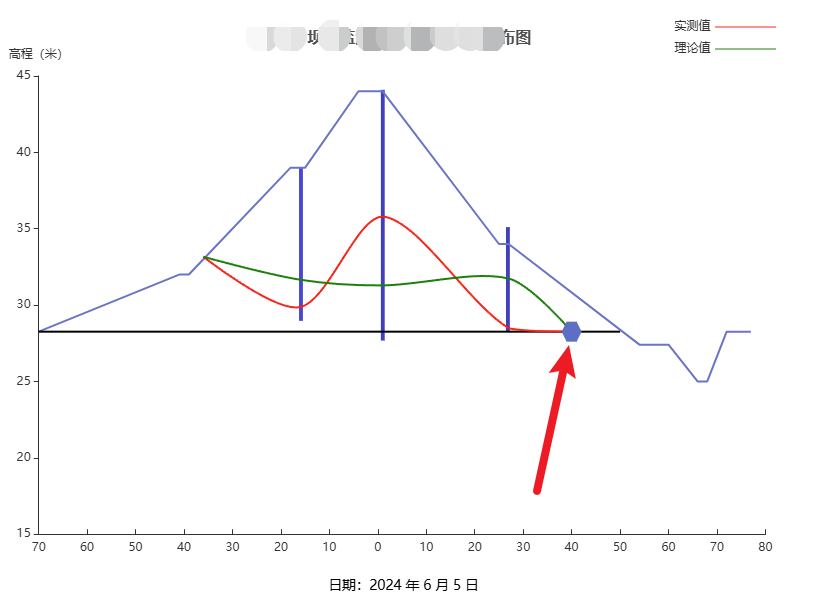
文章目录 需求分析需求 在线段交汇处用一个六边形图标展示 分析 可以使用 markPoint 和 symbol 属性来实现。这是一个更简单和更标准的方法来添加标记点在运行下述代码后，你将在浏览器中看到一个折线图，其中在 [3, 35] （即图表中第四个数据点 Thu 的 y 值为 35 的位置）处…...

编程日记 2024/6/5 13:35:39

适用于 Windows 的 8 大数据恢复软件

数据恢复软件可帮助您恢复因意外删除或由于某些技术故障&#xff08;如硬盘损坏等&#xff09;而丢失的数据。这些工具可帮助您从硬盘驱动器 (HDD) 中高效地恢复丢失的数据&#xff0c;因为这些工具不支持从 SSD 恢复数据。重要的是要了解&#xff0c;您删除的数据不会被系统永…...

编程日记 2024/6/5 13:33:36

HTTP基础

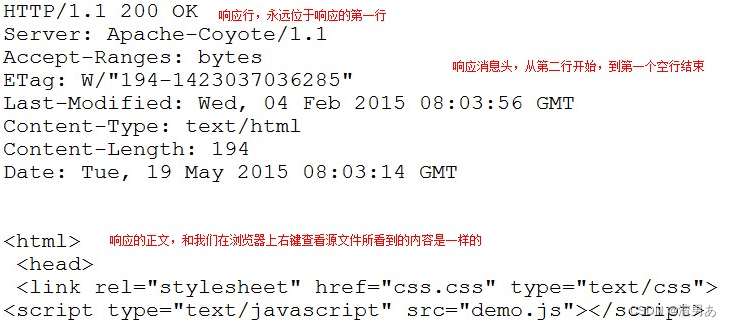
一、HTTP协议 1、HTTP协议概念 HTTP的全称是&#xff1a;Hyper Text Transfer Protocol&#xff0c;意为 超文本传输协议。它指的是服务器和客户端之间交互必须遵循的一问一答的规则。形容这个规则&#xff1a;问答机制、握手机制。 它规范了请求和响应内容的类型和格式, 是基于…...

编程日记 2024/6/5 13:32:34

深入了解Linux命令：visudo

深入了解Linux命令&#xff1a;visudo 在Linux系统中&#xff0c;sudo&#xff08;superuser do&#xff09;是一个允许用户以其他用户身份&#xff08;通常是超级用户或其他用户&#xff09;执行命令的程序。sudo的配置文件/etc/sudoers存储了哪些用户可以执行哪些命令的权限…...

编程日记 2024/6/5 13:29:31

十大排序 —— 希尔排序

十大排序 —— 希尔排序 什么是希尔排序插入排序希尔排序递归版本 我们今天来看另一个很有名的排序——希尔排序 什么是希尔排序 希尔排序&#xff08;Shell Sort&#xff09;是插入排序的一种更高效的改进版本&#xff0c;由Donald Shell于1959年提出。它通过比较相距一定间…...

编程日记 2024/6/5 13:26:29

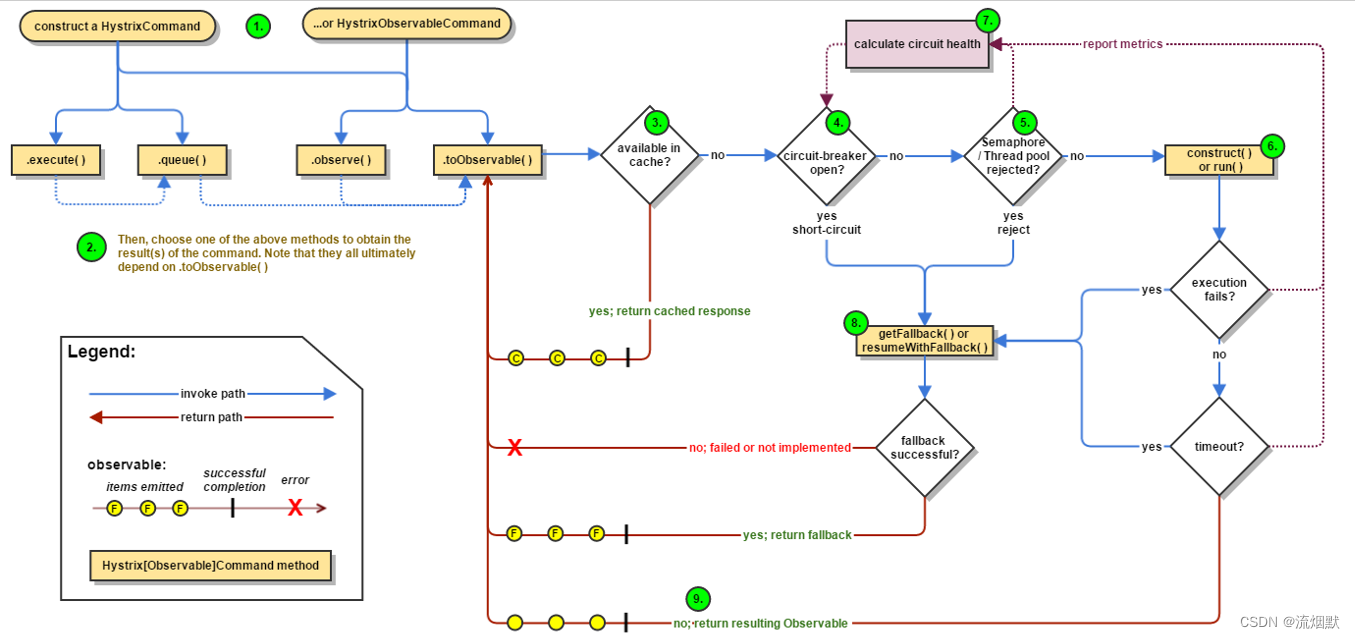
SpringCloud Hystrix服务熔断实例总结

SpringCloud Hystrix断路器-服务熔断与降级和HystrixDashboard SpringCloud Hystrix服务降级实例总结 本文采用版本为Hoxton.SR1系列&#xff0c;SpringBoot为2.2.2.RELEASE <dependency><groupId>org.springframework.cloud</groupId><artifactId>s…...

编程日记 2024/6/5 13:25:28

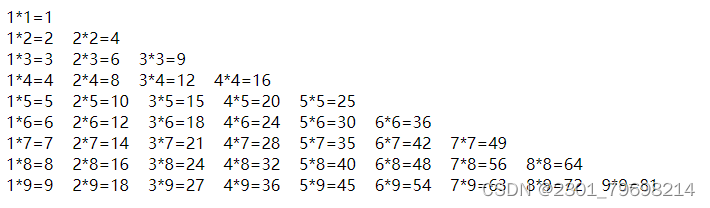
为什么没有输出九九乘法表？

下面的程序本来想输出九九乘法表到屏幕上&#xff0c;为什么没有输出呢&#xff1f;怎样修改&#xff1f; <!DOCTYPE html> <html> <head> <meta charset"utf-8" /> <title>我的HTML练习</title> …...

编程日记 2024/6/5 13:24:26

EasyRecovery5步轻松恢复电脑手机数据，EasyRecovery带你探索！

在当今的数字化时代&#xff0c;数据已经成为我们生活和工作中不可或缺的一部分。无论是个人照片、工作文件还是重要的商业信息&#xff0c;数据的安全存储和恢复都显得尤为重要。EasyRecovery作为一款广受欢迎的数据恢复软件&#xff0c;为用户提供了强大的数据恢复功能&#…...

编程日记 2024/6/5 13:20:22

904. 水果成篮

904. 水果成篮 原题链接&#xff1a;完成情况&#xff1a;解题思路&#xff1a;参考代码&#xff1a;_904水果成篮_滑动窗口 错误经验吸取 原题链接&#xff1a; 904. 水果成篮 https://leetcode.cn/problems/fruit-into-baskets/description/ 完成情况&#xff1a; 解题思…...

编程日记 2024/6/5 13:19:21

在618集中上新，蕉下、VVC们为何押注拼多多？

编辑&#xff5c;Ray 自前两年崛起的防晒产品&#xff0c;今年依旧热度不减。 头部品牌蕉下&#xff0c;2020年入驻拼多多&#xff0c;如今年销售额已过亿元。而自去年起重点押注拼多多的时尚防晒品牌VVC&#xff0c;很快销量翻番。这两家公司&#xff0c;不约而同在618之前上…...

编程日记 2024/6/5 13:18:20

Maximo Attachments配置

以下内容以 Windows 上 Maximo 为例&#xff0c;并假定设置 DOCLINKS 的根路径为 “C:\DOCLINKS”。 HTTP Server配置 修改C:\Program Files\IBM\HTTPServer\conf\httpd.conf文件 查找 “DocumentRoot” 并修改成如下配置 DocumentRoot "C:\DOCLINKS"查找 “<…...

编程日记 2024/6/5 13:17:19

一分钟了解香港的场外期权报价

香港的场外期权报价 在香港这个国际金融中心&#xff0c;场外期权交易是金融市场不可或缺的一部分。场外期权&#xff0c;作为一种非标准化的金融衍生品&#xff0c;为投资者提供了在特定时间以约定价格买入或卖出某种资产的机会。对于希望参与这一市场的投资者来说&#xff0…...

编程日记 2024/6/5 13:16:18

专业开放式耳机什么牌子更好？六大技巧教你不踩坑！

相信很多入坑的朋友再最开始挑选耳机的时候都会矛盾&#xff0c;现在市面上这么多耳机&#xff0c;我该怎么选择&#xff1f;其实对于开放式耳机&#xff0c;大家都没有一个明确的概念&#xff0c;可能会为了音质的一小点提升而耗费大量的资金&#xff0c;毕竟这是一个无底洞。…...

编程日记 2024/6/5 13:15:17

注意！！24软考系统集成有变化，第三版考试一定要看这个！

系统集成在今年年初改版之后&#xff0c;上半年的考试也取消了&#xff0c;留给大家充足的时间来学习新的教材和考纲。但11月也将是第三版考纲的第1次考试&#xff0c;重点到底有什么&#xff1f;今天带大家详细的了解一下最新版中项考试大纲。 一、考试说明 1.考试目标 通过…...

编程日记 2024/6/5 13:14:16

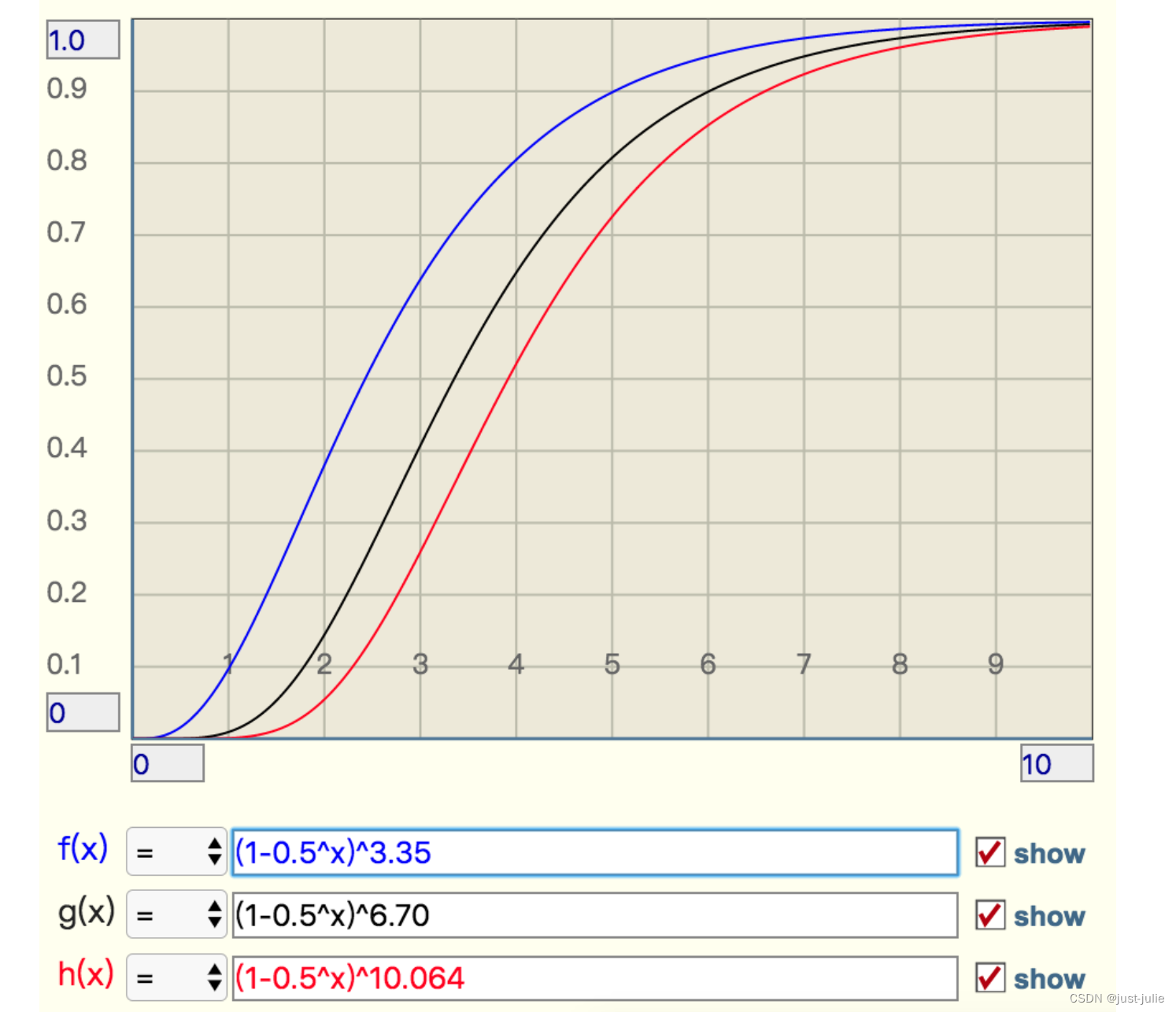
Redis数据结构HyperLogLog以及布隆过滤器

HyperLogLog 引言 在开始之前&#xff0c;先思考一个常见的业务问题&#xff1a;如果负责开发维护一个大型的网站&#xff0c;有一天老板找产品经理要网站每个网页每天的UV数据&#xff0c;然后来开发这个统计模块&#xff0c;需要如何实现&#xff1f; 如果统计PV非常好办&…...

编程日记 2024/6/5 13:13:15

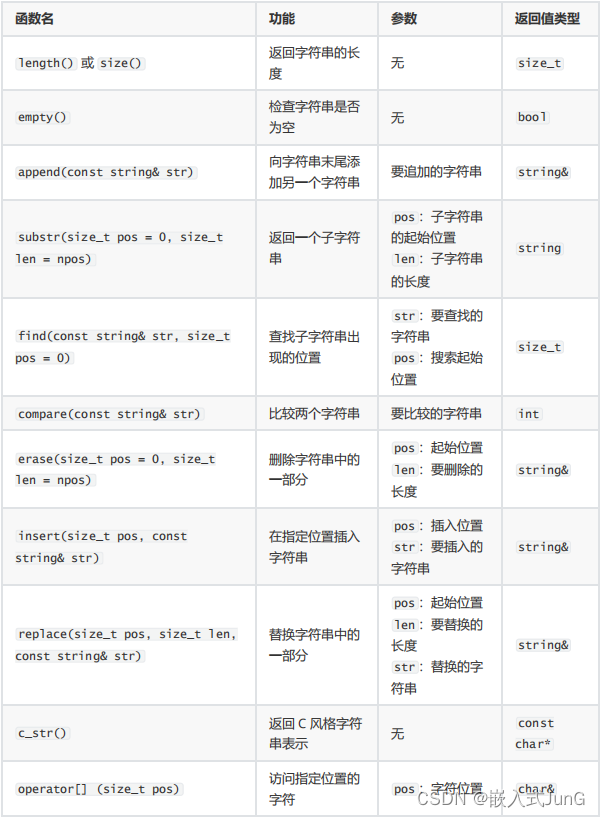
C++——从C语言快速入门

目录 一、数组 1、声明数组 2、初始化数组 3、访问数组元素 4、示例 5、注意事项 6、数组小练习 计算器支持加减乘除 数组找最大值 二、指针 三、字符串 string 类型 一、数组 在 C 中&#xff0c;数组是一种存储固定大小的相同类型元素的序列。数组的所有元素都存…...

编程日记 2024/6/5 13:09:09

thinkpad T440p ubuntu-slam软件安装记录

安装问题 1.ubuntu20.04安装后提示"x86/cpu:VMX(outside TXT) disabled by BIOS" 这是虚拟化被禁止了&#xff0c;到BIOS里去把Virtualization选项打开即可。 2.ACPI Error:Needed type[Reference],found [Integer] 等错误 link这篇博客中提到该问题&#xff0c;…...

编程日记 2024/6/5 13:08:08

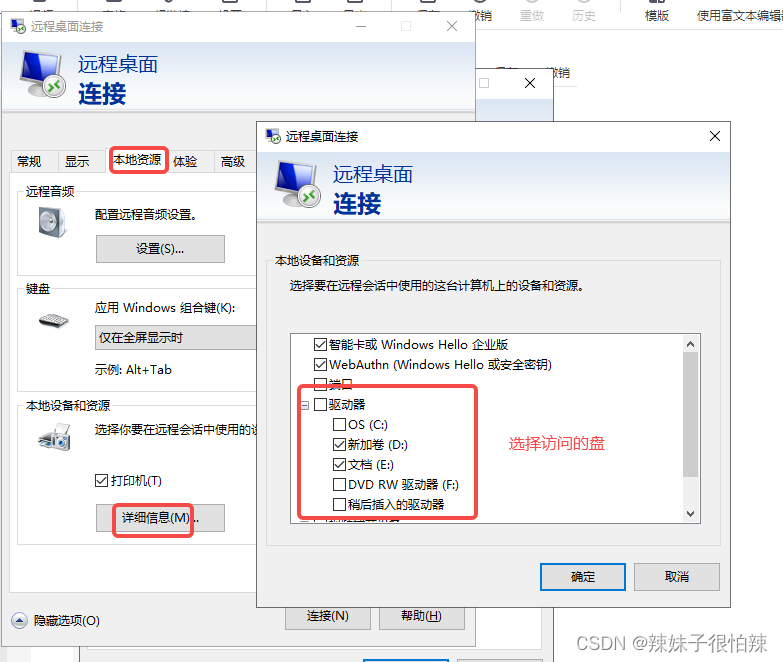
本地电脑访问windows server系统服务器 并传输文件

1、 mstsc 命令打开远程桌面连接。 2、填入登入的用户密码&#xff0c;在本地资源中设置需要共享的盘。登入成功后就可以在服务器与本地电脑互传文件了。...

编程日记 2024/6/5 13:05:05

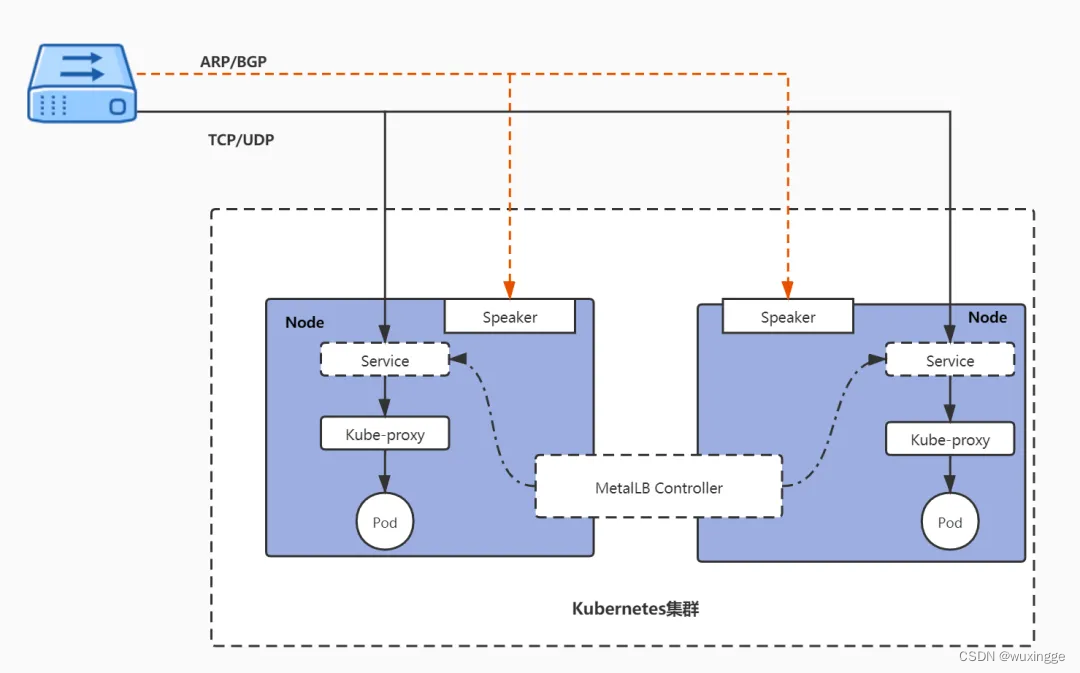
kubernetes负载均衡---MetalLB

https://github.com/metallb/metallb 参考 &#xff1a; https://mp.weixin.qq.com/s/MBOWfcTjFMmgJFWw-FIk0Q 自建的Kubernetes集群&#xff0c;默认情况下是不支持负载均衡的。当需要提供服务的外部访问时&#xff0c;可使用 Ingress、NodePort等方式。他们都存在一些问题 …...

编程日记 2024/6/5 12:59:59

Python面试宝典：Python中与设计模式相关的面试笔试题（1000加面试笔试题助你轻松捕获大厂Offer）

Python面试宝典：1000加python面试题助你轻松捕获大厂Offer【第二部分：Python高级特性：第二十二章：代码设计和设计模式：第二节：设计模式】 第二十二章：代码设计和设计模式第二节：设计模式创建型模式结构型模式行为型模式python中与设计模式相关的面试笔试题面试题1面试题…...

编程日记 2024/6/5 12:58:59

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank&#xff1f;由于时间太久&#xff0c;我真忘记了。搜搜发现&#xff0c;还真有人和我一样。见下面的链接&#xff1a;https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2026/2/5 0:36:44

java_网络服务相关_gateway_nacos_feign区别联系

1. spring-cloud-starter-gateway 作用&#xff1a;作为微服务架构的网关&#xff0c;统一入口&#xff0c;处理所有外部请求。 核心能力&#xff1a; 路由转发&#xff08;基于路径、服务名等&#xff09;过滤器&#xff08;鉴权、限流、日志、Header 处理&#xff09;支持负…...

编程新知 2025/11/28 2:51:33

逻辑回归：给不确定性划界的分类大师

想象你是一名医生。面对患者的检查报告&#xff08;肿瘤大小、血液指标&#xff09;&#xff0c;你需要做出一个**决定性判断**&#xff1a;恶性还是良性&#xff1f;这种“非黑即白”的抉择&#xff0c;正是**逻辑回归&#xff08;Logistic Regression&#xff09;** 的战场&a…...

编程新知 2025/10/27 21:25:04

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括&#xff1a;采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中&#xff0c;设置任务排序规则尤其重要&#xff0c;因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明&#xff1a;server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2026/1/23 4:15:03

测试markdown--肇兴

day1&#xff1a; 1、去程&#xff1a;7:04 --11:32高铁 高铁右转上售票大厅2楼&#xff0c;穿过候车厅下一楼&#xff0c;上大巴车 &#xffe5;10/人 **2、到达&#xff1a;**12点多到达寨子&#xff0c;买门票&#xff0c;美团/抖音&#xff1a;&#xffe5;78人 3、中饭&a…...

编程新知 2025/12/14 11:45:02

c++ 面试题(1)-----深度优先搜索（DFS）实现

操作系统&#xff1a;ubuntu22.04 IDE:Visual Studio Code 编程语言&#xff1a;C11 题目描述 地上有一个 m 行 n 列的方格&#xff0c;从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子&#xff0c;但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

编程新知 2026/1/10 10:16:16

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言&#xff1a; 在人工智能快速发展的浪潮中&#xff0c;快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型&#xff08;LLM&#xff09;。该模型代表着该领域的重大突破&#xff0c;通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2025/10/5 19:58:27

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2026/2/1 5:24:17