Day43 代码随想录打卡|二叉树篇---左叶子之和
题目(leecode T404):
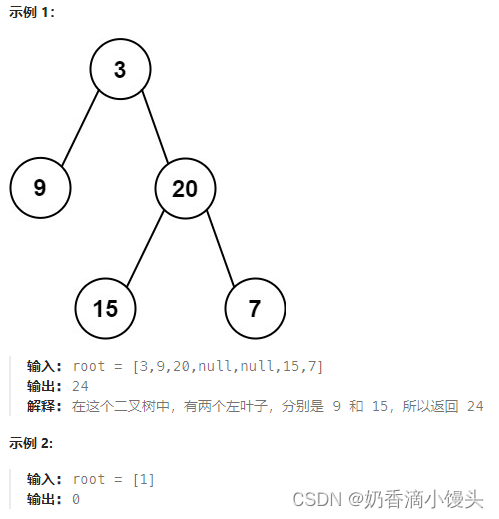
给定二叉树的根节点 root ,返回所有左叶子之和。
方法:
迭代法:计算所有的左叶子节点,那我们就必然要找到所有的左叶子节点。那么怎么找呢?如何针对cur->left == NULL&&cur->right ==NULL的话只能判断当前节点是叶子节点,而无法判断出具体是左还是右。因此我们需要从左叶子节点的父节点进行判断,即cur->left != NULL&&cur->left == NULL&&cur->right ==NULL,这样的节点的左孩子结点就是一个左叶子节点。我们这样就确定好了找到左叶子节点的判断逻辑。下面分析迭代的三部曲。
1:确定传入的参数和返回值,传入的参数就是要处理的树节点,返回值是左叶子节点的数值之和,因此需要为int,进行迭代累加得到的就是做叶子节点的和。
2:确定终止条件,当我们遍历到了空节点时,肯定是没有左孩子结点了,就需要终止。
3:确定单层的处理逻辑,当我们找到了左叶子节点时,就记录左叶子节点的值,同时递归根节点的左右子树,最后将两值相加即可得到该树的左叶子节点之和。
题解:
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if(root == NULL) return 0; //终止逻辑int leftValue = sumOfLeftLeaves(root->left); //递归左子树if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){ //找到左叶子节点就记录其数值leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right); //递归右子树int sum = leftValue + rightValue;return sum;}
};相关文章:

Day43 代码随想录打卡|二叉树篇---左叶子之和
题目(leecode T404): 给定二叉树的根节点 root ,返回所有左叶子之和。 方法: 迭代法:计算所有的左叶子节点,那我们就必然要找到所有的左叶子节点。那么怎么找呢?如何针对cur->l…...

微信小程序动画
微信小程序动画属性:提升用户体验的利器 引言 随着移动互联网技术的快速发展,微信小程序已经成为开发者和用户的热门选择。其轻便、快捷、即用即走的特点使得它在各种场景中都有广泛的应用。而动画作为一种重要的视觉元素,在增强用户体验方…...

js, ellipsis属性, 超出宽度自动省略... , 并且显示2行
overflow:hidden; display:-webkit-box; -webkit-line-clamp:2; -webkit-box-orient:vertical; text-overflow:ellipsis;...

ucharts自定义添加tooltip悬浮框显示项内容且换行
欢迎点击领取 -《前端开发面试题进阶秘籍》:前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 一、需求描述分析 1、小程序上实现图表的绘制,多条线路,不同颜色,悬浮框对应内容不同数据进行处理 2…...

Mongo 地理位置查询:海量密集点转换成聚合信息
通俗来说:将地图上的海量密集点通过网格分割的方式实现聚合; 需求:用mongo实现设备地理位置聚合查询 :多边形,矩形查询; 背景:上万设备数据量 目的:分享Mongo地理位置查询,以及文…...

bpmn+vue 中文文档
1.初始化项目 <script> import BpmnModeler from bpmn-js/lib/Modeler import { xmlStr } from /mock/xmlStr export default {mounted () {this.init()},methods: {init () {// 获取到属性ref为“canvas”的dom节点const canvas this.$refs.canvas// 建模const custom…...

React Router v5 和 v6 中,路由对象声明方式有什么区别?
一、在React Router 6.x开始,路由对象的声明需要引用RouteObject。 import { RouteObject } from react-router-dom;const routes: RouteObject[] [{path: /,element: <Home />},{path: /about,element: <About />},// ... ];二、一些老项目使用的是R…...
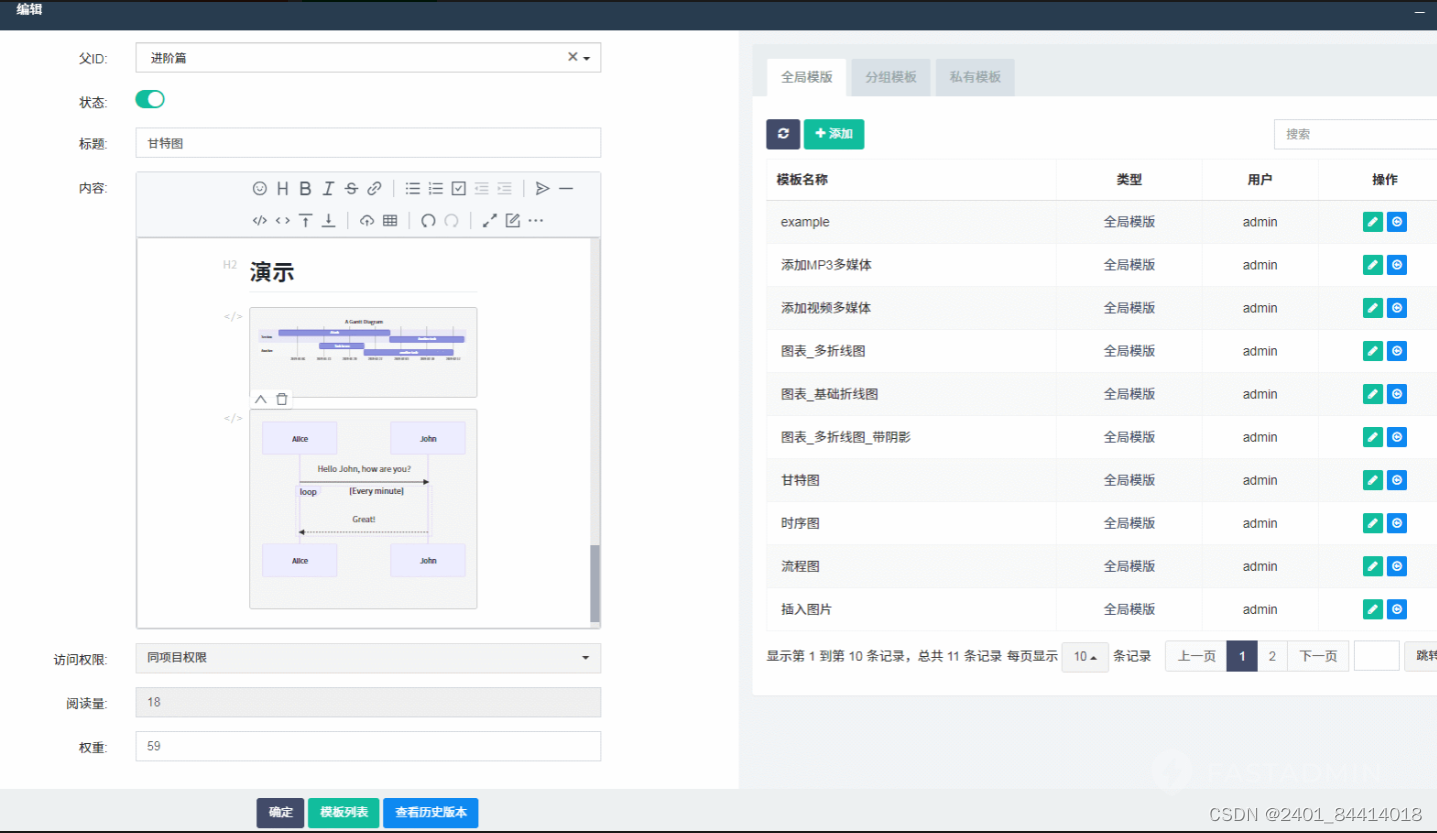
【全开源】知识库文档系统(ThinkPHP+FastAdmin)
📚知识库文档系统:解锁知识的无限可能 一款基于ThinkPHPFastAdmin开发的知识库文档系统,可用于企业工作流程的文档管理,结构化记录沉淀高价值信息,形成完整的知识体系,能够轻松提升知识的流转和传播效率&a…...

Python赋能自然语言处理,解锁通往AI的钥匙
NLTK(Natural Language Toolkit)是一个用于 Python 的自然语言处理库,提供了丰富的工具和资源,帮助处理、分析和理解人类语言数据.它广泛应用于学术研究、教育和商业应用中. 安装 #首先要安装 NLTK:pip install nltk安装完成后,还需要下载…...

Ktor库的高级用法:代理服务器与JSON处理
在现代网络编程中,Ktor是一个高性能且易于使用的框架,它提供了对异步编程、WebSockets、HTTP客户端和服务器等特性的原生支持。Ktor是使用Kotlin语言编写的,充分利用了Kotlin的协程特性来简化异步编程。本文将深入探讨Ktor库的高级用法&#…...
VS2017配置OpenCV4.5.1
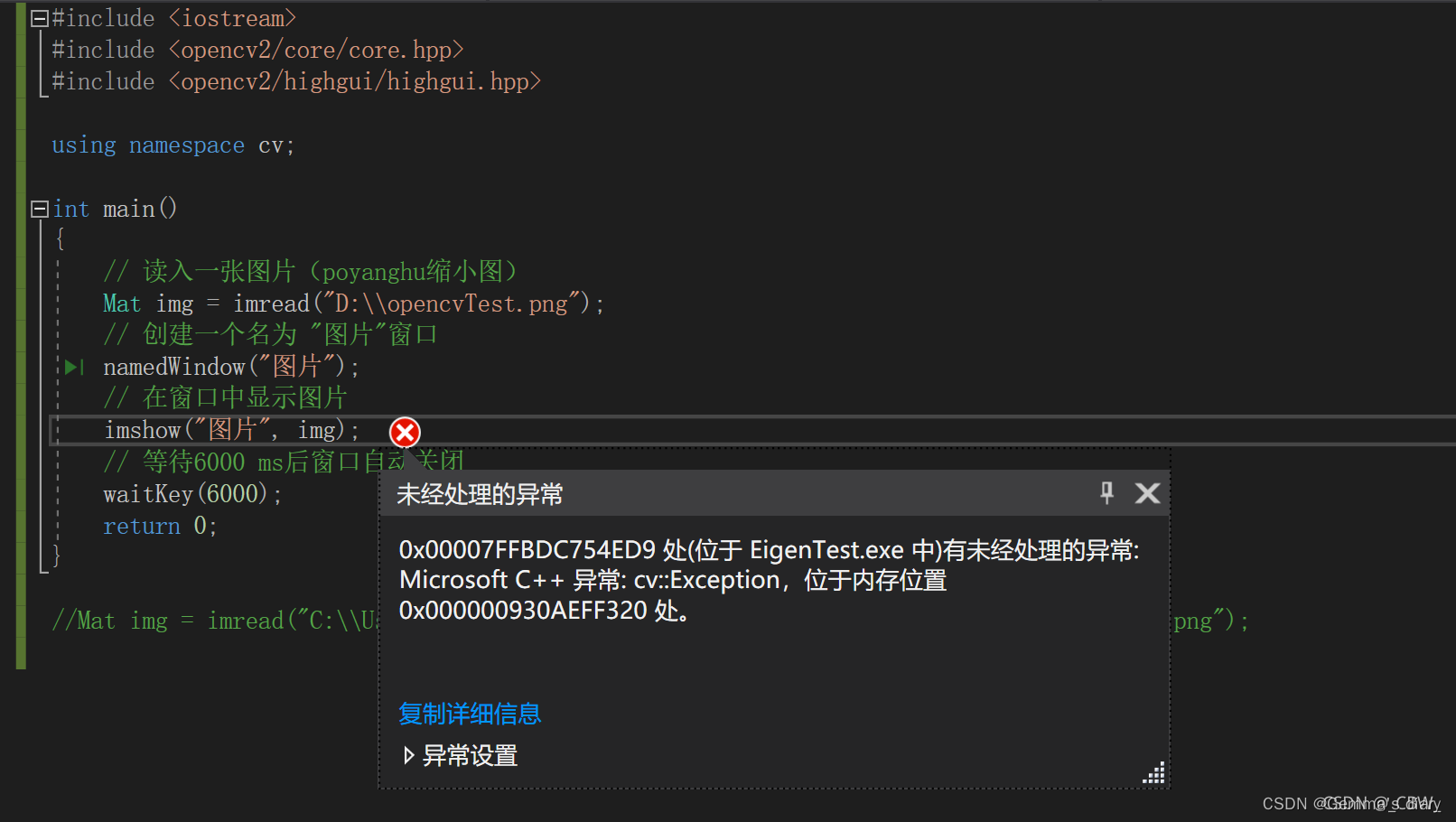
VS2017配置OpenCV 一、下载OpenCV二、配置OpenCV的电脑环境变量三、配置visual Studio添加路径复制文件到C盘 四、如何使用注意运行时选择Debug x64 五、报错:VSOpencv出现:xxx处有未经处理的异常: Microsoft C 异常: cv::Exception,位于内存…...
phpstudy配置的站点不能访问了
无法打开站点 打开网站的时候出现如下 没有人为主动去更改配置项,今天就不能正常访问了 检查了一遍配置,发现并无大碍,那就重新配置一遍看看 配置phpstudy 1、新建网站 2、选择项目入口文件夹 3、配置伪静态 4. 确认保存 在我的电脑 C:\…...
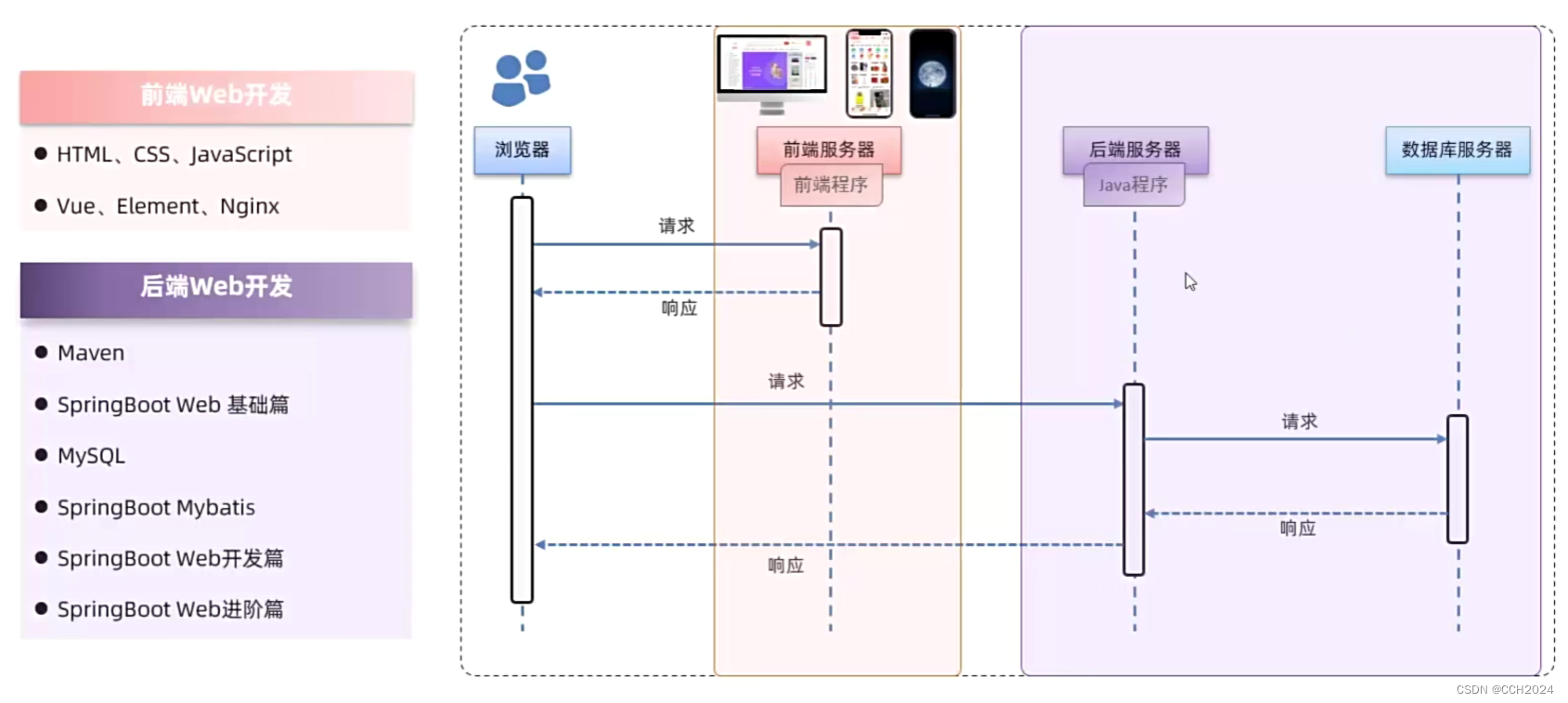
Java Web学习笔记2——Web开发介绍
什么是Web? Web:全球广域网,也称为万维网(WWW World Wide Web),能够通过浏览器访问的网站。 1)淘宝、京东、唯品会等电商系统; 2)CRM、OA、ERP企业管理系统࿱…...
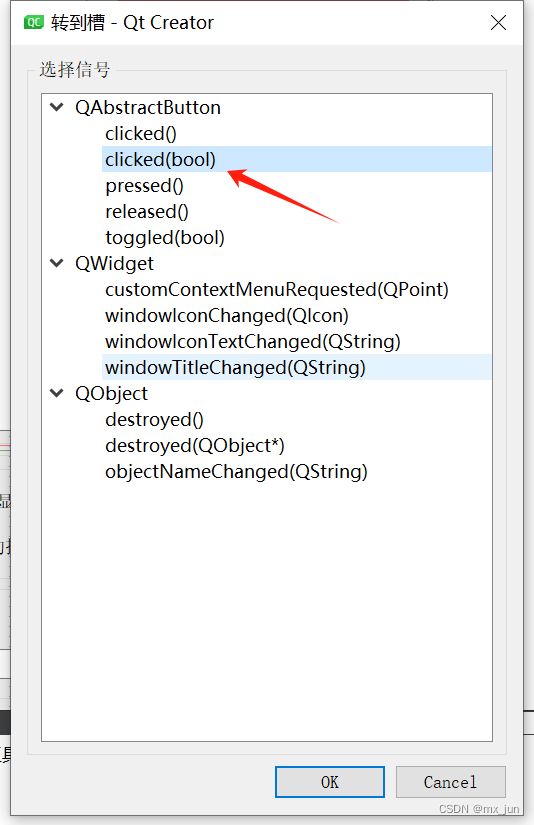
从零开始实现自己的串口调试助手(3) - 显示底部收发,优化串口打开/关闭
注意: 1. 我们要实现自发自收,要将tx,rx连起来 2.发送的 不能是中文符号,因为这可能导致,读取到的是英文符号 --> 导致接收到的size 和发送的size 大小不一致 3.注意同时定义两个槽函数的时候两个槽函数都会被调用,…...

更改Web网站设计——css和css框架
虽然使用HTML可以定义文章的结构,但是其中不包含设计相关的信息。此时CSS就派上用场,可以用它对HTML文章指定设计样式。由于可以决定Web网页的外观风格,因此,它有时也被称为格式表。 如果使用CSS设置背景色,文…...

持续监控和优化的简单介绍
DevOps 监控提供了有关生产环境状况的全面且最新的信息,以及有关其服务、基础设施和应用程序的详细信息。通过从日志和指标中收集数据,您可以在软件开发生命周期的每个步骤中监控合规性和性能。 监控不仅仅针对生产问题,它涵盖了规划、开发、…...
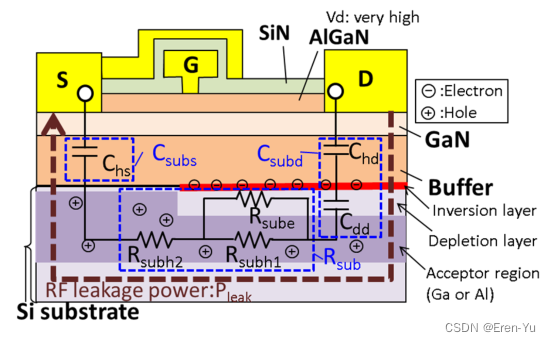
针对硅基氮化镓高电子迁移率晶体管(GaN-HEMT)的准物理等效电路模型,包含基板中射频漏电流的温度依赖性
来源:Quasi-Physical Equivalent Circuit Model of RF Leakage Current in Substrate Including Temperature Dependence for GaN-HEMT on Si(TMTT 23年) 摘要 该文章提出了一种针对硅基氮化镓高电子迁移率晶体管(GaN-HEMT&…...

基于websocket与node搭建简易聊天室
一、前言 上一篇文章介绍了websocket的详细用法与工具类的封装,本篇就基于websocket搭建一个简易实时的聊天室。 在本篇开始之前也可以去回顾一下websocket详细用法:WebSocket详解与封装工具类 二、基于node搭建后台websocket服务 首先确认本机电脑中…...

DevOps全面综述:从概念到实践
一、背景与概述 1.1 DevOps的起源与发展 DevOps(Development and Operations的缩写)是软件工程领域中的一种文化和实践方法,旨在促进开发团队与运维团队之间的协作,从而实现更高效、更可靠的软件交付。DevOps起源于敏捷软件开发方…...
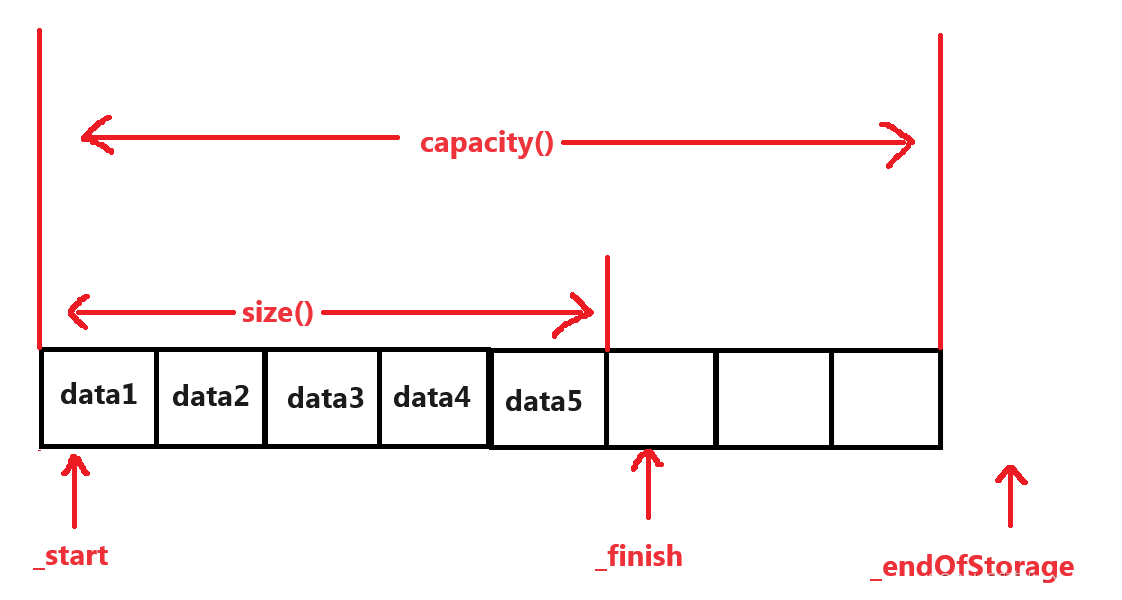
[C++]vector的模拟实现
下面是简单的实现vector的功能,没有涉及使用内存池等复杂算法来提高效率。 一、vector的概述 (一)、抽象数据类型定义 容器:向量(vector)vector是表示大小可以变化的数组的序列容器。像数组一样…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
