数据结构的归并排序(c语言版)

一.归并排序的基本概念
1.基本概念
归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下:
- 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。
- 然后将这些子数组两两归并,得到有序的子数组。
- 不断重复第二步,直到最终得到有序的整个数组。
2.核心思想
归并排序的核心是"分而治之"的思想。通过不断地将数组拆分成更小的子数组,直至子数组只有一个元素,然后再将这些有序的子数组合并起来,最终得到一个有序的数组。
与简单的冒泡排序或选择排序相比,归并排序的时间复杂度为O(nlogn),这使它能够高效地处理大规模的数据集。虽然它需要O(n)的额外空间来存储中间结果,但其优秀的时间复杂度使其成为处理大数据量排序问题的首选算法之一。
总的来说,归并排序是一种强大而高效的排序算法,它体现了分治策略在算法设计中的重要应用。如果您有任何其他问题,欢迎随时向我咨询。
3.优点
优点:
-
时间复杂度稳定:归并排序的时间复杂度为O(nlogn),不管输入数据的初始状态如何,时间复杂度都是稳定的。这使它能够高效处理大规模数据。
-
稳定排序:归并排序是一种稳定的排序算法,也就是说,当两个相等的元素出现时,它们在输出序列中的相对顺序与输入序列中的相对顺序一致。这对某些应用场景很重要。
-
并行计算友好:归并排序的"分而治之"特性使得它很容易并行化,在多核处理器上可以获得很好的性能提升。
4.缺点
缺点:
-
需要额外空间:归并排序需要额外的内存空间来存储中间结果,空间复杂度为O(n)。这可能成为一个瓶颈,尤其是在内存受限的环境中。
-
数据交换频繁:归并排序需要频繁地将数据从输入数组复制到临时数组,这在某些情况下可能会降低性能。
-
无法就地排序:归并排序无法在原数组上就地排序,需要使用额外的空间。这对于某些内存受限的场景可能是个问题。
二.归并排序的功能
归并排序的基本功能就是对一组数据进行排序。具体来说,它可以实现以下几个功能:
-
将无序的数组或列表排序为有序的数组或列表。归并排序可以将任意大小的输入集合有效地排序,包括大型数据集。
-
保持数据的相对位置关系。如果输入数据中存在相等的元素,归并排序会保留它们原有的相对顺序,这在某些应用场景中很重要。
-
支持并行计算。由于归并排序的"分而治之"特性,它非常适合在多核处理器上并行执行,从而获得大幅的性能提升。
-
可以用于外部排序。当数据量太大无法一次性装入内存时,可以采用外部排序的方式,先将数据划分成多个小块,然后使用归并排序分别对这些小块进行排序,最后合并这些有序块。
-
可以作为其他算法的子过程。归并排序常被用作其他算法的核心步骤,比如快速排序、外部排序等。
归并排序是一种通用且高效的排序算法,它在各种规模和类型的数据排序中都有重要应用。它的功能十分强大,能够满足绝大多数排序需求。
三.归并排序的代码实现
1.合并两个有序数组
- 定义三个索引变量
i,j,k,分别用来遍历左数组、右数组和目标数组。 - 使用
while循环比较左右数组当前元素的大小,将较小的元素依次添加到目标数组中。 - 当左数组或右数组中还有剩余元素时,将它们依次添加到目标数组的末尾。
// 合并两个有序数组
void merge(int arr[], int left[], int left_size, int right[], int right_size, int size) {int i = 0, j = 0, k = 0;while (i < left_size && j < right_size) {if (left[i] <= right[j]) {arr[k++] = left[i++];} else {arr[k++] = right[j++];}}while (i < left_size) {arr[k++] = left[i++];}while (j < right_size) {arr[k++] = right[j++];}
}2.递归实现
-
首先,它检查数组大小是否小于等于 1,如果是,则直接返回,因为单个元素已经是有序的了。
-
接下来,它将数组分为两个子数组:左子数组
left和右子数组right。计算中点mid作为分割点,将原数组arr分为左右两部分。 -
然后,它将原数组
arr的元素复制到左右两个临时数组left和right中。 -
递归地对左右两个子数组分别调用
merge_sort函数,对它们进行排序。 -
最后,它调用
merge函数,将已经排序的左右子数组合并回原数组arr。
// 递归实现归并排序
void merge_sort(int arr[], int size) {
if (size <= 1) {
return;
}
int mid = size / 2;
int left[mid];
int right[size - mid];
for (int i = 0; i < mid; i++) {
left[i] = arr[i];
}
for (int i = mid; i < size; i++) {
right[i - mid] = arr[i];
}
merge_sort(left, mid);
merge_sort(right, size - mid);
merge(arr, left, mid, right, size - mid);
}3.非递归实现
-
首先,它申请了一个临时数组
temp,用来存储合并后的有序子数组。这是非递归实现所需要的额外空间。 -
然后,它使用一个外层循环来控制子数组的宽度
width。初始值为 1,每次翻倍,直到width大于等于数组大小size。 -
内层循环遍历数组,每次处理长度为
2 * width的两个相邻子数组。 -
对于每个子数组对,它计算左子数组的长度
left_size为width,右子数组的长度right_size可能会小于width(当剩余元素不足width时)。 -
然后调用
merge函数,将左右两个有序子数组合并为一个有序子数组,存储在原数组arr中。 -
最后,释放临时数组
temp占用的动态内存。
// 非递归实现归并排序
void iterative_merge_sort(int arr[], int size) {int *temp = (int *)malloc(size * sizeof(int));if (!temp) {printf("Memory allocation failed.\n");return;}for (int width = 1; width < size; width *= 2) {for (int i = 0; i < size; i += 2 * width) {int left_size = width;int right_size = (i + 2 * width < size) ? width : size - i - width;merge(arr + i, arr + i, left_size, arr + i + width, right_size, size);}}free(temp);
}四.归并排序的源代码
1.递归
#include <stdio.h>
#include <stdlib.h>// 合并两个有序数组
void merge(int arr[], int left[], int left_size, int right[], int right_size) {int i = 0, j = 0, k = 0;while (i < left_size && j < right_size) {if (left[i] <= right[j]) {arr[k++] = left[i++];} else {arr[k++] = right[j++];}}while (i < left_size) {arr[k++] = left[i++];}while (j < right_size) {arr[k++] = right[j++];}
}// 递归实现归并排序
void merge_sort(int arr[], int size) {if (size <= 1) {return;}int mid = size / 2;int left[mid];int right[size - mid];for (int i = 0; i < mid; i++) {left[i] = arr[i];}for (int i = mid; i < size; i++) {right[i - mid] = arr[i];}merge_sort(left, mid);merge_sort(right, size - mid);merge(arr, left, mid, right, size - mid);
}int main() {int arr[] = {5, 2, 4, 6, 1, 3, 2, 6};int size = sizeof(arr) / sizeof(arr[0]);merge_sort(arr, size);for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}2.非递归
#include <stdio.h>
#include <stdlib.h>// 合并两个有序数组
void merge(int arr[], int left[], int left_size, int right[], int right_size, int size) {int i = 0, j = 0, k = 0;while (i < left_size && j < right_size) {if (left[i] <= right[j]) {arr[k++] = left[i++];} else {arr[k++] = right[j++];}}while (i < left_size) {arr[k++] = left[i++];}while (j < right_size) {arr[k++] = right[j++];}
}// 非递归实现归并排序
void iterative_merge_sort(int arr[], int size) {int *temp = (int *)malloc(size * sizeof(int));if (!temp) {printf("Memory allocation failed.\n");return;}for (int width = 1; width < size; width *= 2) {for (int i = 0; i < size; i += 2 * width) {int left_size = width;int right_size = (i + 2 * width < size) ? width : size - i - width;merge(arr + i, arr + i, left_size, arr + i + width, right_size, size);}}free(temp);
}int main() {int arr[] = {5, 2, 4, 6, 1, 3, 2, 6};int size = sizeof(arr) / sizeof(arr[0]);iterative_merge_sort(arr, size);for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}相关文章:

数据结构的归并排序(c语言版)
一.归并排序的基本概念 1.基本概念 归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下: 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。然后将这些子数组两两归并,得到有序的子数组。不断重复第二步,直到最终得到有序的整个数组。 2.核心…...

ubuntu使用Docker笔记
一、参考资料 1、B站视频 尚硅谷Docker实战教程 2、有心人整理的笔记 Docker笔记(周阳版) 3、菜鸟教程 Docker 教程 以下是本人的折腾实践。 二、Docker的安装 2.1、使用清华源安装docker,清华源官方教程。 本人是在ubuntu20.04下安装的…...

PHP编程入门:揭开Web开发的神秘面纱
PHP编程入门:揭开Web开发的神秘面纱 在数字化时代,PHP作为一种广泛使用的服务器端脚本语言,为Web开发领域注入了强大的活力。无论你是编程新手还是有一定经验的开发者,掌握PHP编程都将为你开启一扇通往Web开发新世界的大门。接下…...
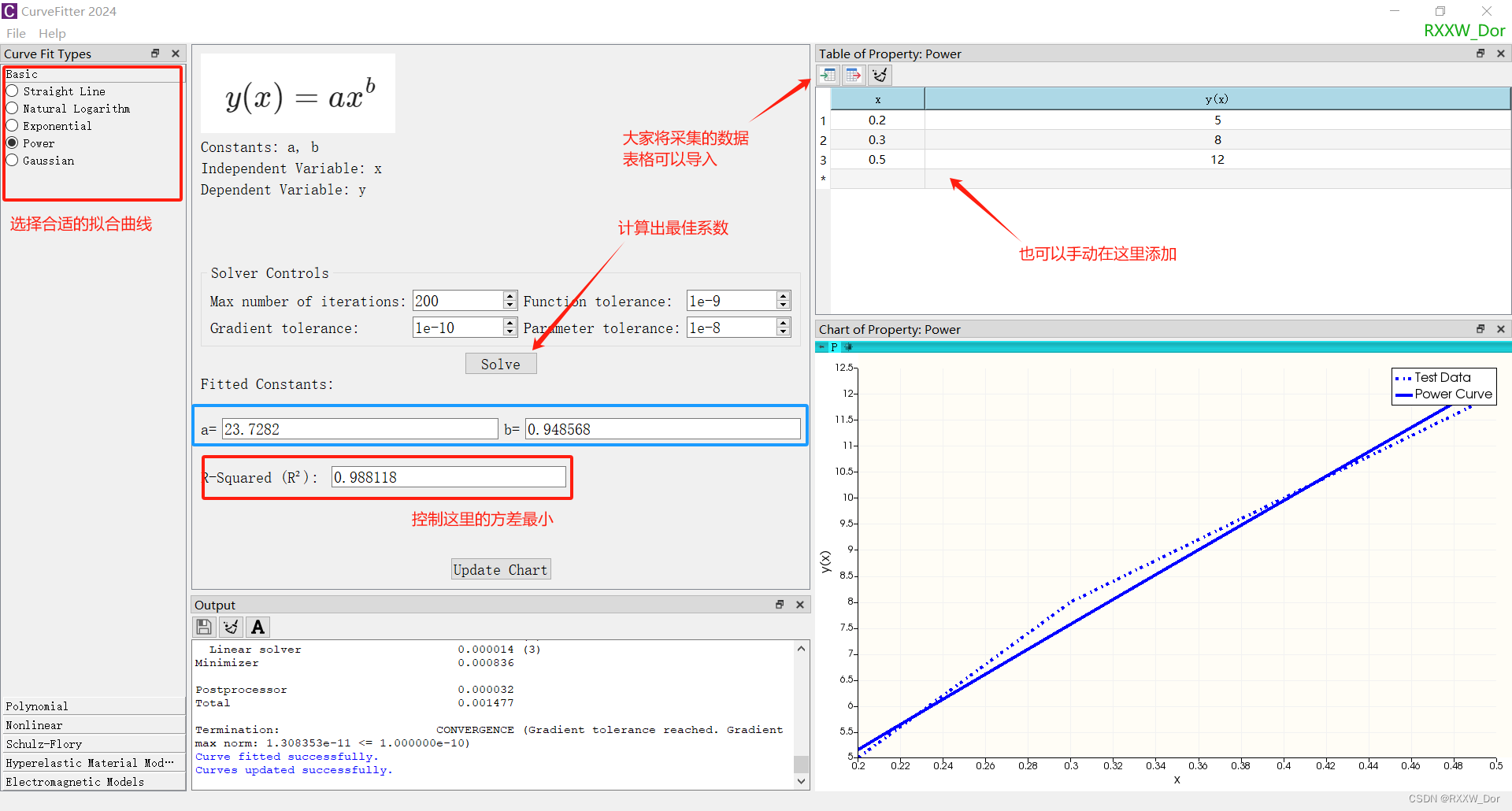
曲线拟合工具软件(免费)
曲线拟合是数据处理中经常用到的数值方法,本质是使用某一个模型(方程或者方程组)将一系列离散的数据拟合成平滑的曲线或者曲面,数值求解出对应的函数参数,大家可以利用MATLAB的曲线拟合工具箱也可以使用第三方的拟合软件,今天我们介绍Welsim免费的曲线拟合软件 1、MATLA…...
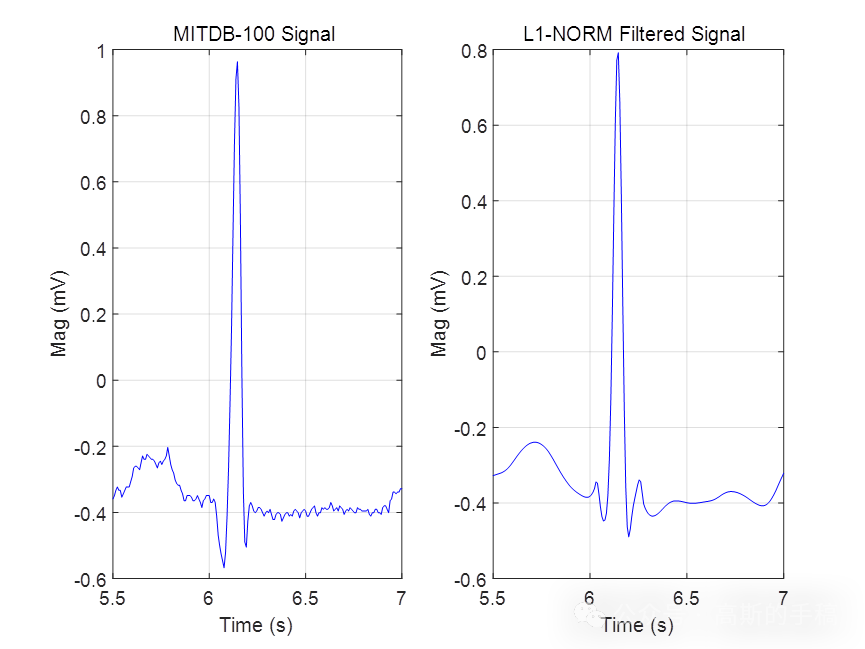
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一…...
)
Bitbucket的原理及应用详解(一)
本系列文章简介: 在数字化和全球化的今天,软件开发和项目管理已经成为企业成功的关键因素之一。随着团队规模的扩大和项目的复杂化,如何高效地协同开发、管理代码和确保代码质量成为了开发者和管理者面临的重要挑战。Bitbucket作为一款功能强…...

企业级win10电脑下同时存在Python3.11.7Python3.6.6,其中Python3.6.6是后装的【过程与踩坑复盘】
背景: 需要迁移原始服务器的上的Python3.6.6+Flask项目到一个新服务器上, 新服务器上本身存在一个Python3.11.7, 所以这涉及到了一个电脑需要装多个Python版本的问题 过程: 1-确定新电脑版本【比如是32还是64位】 前面开发人员存留了两个包,是python-3.6.6.exe和pytho…...

泛微开发修炼之旅--03常用数据表结构讲解
文章链接:泛微开发修炼之旅--03常用数据表结构讲解...

MySQL8找不到my.ini配置文件以及报sql_mode=only_full_group_by解决方案
一、找不到my.ini配置文件 MySQL 8 安装或启动过程中,如果系统找不到my.ini文件,通常意味着 MySQL服务器没有找到其配置文件。在Windows系统上,MySQL 8 预期使用my.ini作为配置文件,而不是在某些情况下用到的my.cnf文件。 通过 …...

Android 13 亮度调节代码分析
frameworks\base\packages\SystemUI\res\layout\quick_settings_brightness_dialog.xml 进度条控件 <com.android.systemui.settings.brightness.BrightnessSliderViewxmlns:android"http://schemas.android.com/apk/res/android"android:id"id/brightness…...
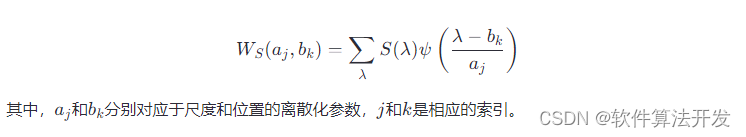
基于小波变换和峰值搜索的光谱检测matlab仿真,带GUI界面
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于小波变换和峰值搜索的光谱检测matlab仿真,带GUI界面.对光谱数据的成分进行提取,分析CO2,SO2,CO以及CH4四种成分比例。 2.…...

【初识Objective-C】
Objective-C学习 什么是OCOC的特性OC跑的第一个程序helloworld OC的一些基础知识标识符OC关键字数据类型字符型c字符串为什么NSString类型定义时前面要加和普通的c对象有什么区别 一些基础知识if语句switch语句三种循坏语句for循环:用于固定次数的循环while循环&…...
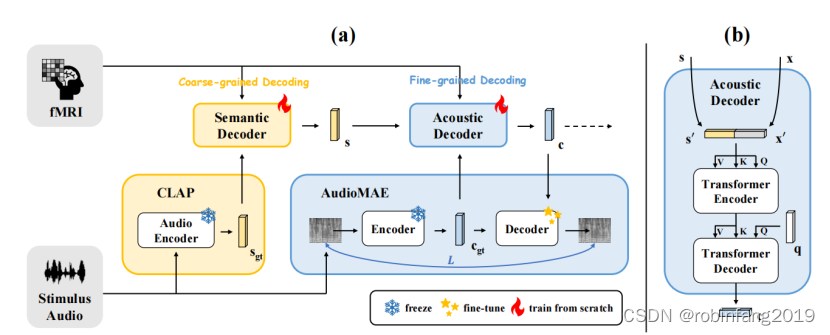
从功能性磁共振成像(fMRI)数据重建音频
听觉是人类最重要的感官之一,它负责接收外部的听觉刺激,并将这些信息传递给大脑进行处理和理解。研究人员正致力于从神经科学和计算机科学两个领域探索人脑的听觉感知机制。一个关键目标是从人脑中解码神经信息,并重建原始的刺激。常见的大脑…...

前端Vue小兔鲜儿电商项目实战Day04
一、二级分类 - 整体认识和路由配置 1. 配置二级路由 ①准备组件模板 - src/views/SubCategory/index.vue <script setup></script><template><div class"container"><!-- 面包屑 --><div class"bread-container">…...

TypeScript的简单总结
TypeScript 深度总结 引言 TypeScript,作为JavaScript的一个强类型超集,由Microsoft在2012年推出并维护至今,它不仅继承了JavaScript的所有特性,还引入了静态类型系统和其他现代编程特性,为开发者提供了一个更安全、…...

I.MX6ULL UART 串口通信实验
系列文章目录 I.MX6ULL UART 串口通信实验 I.MX6ULL UART 串口通信实验 系列文章目录一、前言二、I.MX6U 串口简介2.1 UART 简介2.2 I.MX6U UART 简介 三、硬件原理分析四、实验程序编写五、编译下载验证5.1编写 Makefile 和链接脚本5.2 编译下载 一、前言 不管是单片机开发还…...

systemctlm-cosim-demo项目分析
概述 systemctlm-cosim-demo项目是Xilinx的systemc库的demo工程。 环境安装 qemu安装 cd xilinx_proj/Downloads git clone https://github.com/Xilinx/qemu.git cd qemu git checkout 74d70f8008# Configure and build # zynq7000 # ./configure --target-list"arm-s…...
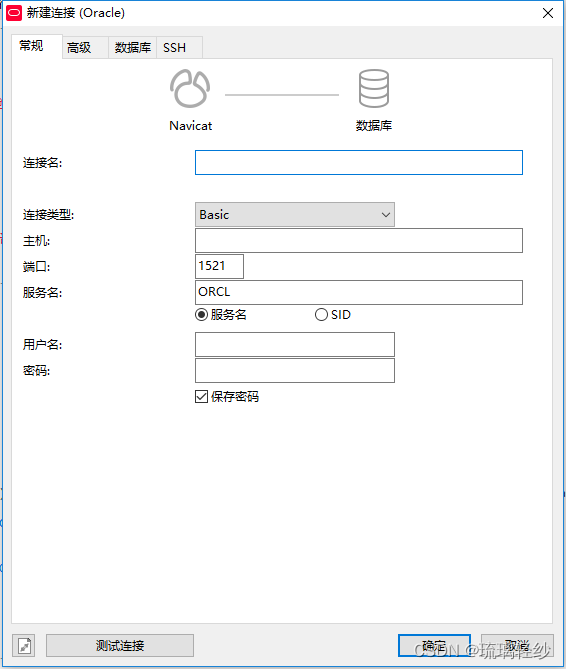
SQL学习小记(四)Navicat中连接Oracle数据库的详细步骤
五分钟解决Oracle连接问题:DPI-1047: Cannot locate a 64-bit Oracle Client library: “The specified module could not be SQL学习小记(四)Navicat中连接Oracle 1. 错误信息2. 解决过程2.1.版本查询2.2. 官网下载2.3. 设置Navicat的oci环…...

mysql聚簇索引
1.聚簇索引是物理索引,数据在表里是按顺序存储的,物理上是连续的,一般选主键id作为聚簇索引,且一张表里只能有一个聚簇索引。 2.只有InnoDB支持聚簇索引。 3.非聚簇索引是逻辑索引,将数据的某个字段抽取出来组成独立的…...

【云原生】Kubernetes----PersistentVolume(PV)与PersistentVolumeClaim(PVC)详解
目录 引言 一、存储卷 (一)存储卷定义 (二)存储卷的作用 1.数据持久化 2.数据共享 3.解耦 4.灵活性 (三)存储卷的分类 1.emptyDir存储卷 1.1 定义 1.2 特点 1.3 示例 2.hostPath存储卷 2.1 …...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
