二分搜索树深度优先遍历
二分搜索树深度优先遍历
二分搜索树(Binary Search Tree,简称BST)是一种特殊的二叉树,它具有以下特性:对于树中的任意节点,其左子树中的所有元素都小于该节点的值,其右子树中的所有元素都大于该节点的值。这种特性使得二分搜索树在查找、插入和删除操作中都能保持较高的效率。深度优先遍历(Depth-First Traversal)是二分搜索树的一种重要遍历方式,它包括前序遍历、中序遍历和后序遍历三种形式。
1. 前序遍历
前序遍历(Preorder Traversal)的顺序是:先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。这种遍历方式可以用来构建二分搜索树的先序序列。
算法步骤:
- 访问根节点。
- 前序遍历左子树。
- 前序遍历右子树。
示例代码(Python):
python def preorderTraversal(root): if root is None: return print(root.val, end=" ") preorderTraversal(root.left) preorderTraversal(root.right)
2. 中序遍历
中序遍历(Inorder Traversal)的顺序是:先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。中序遍历二分搜索树的结果是一个有序的数列。
算法步骤:
- 中序遍历左子树。
- 访问根节点。
- 中序遍历右子树。
示例代码(Python):
python def inorderTraversal(root): if root is None: return inorderTraversal(root.left) print(root.val, end=" ") inorderTraversal(root.right)
3. 后序遍历
后序遍历(Postorder Traversal)的顺序是:先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。后序遍历可以用来删除二分搜索树。
算法步骤:
- 后序遍历左子树。
- 后序遍历右子树。
- 访问根节点。
示例代码(Python):
python def postorderTraversal(root): if root is None: return postorderTraversal(root.left) postorderTraversal(root.right) print(root.val, end=" ")
总结
二分搜索树的深度优先遍历是树结构算法中的基础,理解和掌握这三种遍历方式对于后续学习树相关的算法和数据结构至关重要。在实际应用中,根据不同的需求选择合适的遍历方式,可以有效地提高算法的效率。
相关文章:

二分搜索树深度优先遍历
二分搜索树深度优先遍历 二分搜索树(Binary Search Tree,简称BST)是一种特殊的二叉树,它具有以下特性:对于树中的任意节点,其左子树中的所有元素都小于该节点的值,其右子树中的所有元素都大于该…...

ImportError: cannot import name ‘packaging‘ from ‘pkg_resources‘‘
参考自: [Bug]: ImportError: cannot import name packaging from pkg_resources (/usr/local/lib/python3.10/dist-packages/pkg_resources/__init__.py) Issue #15863 AUTOMATIC1111/stable-diffusion-webui GitHub ImportError: cannot import name packaging from pkg…...

灯塔歌曲音乐下载官网
灯塔歌曲音乐下载官网网址:www.dengtamp3.com 灯塔音乐下载上线以“用心服务,认真负责”为核心价值。 我们的团队是一个青春的团队,朝气蓬勃。我们采用最新的服务模式,以网为媒为广大客户提供服务,我们坚持以“用心&a…...

数据结构的归并排序(c语言版)
一.归并排序的基本概念 1.基本概念 归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下: 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。然后将这些子数组两两归并,得到有序的子数组。不断重复第二步,直到最终得到有序的整个数组。 2.核心…...

ubuntu使用Docker笔记
一、参考资料 1、B站视频 尚硅谷Docker实战教程 2、有心人整理的笔记 Docker笔记(周阳版) 3、菜鸟教程 Docker 教程 以下是本人的折腾实践。 二、Docker的安装 2.1、使用清华源安装docker,清华源官方教程。 本人是在ubuntu20.04下安装的…...

PHP编程入门:揭开Web开发的神秘面纱
PHP编程入门:揭开Web开发的神秘面纱 在数字化时代,PHP作为一种广泛使用的服务器端脚本语言,为Web开发领域注入了强大的活力。无论你是编程新手还是有一定经验的开发者,掌握PHP编程都将为你开启一扇通往Web开发新世界的大门。接下…...
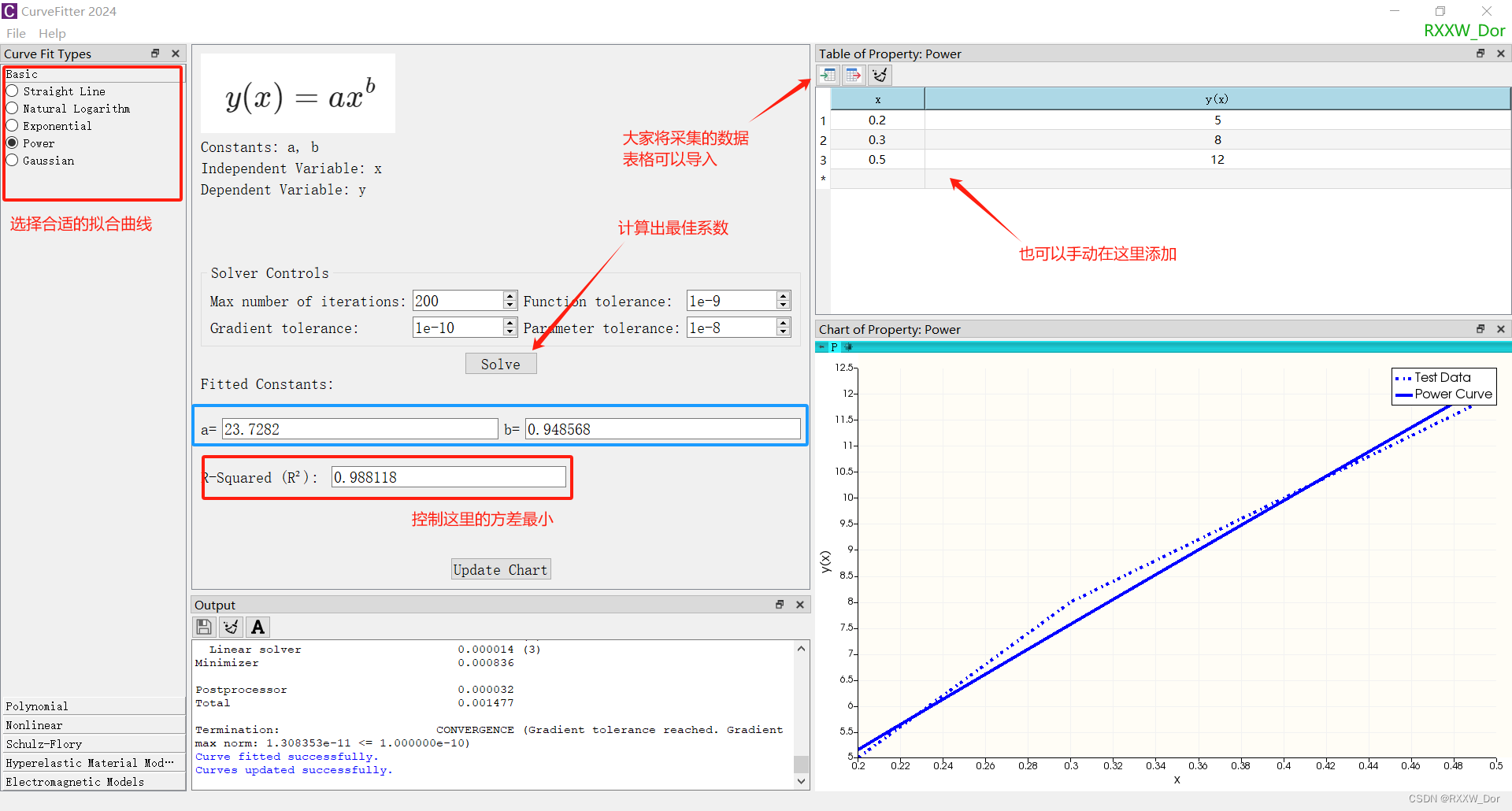
曲线拟合工具软件(免费)
曲线拟合是数据处理中经常用到的数值方法,本质是使用某一个模型(方程或者方程组)将一系列离散的数据拟合成平滑的曲线或者曲面,数值求解出对应的函数参数,大家可以利用MATLAB的曲线拟合工具箱也可以使用第三方的拟合软件,今天我们介绍Welsim免费的曲线拟合软件 1、MATLA…...
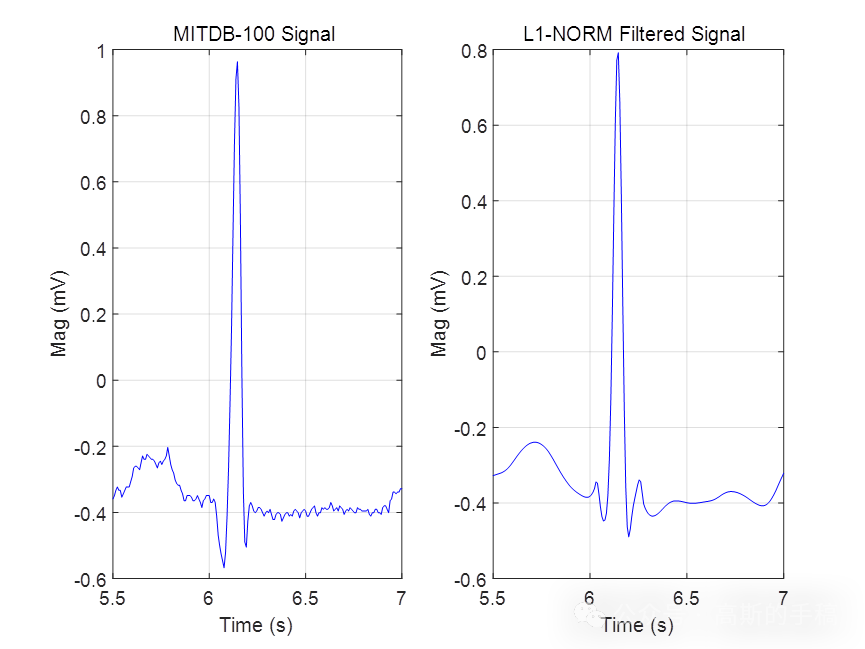
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一…...
)
Bitbucket的原理及应用详解(一)
本系列文章简介: 在数字化和全球化的今天,软件开发和项目管理已经成为企业成功的关键因素之一。随着团队规模的扩大和项目的复杂化,如何高效地协同开发、管理代码和确保代码质量成为了开发者和管理者面临的重要挑战。Bitbucket作为一款功能强…...

企业级win10电脑下同时存在Python3.11.7Python3.6.6,其中Python3.6.6是后装的【过程与踩坑复盘】
背景: 需要迁移原始服务器的上的Python3.6.6+Flask项目到一个新服务器上, 新服务器上本身存在一个Python3.11.7, 所以这涉及到了一个电脑需要装多个Python版本的问题 过程: 1-确定新电脑版本【比如是32还是64位】 前面开发人员存留了两个包,是python-3.6.6.exe和pytho…...

泛微开发修炼之旅--03常用数据表结构讲解
文章链接:泛微开发修炼之旅--03常用数据表结构讲解...

MySQL8找不到my.ini配置文件以及报sql_mode=only_full_group_by解决方案
一、找不到my.ini配置文件 MySQL 8 安装或启动过程中,如果系统找不到my.ini文件,通常意味着 MySQL服务器没有找到其配置文件。在Windows系统上,MySQL 8 预期使用my.ini作为配置文件,而不是在某些情况下用到的my.cnf文件。 通过 …...

Android 13 亮度调节代码分析
frameworks\base\packages\SystemUI\res\layout\quick_settings_brightness_dialog.xml 进度条控件 <com.android.systemui.settings.brightness.BrightnessSliderViewxmlns:android"http://schemas.android.com/apk/res/android"android:id"id/brightness…...
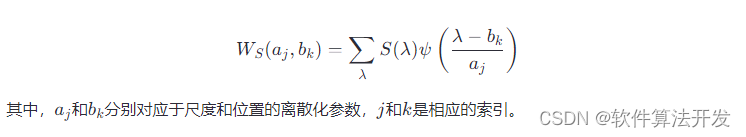
基于小波变换和峰值搜索的光谱检测matlab仿真,带GUI界面
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于小波变换和峰值搜索的光谱检测matlab仿真,带GUI界面.对光谱数据的成分进行提取,分析CO2,SO2,CO以及CH4四种成分比例。 2.…...

【初识Objective-C】
Objective-C学习 什么是OCOC的特性OC跑的第一个程序helloworld OC的一些基础知识标识符OC关键字数据类型字符型c字符串为什么NSString类型定义时前面要加和普通的c对象有什么区别 一些基础知识if语句switch语句三种循坏语句for循环:用于固定次数的循环while循环&…...
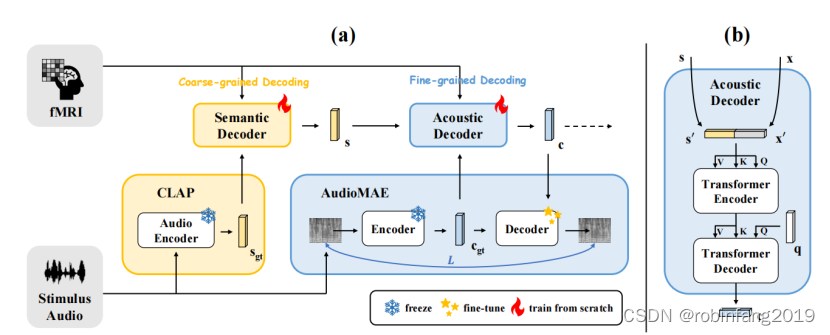
从功能性磁共振成像(fMRI)数据重建音频
听觉是人类最重要的感官之一,它负责接收外部的听觉刺激,并将这些信息传递给大脑进行处理和理解。研究人员正致力于从神经科学和计算机科学两个领域探索人脑的听觉感知机制。一个关键目标是从人脑中解码神经信息,并重建原始的刺激。常见的大脑…...

前端Vue小兔鲜儿电商项目实战Day04
一、二级分类 - 整体认识和路由配置 1. 配置二级路由 ①准备组件模板 - src/views/SubCategory/index.vue <script setup></script><template><div class"container"><!-- 面包屑 --><div class"bread-container">…...

TypeScript的简单总结
TypeScript 深度总结 引言 TypeScript,作为JavaScript的一个强类型超集,由Microsoft在2012年推出并维护至今,它不仅继承了JavaScript的所有特性,还引入了静态类型系统和其他现代编程特性,为开发者提供了一个更安全、…...

I.MX6ULL UART 串口通信实验
系列文章目录 I.MX6ULL UART 串口通信实验 I.MX6ULL UART 串口通信实验 系列文章目录一、前言二、I.MX6U 串口简介2.1 UART 简介2.2 I.MX6U UART 简介 三、硬件原理分析四、实验程序编写五、编译下载验证5.1编写 Makefile 和链接脚本5.2 编译下载 一、前言 不管是单片机开发还…...

systemctlm-cosim-demo项目分析
概述 systemctlm-cosim-demo项目是Xilinx的systemc库的demo工程。 环境安装 qemu安装 cd xilinx_proj/Downloads git clone https://github.com/Xilinx/qemu.git cd qemu git checkout 74d70f8008# Configure and build # zynq7000 # ./configure --target-list"arm-s…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
