Bowyer-Watson算法
数学原理及算法过程
Delaunay 三角剖分是一种特殊的三角剖分方法,它满足以下两个重要性质:
- 最大化最小角性质:Delaunay 三角剖分通过避免细长的三角形来最大化所有三角形的最小角。
- 空外接圆性质:在 Delaunay 三角剖分中,每个三角形的外接圆不包含任何其他点。这意味着,对于三角剖分中的任意三角形,其外接圆内没有其他输入点。
基于这些性质,Delaunay 三角剖分算法的一种实现方式是 Bowyer-Watson 算法,这是一种增量算法。以下是具体的算法步骤:
算法过程
- 初始化超级三角形:
- 创建一个足够大的超级三角形,包含所有输入点。这个三角形的三个顶点坐标远离实际输入点的范围,使其能够覆盖所有点。
- 逐点插入:
- 对于每个输入点,找到所有包含该点的外接圆的三角形。这些三角形被称为“坏三角形”。
- 构建多边形:
- 对于所有坏三角形,它们的每条边,如果只被一个坏三角形共享,则称其为边界边。这些边将形成一个多边形。
- 删除坏三角形:
- 将所有坏三角形从三角剖分中删除。
- 重新三角化多边形:
- 用新插入的点和多边形的边构成新的三角形,并将这些三角形加入三角剖分中。
- 移除超级三角形的影响:
- 在所有点都插入后,移除包含超级三角形顶点的所有三角形,得到最终的 Delaunay 三角剖分。
数学原理
-
外接圆计算:
- 对于每个三角形,计算其外接圆。外接圆的圆心(外心)和半径可以通过三角形顶点的坐标计算。
- 设三角形顶点为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1, y_1), (x_2, y_2), (x_3, y_3) (x1,y1),(x2,y2),(x3,y3)。外接圆的圆心 ( u , v ) (u, v) (u,v) 计算如下:
d = 2 ( x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) ) d = 2 \left( x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right) d=2(x1(y2−y3)+x2(y3−y1)+x3(y1−y2))
u = ( ( x 1 2 + y 1 2 ) ( y 2 − y 3 ) + ( x 2 2 + y 2 2 ) ( y 3 − y 1 ) + ( x 3 2 + y 3 2 ) ( y 1 − y 2 ) ) d u = \frac{((x_1^2 + y_1^2)(y_2 - y_3) + (x_2^2 + y_2^2)(y_3 - y_1) + (x_3^2 + y_3^2)(y_1 - y_2))}{d} u=d((x12+y12)(y2−y3)+(x22+y22)(y3−y1)+(x32+y32)(y1−y2))
v = ( ( x 1 2 + y 1 2 ) ( x 3 − x 2 ) + ( x 2 2 + y 2 2 ) ( x 1 − x 3 ) + ( x 3 2 + y 3 2 ) ( x 2 − x 1 ) ) d v = \frac{((x_1^2 + y_1^2)(x_3 - x_2) + (x_2^2 + y_2^2)(x_1 - x_3) + (x_3^2 + y_3^2)(x_2 - x_1))}{d} v=d((x12+y12)(x3−x2)+(x22+y22)(x1−x3)+(x32+y32)(x2−x1))
r = ( x 1 − u ) 2 + ( y 1 − v ) 2 r = \sqrt{(x_1 - u)^2 + (y_1 - v)^2} r=(x1−u)2+(y1−v)2
import matplotlib.pyplot as plt
import numpy as npclass Point:def __init__(self, x, y):self.x = xself.y = yclass Triangle:def __init__(self, p1, p2, p3):self.p1 = p1self.p2 = p2self.p3 = p3self.circumcenter, self.circumradius = self.circumcircle()def circumcircle(self):"""Calculate the circumcenter and circumradius of the triangle."""ax, ay = self.p1.x, self.p1.ybx, by = self.p2.x, self.p2.ycx, cy = self.p3.x, self.p3.yd = 2 * (ax * (by - cy) + bx * (cy - ay) + cx * (ay - by))ux = ((ax*ax + ay*ay) * (by - cy) + (bx*bx + by*by) * (cy - ay) + (cx*cx + cy*cy) * (ay - by)) / duy = ((ax*ax + ay*ay) * (cx - bx) + (bx*bx + by*by) * (ax - cx) + (cx*cx + cy*cy) * (bx - ax)) / dcircumcenter = Point(ux, uy)circumradius = np.sqrt((ax - ux)**2 + (ay - uy)**2)return circumcenter, circumradiusdef contains_point(self, p):"""Check if the point p is inside the circumcircle of the triangle."""return np.sqrt((p.x - self.circumcenter.x)**2 + (p.y - self.circumcenter.y)**2) < self.circumradiusdef delaunay_triangulation(points):"""Perform Delaunay triangulation on a set of points."""super_triangle = Triangle(Point(-1e5, -1e5), Point(1e5, -1e5), Point(0, 1e5))triangulation = [super_triangle]for p in points:bad_triangles = []for tri in triangulation:if tri.contains_point(p):bad_triangles.append(tri)polygon = []for tri in bad_triangles:for edge in [(tri.p1, tri.p2), (tri.p2, tri.p3), (tri.p3, tri.p1)]:is_shared = Falsefor other in bad_triangles:if other != tri and (edge in [(other.p1, other.p2), (other.p2, other.p3), (other.p3, other.p1)] or edge[::-1] in [(other.p1, other.p2), (other.p2, other.p3), (other.p3, other.p1)]):is_shared = Truebreakif not is_shared:polygon.append(edge)for tri in bad_triangles:triangulation.remove(tri)for edge in polygon:triangulation.append(Triangle(edge[0], edge[1], p))triangulation = [tri for tri in triangulation if not (super_triangle.p1 in [tri.p1, tri.p2, tri.p3] or super_triangle.p2 in [tri.p1, tri.p2, tri.p3] or super_triangle.p3 in [tri.p1, tri.p2, tri.p3])]return triangulationdef plot_triangulation(triangles, points):for tri in triangles:plt.plot([tri.p1.x, tri.p2.x], [tri.p1.y, tri.p2.y], 'b-')plt.plot([tri.p2.x, tri.p3.x], [tri.p2.y, tri.p3.y], 'b-')plt.plot([tri.p3.x, tri.p1.x], [tri.p3.y, tri.p1.y], 'b-')for p in points:plt.plot(p.x, p.y, 'ro')plt.show()
# Generate random points in the unit square
rectangle_corners = [Point(0, 0), Point(1, 0), Point(1, 1), Point(0, 1)]
random_points = [Point(np.random.rand(), np.random.rand()) for _ in range(20)]
points = rectangle_corners + random_pointstriangles = delaunay_triangulation(points)
plot_triangulation(triangles, points)

相关文章:

Bowyer-Watson算法
数学原理及算法过程 Delaunay 三角剖分是一种特殊的三角剖分方法,它满足以下两个重要性质: 最大化最小角性质:Delaunay 三角剖分通过避免细长的三角形来最大化所有三角形的最小角。空外接圆性质:在 Delaunay 三角剖分中…...

计算机基础之:fork进程与COW机制
在Unix-like操作系统中,fork()是一个系统调用,用于创建一个与调用进程(父进程)几乎完全相同的新进程(子进程),包括父进程的内存空间、环境变量、文件描述符等。这个过程是通过写时复制ÿ…...
47.各种类型的线程池
线程池继承体系 Executor(interface)->ExecutorService(interface)->ThreadPoolExecutor(class) Executors.newFixedThreadPool 核心线程数最大线程数(没有救急线程被创建),所以也无需超时时间阻塞队列LinkedBlockingQueue,可以放任意…...

多目标优化-NSGA-II
文章目录 一、前置知识NSGA-II帕累托前沿 二、算法流程1.NSGA2.NSGA-II 一、前置知识 1.NSGA(非支配排序遗传算法):旨在同时优化多个冲突的目标函数,寻找帕累托前沿上的解集。 什么是多个冲突的目标: 比如你看上了一辆车,你既想要它便宜,又…...

元宇宙数字藏品交易所,未来发展的大趋势
随着科技的飞速进步,元宇宙以其独特的魅力为数字世界绘制了一幅前所未有的宏伟蓝图。在这一宏大的背景下,数字藏品交易所作为连接虚拟与现实的桥梁,正以其卓越的优势,引领着数字藏品市场迈向新的高度。 首先,元宇宙为…...

通配符https数字证书260
随着越来越多的人开始使用互联网,互联网上的信息变得繁杂,用户很难识别网站信息的真实性,为了维护互联网的环境,开发者开始使用https证书对网站传输数据进行加密和身份认证,以此来保护用户的隐私以及标示网站的真实性。…...
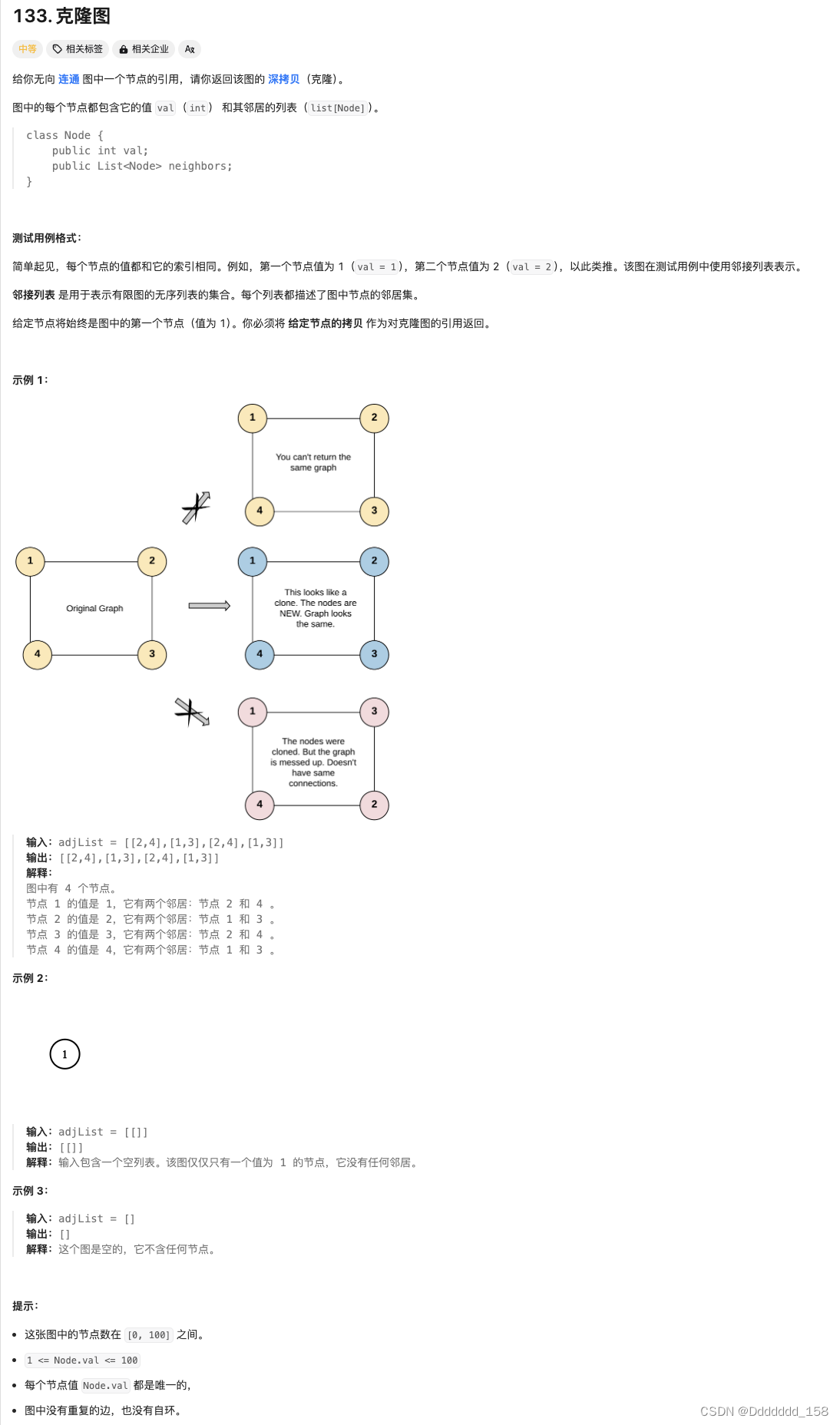
C++ | Leetcode C++题解之第133题克隆图
题目: 题解: class Solution { public:Node* cloneGraph(Node* node) {if (node nullptr) {return node;}unordered_map<Node*, Node*> visited;// 将题目给定的节点添加到队列queue<Node*> Q;Q.push(node);// 克隆第一个节点并存储到哈希…...

yangwebrtc x86_64环境搭建
版本:5.0.099 sudo apt-get install libxext-dev sudo apt-get install x11proto-xext-dev sudo apt-get install libxi-dev sudo apt install libasound2-dev sudo apt install libgl1-mesa-dev sudo apt-get install libxtst-dev 用qt打开以下两个项目的.pro met…...

前端面试题日常练-day53 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末 1. 在PHP中,以下哪个函数可以用于从一个数组的末尾删除一个元素并返回被删除的元素? a) array_pop() b) array_push() c) array_shift() d) array_unshift() 2. 在PHP中&…...
空间不够用了怎么办
空间告急啊哥们 整理一下清理空间有用的一些blog吧。 【linux】公共服务器如何清理过多的.cache缓存 linux根目录空间不足,追加空间到根目录下 【linux】linux磁盘空间 目录查看清理 和 文件查看清理...

pytorch数学操作
文章目录 1.torch.bitwise_not()2.torch.bitwise_and()3.torch.ceil()3.torch.clamp()4.torch.torch.floor() 1.torch.bitwise_not() 在 PyTorch 中,torch.bitwise_not() 是一个函数,用于执行逐元素的位非(bitwise NOT)操作。 t…...
如何做好电子内窥镜的网络安全管理?
电子内窥镜作为一种常用的医疗器械,其网络安全管理对于保护患者隐私和医疗数据的安全至关重要。以下是一些基本原则和步骤,用于确保电子内窥镜的网络安全: 1. 数据加密 为了防止数据泄露,电子内窥镜在传输患者图像数据时应采取有…...

Spring Boot项目中,如何在yml配置文件中读取maven pom.xml文件中的properties标签下的属性值
一、前言 在最近的项目开发过程中,有一个需求,需要在Spring Boot项目的yml配置文件中读取到mave的 pom.xml文件中的properties标签下的属性值,这个要怎么实现呢? 二、技术实践 pom.xml文件中增加测试属性 <properties><…...

C++:模板进阶
✨✨✨学习的道路很枯燥,希望我们能并肩走下来! 文章目录 文章目录 前言 一 非类型模板参数 二 模板的特化 2.1 概念 2.2 函数模板特化 函数模板的易错点 2.3 类模板特化 2.3.1 全特化 2.3.2 偏特化 部分特化 参数更进一步的限制 2.3.3 类模板特化应用示例…...

Linux 磁盘分区步骤
1.lsblk用于查看磁盘分区情况,lsblk -f用于查看uuid字符串以及挂载点。 以下是虚拟机部分添加磁盘的步骤。 其余没展示的都按照默认设置进入下一步即可。 2.添加完成后使用reboot重新进入后再使用lsblk就会发现磁盘sdb已经有了,但是没有分区。现在添加分…...
【TB作品】 51单片机8x8点阵显示滚动汉字仿真
功能 题目5基于51单片机LED8x8点阵显示 流水灯 直接滚动显示HELLO 直接滚动显示老师好 代码 void main( void ) {/** 移位后,右边的是第一个595,接收0X02,显示出0X02* 移位后,左边的是第2个595,接收0Xfe,…...
c++简略实现共享智能指针Shared_Ptr<T>
重点: 1.引用计数在堆上(原本应为原子变量) 2.引用计数增加减少需要加锁保证线程安全。 3.内部实现Release函数用于释放资源 4.未实现,增加自定义删除器可以将Release修改为模板函数,传入可调用参数。对于shared_p…...

2024会声会影全新旗舰版,下载体验!
在当今数字时代,视频内容已成为最受欢迎的媒介之一。无论是个人娱乐、教育还是商业推广,优秀的视频制作都是吸引观众的关键。为了满足广大用户对高质量视频制作软件的需求,我们隆重推出了会声会影2024最新旗舰版。这款软件不仅集成了最先进的…...

使用 Node.js 和 Azure Function App 自动更新 Elasticsearch 索引
作者:来自 Elastic Jessica Garson 维护最新数据至关重要,尤其是在处理频繁变化的动态数据集时。这篇博文将指导你使用 Node.js 加载数据,并通过定期更新确保数据保持最新。我们将利用 Azure Function Apps 的功能来自动执行这些更新…...
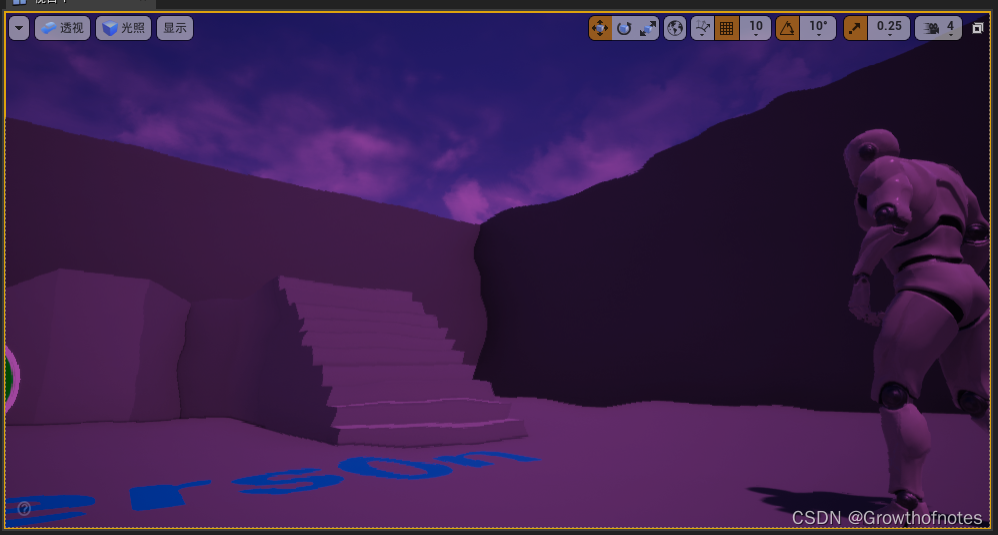
UE4_Ben_图形52_水下效果处理
学习笔记,不喜勿喷,欢迎指正,侵权立删!祝愿生活越来越好! 在这个后期处理的效果中,我们可以看到有很多不同的,这里有浓雾,波纹扭曲,镜头扭曲和边缘模糊,在第4…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
