PgMP考试结束后多久出成绩?附成绩查询方法
PgMP®考试结束后多久出成绩?这是许多参加PgMP®考试的考生都非常关心的问题。今天就给大家讲解一下PgMP®考试多久可以知道成绩?
一、PgMP®考试成绩查询时间
PgMP®考试一般在考试结束后的6-8周左右才会出成绩,届时PMI官方会通过电子邮件的形式提醒考生进行成绩查询。
二、PgMP®考试成绩查询方式
1、邮件查询
通常情况下,您会直接从“Project Management Institute (PMI)”收到一封成绩通知邮件。这封邮件的发件人明确标注为PMI,主题则为:“祝贺您获
得PgMP®认证”。邮件中,您会看到醒目的蓝色字体“成绩单”,只需轻轻点击,您将被直接导向PMI的官方网站,并展示您的成绩单。
2、PMI网站直接查询
若您希望通过PMI官网直接查询成绩,请按照以下步骤操作:
首先,打开PMI的官方网址:https://www.pmi.org。
在页面右上角,您会看到“Log in”字样,点击此处。
接下来,您需要输入自己的账号及密码进行登录。通常,您的账号就是您注册的邮箱地址。若您遗忘了密码,页面上也提供了“忘记密码”的选项,方便您找回密码。
登录成功后,再次点击右上角处的“My PMI”,随后选择“Dashboard”。在此页面,您便能清晰地看到自己的成绩页面。
进入成绩单后,若页面上方显示的是“PASS”,那么恭喜您,这表示您已通过考试,并获得了PgMP®认证;反之,若显示“FAIL”,则代表您此次考试未能通过。
三、PgMP®认证考试成绩合格标准
PgMP®考试不计算具体分数,考试结果分为“PASS”(通过)和“FAIL”(未通过)两种。考试成绩单上有各个领域考试结果饼状图,通过A、T、B、N四个等级来展示五大绩效领域的考试成绩,因此PgMP®考试最好成绩是5A。
PgMP®考试五大绩效领域分别为:
领域1:战略项目集管理
领域2:项目集生命周期
领域3:收益管理
领域4:干系人管理
领域5:治理
四、PgMP®考试未通过该怎么办?
PgMP®考试成绩没通过是可以申请重考的。报名重考仍需交报名费,不过比正式报名要便宜一些。
每位考生一年内最多能够申请两次重考,三次考试未通过的考生,间隔一年才能再次参加PgMP®考试。
PgMP®重考如何申请?
1、登录PMI网站考生个人账号,查看自己的英文报名是否过期;
2、确定自己英文报名资料还在一年有效期内后,提交重考申请表;
3、进去项目管理专业资格认证网站,登录考生个人账号,再次提交考试中文报名申请。
若在PgMP®认证考试资格一年有效期内可以不用提交英文申请材料,直接提交重考申请表,进行PgMP®重考中文报名就可以。若是超过一年有效期,则需要像初考一样,重新提交英文材料申请。有效期内申请重考费用:5600元/次,超出有效期申请重考7000元/次。
报名完成后,考生需登录“项目管理专业资格认证网站”上查看自己的考试状态,状态为已审核、已付费就是考试报名成功,若未通过审核则需要再次编辑报名资料提交申请,直到状态更改为已审核、已付费为止。
相关文章:

PgMP考试结束后多久出成绩?附成绩查询方法
PgMP考试结束后多久出成绩?这是许多参加PgMP考试的考生都非常关心的问题。今天就给大家讲解一下PgMP考试多久可以知道成绩? 一、PgMP考试成绩查询时间 PgMP考试一般在考试结束后的6-8周左右才会出成绩,届时PMI官方会通过电子邮件的形式提醒…...

springboot项目Redis统计在线用户
springboot项目Redis统计在线用户 我的项目有个显示用户的遗忘曲线,需要统计在线用户以计算他们的曲线 思考了两种方案,但都是用Redis的bitmap数据结构Bitmap是一种特殊类型的数组,其中每个元素只能存储0或1。在Redis中,Bitmap实际…...

GNeRF论文理解
文章目录 主要解决什么问题?结构设计以及为什么有效果?个人想法。 主要解决什么问题? 本文主要想要解决的问题是 如何使用uncalibrated的照片来进行Nerf重建。虽然说现在已经有了一些方式可以对相机位姿进行估计和优化,但是他们限…...
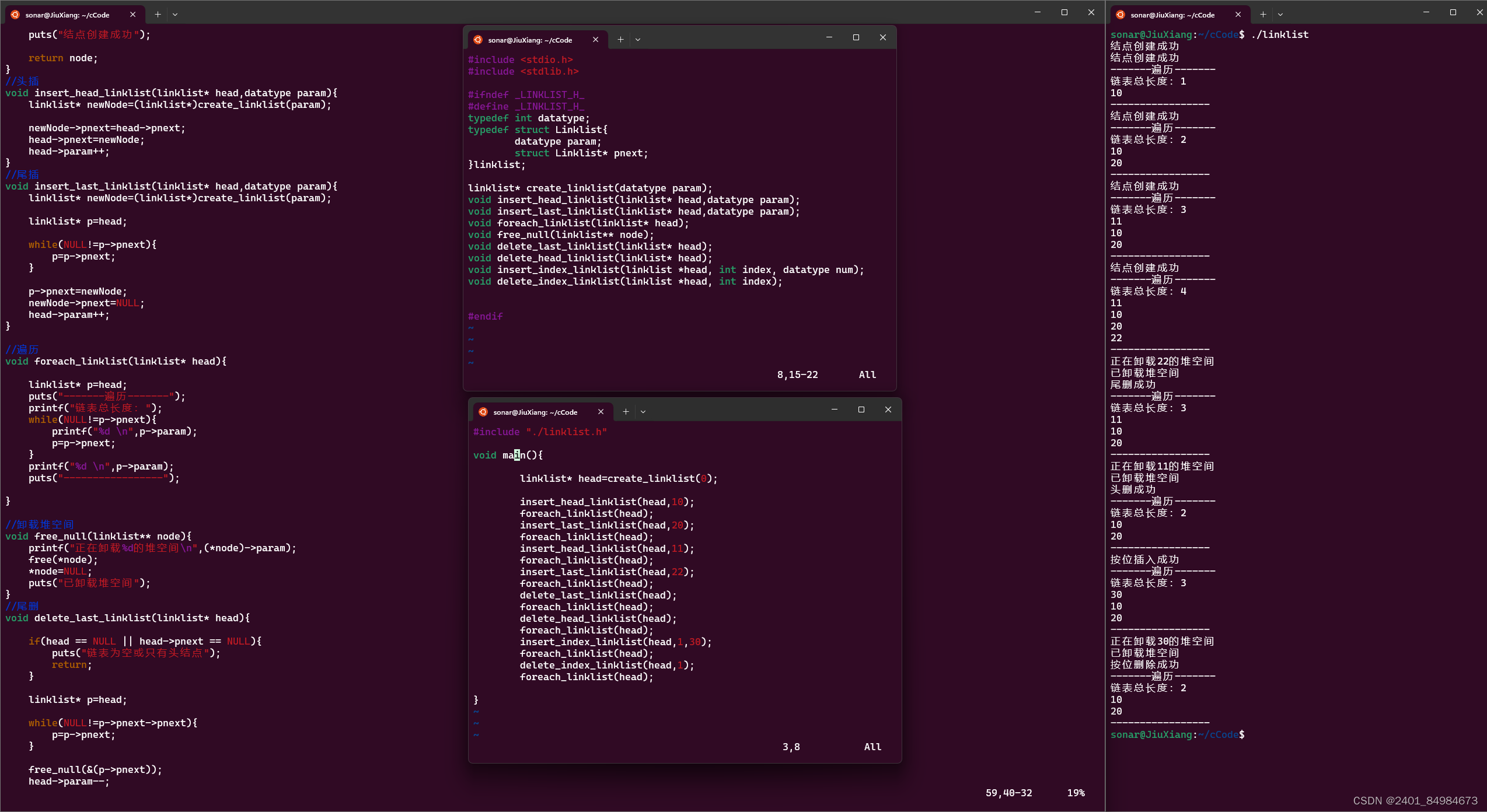
0531作业 链表
结果 整体代码 主要实现 /**实现* */ #include "./linklist.h"linklist* create_linklist(datatype param){linklist* node(linklist*)malloc(sizeof(linklist));if(NULLnode){puts("节点创建失败");}node->paramparam;node->pnextNULL;puts("…...
C++ STL - 容器
C STL(标准模板库)中的容器是一组通用的、可复用的数据结构,用于存储和管理不同类型的数据。 目录 零. 简介: 一 . vector(动态数组) 二. list(双向链表) 三. deque(…...
)
AI生成沉浸式3D世界(空间照片/视频)
面向Vision Pro等空间计算设备的产品指南 & 技术实现路径 一、通俗理解 ldi3格式概览:这是一种创新的3D内容格式,专为Vision Pro、Quest等VR头戴设备设计,让你能沉浸在一个几可乱真的三维世界,体验仿佛亲临其境的感受。 内容创作:利用开源工具,结合多角度摄像捕捉,…...

【Vue】异步更新 $nextTick
文章目录 一、引出问题二、解决方案三、代码实现 一、引出问题 需求 编辑标题, 编辑框自动聚焦 点击编辑,显示编辑框让编辑框,立刻获取焦点 即下图上面结构隐藏,下面结构显示,并且显示的时候让它自动聚焦。 代码如下 问题 “…...

【uCOS-III-编程指南】
uCOS-III-编程指南 ■ [野火]uCOS-III内核实现与应用开发实战指南■■■■ ■ [野火]uCOS-III内核实现与应用开发实战指南 添加链接描述 ■ ■ ■ ■...
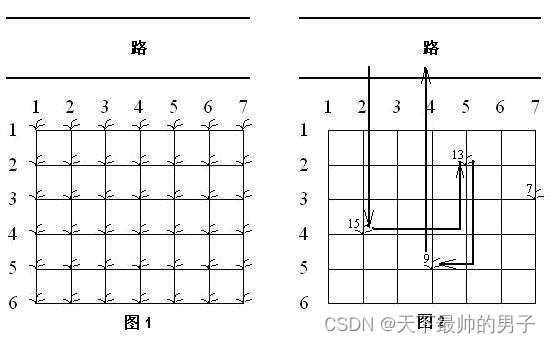
2004NOIP普及组真题 2. 花生采摘
线上OJ: 【04NOIP普及组】花生采摘 核心思想: 1、本题为贪心即可。 2、因为本题严格限制了顺序,所以先把每个节点的花生数量按降序排序。然后逐一判断下一个花生是否需要去采摘即可 3、每一次采摘完,记录耗时 t 以及采集的花…...
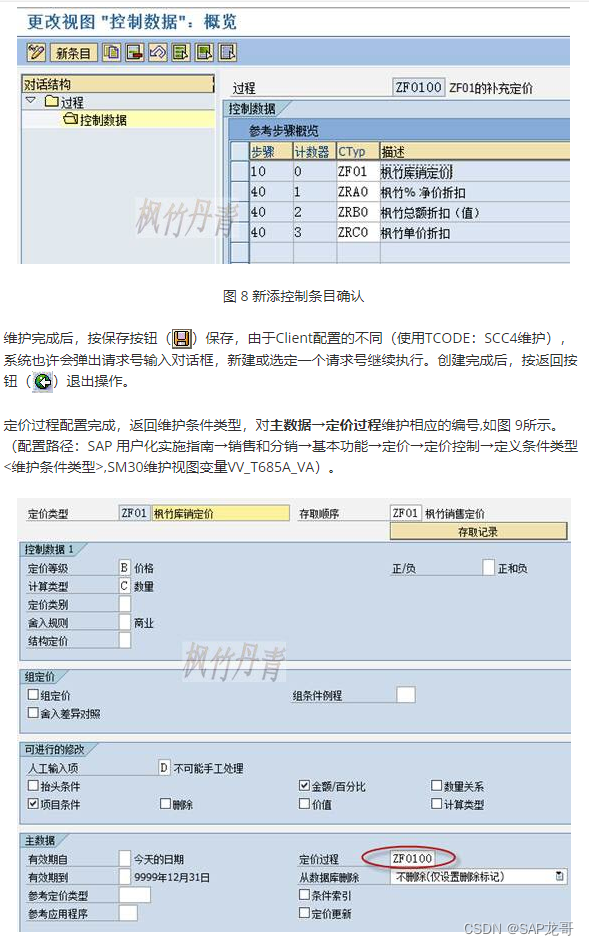
SAP-SD-21-定义用于定价补充的定价过程
图9 维护条件类型...
)
Android AAudio——C API创建AudioTrack(六)
虽然 AAudio 试图提供一种直接的硬件访问途径,但在某些场景下,如处理兼容性问题、使用系统服务(如 AudioFlinger)或者在某些设备上,使用 AudioTrack 可能是最有效或最合适的途径。这并不违背 AAudio 的初衷,因为它的目标是提供高性能的音频处理,而不是避免使用系统服务。…...

实验七、创建小型实验拓扑《计算机网络》
早检到底是谁发明出来的。 一、实验目的 完成本实验后,您将能够: • 设计逻辑网络。 • 配置物理实验拓扑。 • 配置 LAN 逻辑拓扑。 • 验证 LAN 连通性。 二、实验任务 在本实验中,将要求您连接网络设备并配置主机实现基本的网络…...

SqlServer2016企业版安装
前言 好久没有知识的累积,最近工作上遇到新的SqlServer2016安装,记录一下 参考文章 SQL Server 2016软件安装包和安装教程 - 哔哩哔哩 (bilibili.com) 安装包准备 需要提前准备软件安装包如下 cn_sql_server_2016_enterprise_x64_dvd_8699450&…...
)
HBase数据库面试知识点:第一部分 - 基础概念与特点(持续更新中)
目录 一、HBase基础概念 1. HBase定义 2. 核心组件 3. HBase的特点 二、HBase与传统RDBMS的区别 1. 数据类型 2. 数据操作 3. 存储方式 4. 伸缩性 5. 事务性 三、HBase数据模型 四、HBase的特点 五、HBase与Hadoop生态系统的关系 一、HBase基础概念 1. HBase定义 …...

一个高效的go语言字符串转驼峰命名算法实现函数
在go语言的开发中我们经常需要对各种命名进行规范, 今天给大家介绍的是一个高效的将字符串转 驼峰命名 (即 首字母大写的命名方式)的函数。 // 字符串转驼峰命名 // author tekintian <tekintiangmail.com> func CamelStr(str string) …...

Python中__init__方法的魔力:构建对象的基石
Python中__init__方法的魔力:构建对象的基石 在Python的世界中,__init__方法是一个特殊的存在。它不仅是类的构造函数,更是对象生命周期的起点。通过__init__方法,我们可以初始化对象的状态,设置属性,甚至…...
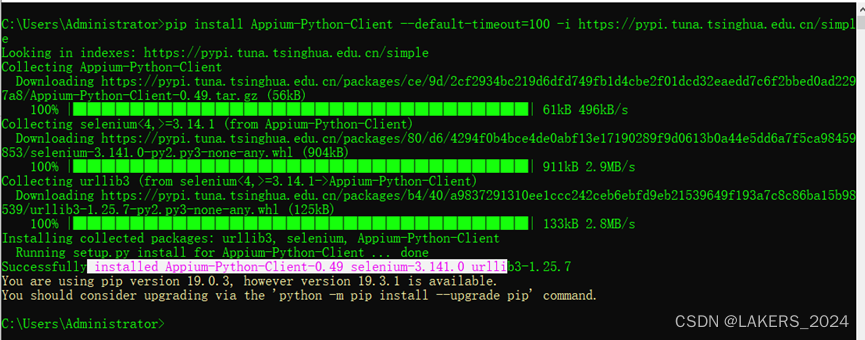
Appium安装及配置(Windows环境)
在做app相关自动化测试,需要使用appium来做中转操作,下面来介绍一下appium的环境安装配置 appium官方文档:欢迎 - Appium Documentation 一、下载appium 下载地址:https://github.com/appium/appium-desktop/releases?page3 通…...
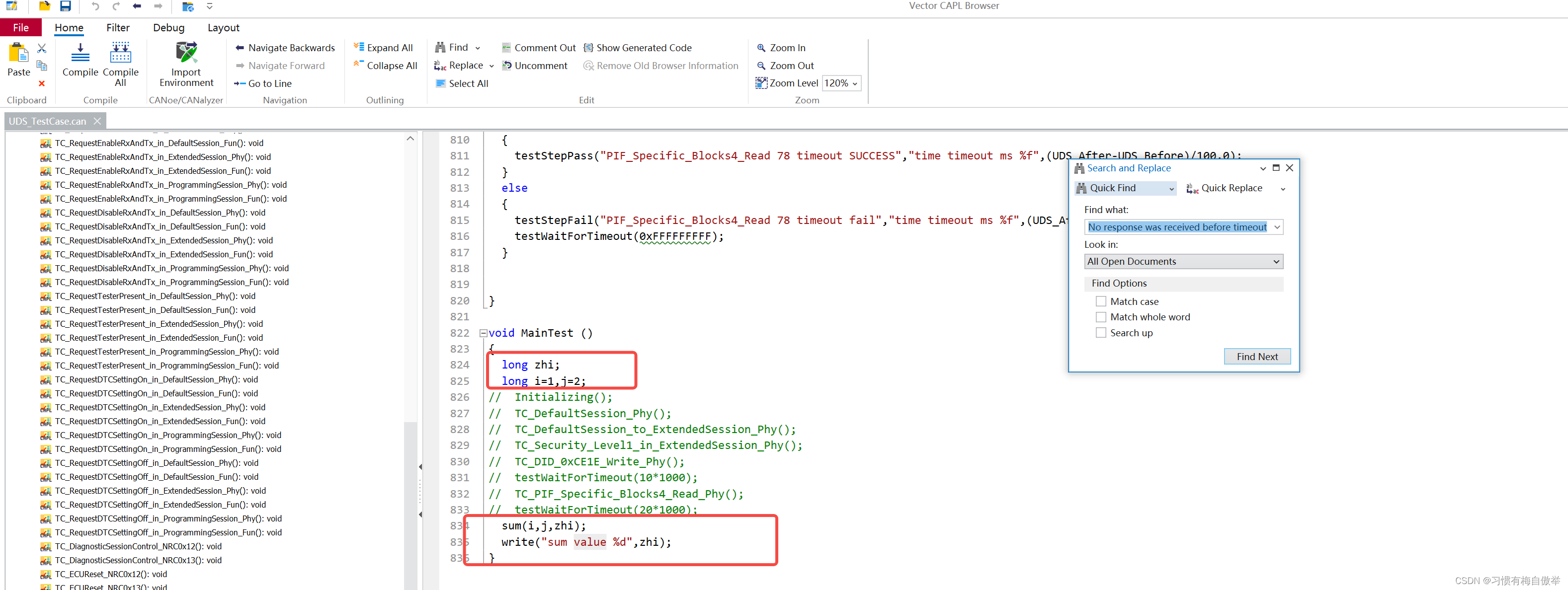
CANOE制造dll文件,以及应用dll文件
1、使用canoe自带的capl dll 2、然后使用Visual Studio 2022 打开项目 3、项目打开后修改下项目属性 4、修改capldll.cpp文件 4.1 添加的内容 void CAPLEXPORT far CAPLPASCAL appSum(long i, long j, long* s){*s i j;} {"sum", (CAPL_FARCALL)appSum, "…...

C++结合OpenCV进行图像处理与分类
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三…...

Master-Worker 架构的灰度发布难题
作者:石超 一、前言 Master-Worker 架构是成熟的分布式系统设计模式,具有集中控制、资源利用率高、容错简单等优点。我们数据中心内的几乎所有分布式系统都采用了这样的架构。  我们曾经发生过级联故障,造成了整个集群范围的服…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
