【数据结构】平衡二叉树(AVL树)
目录
前言
一、AVL树概念
二、AVL树节点定义
三、AVL树插入
1. 按照二叉搜索树的方式插入新节点
2. 维护节点的平衡因子与调整树的结构
a. 新节点插入较高左子树的左侧---左左:右单旋
b. 新节点插入较高右子树的右侧---右右:左单旋
c. 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
d. 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
四、AVL树删除
附录:AVL树实现参考代码
前言
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查 找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年发明了一种方法,用以解决上述问题。
一、AVL树概念
AVL 树是一种平衡二叉树,得名于其发明者的名字( Adelson-Velskii 以及 Landis)。(可见名字长的好处,命名都能多占一个字母出来)。平衡二叉树递归定义如下:
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
为了使AVL树保持平衡,在节点中增加了一个平衡因子作为节点属性。当树发生变化时,就通过维护平衡因子与改变树的结构来使树保持平衡。
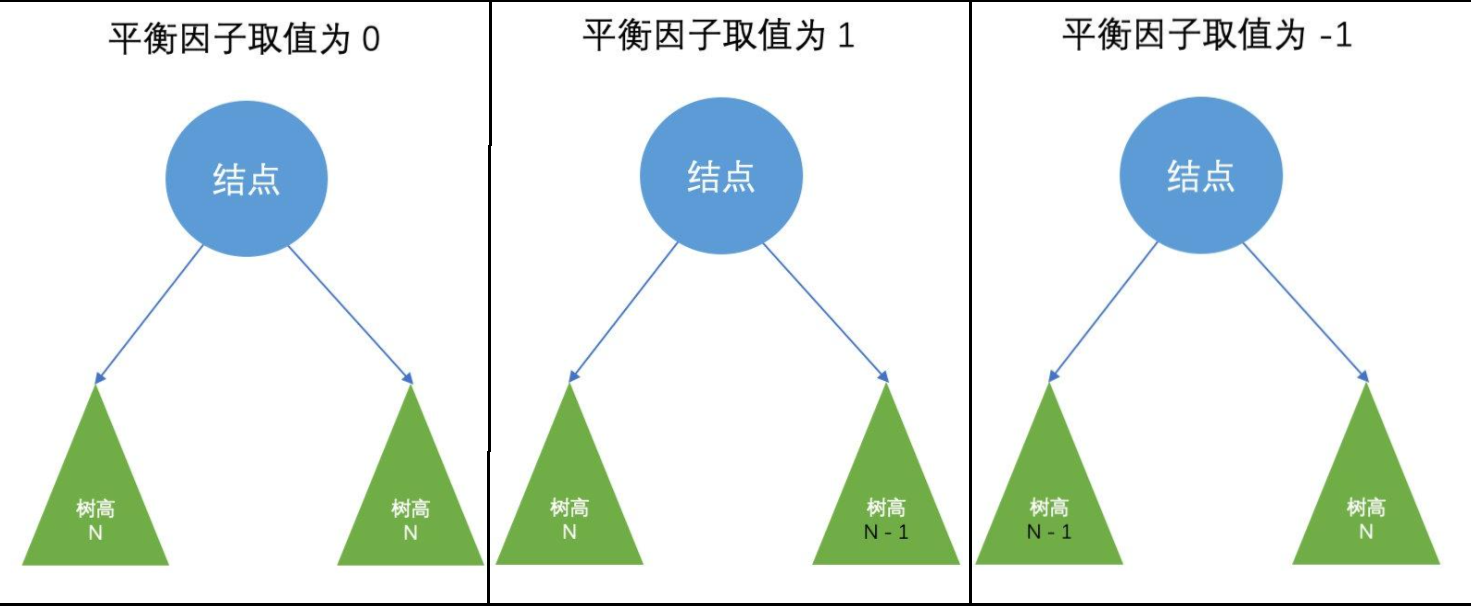
二、AVL树节点定义
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;std::pair<K, V> _kv;int _bf; //balance factorAVLTreeNode(const std::pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};三、AVL树插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么 AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
参考二叉搜索树。
【数据结构】二叉搜索树-CSDN博客![]() https://blog.csdn.net/lyhv_v/article/details/139243506
https://blog.csdn.net/lyhv_v/article/details/139243506
2. 维护节点的平衡因子与调整树的结构
cur插入后,pParent的平衡因子一定需要调整,在插入之前,pParent 的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:
- 如果pCur插入到pParent的左侧,只需给pParent的平衡因子-1即可
- 如果pCur插入到pParent的右侧,只需给pParent的平衡因子+1即可
此时:pParent的平衡因子可能有三种情况:0,正负1, 正负2
- 如果pParent的平衡因子为0,说明插入之前pParent的平衡因子为正负1,插入后被调整成0,此时满足 AVL树的性质,插入成功
- 如果pParent的平衡因子为正负1,说明插入前pParent的平衡因子一定为0,插入后被更新成正负1,此 时以pParent为根的树的高度增加,需要继续向上更新
- 如果pParent的平衡因子为正负2,则pParent的平衡因子违反平衡树的性质,需要对其进行旋转处理
a. 新节点插入较高左子树的左侧---左左:右单旋

Node* RotateR(Node* parent)
{Node* sub = parent->_left;Node* subR = sub->_right;if (parent == _root){_root = sub;sub->_parent = nullptr;}else{Node* up = parent->_parent;if (up->_kv.first > sub->_kv.first)up->_left = sub;elseup->_right = sub;sub->_parent = up;}parent->_left = subR;if (subR != nullptr)subR->_parent = parent;sub->_right = parent;parent->_parent = sub;parent->_bf = 0;sub->_bf = 0;return sub;
}b. 新节点插入较高右子树的右侧---右右:左单旋

Node* RotateL(Node* parent)
{Node* sub = parent->_right;Node* subL = sub->_left;if (parent == _root){_root = sub;sub->_parent = nullptr; }else{Node* up = parent->_parent;if (up->_kv.first > sub->_kv.first)up->_left = sub;elseup->_right = sub;sub->_parent = up;}parent->_right = subL;if (subL != nullptr)subL->_parent = parent;sub->_left = parent;parent->_parent = sub;parent->_bf = 0;sub->_bf = 0;return sub;
}c. 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
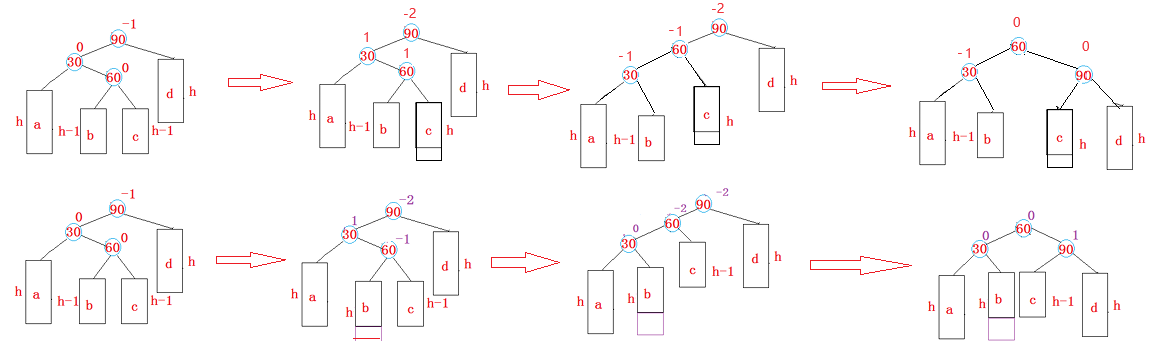
Node* RotateLR(Node* parent)
{Node* child = parent->_left;Node* sub = child->_right;Node* subL = sub->_left;Node* subR = sub->_right;if (parent == _root){_root = sub;sub->_parent = nullptr;}else{Node* up = parent->_parent;if (up->_kv.first > sub->_kv.first)up->_left = sub;elseup->_right = sub;sub->_parent = up;}sub->_right = parent;parent->_parent = sub;sub->_left = child;child->_parent = sub;parent->_left = subR;if (subR != nullptr)subR->_parent = parent;child->_right = subL;if (subL != nullptr)subL->_parent = child;if (sub->_bf == 1){parent->_bf = 0;child->_bf = -1;}else if (sub->_bf == -1){parent->_bf = 1;child->_bf = 0;}else{parent->_bf = 0;child->_bf = 0;}sub->_bf = 0;return sub;
}d. 新节点插入较高右子树的左侧---右左:先右单旋再左单旋

Node* RotateRL(Node* parent)
{Node* child = parent->_right;Node* sub = child->_left;Node* subL = sub->_left;Node* subR = sub->_right;if (parent == _root){_root = sub;sub->_parent = nullptr;}else{Node* up = parent->_parent;if (up->_kv.first > sub->_kv.first)up->_left = sub;elseup->_right = sub;sub->_parent = up;}sub->_left = parent;parent->_parent = sub;sub->_right = child;child->_parent = sub;parent->_right = subL;if (subL != nullptr)subL->_parent = parent;child->_left = subR;if (subR != nullptr)subR->_parent = child;if (sub->_bf == 1){parent->_bf = -1;child->_bf = 0;}else if (sub->_bf == -1){parent->_bf = 0;child->_bf = 1;}else{parent->_bf = 0;child->_bf = 0;}sub->_bf = 0;return sub;
}四、AVL树删除
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不 错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
具体实现可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
附录:AVL树实现参考代码
AVLTree · 梁羽赫/cpp_advanced - 码云 - 开源中国 (gitee.com)![]() https://gitee.com/yuhe-liang/cpp_advanced/tree/master/AVLTree
https://gitee.com/yuhe-liang/cpp_advanced/tree/master/AVLTree
相关文章:
【数据结构】平衡二叉树(AVL树)
目录 前言 一、AVL树概念 二、AVL树节点定义 三、AVL树插入 1. 按照二叉搜索树的方式插入新节点 2. 维护节点的平衡因子与调整树的结构 a. 新节点插入较高左子树的左侧---左左:右单旋 b. 新节点插入较高右子树的右侧---右右:左单旋 c. 新节点插入…...
python数据文件处理库-pandas
内容目录 一、pandas介绍二、数据加载和写出三、数据清洗四、数据转换五、数据查询和筛选六、数据统计七、数据可视化 pandas 是一个 Python提供的快速、灵活的数据结构处理包,让“关系型”或“标记型”数据的交互既简单又直观。 官网地址: https://pandas.pydata.o…...

stm32 h5 串口采用DMA循环BUFF接收数据
当使用STM32H5系列的MCU进行串口(USART)通信,并希望使用DMA(Direct Memory Access)进行循环缓冲区(Circular Buffer)接收数据时,你需要进行以下配置步骤: 初始化串口&…...

海外媒体通稿:9个极具创意的旅游业媒体推广案例分享-华媒舍
如今,旅游业正迅速发展,媒体推广成为吸引游客的关键。为了更好地展示旅游目的地,许多创意而富有创新的媒体推广策略应运而生。本文将介绍九个极富创意的旅游业媒体推广案例,为广大从业者带来灵感和借鉴。 1. 视频系列:…...

接口自动化框架封装思想建立(全)
httprunner框架(上) 一、什么是Httprunner? 1.httprunner是一个面向http协议的通用测试框架,以前比较流行的是2.X版本。 2.他的思想是只需要维护yaml/json文件就可以实现接口自动化测试,性能测试,线上监…...

char [] 赋新值
在C语言中,字符数组(char [])的值可以通过多种方式进行赋值。以下是一些常见的方法: 1、直接初始化: char str[50] "Hello, World!";2、使用strcpy()函数: char str[50]; strcpy(str, "…...

matlab计算图像信噪比SNR
直接上源码: close all clear all clc% 读取图像 I = imread(lena.bmp);I = rgb2gray(I); J =imnoise(I, salt & pepper, 0.001);...
DP读书:如何使用badge?(开源项目下的标咋用)
最近在冲论坛,很少更一些内容了。但遇到了一个真的有趣的: 开源项目下,蓝蓝绿绿的标是怎么用的呢? 这是我的主页Readme,在看一些NXP的主仓时,突然发现没有这个玩,就自己整了个 再比如我的CSDN专…...

使用JavaScript实现网页通知功能
如何使用js来实现网页通知功能。即使在用户浏览其他页面时,也能向他们推送通知信息。 废话不多说直接上代码 function showAutoNotification() {if ("Notification" in window) {Notification.requestPermission().then(function(permission) {if (permis…...

前端--导出
这边记录我们公司后端做的导出接口和前端是如何对接的 这边的技术栈是: 1: react 2: fetch 第一步:简单封装--导出界面 import { DrawerForm } from ant-design/pro-components; import { CloseOutlined } f…...

【数据库系统概论】触发器
【数据库系统概论】触发器 概述 在数据库系统中,触发器(Trigger)是一种特殊的存储过程,当特定事件在数据库表上发生时,会自动执行。触发器主要用于确保数据的完整性、一致性和实现复杂的业务规则。触发器是由用户定义…...
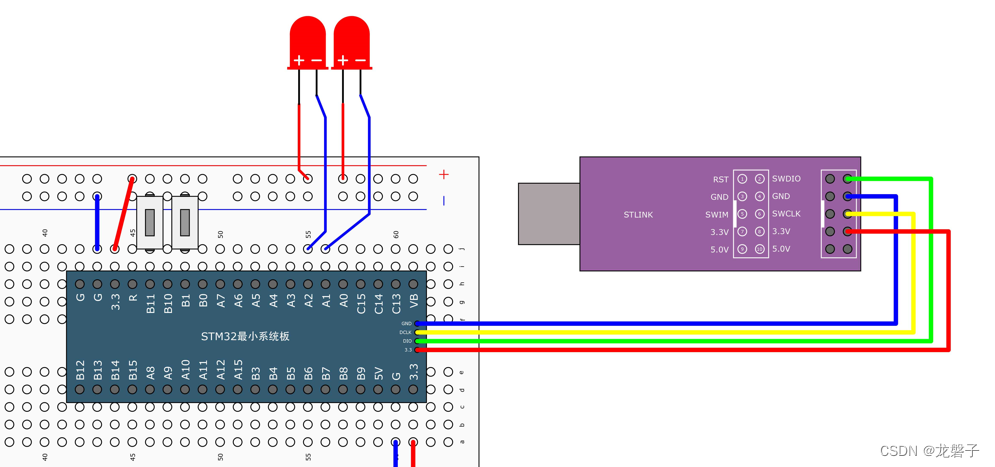
小白跟做江科大32单片机之按键控制LED
原理部分 1.LED部分使用的是这样的连接方式 2.传感器模块的电路图 滤波电容如果接地,一般用于滤波,在分析电路时就不用考虑。下面这个电路就是看A端和B端哪端的拉力大,就能把电压值对应到相应的电压值 比较器部分 如果A端电压>B端电压&am…...
-java文件输入输出流实验)
每天写java到期末考试(6.6)-java文件输入输出流实验
1、用字节流读写二进制文件 要求:用DataOutputStreamFileOutputStream类将1,2,…,100,这100个数字写入到文件 d:\out1.bin里,然后再用DatalnputStreamFilelnputStream类将d:\out1.bin的内读出来,并输出到屏幕上。 用DataOutputStreamFileOutputStream写入二进制数据时,直接调…...

Word2021中的The Mathtype DLL cannot be found问题解决(office 16+mathtype7+非初次安装)
问题描述,我的问题发生在word中无法使用自定义功能区中的mathtype 我的环境是:W11Word2021mathtype7 因为我是第二次安装mathtype7,所以我怀疑是因为没有卸载干净,于是我参考了下面这篇文章的做法 参考文章 1.首先重新卸载当前的…...

【Android面试八股文】在Java中传参数时是将值进行传递,还是传递引用?
在Java中传参数时是将值进行传递,还是传递引用? 这道题想考察什么? 是否了解什么是值传递和引用传递与真实场景使用,是否熟悉什么是值传递和引用传递在工作中的表现是什么? 考察的知识点 什么是值传递和引用传递的概念,两者对开发中编写的代码的影响 考生应该如何回…...
神经网络 torch.nn---Linear Layers(nn.Linear)
torch.nn - PyTorch中文文档 (pytorch-cn.readthedocs.io) torch.nn — PyTorch 2.3 documentation nn.Linear torch.nn.Linear(in_features, out_features, biasTrue, deviceNone, dtypeNone) 参数: in_features - 每个输入样本的大小out_features - 每个输出…...

PPT视频如何16倍速或者加速播放
有两种方式,一种是修改PPT本身,这种方式非常繁琐,不太推荐,还有一种就是修改视频本身,直接让视频是16倍速的视频即可。 如何让视频16倍速,我建议人生苦短,我用Python,几行代码&…...

【ai】DeepStream 简介
NVIDIA Metropolis 平台。 NVIDIA 大都会 利用视觉 AI 将来自数万亿物联网设备的数据转化为有价值的见解。 NVIDIA Metropolis 是一个应用程序框架、一套开发工具和合作伙伴生态系统,它将视觉数据和 AI 结合在一起,以提高各行各业的运营效率和安全性。它有助于理解数万亿个…...

如何学习使用淘宝API?淘宝API运营场景
学习使用淘宝API涉及对其功能、分类、调用方法及实际应用的综合理解。下面按部分详细解释如何系统地学习和掌握淘宝API的使用: 淘宝API接口入门 了解淘宝开放平台:淘宝开放平台为开发者提供了一个可以与淘宝数据进行交互的平台,涵盖了丰富的A…...

Java 面试题:Java 的动态代理是基于什么原理?
编程语言通常有各种不同的分类角度,动态类型和静态类型就是其中一种分类角度,简单区分就是语言类型信息是在运行时检查,还是编译期检查。 与其近似的还有一个对比,就是所谓强类型和弱类型,就是不同类型变量赋值时&…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
