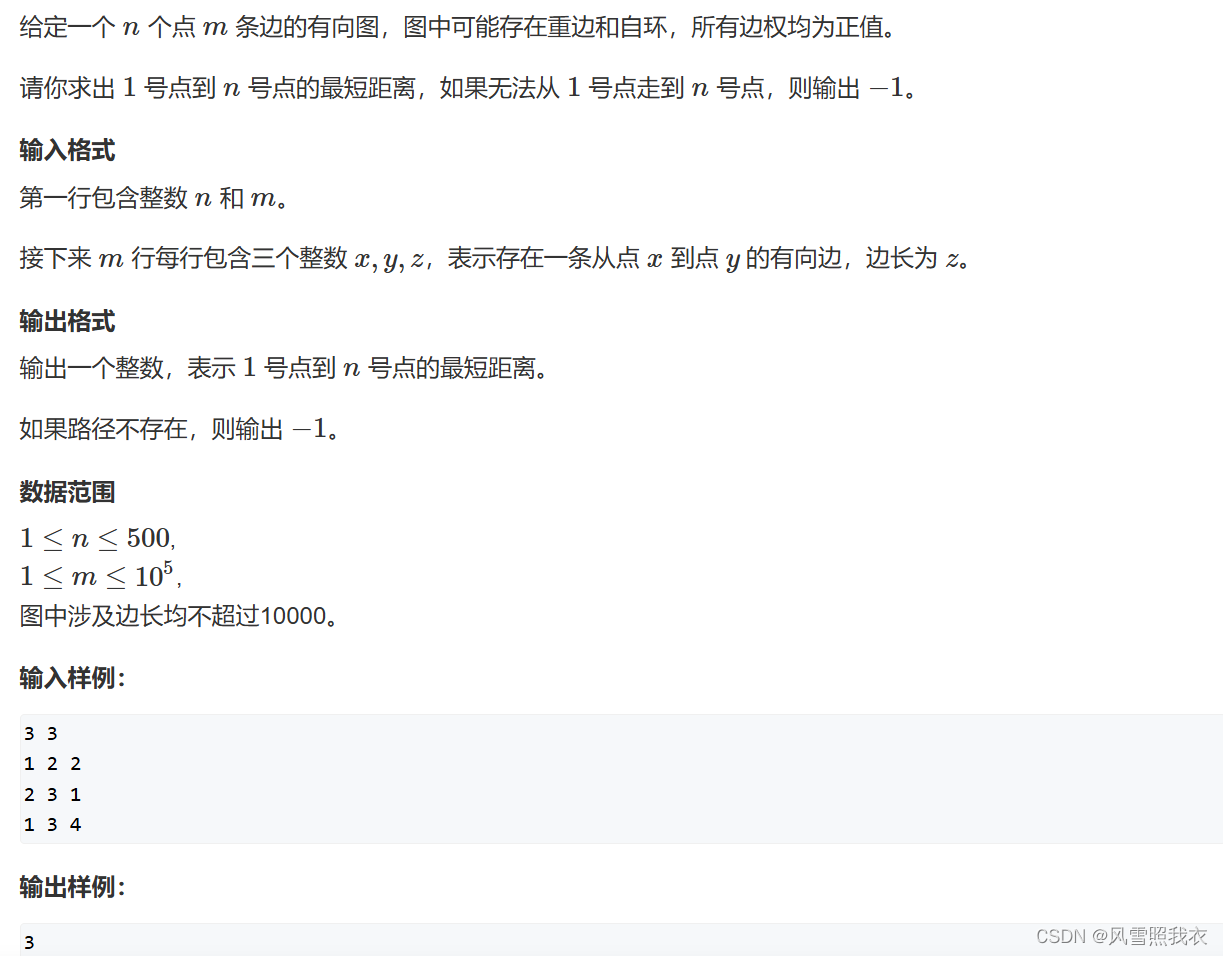
最短路问题
最短路问题是图论里非常经典的一个考点
接下来着重讲述五种求最短路的算法:朴素版dijkstra算法、堆优化版的dijkstra算法、bellman-ford算法、spfa算法、floyd算法
总体思维导图:
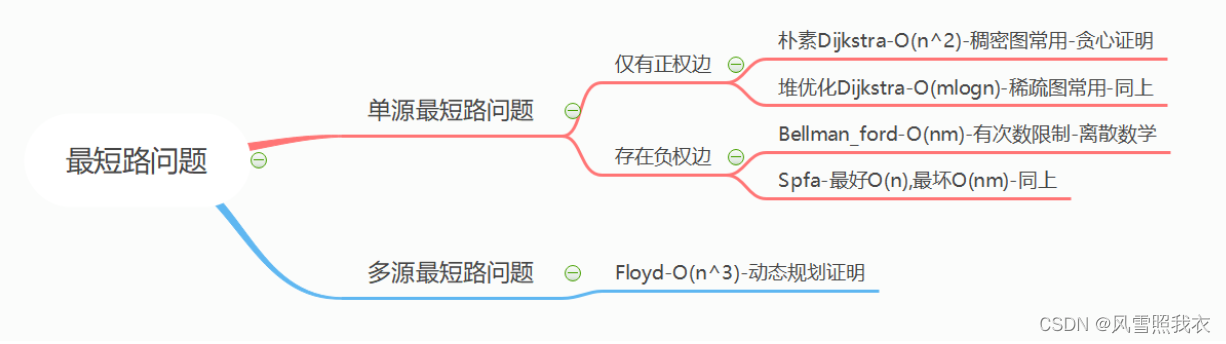
总体思路:
最短路分为两大类
{
在以下给出的时间复杂度中n表示图中的点数,m表示图中的边数
源点就是起点,汇点就是终点
①单源最短路{
求一个点到其它所有点的最短距离,(比如:从1号点到n的最短路问题)。
①{
1、所有边权都是正的
{
一、朴素的Dijkstra算法(O(n^2))
二、堆优化的Dijkstra算法(O(mlogn))
如果图上的边数越稠密(当m和n^2差不多的时候即为稠密图),那么堆优化版的要比朴素版的时间复杂度要高。反之如果边是稀疏的,那么尽量使用堆优化般的。
稠密图用邻接矩阵(矩阵),稀疏图用邻接表(链表)
朴素的Dijkstra板子:
void dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i ++ ){int t = -1; // 在还未确定最短路的点中,寻找距离最小的点for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;// 用t更新其他点的距离for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}}堆优化的Dijkstra板子:
int dijkstra()
{dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1}); // first存储距离,second存储节点编号while (heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;if (st[ver]) continue;st[ver] = true;for (int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}}
}
2、存在负权边
{
一、Bellman-Ford算法 O(nm)
二、SPFA 一般情况下O(m),最坏O(nm)。SPFA算法也就是对Bellman-Ford算法的优化,
若对边数进行了限制就不能使用SPFA算法,只能使用Bellman-ford算法。
一般情况下,题目中不会对边数进行限制,所以99%的情况SPFA算法要比Bellman-ford算法好用的多。
Bellman-Ford板子:备份
struct Edge
{//a,b,w从a走向b的边,权重是wint a,b,w;
}edges[M];int ballman_ford()
{memset(dist,0x3f,sizeof dist);dist[1]=0;//最多经历k次for(int i=0;i<k;i++){//先复制一层,防止串联memcpy(backup,dist,sizeof dist);for(int j=0;j<m;j++){//调用结构体auto e=edges[j];//等于上一个点+权重的值 与 当前这个点到原点的距离最小值dist[e.b]=min(backup[e.a]+e.w,dist[e.b]);}}SPFA板子:每个被更新的节点都用队列存储进来,注意使用st[ ]来优化,防止重复进入
void spfa()
{dist[1] = 0;queue<int> q;q.push(1);st[1] = true;while (q.size()){auto t = q.front();q.pop();st[t] = false;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入{q.push(j);st[j] = true;}}}}
}
}
}
}
②多源汇最短路{
不会像单源最短路那样只有一个起点。多源汇最短路可能有多个起点,对于多次询问,从其中一个点走到另外一个点的最短路问题,起点和终点都是不确定的
Floyd算法 O(N^3)
Floyd板子:三重循环
void floyd()
{for (int k = 1; k <= n; k ++ )for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
朴素版的dijkstra: O(MN)
题目:849. Dijkstra求最短路 I - AcWing题库
本题思路:
到起点的距离:dist[i]。已经确定了最短距离的点的集合:s[i]
第一步 先初始化距离:dist[1]=0,其余的dist[i]= +∞(比较大的数)
因为一开始只有起点的距离是被确定的了,其余的所有点都是不确定的
1号点到n号点最近的距离最近也就是n号点到1号点的距离最近,而由于这里1号点的到起点的距离已经确定所以一开始更新迭代就利用dist[1]已知的条件,来更新其他点到1号点的距离dist[x],然后再更新其他点到点x的距离即可。
这期间如果1号点到n号点的距离已经求出dist[n],且dist[x]<dist[n],那么dist[x]的距离就是确定了的(继续以这点迭代下去)。
如果不小于dist[n],那就没必要继续迭代下去,因为按照x的这条路径的长度会增加,那么就更一定不小于dist[n],所以更新到n号点时,那么n号点到1号点的距离也就最近了
第二步 是一个迭代循环的过程:
for(int i=0,i<n;i++)
{
t=不在s中的所有点中距离起点最近的点(距离最近的点)
s⬅t (如果有的话就把t加到s里面去)
更新dist[i](用t更新,即如果dist[i]>dist[t]+w(w是权重)就用t更新)
}
模拟:
在图论中寻找最短路的大体思维就是这样的,后面的算法也是如此,不在给出
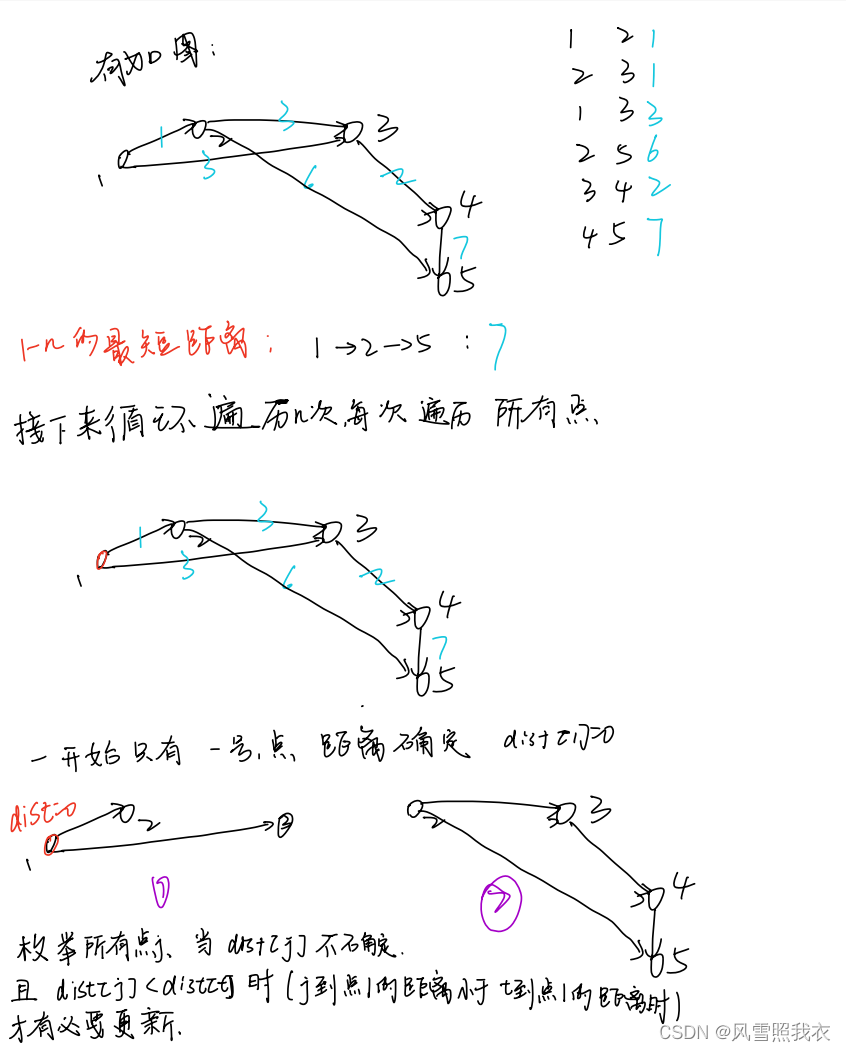

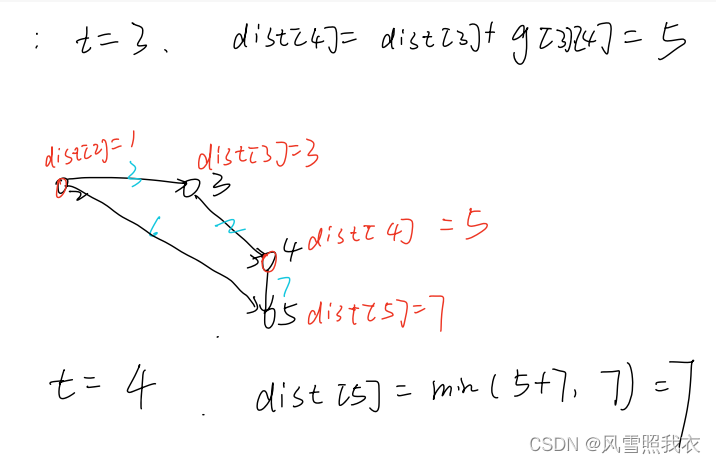
代码
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N=510;int n,m;
int g[N][N];
//到起点的距离
int dist[N];
bool st[N];int dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1]=0;//找到当前没有确定的点当中,距离起点最近的那个点(然后以这个点更新迭代之后的点)//如果已经确定了,那么就和dist[n]进行比较,来确定下一步是继续迭代还是结束这条路径for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j] && (t==-1 || dist[t] >dist[j]))//确定dist[j];t=j;}//已经确定了dist[t];st[t]=true;//更新每个点到1号点的距离for(int j=1;j<=n;j++){//使其等于(j号点到1号点的距离)与(t号点到1号点的距离+t号点到j号点距离的最小值)dist[j]=min(dist[j],dist[t]+g[t][j]);}}if(dist[n]==0x3f3f3f3f) return -1;else return dist[n];
}int main()
{cin >> n >> m;//初始化所有点之间的距离都为一个较大的数memset(g,0x3f,sizeof g);while(m--){int a,b,c;cin >> a >> b >> c;//防止重边g[a][b]=min(g[a][b],c);}cout << dijkstra();return 0;
}
堆优化版的dijkstra: O(mlogn)
题目:850. Dijkstra求最短路 II - AcWing题库

这里是稀疏图,使用邻接表来存
代码:
/*
n表示图中的点数,m表示图中的边数
一、朴素的Dijkstra算法(O(n^2))
二、堆优化的Dijkstra算法(O(mlogn))使用朴素版的dijkstra必定会爆掉,所以采用堆优化
由于点数和边数大致差不多,所以在这里是稀疏图→使用邻接表来存
这里采用优先队列。
*/#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>using namespace std;typedef pair<int,int> PII;
const int N=150010;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool st[N];void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}int dijkstra()
{dist[1]=0;//这里是小根堆,因为是从一号点开始priority_queue<PII,vector<PII>,greater<PII>> heap;
//这里先放距离,后放点的原因是pair<int,int>类的排序,是先比较的first,如果first相同才比较second//一号点,距离为0先放入队列中heap.push({0,1});while(heap.size()){auto t=heap.top();heap.pop();int ver=t.second,distance=t.first;//如果这个点已经使用过了的话,直接跳过if(st[ver]) continue;st[ver]=true;//使用这个点,以这个点为起点向下遍历//向下遍历,走到ver能走到的所有点for(int i=h[ver];i!=-1;i=ne[i]){//找出点坐标int tt=e[i];/*假设上一个点为x,下一个点为y。如果下一个点到原点的距离(dist[tt])大于(上一个点到原点的距离distance+x到y的距离(w[i]))时,才有更新的价值。*/if(dist[tt]>distance+w[i]){//符合,更新当前点到原点的距离dist[tt]=distance+w[i];//放入队列heap.push({dist[tt],tt});}}}if(dist[n]==0x3f3f3f3f) return -1;return dist[n];
}int main()
{scanf("%d%d",&n,&m);memset(dist,0x3f,sizeof dist);memset(h,-1,sizeof h);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);、//使用链表来存储add(a,b,c);}printf("%d\n",dijkstra());return 0;
}Bellman-ford算法
题目:853. 有边数限制的最短路 - AcWing题库
代码:
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;//点数,边数
const int N=510,M=10010;
int n,m,k;int dist[N],backup[N];struct Edge
{//a,b,w从a走向b的边,权重是wint a,b,w;
}edges[M];int ballman_ford()
{memset(dist,0x3f,sizeof dist);dist[1]=0;//最多经历k次for(int i=0;i<k;i++){
//复制一份,防止串联memcpy(backup,dist,sizeof dist);for(int j=0;j<m;j++){auto e=edges[j];dist[e.b]=min(backup[e.a]+e.w,dist[e.b]);}}if(dist[n] > 0x3f3f3f3f /2) cout << "impossible" << endl;else cout << dist[n];
}int main()
{cin >> n >> m >> k;for(int i=0;i<m;i++){int a,b,c;cin >> a >> b >> c;edges[i]={a,b,c};}ballman_ford();return 0;
}
SPFA算法:
题目:851. spfa求最短路 - AcWing题库
模拟:
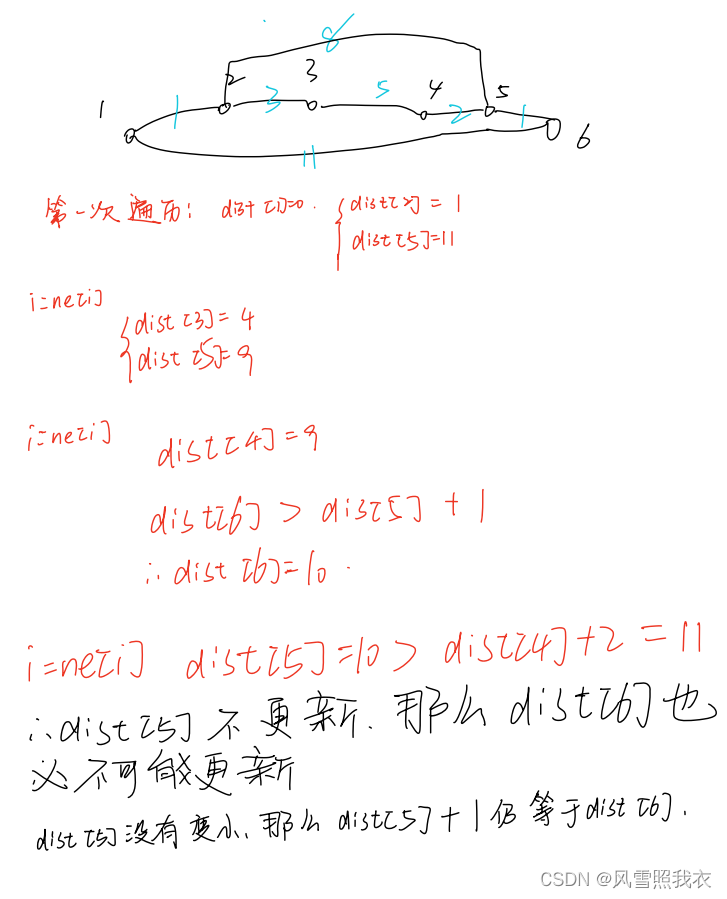
代码:
/*
每次将变小了的节点入队,那么用此节点更新后面的节点时才有可能将后面的数值变小
否则,若此节点都没变小,那么后面的节点不一定会因为被此节点更新而变小
即优化的是Bellman-ford算法里的这一步:for (int i = 0; i < n; i ++ )for (int j = 0; j < m; j ++ )
这里并不能保证每一次的j循环都有节点被更新,从而增加时间复杂度(公司的总效益涨了,员工的工资才有可能会涨,即前面的点的dist数值减小了,后面的数值才可能会减小)
省去了因为没有被更新而重复的操作
但是如果出题人卡你,时间复杂度和bellman-ford算法一致O(nm),最好的情况为O(m);
*/#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>using namespace std;int n,m;
const int N=1e5+10;
int e[N],ne[N],h[N],idx,w[N];
queue<int> q;
bool st[N];
int dist[N];
//使用链表进行储存
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}void spfa()
{memset(dist,0x3f,sizeof dist);dist[1]=0;q.push(1);//使用过1号节点,则为truest[1]=true;while(q.size()){int t=q.front();q.pop();/*取出来头节点之后,那么在队列中的头节点会被删除,也就需要清空其使用情况以方便下次的入队(只要这个节点变小了,那么就可以用它来再次更新后面的节点)也就是再次入队*/st[t]=false;//从头结点开始遍历,使用队列中的节点依次更新后面的值的大小for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];if(!st[j]){q.push(j);st[j]=true;}}}}//由于每次更新都是由队列里的数来更新,所以如果抵达不到n的话,那么n号点一定没有被更新if(dist[n]==0x3f3f3f3f) cout << "impossible" << endl;else cout << dist[n];
}int main()
{memset(h,-1,sizeof h);cin >> n >>m;while(m--){int a,b,c;cin >> a >> b >> c;add(a,b,c);}spfa();return 0;
}题目:852. spfa判断负环 - AcWing题库

这里再寻找最短路时,如若存在负环,那么会一直绕着这个负环来循环(因为这样可以使距离无限变小)
代码:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>using namespace std;const int N=10010;
int n,m;
int e[N],ne[N],h[N],w[N],idx;
//cnt[]表示当前最短路的边数
int dist[N],cnt[N];
bool st[N];
queue<int> q;void add(int a,int b,int c)
{e[idx]=b,ne[idx]=h[a],w[idx]=c,h[a]=idx++;
}bool spfa()
{//负环所在的位置可能是头节点抵达不到的,所以一开始将所有点全部放进队列中for(int i=1;i<=n;i++){//标记为true,表示该节点已经被放进了队列里st[i]=true;q.push(i);}while(q.size()){int t=q.front();q.pop();st[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];cnt[j]=cnt[t]+1;//如果不存在负环的话,那么从一个节点出发后所遍历的边数一定小于n//否则的话就一定存在负环if(cnt[j]>=n) return true;if(!st[i]){q.push(j);st[j]=true;}}}}return false;
}int main()
{memset(h,-1,sizeof h);cin >> n >> m;while(m--){int a,b,c;cin >> a >> b >> c;add(a,b,c);}if(spfa()) puts("Yes");else puts("No");return 0;
}Floyed算法:
这里的证明使用dp来论证的,建议直接背板子
题目:854. Floyd求最短路 - AcWing题库

代码:
/*
②多源汇最短路{不会像单源最短路那样只有一个起点。多源汇最短路可能有多个起点,对于多次询问,从其中一个点走到另外一个点的最短路问题,起点和终点都是不确定的Floyd算法 O(N^3)}用邻接矩阵存储所有的边d[][]for(k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j])}}}循环完之后d[i][j]就是从i到j的最短路径
*/#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;const int N=210,INF=1e9;
int d[N][N];
int n,m,Q;void floyd()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}
}int main()
{cin >> n >> m >> Q;//初始化for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){//自环的距离初始化为0if(i==j) d[i][j]=0;//其余的初始化为正无穷else d[i][j]=INF;}}while(m--){int a,b,c;cin >> a >> b >> c;//对于重边来说取一个最小值即可d[a][b]=min(d[a][b],c);}floyd();while(Q--){int a,b;cin >> a >> b;//存在负权边时距离的大小不等于INFif(d[a][b]>INF/2) cout << "impossible" << endl;else cout << d[a][b] << endl;}return 0;
}tips:
图论这一节重在代码实现,很多板子都是互相重复的。
至于该思路如何实现的,可以课下钻研
相关文章:

最短路问题
最短路问题是图论里非常经典的一个考点 接下来着重讲述五种求最短路的算法:朴素版dijkstra算法、堆优化版的dijkstra算法、bellman-ford算法、spfa算法、floyd算法 总体思维导图: 总体思路: 最短路分为两大类 { 在以下给出的时间复杂度中n…...

spark MLlib 中的分类模型
理解这些机器学习模型的数学原理需要一定的数学基础,下面我将简要介绍每个模型的数学原理,并附上相关的数学公式。 1. LinearSVC(线性支持向量机) 数学原理: 线性支持向量机的目标是找到一个超平面,最大化…...

24上半年报考人数“不增反降”?备考下半年软考的难了......
近日,工信教考发布了一篇《2024年上半年计算机软件资格考试顺利举行》的文章,公布了2024年上半年软考报考人数共计52.77万人,其中,初级资格5.12万人、中级资格24.37万人、高级资格23.28万人。 软考高级占总报名人数的44%…...
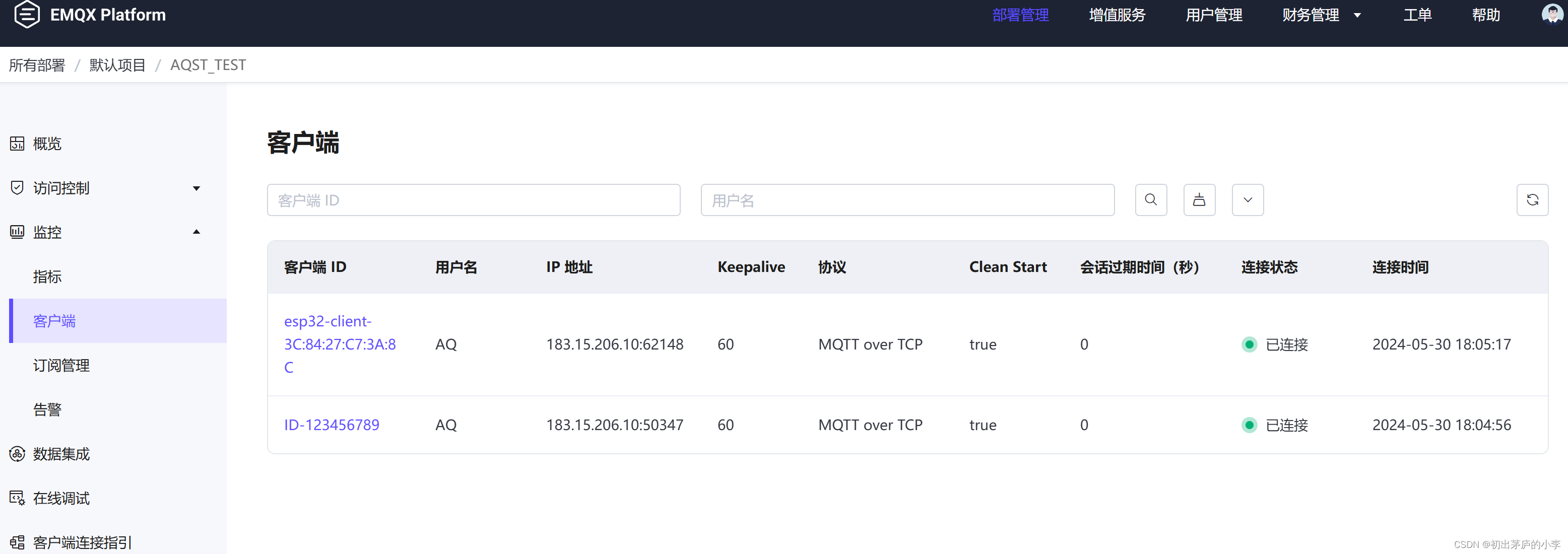
初出茅庐的小李博客之使用立创开发板(ESP32)连接到EMQX Platform【MQTT TLS/SSL 端口连接】
介绍 手上有一块立创开发板,本着不吃灰的原则把它用起来,今天就来用它来连接上自己部署的MQTT服务器进行数据通信。 硬件:立创开发板 开发环境:Arduino IDE Win11 MQTT 平台:EMQX Platform 立创开发板介绍࿱…...

js平滑滚动元素使其可见
直接上重点: let xpath "//*/div[idxxx]"; document.evaluate(xpath, document, null, XPathResult.FIRST_ORDERED_NODE_TYPE, null).singleNodeValue.scrollIntoView({ behavior: "smooth"})这段代码是JavaScript中使用XPath查询文档并执行平…...

TP6 事件绑定、监听、订阅
事件绑定与监听 命令行生成事件类 php think make:event EventDemo 命令行生成事件监听类php think make:listener ListenerDemo 事件类可作为保存与事件相关信息的容器,如没有额外需求可以不需要定义 事件系统的所有操作都通过think\facade\Event类进行静态调用 当定义…...

SpringCloud Gateway中Filters详细说明
前面 https://blog.csdn.net/J080624/article/details/139494909 我们研究了GateWay中各种路由断言的使用。SpringCloud GateWay 还提供了各种过滤器用来对请求和响应进行处理。 官网地址:SpringCloud Gateway Filter 【1】GatewayFilter Factories 路由过滤器允…...

力扣2156.查找给定哈希值的子串
力扣2156.查找给定哈希值的子串 rolling hash:求带权的值 左边是高位 右边是低位 本题要求左边低位 只要反向求即可 class Solution {public:string subStrHash(string s, int power, int modulo, int k, int hashValue) {int n s.size();long long M modulo,p…...
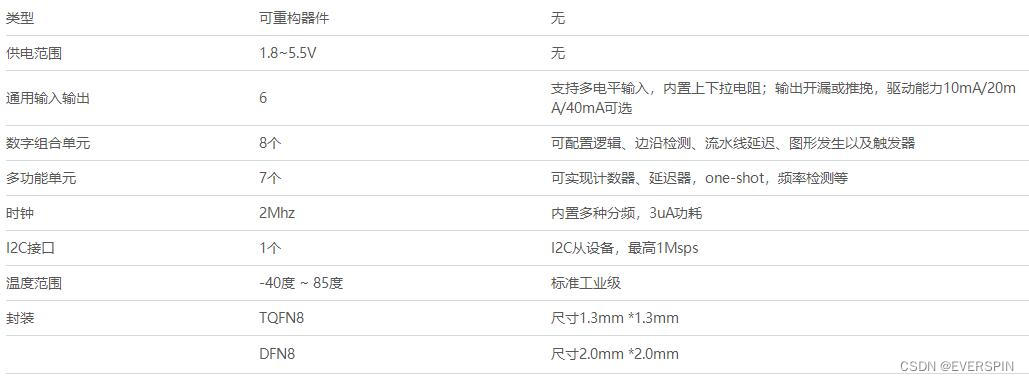
推荐低成本低功耗的纯数字现场可重构IC
CPLD采用CMOS EPROM、EEPROM、快闪存储器和SRAM等编程技术,从而构成了高密度、高速度和低功耗的可编程逻辑器件。 RAMSUN提供的型号LS98003是通用可配置的数字逻辑芯片,有体积小、超低功耗和高可靠性等特点。客户可以根据自己的功能需求设计芯片&#x…...

解决change事件与blur事件互不影响
<template><div style"margin-top: 40px"><el-selectv-model"form.name"placeholder"请选择名称"clearablefilterableref"selectName"allow-createblur"nameBlur($event)"visible-change"visibleNameCh…...

后端开发面经系列 -- 同程旅行C++一面
同程旅行C一面 公众号:阿Q技术站 文章目录 同程旅行C一面1、sizeof与strlen的区别?2、运算符和函数有什么区别?3、new和malloc?4、内存泄漏与规避方法?5、悬空指针与野指针?6、手撕冒泡排序?7、…...

推荐几个开源的c#的工作流引擎组件
以下是一个.NET Core领域可以推荐使用的流程引擎的表格: 名称 生产厂家 下载地址 支持二开 独立部署 ccflow 济南驰骋信息技术有限公司 https://gitee.com/opencc 是 是 Elsa Elsa Workflows GitHub - elsa-workflows/elsa-core: A .NET workflows li…...
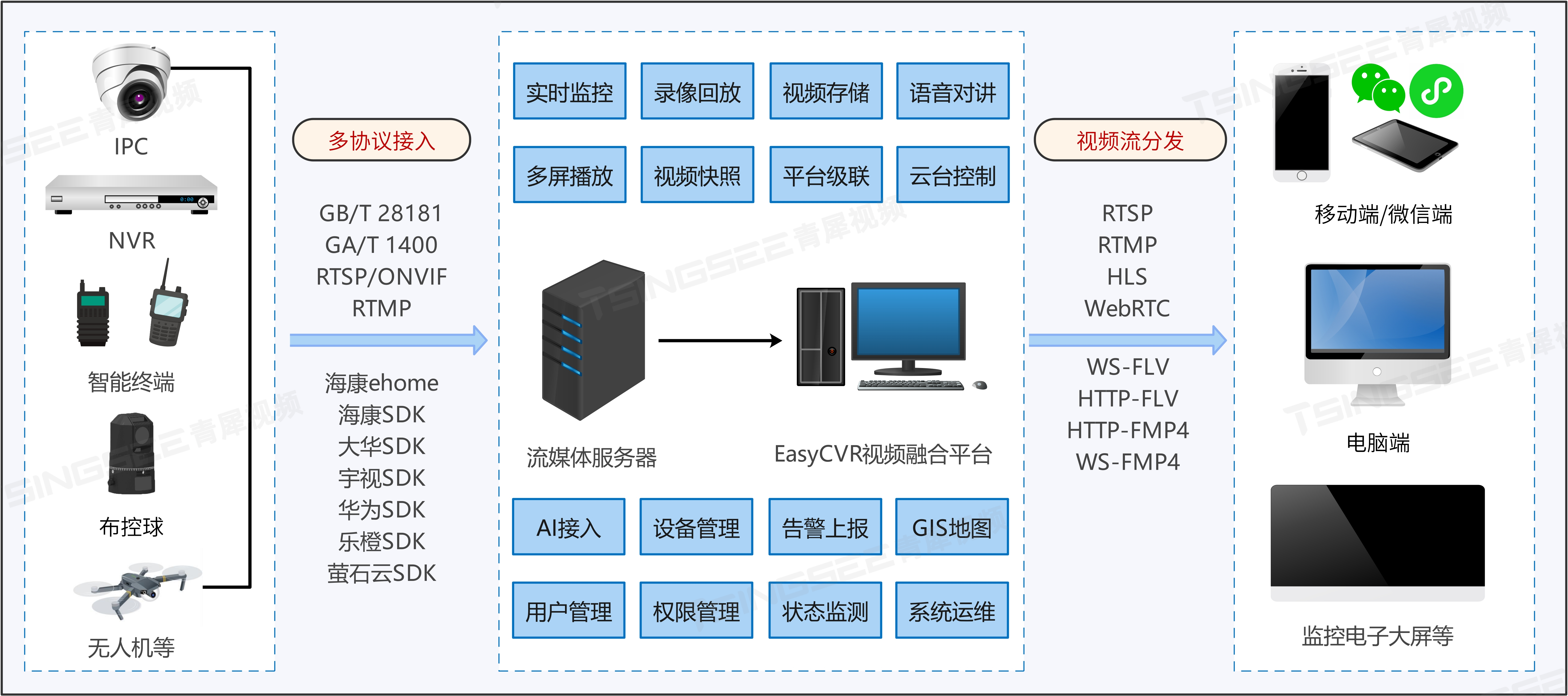
视频汇聚EasyCVR视频监控云平台对接GA/T 1400视图库对象和对象集合XMLSchema描述
GA/T 1400协议主要应用于公安系统的视频图像信息应用系统,如警务综合平台、治安防控系统、交通管理系统等。在城市的治安监控、交通管理、案件侦查等方面,GA/T 1400协议都发挥着重要作用。 以视频汇聚EasyCVR视频监控资源管理平台为例,该平台…...

【JavaScript脚本宇宙】瞬息万变:探索实时Web应用的JavaScript库
鸟瞰实时Web开发:JavaScript库大比拼 前言 随着Web应用程序的发展,实时通讯已成为一个重要的需求。本篇文章将探索六个关键的JavaScript库,这些库为我们提供助力,使得实时Web应用程序的创建成为可能。 欢迎订阅专栏:…...
)
Java数据结构与算法(有向无环图)
前言 有向无环图(Directed Graph)是在有向图的基础上,增加无环的检查。 实现原理 使用邻接表表示法实现有向图相对简单明了,步骤也相对简单。 1:首先创建有向图 2.创建顶点 3.顶点间创建边 4.创建边的过程中检查节点是否存…...

QuanTA: 一种新的高秩高效微调范式
QuanTA方法的核心是利用张量操作来模拟量子电路中的门操作。这些张量被设计为仅在特定的轴上应用,类似于量子电路中的单量子比特或双量子比特门。通过这种方式,QuanTA能够以高秩参数化来适应LLMs的权重矩阵。 网址:QuanTA: 一种新的高秩高效微…...

【漏洞复现】用友NC downCourseWare 任意文件读取漏洞
0x01 产品简介 用友NC是一款企业级ERP软件。作为一种信息化管理工具,用友NC提供了一系列业务管理模块,包括财务会计、采购管理、销售管理、物料管理、生产计划和人力资源管理等,帮助企业实现数字化转型和高效管理。 0x02 漏洞概述 用友NC …...

度安讲 | 第二期「安全左移·业务护航」技术沙龙成功举办
当下,“安全左移”作为落地DevSecOps的重要实践之一,已在业界达成共识。DevSecOps作为一种集开发、安全、运维于一体的软件开发和运营模式,强调在敏捷交付下,“安全”在软件开发生命周期的全覆盖贯穿和核心位置。所谓“安全左移”…...
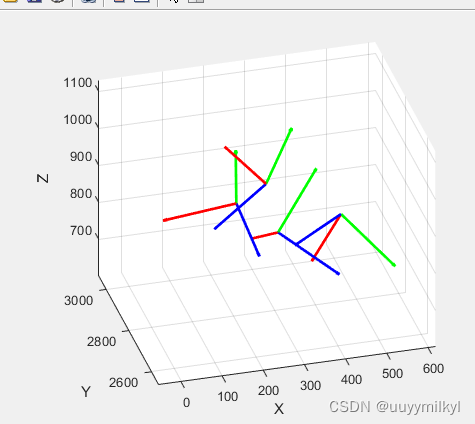
代码片段 | Matlab三维图显示[ R T 0 1] 的最佳方法
% 输入N组RT矩阵 N 4; R zeros(3, 3, N); T zeros(3, N); R(:,:,1) [-0.902608 0.250129 0.350335 ; 0.314198 0.939127 0.138996 ;-0.294242 0.235533 -0.926253 ]; T(:,1) [205.877;2796.02; 907.116];R(:,:,2) [-0.123936 0.643885 0.755018 ;0.816604 0.464468 -0.26…...
2024百度之星 跑步
原题链接:码题集OJ-跑步 题目大意:一个n个人在绕圈跑,第i个人跑一圈的时间是i分钟,每二个人位置相同就会打一次招呼,如果同时来到终点,他们就会停下来,请问会打多少次招呼? 思路&a…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...