数据挖掘与机器学习——聚类算法
目录
无监督学习
聚类算法
概念:
功能:
应用场景:
评判标准:
划分聚类:
K-means聚类
逻辑实现:
聚类方式
问题:
解决:
可能存在的问题:
1.初始值对K-means聚类的影响
2.K值对K-means聚类的影响
python实现:
层次聚类
凝聚层次聚类
分裂层次聚类
层次聚类运行过程
层次聚类的问题
解决办法
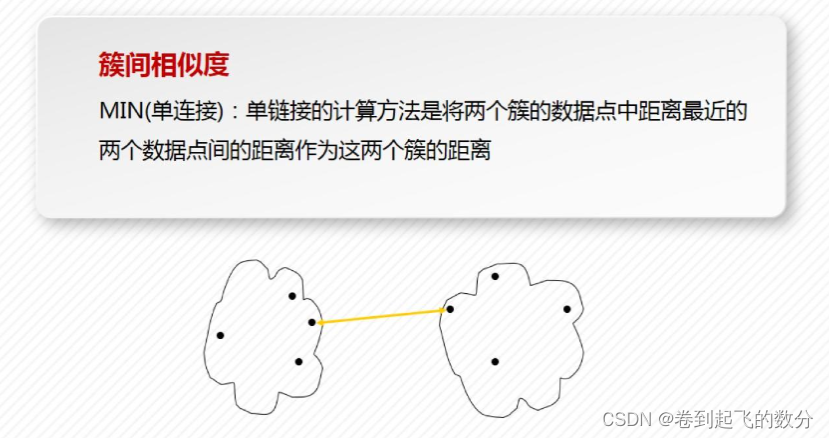
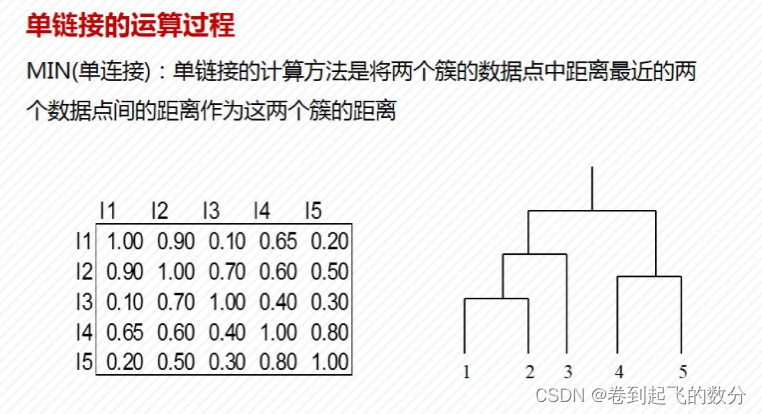
MIN单连接
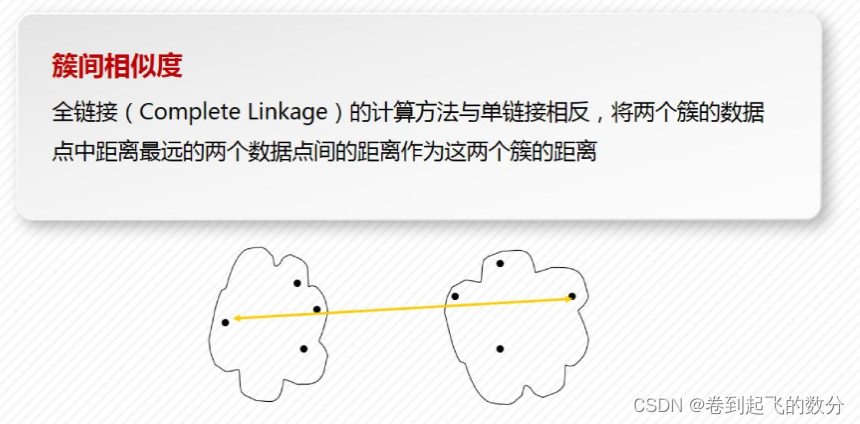
全连接
组平均
质心距离
层次聚类特点
python实现
密度聚类
相关概念
计算:
密度可达
密度相连
实现
优点:
缺点:
聚类质量衡量
轮廓系数
数据降维
特征选择实现方法:
代码实现:
特征提取实现方法
PCA算法
算法过程:
python实现:
无监督学习


聚类算法
概念:

功能:

应用场景:

评判标准:


划分聚类:


K-means聚类

逻辑实现:

聚类方式
问题:

解决:



可能存在的问题:
1.初始值对K-means聚类的影响

2.K值对K-means聚类的影响


python实现:

层次聚类


凝聚层次聚类


分裂层次聚类

层次聚类运行过程
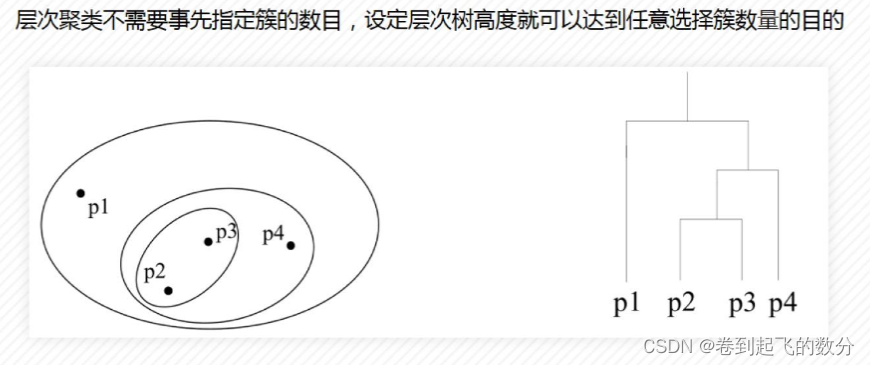
层次聚类的问题

解决办法

MIN单连接

全连接


组平均


质心距离


层次聚类特点

python实现

密度聚类

相关概念

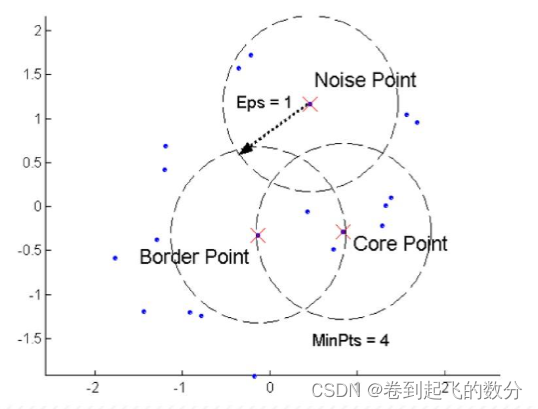
计算:

密度可达

密度相连

实现


优点:

缺点:

聚类质量衡量

轮廓系数


数据降维


特征选择实现方法:


代码实现:

特征提取实现方法


PCA算法


算法过程:


python实现:

相关文章:

数据挖掘与机器学习——聚类算法
目录 无监督学习 聚类算法 概念: 功能: 应用场景: 评判标准: 划分聚类: K-means聚类 逻辑实现: 聚类方式 问题: 解决: 可能存在的问题: 1.初始值对K-means聚…...
QT快速下载
去QT官网之后,如下图所示 比如要下载qt-opensource-windows-x86-5.14.2.exe,进入5.14对应的文件夹,找到对应的版本 点击Details, 下载对应的种子,然后通过迅雷下载 个人实测,家庭网络平均18M的速率...

最短路问题
最短路问题是图论里非常经典的一个考点 接下来着重讲述五种求最短路的算法:朴素版dijkstra算法、堆优化版的dijkstra算法、bellman-ford算法、spfa算法、floyd算法 总体思维导图: 总体思路: 最短路分为两大类 { 在以下给出的时间复杂度中n…...

spark MLlib 中的分类模型
理解这些机器学习模型的数学原理需要一定的数学基础,下面我将简要介绍每个模型的数学原理,并附上相关的数学公式。 1. LinearSVC(线性支持向量机) 数学原理: 线性支持向量机的目标是找到一个超平面,最大化…...

24上半年报考人数“不增反降”?备考下半年软考的难了......
近日,工信教考发布了一篇《2024年上半年计算机软件资格考试顺利举行》的文章,公布了2024年上半年软考报考人数共计52.77万人,其中,初级资格5.12万人、中级资格24.37万人、高级资格23.28万人。 软考高级占总报名人数的44%…...
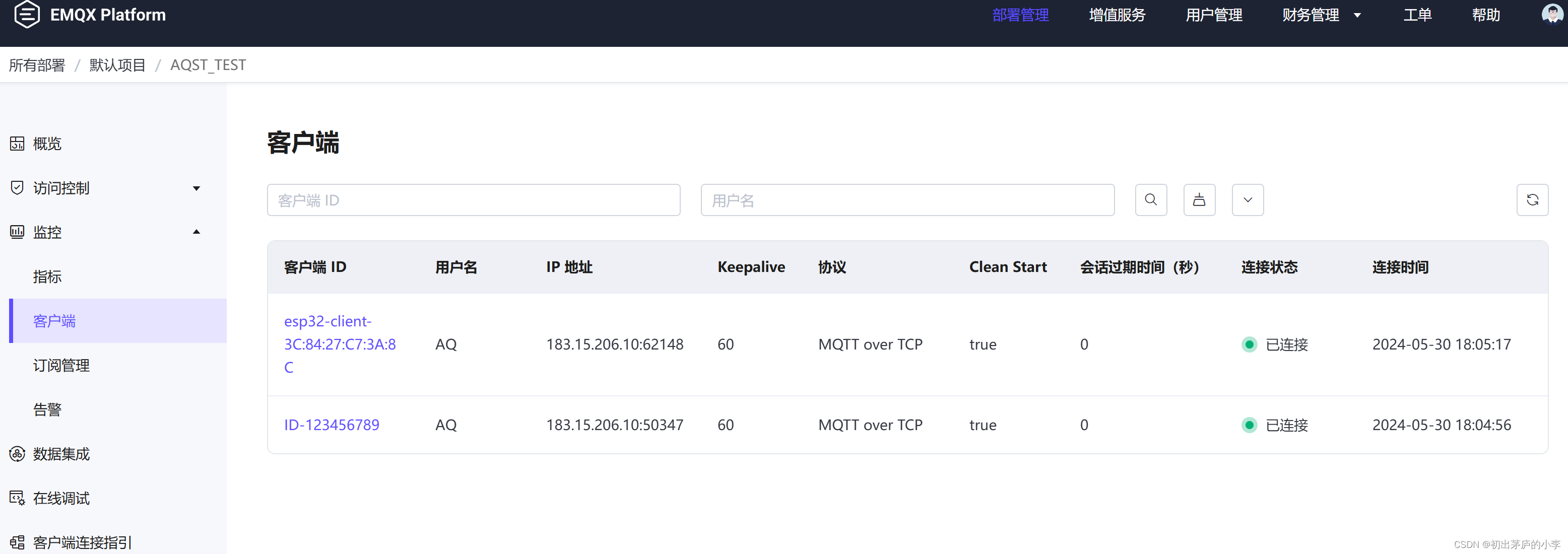
初出茅庐的小李博客之使用立创开发板(ESP32)连接到EMQX Platform【MQTT TLS/SSL 端口连接】
介绍 手上有一块立创开发板,本着不吃灰的原则把它用起来,今天就来用它来连接上自己部署的MQTT服务器进行数据通信。 硬件:立创开发板 开发环境:Arduino IDE Win11 MQTT 平台:EMQX Platform 立创开发板介绍࿱…...

js平滑滚动元素使其可见
直接上重点: let xpath "//*/div[idxxx]"; document.evaluate(xpath, document, null, XPathResult.FIRST_ORDERED_NODE_TYPE, null).singleNodeValue.scrollIntoView({ behavior: "smooth"})这段代码是JavaScript中使用XPath查询文档并执行平…...

TP6 事件绑定、监听、订阅
事件绑定与监听 命令行生成事件类 php think make:event EventDemo 命令行生成事件监听类php think make:listener ListenerDemo 事件类可作为保存与事件相关信息的容器,如没有额外需求可以不需要定义 事件系统的所有操作都通过think\facade\Event类进行静态调用 当定义…...

SpringCloud Gateway中Filters详细说明
前面 https://blog.csdn.net/J080624/article/details/139494909 我们研究了GateWay中各种路由断言的使用。SpringCloud GateWay 还提供了各种过滤器用来对请求和响应进行处理。 官网地址:SpringCloud Gateway Filter 【1】GatewayFilter Factories 路由过滤器允…...

力扣2156.查找给定哈希值的子串
力扣2156.查找给定哈希值的子串 rolling hash:求带权的值 左边是高位 右边是低位 本题要求左边低位 只要反向求即可 class Solution {public:string subStrHash(string s, int power, int modulo, int k, int hashValue) {int n s.size();long long M modulo,p…...
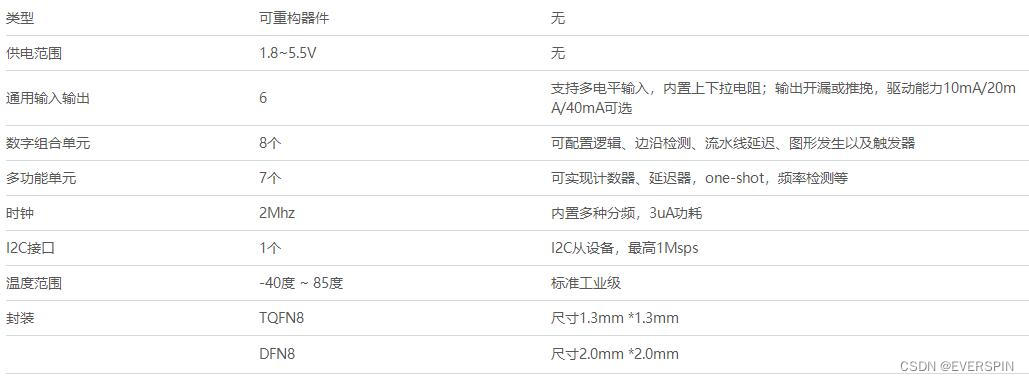
推荐低成本低功耗的纯数字现场可重构IC
CPLD采用CMOS EPROM、EEPROM、快闪存储器和SRAM等编程技术,从而构成了高密度、高速度和低功耗的可编程逻辑器件。 RAMSUN提供的型号LS98003是通用可配置的数字逻辑芯片,有体积小、超低功耗和高可靠性等特点。客户可以根据自己的功能需求设计芯片&#x…...

解决change事件与blur事件互不影响
<template><div style"margin-top: 40px"><el-selectv-model"form.name"placeholder"请选择名称"clearablefilterableref"selectName"allow-createblur"nameBlur($event)"visible-change"visibleNameCh…...

后端开发面经系列 -- 同程旅行C++一面
同程旅行C一面 公众号:阿Q技术站 文章目录 同程旅行C一面1、sizeof与strlen的区别?2、运算符和函数有什么区别?3、new和malloc?4、内存泄漏与规避方法?5、悬空指针与野指针?6、手撕冒泡排序?7、…...

推荐几个开源的c#的工作流引擎组件
以下是一个.NET Core领域可以推荐使用的流程引擎的表格: 名称 生产厂家 下载地址 支持二开 独立部署 ccflow 济南驰骋信息技术有限公司 https://gitee.com/opencc 是 是 Elsa Elsa Workflows GitHub - elsa-workflows/elsa-core: A .NET workflows li…...
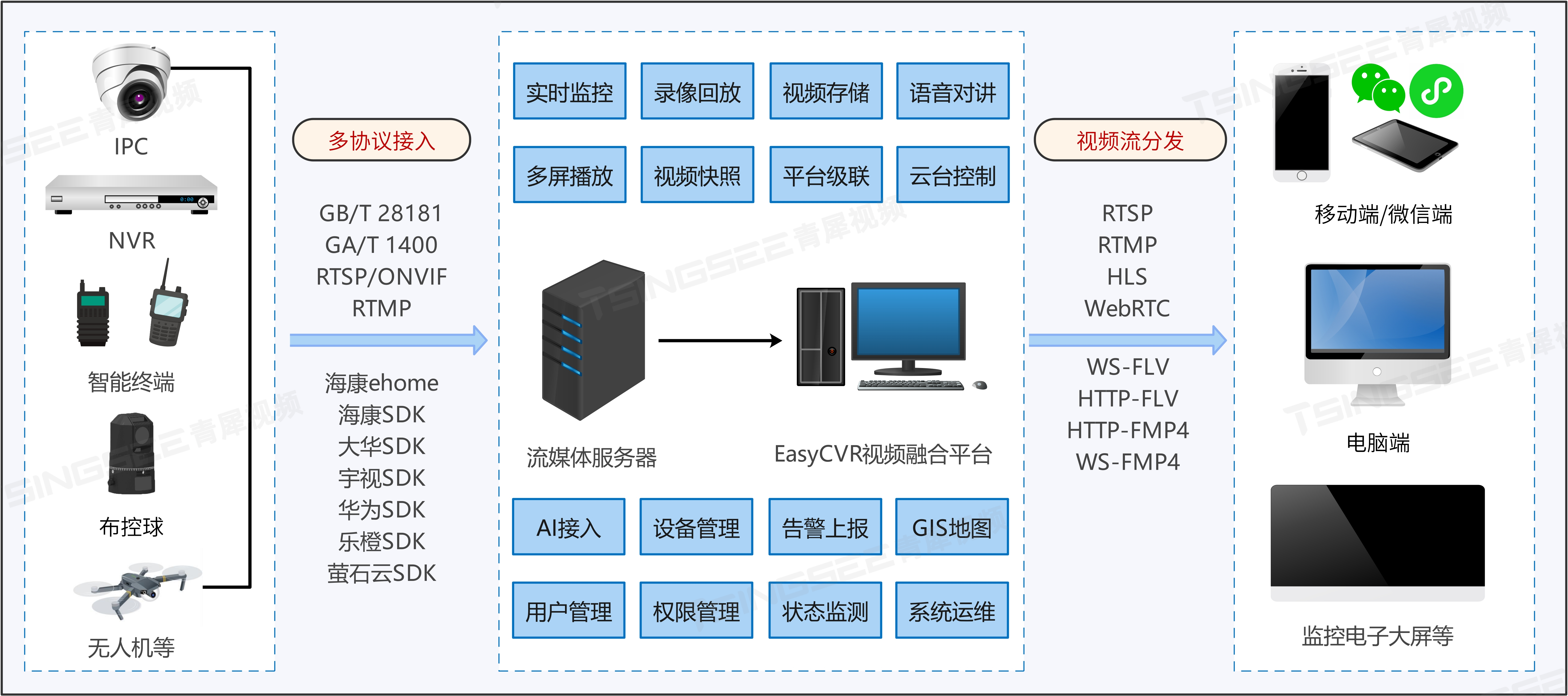
视频汇聚EasyCVR视频监控云平台对接GA/T 1400视图库对象和对象集合XMLSchema描述
GA/T 1400协议主要应用于公安系统的视频图像信息应用系统,如警务综合平台、治安防控系统、交通管理系统等。在城市的治安监控、交通管理、案件侦查等方面,GA/T 1400协议都发挥着重要作用。 以视频汇聚EasyCVR视频监控资源管理平台为例,该平台…...

【JavaScript脚本宇宙】瞬息万变:探索实时Web应用的JavaScript库
鸟瞰实时Web开发:JavaScript库大比拼 前言 随着Web应用程序的发展,实时通讯已成为一个重要的需求。本篇文章将探索六个关键的JavaScript库,这些库为我们提供助力,使得实时Web应用程序的创建成为可能。 欢迎订阅专栏:…...
)
Java数据结构与算法(有向无环图)
前言 有向无环图(Directed Graph)是在有向图的基础上,增加无环的检查。 实现原理 使用邻接表表示法实现有向图相对简单明了,步骤也相对简单。 1:首先创建有向图 2.创建顶点 3.顶点间创建边 4.创建边的过程中检查节点是否存…...

QuanTA: 一种新的高秩高效微调范式
QuanTA方法的核心是利用张量操作来模拟量子电路中的门操作。这些张量被设计为仅在特定的轴上应用,类似于量子电路中的单量子比特或双量子比特门。通过这种方式,QuanTA能够以高秩参数化来适应LLMs的权重矩阵。 网址:QuanTA: 一种新的高秩高效微…...

【漏洞复现】用友NC downCourseWare 任意文件读取漏洞
0x01 产品简介 用友NC是一款企业级ERP软件。作为一种信息化管理工具,用友NC提供了一系列业务管理模块,包括财务会计、采购管理、销售管理、物料管理、生产计划和人力资源管理等,帮助企业实现数字化转型和高效管理。 0x02 漏洞概述 用友NC …...

度安讲 | 第二期「安全左移·业务护航」技术沙龙成功举办
当下,“安全左移”作为落地DevSecOps的重要实践之一,已在业界达成共识。DevSecOps作为一种集开发、安全、运维于一体的软件开发和运营模式,强调在敏捷交付下,“安全”在软件开发生命周期的全覆盖贯穿和核心位置。所谓“安全左移”…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
