动态规划(多重背包问题+二进制优化)
引言
多重背包,相对于01背包来说,多重背包是每个物品会有相应的个数,最多可以选那么多个,因而对于朴素多重背包,需要在01背包的基础上,再加一层物品的循环
朴素多重背包例题
P2347 [NOIP1996 提高组] 砝码称重

题意,就是说有六种砝码每种砝码有自己的个数,问你能达到的重量搭配是多少
题解:标准的多重背包,我们可以用dp[ j ]去表示 j 重量能否达到,如果能达到就是1,如果不能打达到就是0,最后遍历一遍dp数组去判断有多少个1即可
#include<bits/stdc++.h>
using namespace std;
int a[7];
int w[7]={0,1,2,3,5,10,20};
int dp[1050];int main()
{for(int i=1;i<=6;i++)cin>>a[i];dp[0]=1;for(int i=1;i<=6;i++){for(int j=1050;j>=0;j--){for(int k=0;k<=a[i];k++)//遍历第i个物品选的个数{if(dp[j]==1){dp[j+k*w[i]]=1;}}}}int sum=0;for(int i=1;i<=1000;i++)if(dp[i]!=0)sum++;cout<<"Total="<<sum;return 0;
}P6771 [USACO05MAR] Space Elevator 太空电梯
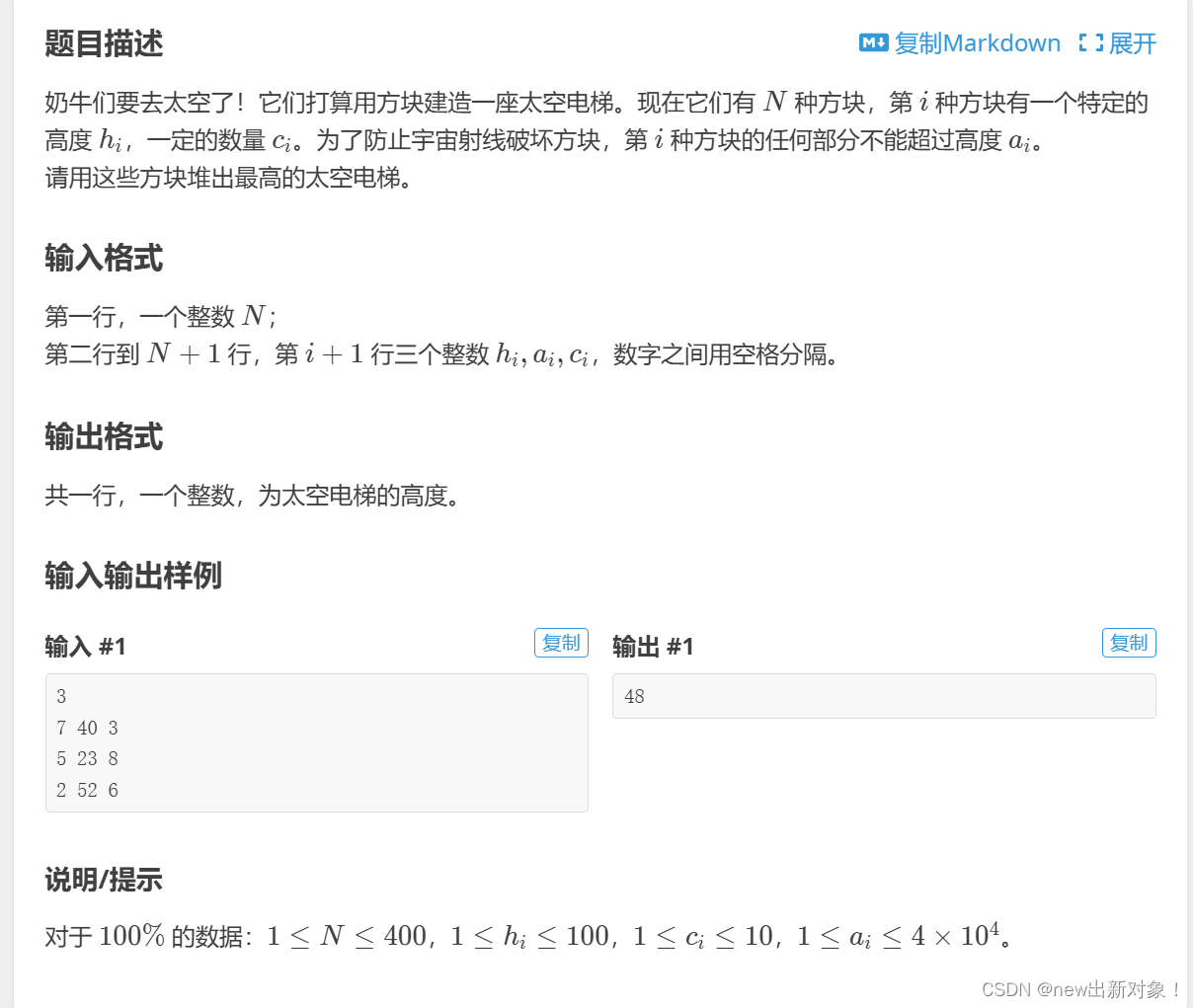
题意,就是说给你n中方块,每个方块有自己的高度,和最大搭建的限制(在某个高度以后不能用这种方块),还有方块的数量
思路:这是一个变式,我们需要将其组装成一个结构体,然后对a数组进行排序,从小到大进行排序,然后进行多重背包即可
#include<bits/stdc++.h>
using namespace std;
int n;
struct node{int h;int limit;int num;
}a[405];
int dp[40005];//能否达到高度为j,能达到为1,不能为0bool cmp(node a,node b)
{return a.limit<b.limit;
}int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i].h>>a[i].limit>>a[i].num;dp[0]=1;sort(a+1,a+1+n,cmp);for(int i=1;i<=n;i++){for(int j=a[i].limit;j>=0;j--){for(int k=0;k<=a[i].num&&j+k*a[i].h<=a[i].limit;k++){if(dp[j]==1){dp[j+k*a[i].h]=1;}}}}for(int i=a[n].limit;i>=0;i--){if(dp[i]==1){cout<<i;return 0;}}return 0;
} P5365 [SNOI2017] 英雄联盟

题意:有n个英雄,每个英雄有k个皮肤,对于一个英雄的所有皮肤都是一个价格c,但是我又想要m中搭配,正常的求法是算出m个搭配至少要多少钱,但是这题m的数据太大了,只能通过对于一定的钱,其搭配数是多少
思路:dp数组表示的是对于j元,总共有多少的搭配数,然后判断这个搭配数是否大于m从前向后遍历,找到第一个大于m种搭配的位置,那个下标就是最小花费
//英雄联盟
//这题皮肤搭配数量太大了,肯定不能当数组,要换成j个q币能搞得最大皮肤搭配
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int num[135];
int w[135];
int dp[270005];
signed main()
{cin>>n>>m;int sum=0;//计算总金额 for(int i=1;i<=n;i++){cin>>num[i];}for(int i=1;i<=n;i++){cin>>w[i];sum+=num[i]*w[i];}dp[0]=1;for(int i=1;i<=n;i++){for(int j=sum;j>=0;j--){for(int k=0;k<=num[i]&&k*w[i]<=j;k++){dp[j]=max(dp[j],dp[j-k*w[i]]*k);}}}for(int i=1;i<=sum;i++){if(dp[i]>=m){cout<<i;return 0;}}return 0;
}二进制优化
用到的是二进制拆分思想
比如说对于50这个数,我们用二进制拆分可以分为 1,2,4,8,16,19,这五个数,我们这五个数搭配可以组成50以内的所有自然数,所以我们二进制优化也是通过拆分每个物品的个数从而降低时间复杂度,从而形成完全的01背包问题
二进制优化例题
P1776 宝物筛选

一看这道题,如果用正常的多重背包,时间复杂度为100*40000*100000肯定会爆数据的,所以我们要用二进制优化,将时间复杂度变为4e6*log2(100000),这样就大大降低的时间的复杂度
将物品数量进行二进制拆分
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int v[1405];
int w[1405];
int dp[40005];signed main()
{cin>>n>>m;int vv,ww,mm;int cnt=0;for(int i=1;i<=n;i++){cin>>vv>>ww>>mm;for(int j=1;j<=mm;j<<=1){cnt++;v[cnt]=j*vv;w[cnt]=j*ww;mm-=j;}if(mm){cnt++;v[cnt]=mm*vv;w[cnt]=mm*ww;}}for(int i=1;i<=cnt;i++){for(int j=m;j>=w[i];j--){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}cout<<dp[m];return 0;
}
相关文章:

动态规划(多重背包问题+二进制优化)
引言 多重背包,相对于01背包来说,多重背包是每个物品会有相应的个数,最多可以选那么多个,因而对于朴素多重背包,需要在01背包的基础上,再加一层物品的循环 朴素多重背包例题 P2347 [NOIP1996 提高组] 砝…...

AI学习指南机器学习篇-逻辑回归正则化技术
AI学习指南机器学习篇-逻辑回归正则化技术 在机器学习领域,逻辑回归是一种常见的分类算法,它常用于处理二分类问题。在实际的应用中,为了提高模型的泛化能力和降低过拟合风险,逻辑回归算法通常会使用正则化技术。本文将介绍逻辑回…...

Django按照文章ID删除文章
重点是‘文章的ID’作为参数,如何在各个部分传递。 1、在视图函数部分 login_required def article_list(request):articles ArticlePost.objects.filter(authorrequest.user)context {articles: articles, }return render(request, article/column/article_lis…...

Java | Leetcode Java题解之第136题只出现一次的数字
题目: 题解: class Solution {public int singleNumber(int[] nums) {int single 0;for (int num : nums) {single ^ num;}return single;} }...
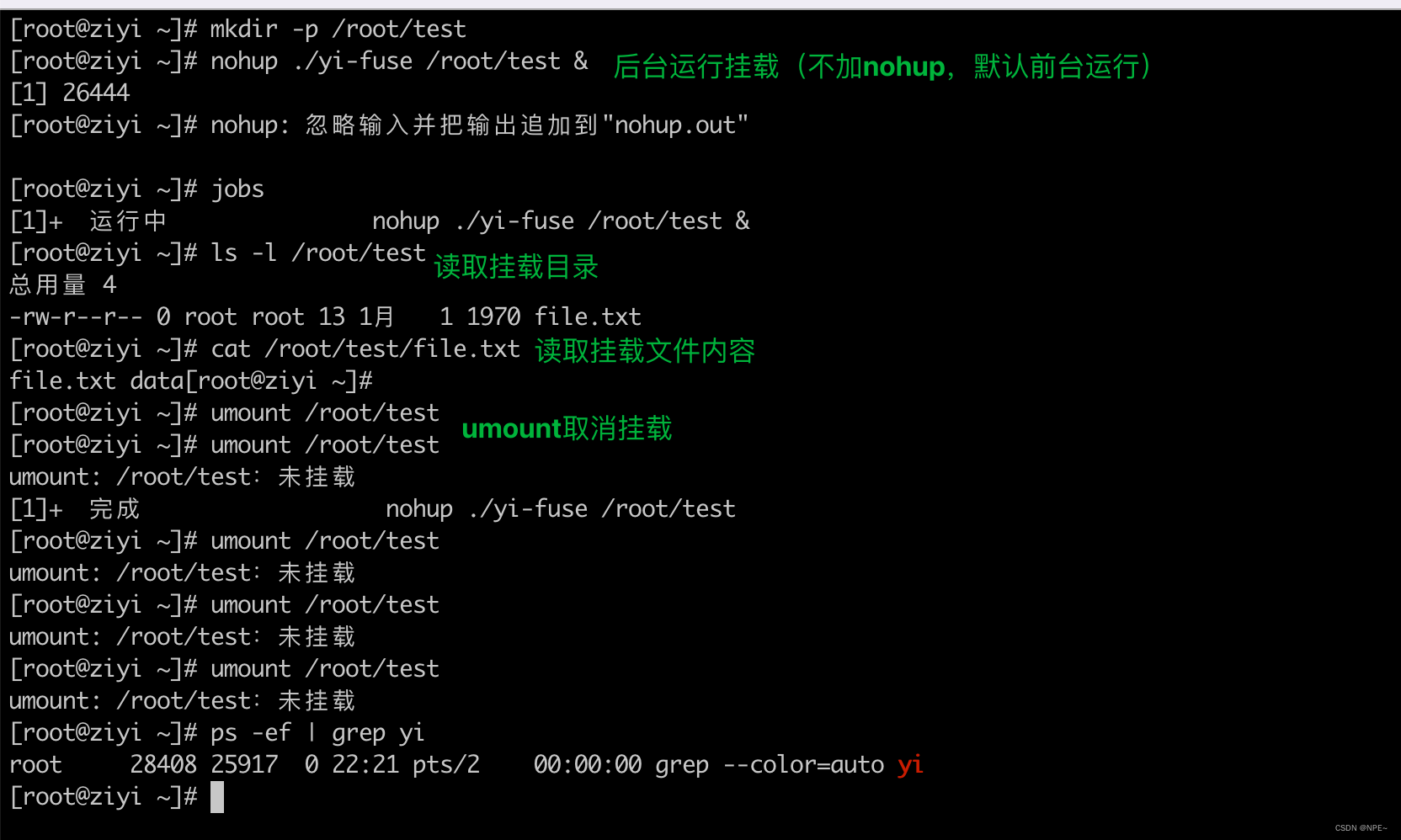
文件系统小册(FusePosixK8s csi)【1 Fuse】
文件系统小册(Fuse&Posix&K8s csi)【1 Fuse:用户空间的文件系统】 Fuse(filesystem in userspace),是一个用户空间的文件系统。通过fuse内核模块的支持,开发者只需要根据fuse提供的接口实现具体的文件操作就可以实现一个文…...

Bootstrap 环境安装
Bootstrap 环境安装 Bootstrap 是一个流行的前端框架,用于快速开发响应式和移动设备优先的网站。在开始使用 Bootstrap 之前,您需要安装相应的环境。本文将指导您如何安装 Bootstrap 环境。 1. 环境要求 在开始之前,请确保您的计算机上已安装以下软件: Node.js:Bootstr…...

GWT 与 Python App Engine 集成
将 Google Web Toolkit (GWT) 与 Python App Engine 集成可以实现强大的 Web 应用程序开发。这种集成允许你使用 GWT 的 Java 客户端技术构建丰富的用户界面,并将其与 Python 后端结合在一起,后端可以运行在 Google App Engine 上。 1、问题背景 在 Pyt…...

golang的函数为什么能有多个返回值?
在golang1.17之前,函数的参数和返回值都是放在函数栈里面的,比如函数A调用函数B,那么B的实参和返回值都是存放在函数A的栈里面,所以可以轻松的返回多个值。 其他的编程语言大都使用某个寄存器来存储函数的返回值。 但是从golang…...

一次 K8s 故障诊断:从 CPU 高负载到存储挂载泄露根源揭示
一、背景 现代软件部署中,容器技术已成为不可或缺的一环,在云计算和微服务架构中发挥着核心作用。随着容器化应用的普及,确保容器环境的可靠性成为了一个至关重要的任务。这就是容器SRE(Site Reliability Engineering,…...
)
python大作业:实现的简易股票简易系统(含源码、说明和运行截图)
实现一个简单的股票交易模拟系统。该系统将包括以下几个部分: 数据处理:从CSV文件中读取股票数据。 股票交易算法:实现一个简单的交易策略。 命令行界面(CLI):允许用户查看股票数据和进行交易。 数据持久化:将用户的交易记录和当前资金存储在数据库中。 为了简化这个示例…...

python-NLP常用数据集0.1.012
XNLI数据集 用户语言翻译和跨语言分类的语料库 官网地址:https://github.com/facebookresearch/XNLI下载地址:https://dl.fbaipublicfiles.com/XNLI/XNLI-1.0.zip注意事项:数据集有json格式的,和txt格式的数据格式 txt格式 la…...
【大事件】docker可能无法使用了
今天本想继续学习docker的命令,突然发现官方网站的文档页面打不开了。 难道是被墙了? 我用同事的翻了一下,能进,果然! 正好手头的工作告一段落,将代码上传,然后通过jenkins将服务器自动部署到…...

探索Linux中的gzip命令:压缩与解压缩的艺术
探索Linux中的gzip命令:压缩与解压缩的艺术 在Linux世界中,文件压缩和解压缩是日常任务中不可或缺的一部分。gzip命令是这些任务中的佼佼者,它提供了高效的压缩和解压缩功能,广泛应用于各种场景。本文将带您深入了解gzip命令的工…...

Shell 输入/输出重定向
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 💝Ὁ…...

为什么RPC要比Http高效?
RPC和HTTP RPC(Remote Procedure Call)基于TCP连接通常比HTTP在性能上要高很多,原因如下: 1. 协议开销 HTTP开销: HTTP协议报文头部相对较大,包含大量的元数据(如方法、URI、头字段等&#x…...

局域网电脑监控软件是如何监控到内网电脑的?
在信息化快速发展的今天,局域网电脑监控软件成为许多企业、学校和机构重要的实用工具。这些软件的主要功能在于对局域网内的电脑进行实时监控,以确保网络的安全、员工的工作效率以及合规性。那么,局域网电脑监控软件是如何做到对内网电脑进行…...
精妙无比的App UI 风格
精妙无比的App UI 风格...

SQL优化系列-快速学会分析SQL执行效率(下)
1 show profile 分析慢查询 有时需要确定 SQL 到底慢在哪个环节,此时 explain 可能不好确定。在 MySQL 数据库中,通过 profile,能够更清楚地了解 SQL 执行过程的资源使用情况,能让我们知道到底慢在哪个环节。 知识扩展࿱…...

交流非线性RCD负载的核心功能
非线性RCD负载是一种广泛应用于电力系统中的电子元件,主要用于保护电路免受过电压和欠电压的影响。它的核心功能主要包括以下几个方面: 1. 过电压保护:当电路中的电压超过设定值时,非线性RCD负载会自动断开电路,防止电…...

英语学习笔记31——Where‘s Sally?
Where’s Sally? Sally在哪? 词汇 Vocabulary garden /ˈɡɑːrdn/ n. 花园,院子(属于私人) 区别:park n. 公园(公共的) 例句:我的花园非常大。 My garden is very big. 搭…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
