MATLAB基础应用精讲-【数模应用】二元Logit分析（最终篇）（附python、MATLAB和R语言代码实现）
目录
算法原理
SPSSAU
1、二元logistic分析思路说明
2、如何使用SPSSAU进行二元logistic操作
3、二元logistic相关问题
算法流程
一、分析前准备
1、确定分析项
2．多重共线性判断
3．数据预处理
二、回归基本情况分析
三、模型拟合评价
1、似然比检验
2、拟合优度检验
四、回归分析结果解读
1．R方值分析
2．模型公式
3．X对Y影响情况分析
4．OR值说明
五、模型预测能力分析
六、边际效应结果说明
应用案例
1.案例背景与分析策略
1.1 案例背景介绍
1.2 明确目的与分析策略
2.数据预处理
2.1 因变量重新数据编码
2.2 分类自变量哑变量转换
3.单因素分析
3.1 针对分类自变量的卡方检验
3.2 针对连续自变量的t检验
4.多因素logistic回归模型
4.1 逐步回归
4.2 模型拟合评价
4.3 模型预测能力
代码实现
R语言
Python
MATLAB
算法原理
SPSSAU
在研究X对于Y的影响时，如果Y为定量数据，那么使用多元线性回归分析（SPSSAU通用方法里面的线性回归）；如果Y为定类数据，那么使用Logistic回归分析。
结合实际情况，可以将Logistic回归分析分为3类，分别是二元Logistic回归分析、多元有序Logistic回归分析和多元无序Logistic回归分析，如下图。
Logistic回归分析用于研究X对Y的影响，并且对X的数据类型没有要求，X可以为定类数据，也可以为定量数据，但要求Y必须为定类数据，并且根据Y的选项数，使用相应的数据分析方法。
1、二元logistic分析思路说明
在进行二元Logistic回归分析时，通常会涉及3个步骤，分别是数据
相关文章：
MATLAB基础应用精讲-【数模应用】二元Logit分析（最终篇）（附python、MATLAB和R语言代码实现）
目录 算法原理 SPSSAU 1、二元logistic分析思路说明 2、如何使用SPSSAU进行二元logistic操作 3、二元logistic相关问题 算法流程 一、分析前准备 1、确定分析项 2．多重共线性判断 3．数据预处理 二、回归基本情况分析 三、模型拟合评价 1、似然比检验 2、拟合优…...
centos7安装mysql（完整）
官网5.7版本：https://cdn.mysql.com//Downloads/MySQL-5.7/mysql-5.7.29-1.el7.x86_64.rpm-bundle.tar 文件存于百度网盘：链接：https://pan.baidu.com/s/1x0fucIsD36_7agu88Jd2yg 提取码：s4m8 复制这段内容后打开百度网盘手机A…...
C++ STL std::vector的实现机制【面试】
std::vector 是 C 标准模板库（STL）中的一种序列容器，它封装了动态数组的实现，提供了一系列方法来操作这个动态数组。以下是 std::vector 的一些关键实现机制： 连续内存存储： std::vector 通过一块连续的内存…...
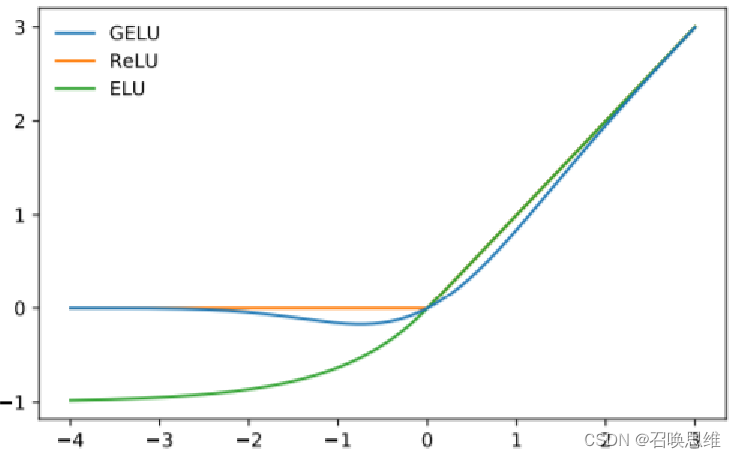
激活函数对比
激活函数 sigmoid / tanh / relu / leaky relu / elu / gelu / swish 1、sigmoid 优缺点 1) 均值!0，导致fwxb求导时，方向要么全正要么全负 可以通过batch批量训练来缓解 2) 输入值大于一定范围梯度就会消失 3) 运算复杂 2、tanh 优缺点 1) 均值0 2)…...
pycharm 上一次编辑位置不见了
目录 pycharm2024版 上一次编辑位置不见了，研究发现移到了左下角了，如下图所示： 上一次编辑位置快捷键： 设置为旧版ui，新版不好用 pycharm2024版 上一次编辑位置不见了，研究发现移到了左下角了ÿ…...
FFmpeg播放器的相关概念【1】
播放器框架 相关术语 •容器／文件（Conainer/File）：即特定格式的多媒体文件，比如mp4、flv、mkv等。 • 媒体流（Stream）：表示时间轴上的一段连续数据，如一段声音数据、一段…...
=与==的优先级
项目场景： 在写消息队列的过程中，问题代码如下： #include "message.h"void send(message *msg, int msg_id); void main() {printf("The sender process id %d\n", getpid());key_t key;int msg_id;message msg {.ty…...
在Linux上的Java项目导出PDF乱码问题
在Linux上的Java项目导出PDF乱码问题 场景：一个Java项目导出PDF，在我本地导出是没有问题，但是部署上Linux上后，导出就出现了乱码了。 处理方案 我这里使用的处理方案是在Linux服务器上安装一些PDF需要使用的字体 1.把字体上传到…...
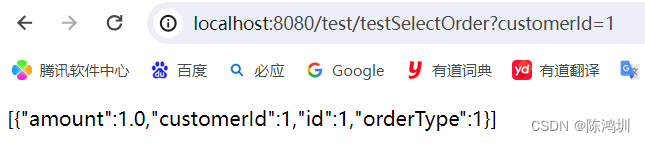
java：使用shardingSphere访问mysql的分库分表数据
# 创建分库与分表 创建两个数据库【order_db_1、order_db_2】。 然后在两个数据库下分别创建三个表【orders_1、orders_2、orders_3】。 建表sql请参考： CREATE TABLE orders_1 (id bigint NOT NULL,order_type varchar(255) NULL DEFAULT NULL,customer_id bigi…...
红酒：如何选择适合的红酒储存容器
选择适合的红酒储存容器对于保持雷盛红酒的品质和风味至关重要。不同的容器具有不同的优缺点，因此应根据个人需求和条件进行选择。以下是一些常见的红酒储存容器的特点和适用场景： 玻璃瓶：玻璃瓶是常见的红酒储存容器。它具有良好的密封性能、…...
【C++】 使用CRT 库检测内存泄漏
CRT 库检测内存泄漏 一、CRT 库简介二、CRT 库的使用1、启用内存泄漏检测2、设置应用退出时显示内存泄漏报告3、丰富内存泄漏报告4、演示使用 内存泄漏是 C/C 应用程序中最微妙、最难以发现的 bug，存泄漏是由于之前分配的内存未能正确解除分配而导致的。 最开始的少…...
python手动搭建transformer，并实现自回归推理
以下是添加了详细注释的代码和参数介绍： Transformer 实现及自回归推理 本文展示了如何手动实现一个简化版的Transformer模型，并用自回归方式实现一个seq2seq任务，例如机器翻译。 导入必要的库 import torch import torch.nn as nn import…...
AI数据分析：用deepseek进行贡献度分析(帕累托法则)
帕累托法则，也称为80/20法则，是由意大利经济学家维尔弗雷多帕累托提出的。它指出在许多情况下，大约80%的效益来自于20%的原因。这个原则在很多领域都有应用，包括商业、经济、社会问题等。 在数据分析中，帕累托法则可以…...
生成式人工智能的风险与治理——以ChatGPT为例
文 | 西南政法大学经济法学院 马羽男 以ChatGPT为代表的生成式人工智能在创造社会福利的同时，也带来了诸多风险。因此，当务之急是结合我国生成式人工智能发展状况，厘清其应用价值与潜在风险之间的关系，以便在不影响应用发展的前提…...
十足正式在山东开疆拓土！首批店7月初开业，地区便利店现全新面貌！
十足便利店将正式进军山东市场，以济南、淄博两座城市为核心发展起点，目前济南市已经有三家十足门店正在装修施工中，首批15家门店将于7月初开业，这标志着十足集团市场战略布局迈出了至关重要的一步。 随着3月份罗森品牌在济南成功开…...
Unity2D游戏开发-玩家控制
在Unity2D游戏开发中，玩家控制是游戏互动性的核心。本文将解析一个典型的Unity2D玩家控制脚本，探讨如何实现流畅的玩家移动、跳跃和动画切换。以下是一个Unity脚本示例，实现了这些基础功能。 1. 脚本结构 using System.Collections; using …...
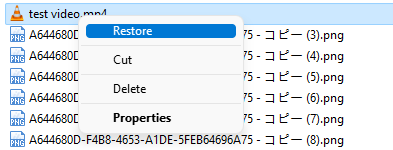
如何在 Windows 11 上免费恢复永久删除的文件
虽然Windows 上的已删除文件恢复不简单，但您可能希望免费或无需任何软件即可恢复已删除的文件。下面，我们列出了一个指南，其中包含有关如何在 Windows 11 上免费检索永久删除的文件的说明。 #1 奇客数据恢复 奇客数据恢复是一个广受好评的免…...
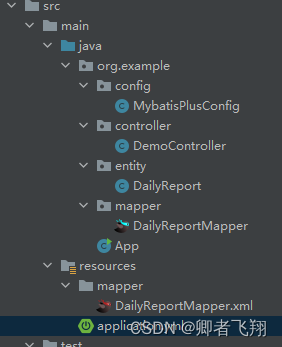
Spring boot 集成mybatis-plus
Spring boot 集成mybatis-plus 背景 Spring boot集成mybatis后，我们可以使用mybatis来操作数据。然后，我们还是需要写许多重复的代码和sql语句，比如增删改查。这时候，我们就可以使用 mybatis-plus了，它可以极大解放我…...
数据仓库之缓慢变化维
缓慢变化维（Slowly Changing Dimensions, SCD）是数据仓库设计中的一个重要概念，用于处理维度表中随时间缓慢变化的属性。维度表中的数据通常描述业务实体（如客户、产品、员工等），而这些实体的某些属性&…...
跑mask2former（自用）
1. 运行docker 基本命令： sudo docker ps -a （列出所有容器状态） sudo docker run -dit -v /hdd/lyh/mask2former:/mask --gpus "device0,1" --shm-size 16G --name mask 11.1:v6 （创建docker容器&…...
React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook，用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途，下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes（简称K8s）中，Ingress是一个API对象，它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress，你可…...
3.3.1_1 检错编码（奇偶校验码）
从这节课开始，我们会探讨数据链路层的差错控制功能，差错控制功能的主要目标是要发现并且解决一个帧内部的位错误，我们需要使用特殊的编码技术去发现帧内部的位错误，当我们发现位错误之后，通常来说有两种解决方案。第一…...
UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法：netstat [选项] 功能：查看网络状态 常用选项： n 拒绝显示别名&#…...
MVC 数据库
MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）
【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...
Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库，例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体，比如 SnowballFight、Huggy the Do…...
3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象，只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意：它移动的位置必须是相连的有内容的单元格…...
华硕a豆14 Air香氛版，美学与科技的馨香融合
在快节奏的现代生活中，我们渴望一个能激发创想、愉悦感官的工作与生活伙伴，它不仅是冰冷的科技工具，更能触动我们内心深处的细腻情感。正是在这样的期许下，华硕a豆14 Air香氛版翩然而至，它以一种前所未有的方式&#x…...