LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划
LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划
文章目录
- LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划
- 前言
- 一、题目概述
- 二、解题方法
- 2.1 一维表格的自底向上动态规划
- 2.1.1 思路讲解
- 2.1.2 伪代码 + 逐步输出示例
- 2.1.3 Python代码如下
- 2.1.4 C++代码如下
- 2.2 二维表格的自底向上动态规划
- 2.2.1 思路讲解
- 2.2.2 伪代码 + 逐步输出示例
- 2.2.3 Python代码如下
- 2.2.4 C++代码如下
- 2.3 方法对比
- 三、英语词汇
前言
LeetCode位置:416. 分割等和子集
日常刷题,维持手感,同步学习英语,刷题顺序参考B站UP@justyyuk的系列视频,感兴趣的点波关注。
学海无涯,大路千万,感恩此程,彼此真诚陪伴!
Ps:第一次刷到的道友留步,这里拉齐一下信息。文章主要记录视频中的主要内容,算法思路会按照个人理解,用伪代码+举例每步输出的方式呈现。代码部分会以Python和C++语法进行呈现。文章最后会总结一些英语词汇。OK,就啰嗦这么多,开始进步[干杯🐱👓]
一、题目概述

输入:nums列表
输出:bool值,表示原始列表是否存在和相等的两个子列表
PS:
子序列 (Subsequence/Subset):
- 子序列是通过从原始序列中删除一些或不删除任何元素且不改变剩余元素顺序而得到的序列。
- 例子:对于序列 [1, 2, 3, 4],[1, 3, 4] 和 [2, 4] 是子序列。
- 注意:[1, 4, 3] 不是 子序列,因为顺序改变了。
子列表 (Sublist)
- 子列表是列表的连续部分,意味着元素必须是连续的。
- 例子:对于列表 [1, 2, 3, 4],[2, 3] 和 [1, 2, 3]是子列表。
- 注意:[1, 3] 不是 子列表,因为它不是连续的。
子数组 (Subarray):
- 类似于子列表,子数组是数组的连续部分。
- 例子:对于数组 [1, 2, 3, 4],[2, 3] 和 [1, 2, 3] 是子数组。
- 注意:[1, 3] 不是 子数组,因为它不是连续的。
- 在许多情况下,当数据结构是数组或列表时,“子列表”和“子数组”可以互换使用,但“子数组”一词专门用于数组。
二、解题方法
2.1 一维表格的自底向上动态规划
2.1.1 思路讲解
动态规划策略 :
本题与昨天的是同一道题,不过这次采用自底向上(表格法)的动态规划策略。此处有两种方法,一种使用到一维表格,一种使用二维表格。
一维表格:用表格长度表示待达成目标,即数组和的一半(+1),表格内的值(True/False)表示子序列是否选择当前元素
- 表格长度:表格 dp 的长度为 half + 1,其中 half 是数组总和的一半。这意味着我们试图判断是否存在一个子集,使其和为 0 到 half 之间的任何值。
- 表格的值:dp[i] 是一个布尔值,表示是否存在一个子集,其和等于 i。
- 初始化:dp[0] 被初始化为 True,因为和为 0 的子集总是存在的(空集)。其他位置被初始化为 False。
- 状态转移:
- 对于数组中的每一个元素 num,从后向前遍历 dp 数组(从 half 到 num),更新 dp 数组的值。
- 更新规则为:dp[i] = dp[i] or dp[i - num]。这意味着如果存在一个子集和为 i - num,那么加上 num 后,和为 i 的子集也存在。
具体步骤:
- 计算总和:total = sum(nums),如果 total 是奇数,返回 False。
- 计算目标子集和:half = total // 2。
- 初始化 dp 数组:dp = [False for _ in range(half + 1)],并设 dp[0] = True。
- 遍历 nums 更新 dp 数组:
- 对每个 j(来自 nums),从 half 到 j 更新 dp。
- 如果 j <= i,则 dp[i] = dp[i] or dp[i - j]。
- 返回 dp[half],表示是否存在一个子集其和为 half。
2.1.2 伪代码 + 逐步输出示例
# 伪代码示例
函数 canPartition(nums):total = nums 的和如果 total 是奇数:返回 Falsehalf = total // 2dp = 长度为 half + 1 的布尔数组,所有元素初始化为 Falsedp[0] = True对于 nums 中的每一个 num:从 half 到 num 遍历 i:如果 dp[i - num] 为 True:dp[i] = True返回 dp[half]# 逐步输出示例:
输入:[1, 2, 1]
初始化
• total = 1 + 2 + 1 = 4
• half = 4 // 2 = 2
• dp = [True, False, False](长度为 half + 1)
处理第一个元素 1
• 遍历 i 从 2 到 1(倒序)o i = 2: dp[2] = dp[2] or dp[1] -> False or False = Falseo i = 1: dp[1] = dp[1] or dp[0] -> False or True = True
• 更新后的 dp: [True, True, False]
处理第二个元素 2
• 遍历 i 从 2 到 2(倒序)o i = 2: dp[2] = dp[2] or dp[0] -> False or True = True
• 更新后的 dp: [True, True, True]
处理第三个元素 1
• 遍历 i 从 2 到 1(倒序)o i = 2: dp[2] = dp[2] or dp[1] -> True or True = Trueo i = 1: dp[1] = dp[1] or dp[0] -> True or True = True
• 更新后的 dp: [True, True, True]
最终结果
• 返回 dp[half]相关文章:

LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划
LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划 文章目录 LeetCode刷题 | Day 4 分割等和子集(Partition Equal Subset Sum)自底向上动态规划前言一、题目概述二、解题方法2.1 一维表格的自底向上动态规划2.1.1 思路讲解2.1.2 伪代码 + 逐…...
基于工业互联网打造敏捷供应链的实现方式:创新路径与实践应用
引言 工业互联网和敏捷供应链是当今制造业发展中的两个重要概念。工业互联网以数字化、网络化和智能化为核心,致力于将传统工业生产与互联网技术相融合,从而实现生产过程的高效、智能和灵活。而敏捷供应链则强调快速响应市场需求、灵活调整生产和供应计划…...

碳化硅柱式膜的广泛应用
碳化硅柱式膜是一种高性能的过滤材料,以其独特的性质和广泛的应用领域在现代工业中占据着重要地位。以下是对碳化硅柱式膜的详细介绍: 一、基本概述 碳化硅柱式膜是以碳化硅超滤膜为过滤单元构成的,其过滤精度高达0.1微米。这种膜材料具有耐化…...

【QT】QFont字体设置
设置字体大小 f.setPointSize(12); // 设置字体大小为12点设置字体加粗 f.setBold(true); // 使字体加粗设置字体斜体 f.setItalic(true); // 使字体斜体设置字体下划线 f.setUnderline(true); // 给字体添加下划线设置字体删除线 f.setStrikeOut(true); // 给字体添加删除…...
Vue3+vite部署nginx的二级目录,使用hash模式
修改router访问路径 import { createRouter, createWebHashHistory } from vue-routerconst router createRouter({history: createWebHashHistory (/mall4pc-bbc/),routes: [XXX,] })配置package.json文件 "build:testTwo": "vite build --mode testing --ba…...
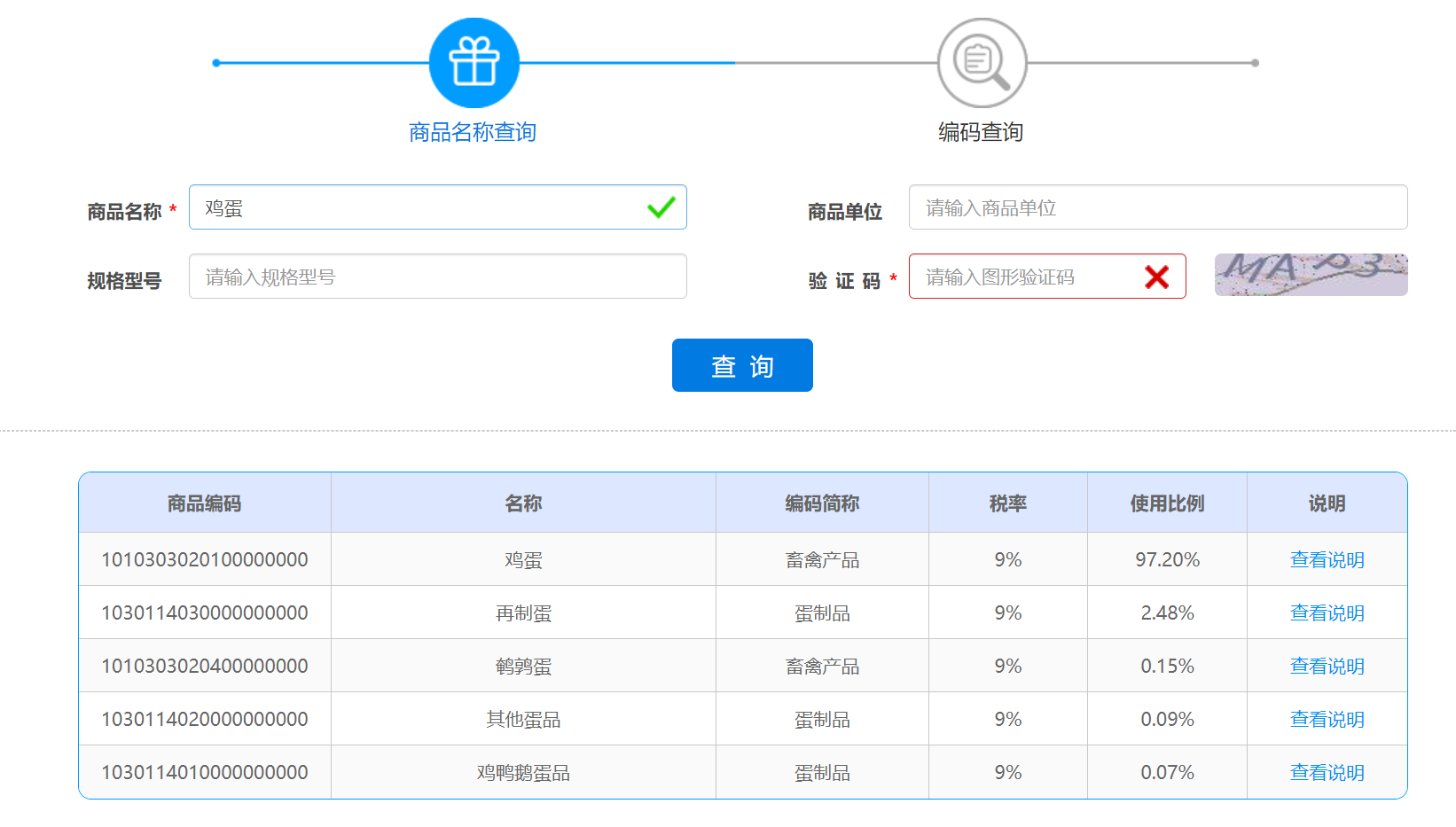
云南区块链商户平台发票助手成品
目录 1 概述2 功能对比3 项目演示图4 核心逻辑4.1智能赋码4.2 解密方法4.3 登录与检测4.4 发票金额大写转换4.5 检查登录是否失效4.6 验证码识别5 演示效果6 项目部署6.1 Web站点部署6.1.1 环境6.1.2 前端6.1.3 后端6.2 Docker部署6.2.1 构建镜像6.2.2 创建容器6.3.3 访问项目域…...

AI图书推荐:检索增强生成RAG赋能大语言模型
本书《检索增强生成RAG赋能大型语言模型》(Retrieval-Augmented Generation - Dr. Ray Islam :Mohammad Rubyet )深入探讨了如何通过结合检索系统与神经语言模型,提升人工智能在自然语言处理领域的能力。 以下是各章节内容的概要&…...
高效学习LabVIEW的方法
学习LabVIEW可以通过系统化课程、在线资源、自学实验、参与论坛、结合实际项目等多角度进行。系统课程提供全面基础,在线资源便于查漏补缺,自学实验强化理解,论坛互动解决疑难,结合实际项目应用提高实践技能。结合项目学习是最高效…...

C语言 | Leetcode C语言题解之第136题只出现一次的数字
题目: 题解: class Solution { public:vector<int> singleNumbers(vector<int>& nums) {int eor 0;for (int num:nums)eor ^ num;int rightOne eor & (~eor 1); // 提取出最右的1int onlyOne 0;for (int cur : nums) {if ((cur…...

如何利用Varjo混合现实技术改变飞机维修训练方式
自2017年以来,总部位于休斯顿的HTX实验室一直在推进混合现实技术,与美国空军密切合作,通过其EMPACT平台提供可扩展的沉浸式飞机维护虚拟现实培训。 虚拟和混合现实对维修训练的好处: l 实践技能:提供一个非常接近真实场…...

C++:按指定字符分割字符串
按指定字符分割字符串 [C]对string按指定分隔符分割(split) #include <iostream> #include <vector> #include <string> #include <sstream> using namespace std; int main() {string origin_str "hello world !"; // 需要进行分割的字符串…...

网络网络层之(6)ICMPv4协议
网络网络层之(6)ICMPv4协议 Author: Once Day Date: 2024年6月2日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: 通信网络技术_Once-Day的博客-CS…...

Opengrok代码在线查看平台
OpenGrok 是一个基于 Web 的源代码搜索引擎和交叉引用工具,它可以用来浏览和搜索代码库。虽然 OpenGrok 提供了代码搜索、查看文件和历史等功能,但它本身不是一个完整的在线集成开发环境(IDE)。然而,OpenGrok 可以作为…...

济南适宜地提取
题目: 网上下载中国的DEM、土地利用地图(1980、2000、2015年的)和一张最新济南市行政区划 图(要求:莱芜市并入济南后的区划图); 2.网上下载中国2015年年平均降水空间插值数据;3..网上下载中国2015年年平均气温空间插值数据; (注:以上数据可到资源环境科学与数据中心下载http…...

Windows 安装虚拟机(VMware+Ubuntu18.04)
Windows下虚拟机安装 一、资源下载1.1 VMware安装包下载1.2 Ubuntu镜像下载二、电脑分区三、Vmware安装四、Vmware检查4.1 注册信息查看4.2 检查网络适配器五、Ubuntu安装5.1 创建新的虚拟机5.2 打开虚拟机这是一篇介绍在Windows系统上安装Ubuntu虚拟机的操作教程。 一、资源下…...
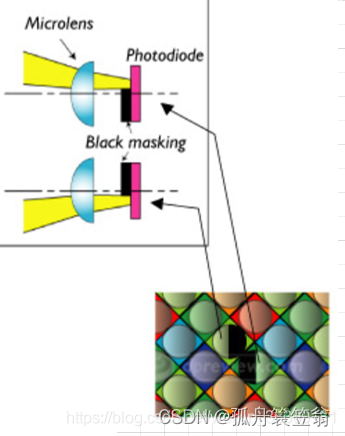
图像算法---自动对焦AF
一,CDAF反差对焦原理 CDAF,全称Contrast Detection Auto Focus,即反差式对焦或对比度检测自动对焦,是一种广泛应用于入门级数码相机和相机模块化智能手机上的自动对焦技术。以下是关于CDAF反差对焦的详细介绍: 工作原…...
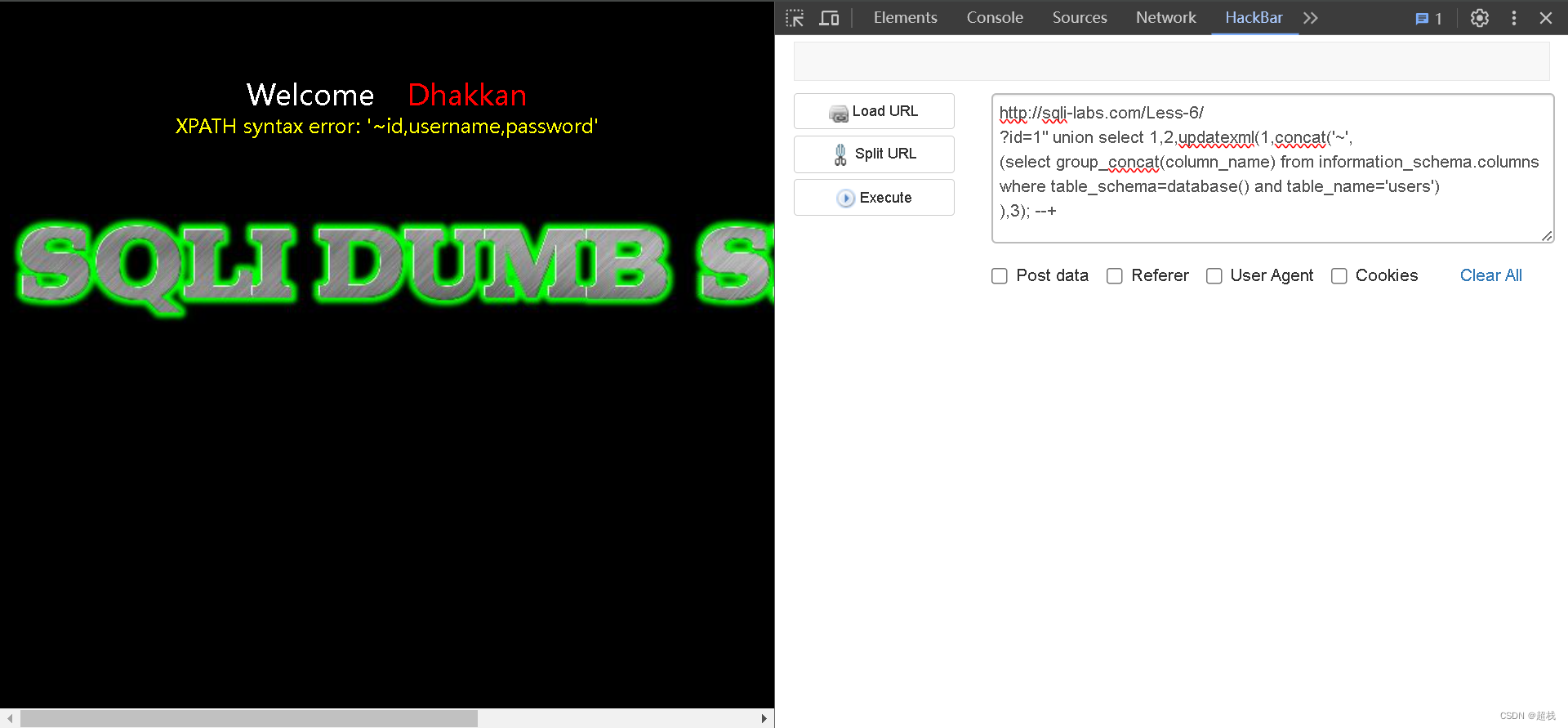
sqli-labs 靶场 less-5、6 第五关和第六关:判断注入点、使用错误函数注入爆库名、updatexml()函数
SQLi-Labs是一个用于学习和练习SQL注入漏洞的开源应用程序。通过它,我们可以学习如何识别和利用不同类型的SQL注入漏洞,并了解如何修复和防范这些漏洞。Less 5 SQLI DUMB SERIES-5 判断注入点:1. 首先,尝试正常的回显内容&#x…...

WebSocket详解与封装工具类
一、前言 在我们了解websocket之前,不妨先想想这几个问题: websocket是什么?websocket有什么好处和特点?为什么要用到websocket?什么情况下会用到websocket? 好了,带着这几个疑问一起来了解一…...

Linux学习, 进程和线程
进程 正在运行中的程序就是一个进程,进程有自己独有的内存空间和文件等等资源,进程中的资源一般都是相互隔离的。 进程内部还可以包含有多个线程,线程基本没有自己独占的资源(独有栈除外),他与进程内的其…...

SVM模型实现城镇居民月平均消费数据分类
SVM模型实现城镇居民月平均消费数据分类 一、SVM支持向量机简介二、数据集介绍三、SVM建模流程及分析一、SVM支持向量机简介 支持向量机是由感知机发展而来的机器学习算法,属于监督学习算法。支持向量机具有完备的理论基础,算法通过对样本进行求解,得到最大边距的超平面,并…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
