TSP(Python):Qlearning求解旅行商问题TSP(提供Python代码)
一、Qlearning简介
Q-learning是一种强化学习算法,用于解决基于奖励的决策问题。它是一种无模型的学习方法,通过与环境的交互来学习最优策略。Q-learning的核心思想是通过学习一个Q值函数来指导决策,该函数表示在给定状态下采取某个动作所获得的累积奖励。
Q-learning的训练过程如下:
1. 初始化Q值函数,将所有状态-动作对的Q值初始化为0。
2. 在每个时间步,根据当前状态选择一个动作。可以使用ε-greedy策略来平衡探索和利用。
3. 执行选择的动作,并观察环境返回的奖励和下一个状态。
4. 根据Q值函数的更新规则更新Q值。Q值的更新公式为:Q(s, a) = Q(s, a) + α * (r + γ * max(Q(s', a')) - Q(s, a)),其中α是学习率,γ是折扣因子,r是奖励,s是当前状态,a是选择的动作,s'是下一个状态,a'是在下一个状态下选择的动作。
5. 重复步骤2-4,直到达到停止条件。
Q-learning的优点是可以在没有先验知识的情况下自动学习最优策略,并且可以处理连续状态和动作空间。它在许多领域中都有广泛的应用,如机器人控制、游戏策略和交通路线规划等。
二、TSP问题介绍
旅行商问题(Traveling salesman problem, TSP)是一个经典的组合优化问题,它可以描述为一个商品推销员去若干城市推销商品,要求遍历所有城市后回到出发地,目的是选择一个最短的路线。当城市数目较少时,可以使用穷举法求解。而随着城市数增多,求解空间比较复杂,无法使用穷举法求解,因此需要使用优化算法来解决TSP问题。TSP问题的应用非常广泛,不仅仅适用于旅行商问题本身,还可以用来解决其他许多的NP完全问题,如邮路问题、转配线上的螺母问题和产品的生产安排问题等等。因此,对TSP问题的有效求解具有重要意义。解决TSP问题的方法有很多,其中一种常用的方法是蚁群算法。除了蚁群算法,还有其他一些常用的解决TSP问题的方法,如遗传算法、动态规划和强化学习等。这些方法各有特点,适用于不同规模和特征的TSP问题。
三、Qlearning求解TSP问题
1、部分代码
可以自动生成地图也可导入自定义地图,只需要修改如下代码中chos的值即可。
import matplotlib.pyplot as plt
from Qlearning import Qlearning
#Chos: 1 随机初始化地图; 0 导入固定地图
chos=0
node_num=41 #当选择随机初始化地图时,自动随机生成node_num-1个城市
# 创建对象,初始化节点坐标,计算每两点距离
qlearn = Qlearning(alpha=0.5, gamma=0.01, epsilon=0.5, final_epsilon=0.05,chos=chos,node_num=node_num)
# 训练Q表、打印路线
iter_num=1000#训练次数
Curve,BestRoute,Qtable,Map=qlearn.Train_Qtable(iter_num=iter_num)
#Curve 训练曲线
#BestRoute 最优路径
#Qtable Qlearning求解得到的在最优路径下的Q表
#Map TSP的城市节点坐标## 画图
plt.figure()
plt.ylabel("distance")
plt.xlabel("iter")
plt.plot(Curve, color='red')
plt.title("Q-Learning")
plt.savefig('curve.png')
plt.show()
2、部分结果
(1)以国际通用的TSP实例库TSPLIB中的测试集bayg29为例:
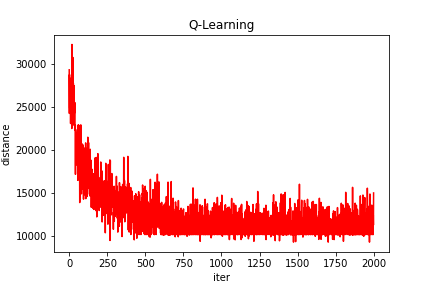
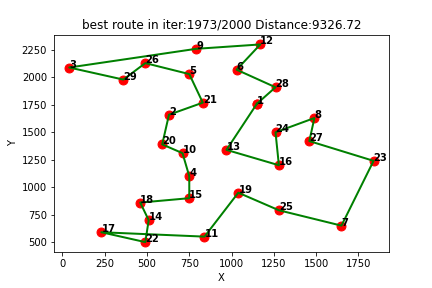
Q-learning得到的最短路线: [1, 28, 6, 12, 9, 3, 29, 26, 5, 21, 2, 20, 10, 4, 15, 18, 14, 22, 17, 11, 19, 25, 7, 23, 27, 8, 24, 16, 13, 1]
(2)随机生成25个城市


Q-learning得到的最短路线: [1, 16, 11, 20, 25, 3, 5, 12, 4, 17, 21, 13, 22, 18, 15, 23, 24, 7, 8, 2, 14, 9, 6, 10, 19, 1]
(3)随机生成35个城市
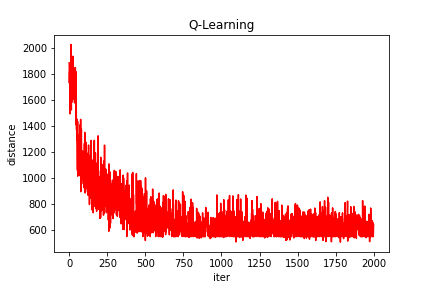
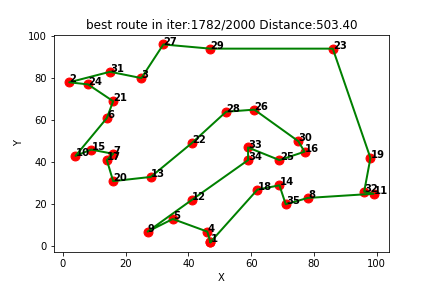
Q-learning得到的最短路线: [1, 4, 5, 9, 12, 34, 33, 25, 16, 30, 26, 28, 22, 13, 20, 17, 7, 15, 10, 6, 21, 24, 2, 31, 3, 27, 29, 23, 19, 32, 11, 8, 35, 14, 18, 1]
四、完整Python代码
TSP(Python):Qlearning求解旅行商问题TSP(提供Python代码)
文件夹内包含完整Python代码,点击main.py即可运行,可以自定义TSP数据集。
点击main.py即可运行
在main.py中,修改如下值chos
当chos=0时,导入data.txt的城市坐标数据
当chos=1时,随机生成node_num-1个城市坐标
iter_num是最大训练次数
Curve 是训练曲线
BestRoute 是最优路径
Qtable Qlearning是求解得到的在最优路径下的Q表
Map是 TSP的城市节点坐标
相关文章:

TSP(Python):Qlearning求解旅行商问题TSP(提供Python代码)
一、Qlearning简介 Q-learning是一种强化学习算法,用于解决基于奖励的决策问题。它是一种无模型的学习方法,通过与环境的交互来学习最优策略。Q-learning的核心思想是通过学习一个Q值函数来指导决策,该函数表示在给定状态下采取某个动作所获…...
【精通NIO】NIO介绍
一、什么是NIO NIO,全称为New Input/Output,是Java平台中用于替代传统I/O(Blocking I/O)模型的一个功能强大的I/O API。NIO在Java 1.4版本中被引入,其设计目标是提供一种非阻塞的、低延迟的I/O操作方式,以…...

ssh远程管理
一、Openssh概述 Openssh是一种安全通道协议,用来实现字符界面的远程登录、远程复制、远程文本传输。 Openssh对通信双方的数据进行了加密。有两种方式: 用户名和密码登录:比较常用密钥对认证方式:可以实现免密登录 ssh端口&a…...
【ai】pycharm远程ssh开发
方式1: gateway的方式是远程放一个pycharm 专业版,经常下载失败 方式2: 类似vs,源码本地,同步到远程进行运行。 参考大神的分享: Pycharm远程连接服务器(2023-11-9) Pycharm远程连接服务器(windows下远程修改服务器代码)[通俗易懂] cpolar 建议同时内网穿透 选 远程开…...

leetcode 9 回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如,121 是回文,而…...

学习Python的基础知识
目录 摘要 Python 的主要特点 基本语法 1. 变量和数据类型: 2. 条件语句: 3. 循环: 4. 函数: 5. 类和对象: 6. 列表和字典: 7. 文件I/O: Python 的学习路线 如何高效使用 Python 的…...
)
第五届上海市青少年算法竞赛网络同步赛(小学组)
第五届上海市青少年算法竞赛网络同步赛(小学组)T1. 符号译码_网络同步赛 内存限制: 256 Mb 时间限制: 1000 ms 题目描述 小爱为标点符号设计了一套编码系统,编码规则如下: [ 的编码为 010 ] 的编码为 101 < 的编码为 00 > 编码为 11 + 的编码为 011 - 编码为 100 根…...

【区分vue2和vue3下的element UI Cascader 级联选择器组件,分别详细介绍属性,事件,方法如何使用,并举例】
在Vue 2的Element UI和Vue 3的Element Plus中,el-cascader(级联选择器)组件用于从嵌套的数据中进行选择。以下是对这两个版本下el-cascader组件的属性、事件和方法的详细介绍,并附带示例。 Vue 2的Element UI el-cascader 属性…...
pottery,一个超酷的 Python 库!
更多Python学习内容:ipengtao.com 大家好,今天为大家分享一个超酷的 Python 库 - pottery。 Github地址:https://github.com/brainix/pottery 在分布式系统和高并发环境中,Redis 作为一种高性能的键值存储数据库,被广泛…...

【Android面试八股文】在Java中重载和重写是什么意思,区别是什么?
文章目录 在Java中重载和重写是什么意思,区别是什么?这道题想考察什么 ?考察的知识点考生应该如何回答重载(Overloading)重写(Overriding)重载和重写的区别在Java中重载和重写是什么意思,区别是什么? 这道题想考察什么 ? Java基础 考察的知识点 面向对象多态的基…...

【第二篇】SpringSecurity源码详解
一、SpringSecurity中的核心组件 在SpringSecurity中的jar分为4个,作用分别为 jar作用spring-security-coreSpringSecurity的核心jar包,认证和授权的核心代码都在这里面spring-security-config如果使用Spring Security XML名称空间进行配置或Spring Security的Java configura…...

基于Python+FFMPEG环境下载B站歌曲
题主环境 WSL on Windows10 命令如下 # python3.9 pip install --pre yutto yutto --batch https://www.bilibili.com/video/BV168411o7Bh --audio-only ls | grep aac | xargs -I {} ffmpeg -i {} -acodec libmp3lame {}.mp3WinAmp...
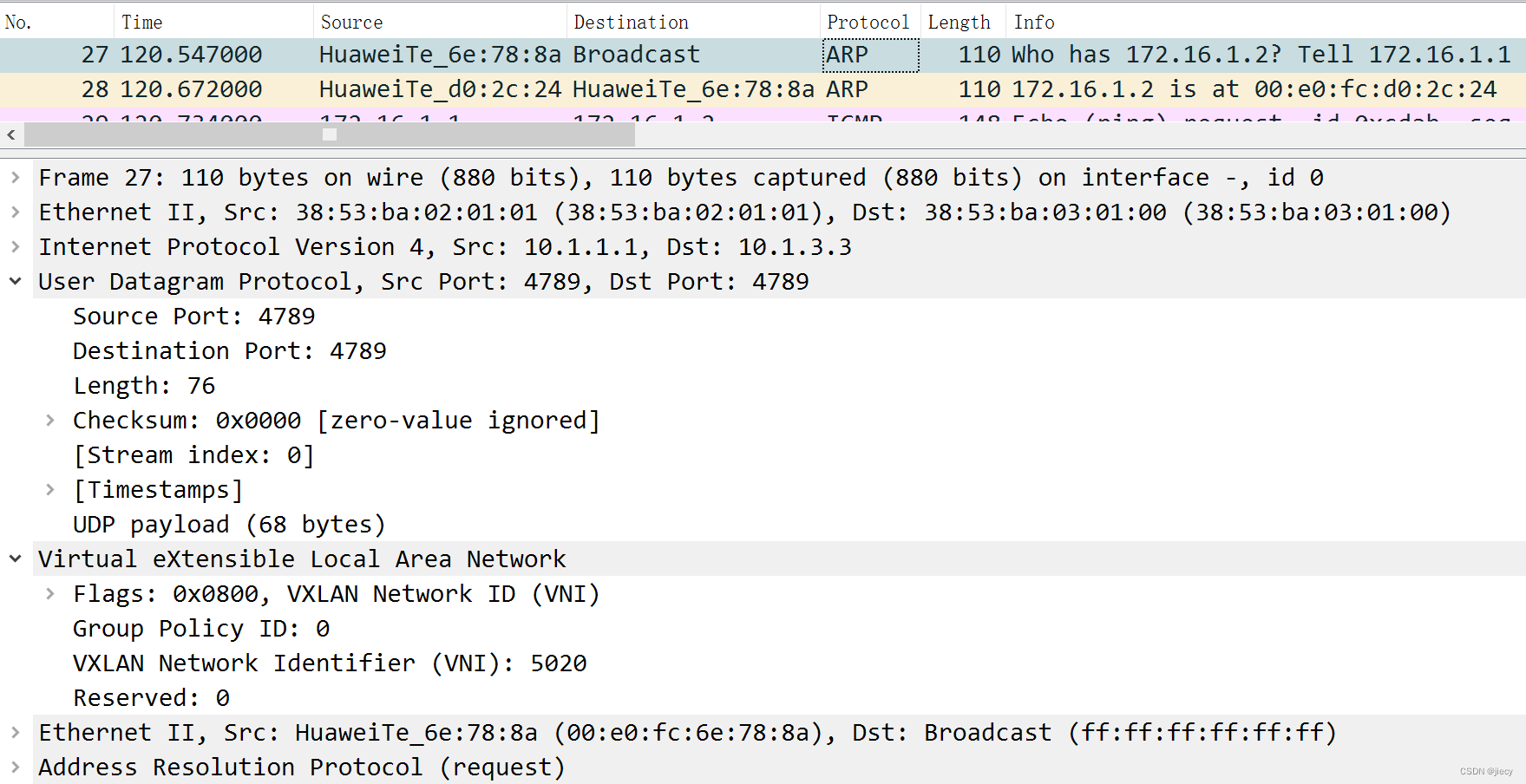
静态 VxLAN 浅析及配置示例(头端复制)
一、概念: VxLAN:Visual eXtensible Local Area Network 虚拟扩展本地局域网,一种隧道技术,能在三层网络的基础上建立二层以太网网络隧道,从而实现跨地域的二层互连,VxLAN端口:4789EVPN&#x…...

2023年与2024年AI代理基础设施的演进:六大关键变化
随着人工智能技术的不断进步,AI代理基础设施在2023年和2024年之间经历了显著的发展和变革。本文将探讨这两年间AI代理基础设施的六大关键变化,展示如何为开发者和用户提供更加强大和集成化的解决方案。 1. 代理特定开发工具的兴起 2024年见证了专为AI代理设计的新一代开发工…...

实验三-8086指令的应用《计算机组成原理》
一、实验目的 掌握8086指令的应用 二、实验原理 三、实验仪器 计算机1台,emu8086软件。 四、实验步骤 1、建立00H~0FH~00H 31个数,00H~0FH数据逐渐增大,0FH~00H逐渐减小,即DI指针所表示的地…...
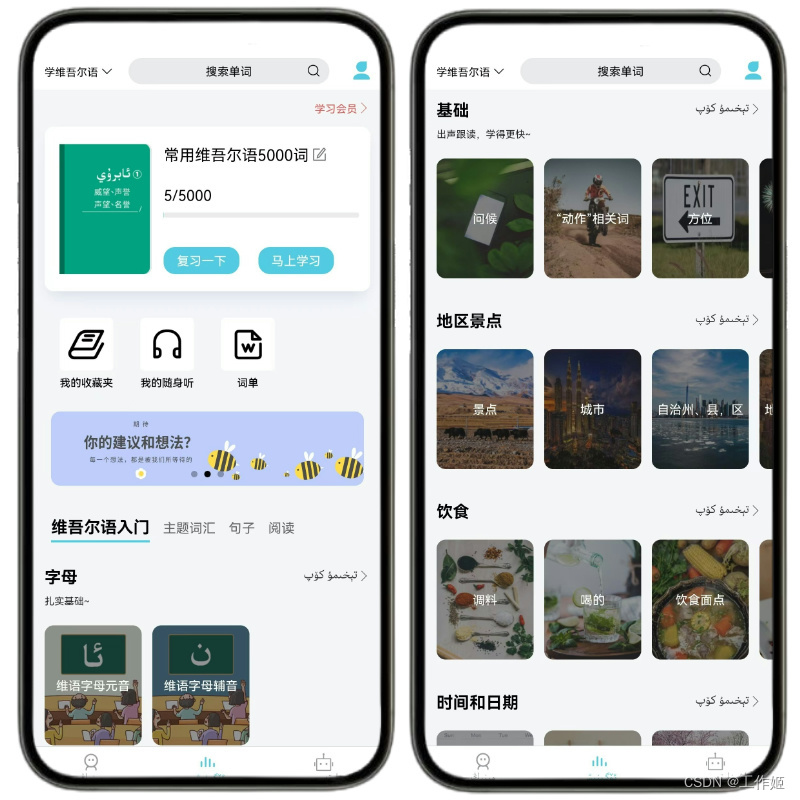
《维汉翻译通》App全新升级:维吾尔语短文本翻译、汉语拼音标注、维语词典、谚语格言名句等功能统统免费!还支持维吾尔文OCR识别提取文字!
2024年《维汉翻译通》App迎来重大更新!这次升级不仅带来了全新的功能,还为所有用户提供了更加便捷的服务体验。以下是我们新版本的主要亮点: 维语短文本翻译免费啦! 我们深知语言是沟通的桥梁,为了让更多人能够跨越语…...

全年申报!2024年陕西省双软企业认定条件标准、申报好处费用
1.双软企业是什么? 答:双软认证并不是一个资质,而是"软件产品登记"和"软件企业认定"两个不同资质的统称.叫做"双软企业" 2.双软企业的优惠政策是什么? 答:(1)软件产品登记的优惠政策:软件产品增值税,从13%减按3%征收,实行即征即退; (2)软件…...
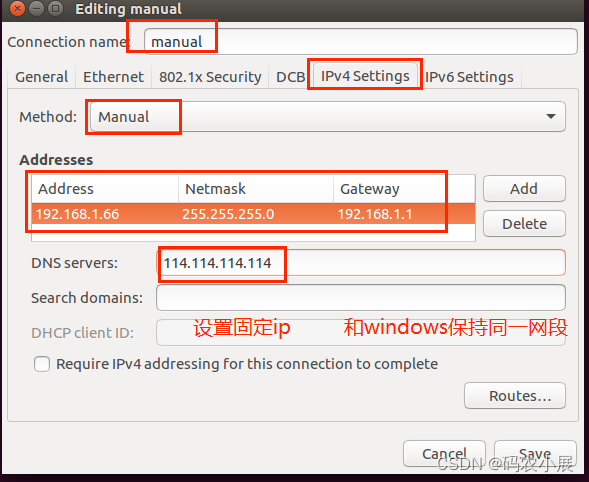
系统移植 (以将Linux系统移植到S5P6818开发板为例)
(本篇文章以将Linux系统移植到S5P6818开发板为例) 本文章所需要的文件在下面链接获取:https://download.csdn.net/download/a1547998353/89406544 开发环境搭建 1、安装交叉编译工具链 安装步骤: 1. 在ubuntu的家目录(~)下,创建t…...

超长正整数的加法
一、引言 在计算机科学中,整数加法是一个基础且重要的操作。然而,当面对超长正整数(即超出计算机内置整数类型表示范围的整数)时,传统的整数加法方法便不再适用。超长正整数通常使用字符串或数组来表示,每…...
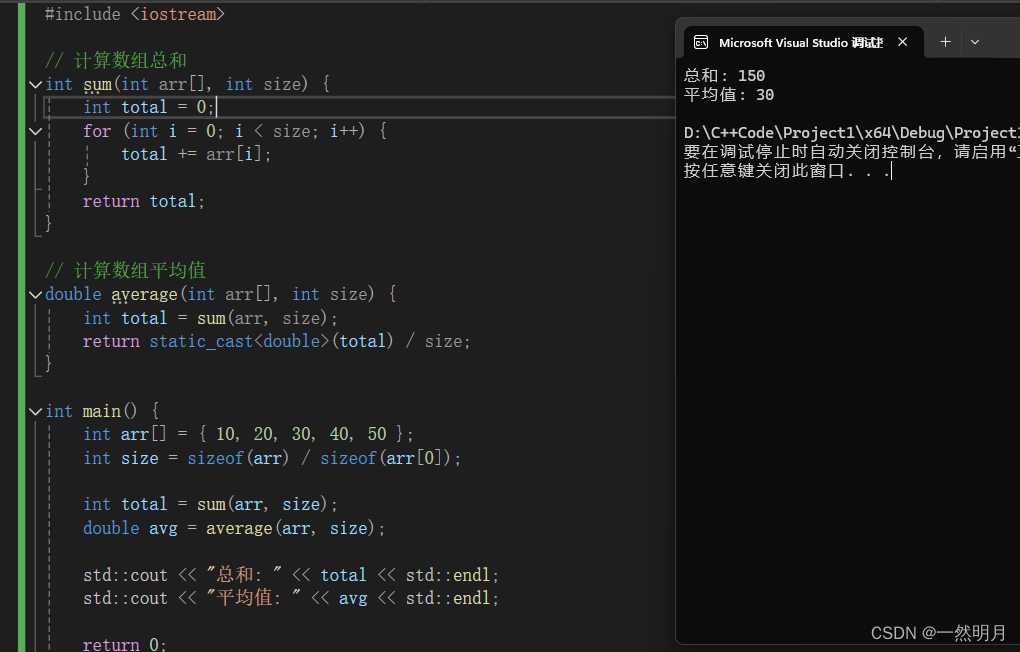
C++ - 查找算法 和 其他 算法
目录 一. 查找算法: 1.顺序查找: 2.二分查找: 二. 其他算法: 1.遍历算法: 2.求和、求平均值等聚合算法。 a.求和算法: b.求平均值算法: 一. 查找算法: 1.顺序查找࿱…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
