【因果推断python】24_倾向得分2

目录

倾向加权

倾向得分估计

---

倾向加权

好的，我们得到了倾向得分。怎么办？就像我说过的，我们需要做的就是以此为条件。例如，我们可以运行一个线性回归，它仅以倾向得分为条件，而不是所有的 X。现在，让我们看一下只使用倾向得分而不使用其他任何东西的技术。这个想法是用倾向得分写出均值的条件差

我们可以进一步简化这一点，但让我们这样看一下，因为它让我们对倾向得分的作用有了一些很好的直觉。第一项是估计 Y1。它应用于所有接受干预的对象，并按接受干预的逆概率对它们的权重进行缩放。这样做的目的是使那些接受干预的可能性非常低的人权重增加。想想看，这是有道理的，对吧？如果某人接受干预的可能性很低，那么该人看起来就像未经干预的人。然而，同一个人受到了干预。这一定很有趣。我们有一个看起来像未经干预的被干预对象，因此我们将给予该实体较高的权重。这样做的目的是创建一个与原始全样本相同大小的群体，但每个人都受到干预。出于同样的原因，另一个术语着眼于未经干预的人，并赋予那些看起来像经过干预的人很高的权重。这个估计器被称为干预加权的逆概率（IPTW），因为它通过接受除它所接受的干预之外的某种其他影响的概率来缩放每个单元的权重。

在下面在图片中，就展示了这种加权的作用。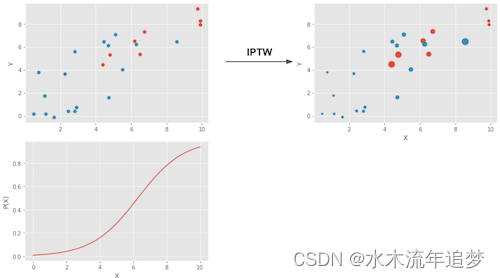

左上图显示了原始数据。蓝点是未干预的，红点是干预过的。底部图显示了倾向得分 P(x)。注意它是如何在 0 和 1 之间的，并且随着 X 的增加而增长。最后，右上图是加权后的数据。注意更靠左的红色（处理过的）（倾向得分较低）的权重更高。同样，右侧的蓝色图也具有更高的权重。现在我们有了直觉，我们可以将上面的术语简化为如果我们对 X 进行积分，它就会成为我们的倾向得分加权估计量。

请注意，此估计器要求 P(x) 和 1−P(x)  大于零。换句话说，这意味着每个人都需要至少有一些机会接受干预和不接受干预。说明这一点的另一种方式是干预和未干预样本的分布需要重叠。这是因果推理的正值假设（positivity assumption）。它也具有直觉意义。如果干预和未干预的样本不重叠，这意味着它们非常不同，我将无法将一组的效果外推到另一组。这种推断并非不可能（回归做到了），但它非常危险。这就像在实验中测试一种新药，只有男性接受治疗，然后假设女性对它的反应同样好。

倾向得分估计

在一个理想的世界中，我们会有真实的倾向得分P(X)。 然而，在实践中，分配干预的机制是未知的，我们需要用对它的估计来替换真实的倾向得分 。 这样做的一种常见方法是使用逻辑回归，但也可以使用其他机器学习方法，如梯度提升（尽管它需要一些额外的步骤来避免过度拟合）。

在这里，我将坚持逻辑回归。 这意味着我必须将数据集中的分类特征转换为假人。

categ = ["ethnicity", "gender", "school_urbanicity"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]data_with_categ = pd.concat([data.drop(columns=categ), # dataset without the categorical featurespd.get_dummies(data[categ], columns=categ, drop_first=False)# categorical features converted to dummies
], axis=1)print(data_with_categ.shape)(10391, 32)

现在让我们使用逻辑回归（logistic regression）来估计倾向得分。

from sklearn.linear_model import LogisticRegressionT = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])ps_model = LogisticRegression(C=1e6).fit(data_with_categ[X], data_with_categ[T])data_ps = data.assign(propensity_score=ps_model.predict_proba(data_with_categ[X])[:, 1])data_ps[["intervention", "achievement_score", "propensity_score"]].head()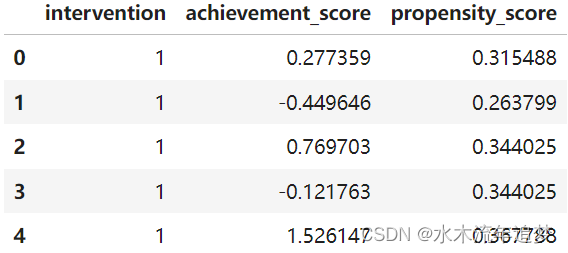

首先，我们可以确保倾向得分权重确实重建了每个人都得到干预的人群。 通过产生权重1/P(X)，它创建了每个人都被对待的群体，并通过提供权重1/(1−P(X))，它创建了群体，其中 每个人都没有得到干预。

weight_t = 1/data_ps.query("intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("intervention==0")["propensity_score"])
print("Original Sample Size", data.shape[0])
print("Treated Population Sample Size", sum(weight_t))
print("Untreated Population Sample Size", sum(weight_nt))

Original Sample Size 10391
Treated Population Sample Size 10388.604824722199
Untreated Population Sample Size 10391.4305248224

我们还可以使用倾向得分来找到混淆的证据。 如果人群中的一个细分群体的倾向得分高于另一个群体，这意味着不是随机的东西导致了干预。 如果同样的事情也导致了结果，我们就会感到困惑。 在我们的案例中，我们可以看到自称更有野心的学生也更有可能参加成长心态研讨会。

sns.boxplot(x="success_expect", y="propensity_score", data=data_ps)
plt.title("Confounding Evidence");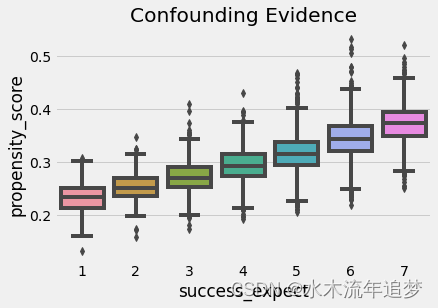

我们还必须检查干预和未干预人群之间是否存在重叠。 为此，我们可以看到倾向得分在未干预者和被干预者上的经验分布。 查看下图，我们可以看到没有人的倾向得分为零，即使在倾向得分较低的区域，我们也可以找到接受干预和未接受干预的个体。 这就是我们所说的经过良好平衡的干预和未干预人群。

sns.distplot(data_ps.query("intervention==0")["propensity_score"], kde=False, label="Non Treated")
sns.distplot(data_ps.query("intervention==1")["propensity_score"], kde=False, label="Treated")
plt.title("Positivity Check")
plt.legend();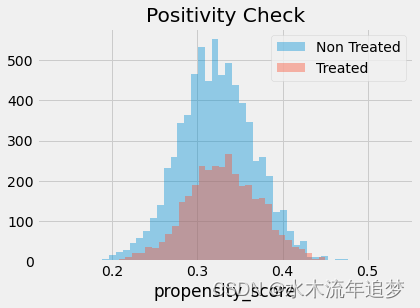

最后，我们可以使用倾向得分加权估计器来估计平均干预效果（ATE）。

weight = ((data_ps["intervention"]-data_ps["propensity_score"]) /(data_ps["propensity_score"]*(1-data_ps["propensity_score"])))y1 = sum(data_ps.query("intervention==1")["achievement_score"]*weight_t) / len(data)
y0 = sum(data_ps.query("intervention==0")["achievement_score"]*weight_nt) / len(data)ate = np.mean(weight * data_ps["achievement_score"])print("Y1:", y1)
print("Y0:", y0)
print("ATE", np.mean(weight * data_ps["achievement_score"]))

Y1: 0.2595774244866067
Y0: -0.12892090981713242
ATE 0.38849833430373715

倾向得分加权表示，就成就而言，我们应该期望接受干预的个体比未经干预的同伴高 0.38 个标准差。 我们还可以看到，如果没有人得到干预，我们应该期望成绩的总体水平比现在低 0.12 个标准差。 同样的道理，如果我们为每个人提供研讨会，我们应该期望一般成就水平高出 0.25 个标准差。 将此与我们通过简单比较干预和未干预得到的 0.47 ATE 估计值进行对比。 这证明我们的偏差确实是正向的，并且控制 X 让我们对成长心态的影响有了更适度的估计。