数据结构-AVL树
目录
二叉树
二叉搜索树的查找方式:
AVL树
AVL树节点的实现
AVL树节点的插入操作
AVL树的旋转操作
右旋转:
左旋转:
左右双旋:
右左双旋:
AVL树的不足和下期预告(红黑树)
二叉树
了解AVL树之前,需要先了解一下二叉搜索树的概念,二叉搜索树具有以下性质:
1,如果左子树不为空,则左子树上所有节点的值都小于跟节点的值。
2,如果右子树不为空,则右子树的所有节点的值都大于跟节点的值。
3,根节点的左右子树也是一颗二叉搜索树。
如果使用二叉树的中序遍历方法来遍历一颗二叉树,则可以得到一个有序的序列。
二叉搜索树的查找方式:

根据上图可以对二叉树进行查找从而得到我们想要的节点。
一个完全二叉树的查找效率可以达到 级别,但如果我们插入的数值都是大于根节点的数值,并且是严格递增的,那么此时整个二叉树就会退化成一个链表的结构,那么此时查找的效率也会退化成
。因此我们就需要考虑一个问题,无论何时进行插入,都可以让二叉树,保持左右子树的相对平衡,随时更改根节点,这样就可以让查找的时间复杂度一直保持在
,所以研究者引入了AVL树的概念。
AVL树
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
AVL树它本质上其实还是一个二叉树,它的特点符合二叉树的所有特点,在此之外,AVL树还具有平衡的性质,也就是说,它的左子树和右子树的高度差的绝对值不会大于1,因此这样也就保证了AVL树的查找效率。
AVL树节点的实现
为了实现AVL树,我们需要先定义树的节点,和普通的二叉树不同,在定义节点的时候,我们也需要在其中定义一个平衡因子,我们使用bf(balance factor)来表示:AVL树的节点定义如下:
class TreeNode{//定义树的左右节点索引和父亲索引public TreeNode left = null;public TreeNode right = null;public TreeNode parent = null;public int val;public int bf;//定义构造函数public TreeNode (int val){this.val = val;}
}我们定义当前节点的平衡因子 = 右树的高度 - 左树的高度。如果当前节点的bf<0,那么左树就高,bf>0右树就高。bf = 0,那么两边一样高。当然这只是其中的一种实现方式而已(本文是这么定义的)。
AVL树节点的插入操作
首先,我们将其分为两步
1,按照二叉树的插入方式进行插入。
2,对不满足条件的节点进行旋转,使树达到平衡。
此时可以看下接下来这几幅图:
 |  |
 | 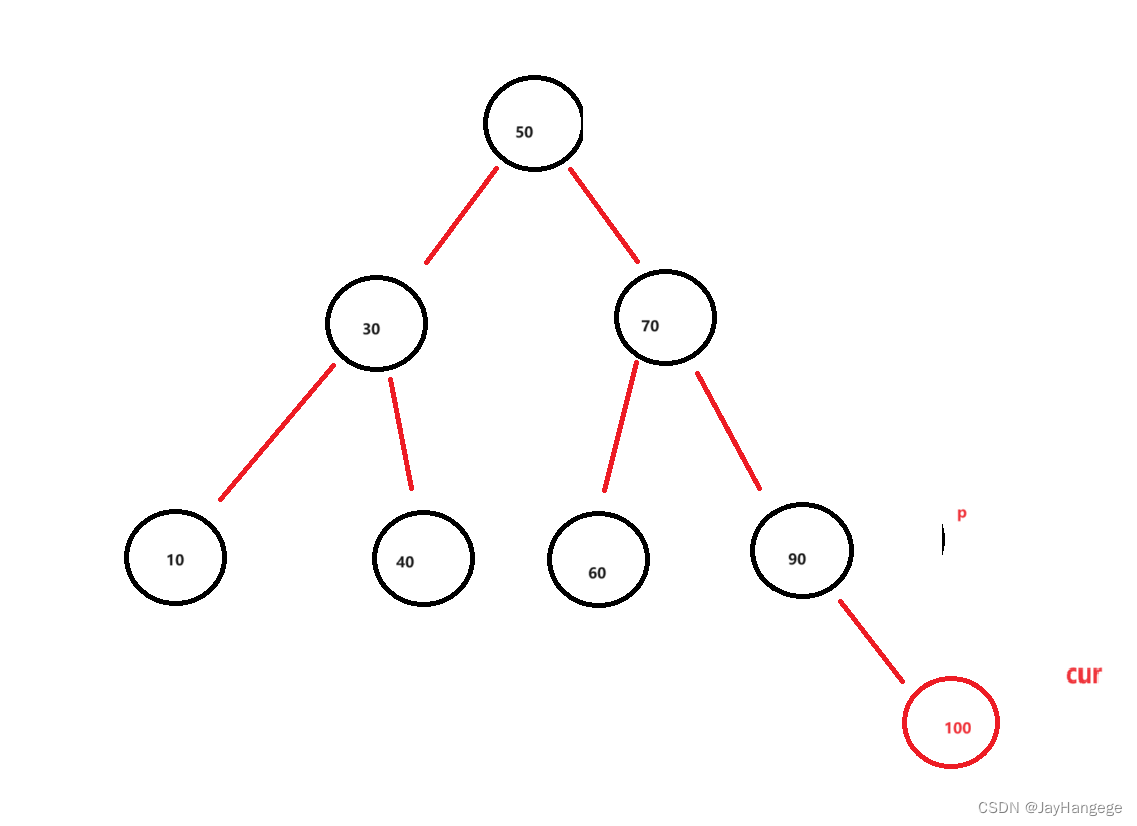 |
假设我要在二叉树种插入一个值为100,那么此时我应该找到100应该插入到哪个位置,每一次寻找定义cur为要插入的位置,定义parent为cur的父亲节点,那么遍历下来就可以找到插入的位置,此时代码如下:
public TreeNode root ;public void insert(int val){//1,首先先进行节点的插入操作;TreeNode node = new TreeNode(val);if(this.root == null){//如果树为空,那么node就是新的rootthis.root = node;}else{TreeNode parent = null;TreeNode cur = this.root;// 1.1 先判断要插入的位置,然后再进行插入while(cur != null){if(cur.val < val){parent = cur;cur = cur.right;} else if (cur.val == val) {return;}else{parent = cur;cur = cur.left;}}//此时找到了要插入的位置,对node进行插入,插入的位置为parent所指向的节点//判断往左边插入还是右边插入,然后再让node指回去。if(parent.val < val){parent.right = node;}else{parent.left = node;}node.parent = parent;cur = node;}}一定要让node指向指回去,否则子节点会丢失父节点的索引。
AVL树的旋转操作
基于以上的插入,我们可以发现一个问题,就是说,如果每次都插入比上一次大的值,那么势必会让这个树退化成一个链表,那么此时树的存储结构优势将会丢掉,所以AVL树引入了旋转操作来对树进行操作。从而使得这棵树不会退化成链表。
cur插入后,parent的平衡因子一定需要调整,
在插入之前,parent的平衡因子分为三种情况:-1,0, 1
插入时分以下两种情况:
1. 如果cur插入到parent的左侧,只需给parent的平衡因子 -1 即可
2. 如果cur插入到parent的右侧,只需给parent的平衡因子 +1 即可
此时:parent的平衡因子可能有三种情况:0,正负1, 正负2
1. 如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功
2. 如果parent的平衡因子为正负1,说明插入前parent的平衡因子为0,插入后被更新成正负1,此时以parent为根的树的高度增加,需要继续向上更新
3. 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进行旋转处理
此时更新操作就如下:
while(){//更新parent的平衡因子if(cur == parent.right){parent.bf++;}else{parent.bf--;}//更新后的平衡因子为0,说明插入后的结果是平衡的,此时无需后续操作if(parent.bf == 0){return;}if(parent.bf != 1 && parent.bf != -1){//此时需要继续向上更新if(parent.bf == 2){if(cur.bf == 1){// parent.bf == 2 cur.bf == 1}else{// parent.bf == 2 cur.bf == -1}}else{if(cur.bf == 1){// parent.bf == -2 cur.bf == 1}else{// parent.bf == -2 cur.bf == -1}}}}那么基于以上操作,我们的更新平衡因子的模板已经搭好了,但是在什么情况下需要进行旋转呢?
右旋转:
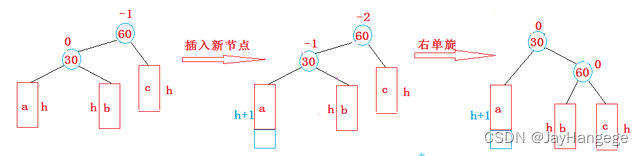
假设有上面这种情况,原来的cur.bf == 0 , 但是parent.bf == -1 ,此时在左树的最左边插入一个节点,那么此时的节点情况就变成了cur.bf == -1 , parent.bf == -2 。那么此时就需要对parent节点进行右旋转,从而调整树的结构。
此时需要注意以下几点:
1. 30 节点的右孩子可能存在,也可能不存在。
2. 60 可能是根节点,也可能是子树。如果是根节点,旋转完成后,要更新根节点 如果是子树,可能是某个节点的左子树,也可能是右子树。
 |  |  |
在上图中可以看出,当我们想进行右转操作时,需要将parent.left 标记为 subL,将subL.right标记为subLR.

从2图转换为3图可以如上图表示:
1. 修改parent.left = subLR;
2. 修改subL.right = parent;
3. 修改 subLR.parent = parent (此时需要判断subLR是否为空)
4. 保存parent的父亲节点(祖父节点)
5. 修改parent的父亲节点指向subL;
6. 修改祖父节点指向subL(需要确认祖父节点是否存在,如果不存在则parent是根节点)
7. 修改subL.parent属性为祖父节点;
8. 判断完了之后还要修改平衡因子。
代码如下:
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if(subLR != null){subLR.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subL;if(parent == this.root){this.root = subL;this.root.parent = null;}else{if(pParent.left == parent){pParent.left = subL;}else{pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}左旋转:
左旋转和右旋转的逻辑是一样的,不过是对称的操作。以下是左旋转的代码演示:
此时最初的parent的bf值为1,进行添加节点之后,则是会变成parent.bf 会变成2,此时的cur.bf
会变成1(因为给cur的右树增加了一层)。此时就需要用到左旋转的方法来进行旋转,从而降低AVL树的高度了。具体代码如下:和右旋转是对称的
private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if(subRL != null){subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if(parent == this.root){this.root = subR;this.root.parent = null;}else{if(pParent.left == parent){pParent.left = subR;}else{pParent.right =subR;}subR.parent = pParent;}subR.bf = parent.bf = 0;}左右双旋:
讲完了上述两种比较简单的情况,其实还有两种比较复杂的情况,比如说,

假如说是上面这种情况呢,此时我要插入的值为40,但是60节点bf更新为-2,此时的30这个节点的bf值为1,50节点bf值为-1,这时候单纯的旋转已经无法解决这些问题了。因此
此时先对30进行左旋转:可以得到50节点bf为-2,60节点 bf 为-2,30节点 bf 为 0
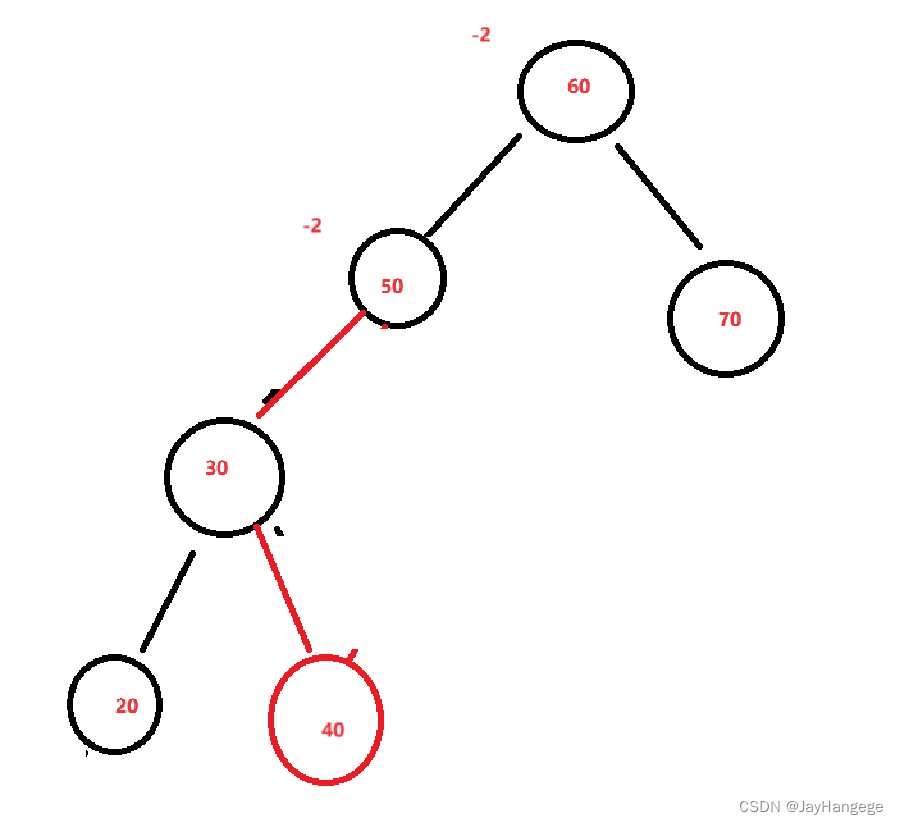
此时再对60节点进行右旋转:此时的50节点 bf 为 0 ,60节点bf为 1 此时的 AVL树已经达到了平衡。

private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;this.rotateRight(parent.left);this.rotateLeft(parent);if (bf == -1) {parent.bf = 1;subL.bf = 0;subLR.bf = 0;} else if (bf == 1) {subL.bf = -1;subLR.bf = 0;parent.bf = 0;}
}右左双旋:
和左右双旋是对称的概念,此处便不再赘述了。
直接贴代码:
private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;this.rotateRight(parent.right);this.rotateLeft(parent);if(bf == 1){parent.bf = -1;subR.bf = 0;subRL.bf = 0;} else if (bf == -1) {parent.bf = 0;subR.bf = 1;subRL.bf =0;}}总之AVL树,就是为了让整个树不退化成链表,才引入的旋转机制。
AVL树的不足和下期预告(红黑树)
但是AVL树虽然保证了查询的效率,但是还是有一些机制上的问题,比如说,旋转非常消耗时间,比如我们在单旋的时候已经进行了8步操作,这只是其中的一次插入,当数据大量插入的时候AVL树显然是不够用的,因此科学家们又引入了红黑树的机制。下一次我会继续写关于红黑树的博客,希望大家能够多多点赞。
相关文章:

数据结构-AVL树
目录 二叉树 二叉搜索树的查找方式: AVL树 AVL树节点的实现 AVL树节点的插入操作 AVL树的旋转操作 右旋转: 左旋转: 左右双旋: 右左双旋: AVL树的不足和下期预告(红黑树) 二叉树 了…...

数字科技如何助力博物馆设计,强化文物故事表现力?
国际博物馆日是每年为了推广博物馆和文化遗产,而设立的一个特殊的日子,让我们可以深入探讨博物馆如何更好地呈现和保护我们的文化遗产,随着近年来的数字科技发展,其在博物馆领域的应用越来越广泛,它为博物馆提供了新的…...

德克萨斯大学奥斯汀分校自然语言处理硕士课程汉化版(第七周) - 结构化预测
结构化预测 0. 写在大模型前面的话1. 词法分析 1.1. 分词1.2. 词性标注 2.2. 句法分析 2.3. 成分句法分析2.3. 依存句法分析 3. 序列标注 3.1. 使用分类器进行标注 4. 语义分析 0. 写在大模型前面的话 在介绍大语言模型之前,先把自然语言处理中遗漏的结构化预测补…...

5-Maven-setttings和pom.xml常用配置一览
5-Maven-setttings和pom.xml常用配置一览 setttings.xml配置 <?xml version"1.0" encoding"UTF-8"?> <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xs…...

input输入框设置样式
input清除自带样式 input, textarea,label, button,select,img,form,table,a{-webkit-tap-highlight-color: rgba(255,255,255,0);-webkit-tap-highlight-color: transparent;margin: 0;padding: 0;border: none; } /*去除iPhone中默认的input样式*/ input, button, select, t…...

平稳交付 20+ 医院,卓健科技基于 OpenCloudOS 的落地实践
导语:随着数字化转型于各个行业领域当中持续地深入推进,充当底层支撑的操作系统正发挥着愈发关键且重要的作用。卓健科技把 OpenCloudOS 当作首要的交付系统,达成了项目交付速度的提升、安全可靠性的增强、运维成本的降低。本文将会阐述卓健科…...
Python下载库
注:本文一律使用windows讲解。 一、使用cmd下载 先用快捷键win R打开"运行"窗口,如下图。 在输入框中输入cmd并按回车Enter或点确定键,随后会出现这个画面: 输入pip install 你想下载的库名,并按回车&…...
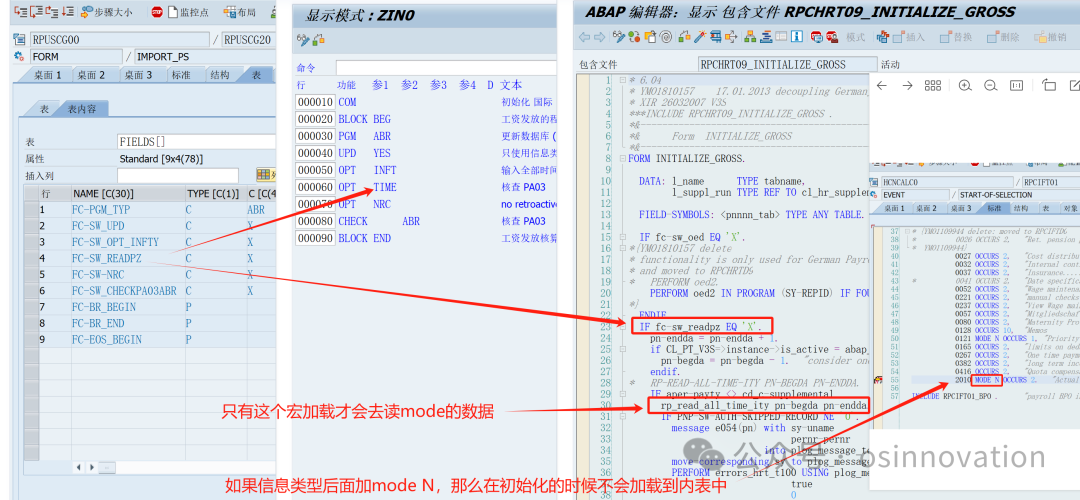
SAP HCM OPT函数作用
导读 INTRODUCTION OPT函数:SAP HCM工资核算是很多函数的汇总集,原有有兴趣问过SAP的人为什么SCHEMA需要这样设计,SAP的人说是用汇编的逻辑设计的,当时是尽可能用机器语言加速速度读取,每个函数都有对应的业务逻辑代码…...

Tensorflow音频分类
tensorflow https://www.tensorflow.org/lite/examples/audio_classification/overview?hlzh-cn 官方有移动端demo 前端不会 就只能找找有没有java支持 注意版本 注意JDK版本 package com.example.demo17.controller;import org.tensorflow.*; import org.tensorflow.ndarra…...
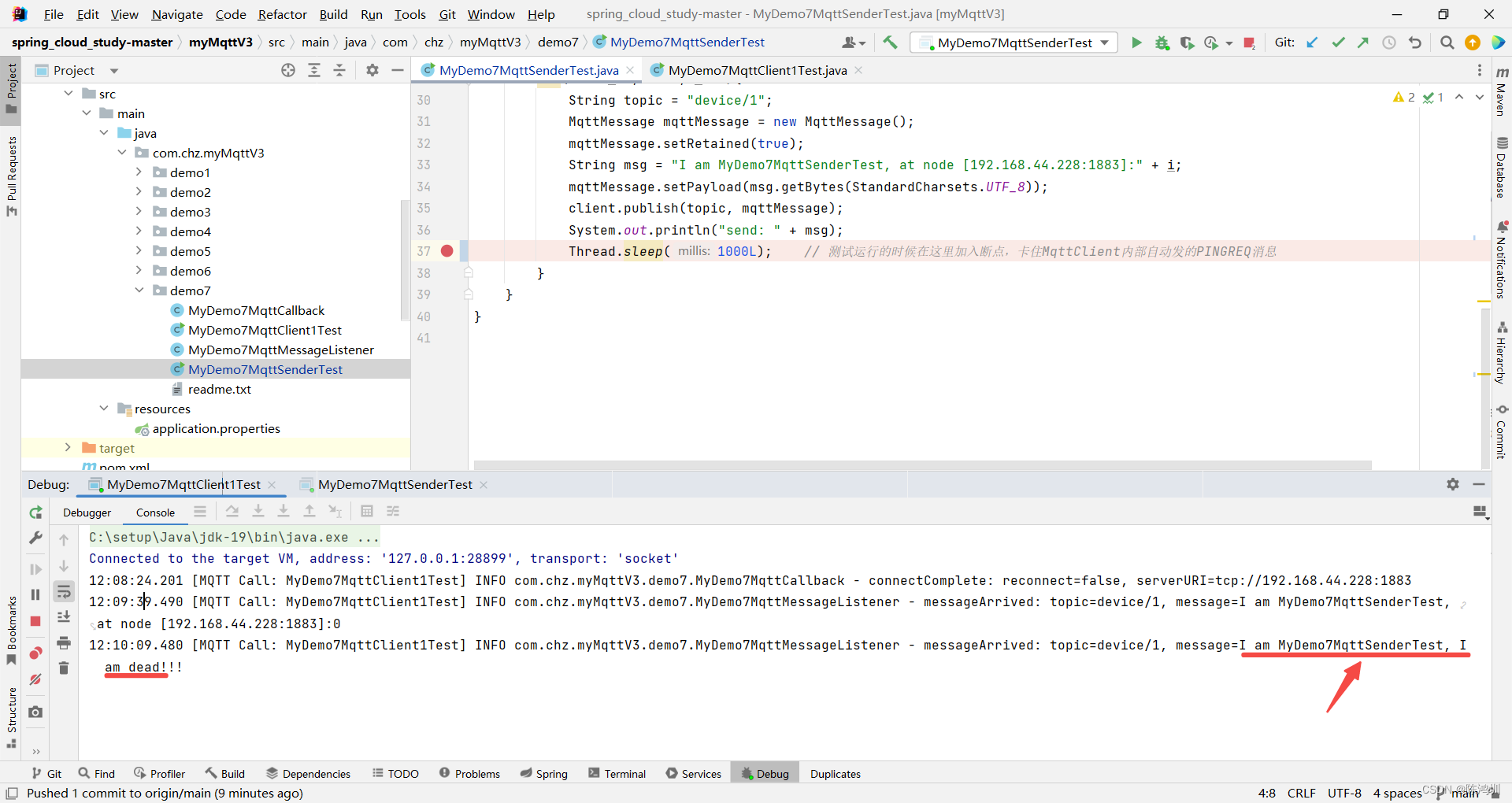
mqtt-emqx:keepAlive机制测试
mqtt keepAlive原理详见【https://www.emqx.com/zh/blog/mqtt-keep-alive】 # 下面开始写测试代码 【pom.xml】 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId><version>2…...

C++基础7:STL六大组件
目录 一、标准容器 1、顺序容器 vector 编辑 deque list 容器适配器 stack queue prority_queue: 关联容器 有序关联容器set、mutiset、map、mutimap 增删查O(log n) 无序关联容 unordered_set、unordered_mutiset、unordered_map、unordered_mutimap 增删…...

特别名词Test Paper1
特别名词Test Paper1 ability 能力abstract 摘要accountant 会计accuracy 准确度acid 酸action 行动activity 活动actor 男演员adult 成人adventure 冒险advertisements 广告,宣传advertising 广告advice 建议age 年龄agency 代理机构,中介agreement 同…...

每日题库:Huawe数通HCIA——全部【813道】
1.关于ARP报文的说法错误的是?单选 A.ARP报文不能被转发到其他广播域 B.ARP应答报文是单播方发送的 C.任何链路层协议都需要ARP协议辅助获取数据链路层标识 DARP请求报文是广播发送的 答案:C 解析: STP协议不需要ARP辅助 2.园区网络搭建时,使用以下哪种协议可以避免出现二层…...

#04 Stable Diffusion与其他AI图像生成技术的比较
文章目录 前言1. Stable Diffusion2. DALL-E3. GAN(生成对抗网络)4. VQ-VAE比较总结 前言 随着人工智能技术的飞速发展,AI图像生成技术已成为创意产业和科研领域的热点。Stable Diffusion作为其中的佼佼者,其性能和应用广受关注。…...
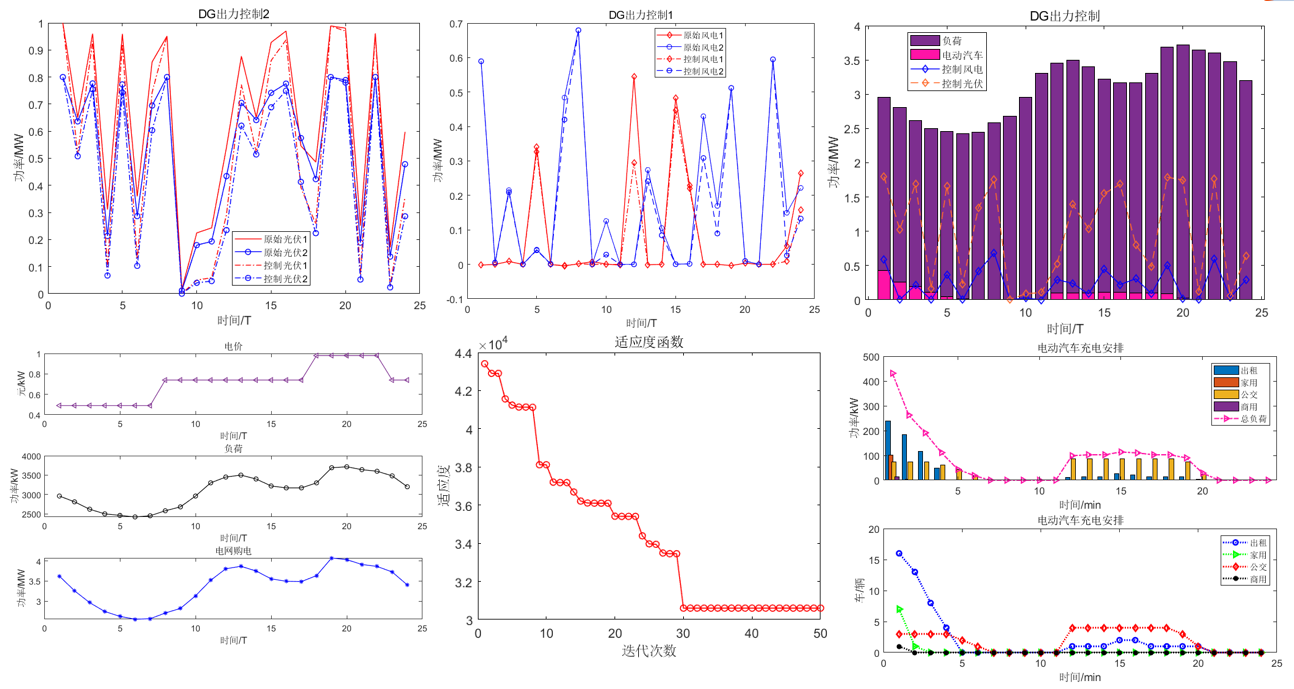
不确定性+电动汽车!含高比例新能源和多类型电动汽车的配电网能量管理程序代码!
前言 能源供应的可持续性和清洁性是当今世界共同关注的议题,配电网与可再生能源发电相结合,通过多能互补和梯级利用,在不同时空取长补短,提高能源利用率,减少温室气体排放,是解决能源短缺和环境问题的有效…...

准确-K8s系列文章-修改containerd 默认数据目录
修改 Kubernetes 集群中 containerd 默认数据目录为 /data/containerd 前言 本文档适用于 Kubernetes 1.24 及以上版本的集群,介绍如何将 containerd 默认的数据目录从 /var/lib/containerd 修改为 /data/containerd。 步骤 1. 停止 containerd 服务(…...

深入探索Linux命令:`aulastlog`
深入探索Linux命令:aulastlog 在Linux系统中,安全管理一直是管理员和用户关注的焦点。aulastlog是一个非常有用的工具,用于显示用户最近登录的日志。它通过分析/var/log/lastlog文件来提供这些信息,这个文件记录了系统上所有用户…...

Debezium日常分享系列之:Debezium 2.6.2.Final发布
Debezium日常分享系列之:Debezium 2.6.2.Final发布 一、新功能和改进1.Oracle 数据库查询过滤超过 1000 个表 二、修复和稳定性改进1.PostgreSQL 偏移刷新竞争条件2.Avro 兼容性 一、新功能和改进 1.Oracle 数据库查询过滤超过 1000 个表 Debezium Oracle 连接器允…...

PHP质量工具系列之phpmd
PHPMD PHP Mess Detector 它是PHP Depend的一个衍生项目,用于测量的原始指标。 PHPMD所做的是,扫描项目中可能出现的问题如: 可能的bug次优码过于复杂的表达式未使用的参数、方法、属性 PHPMD是一个成熟的项目,它提供了一组不同的…...
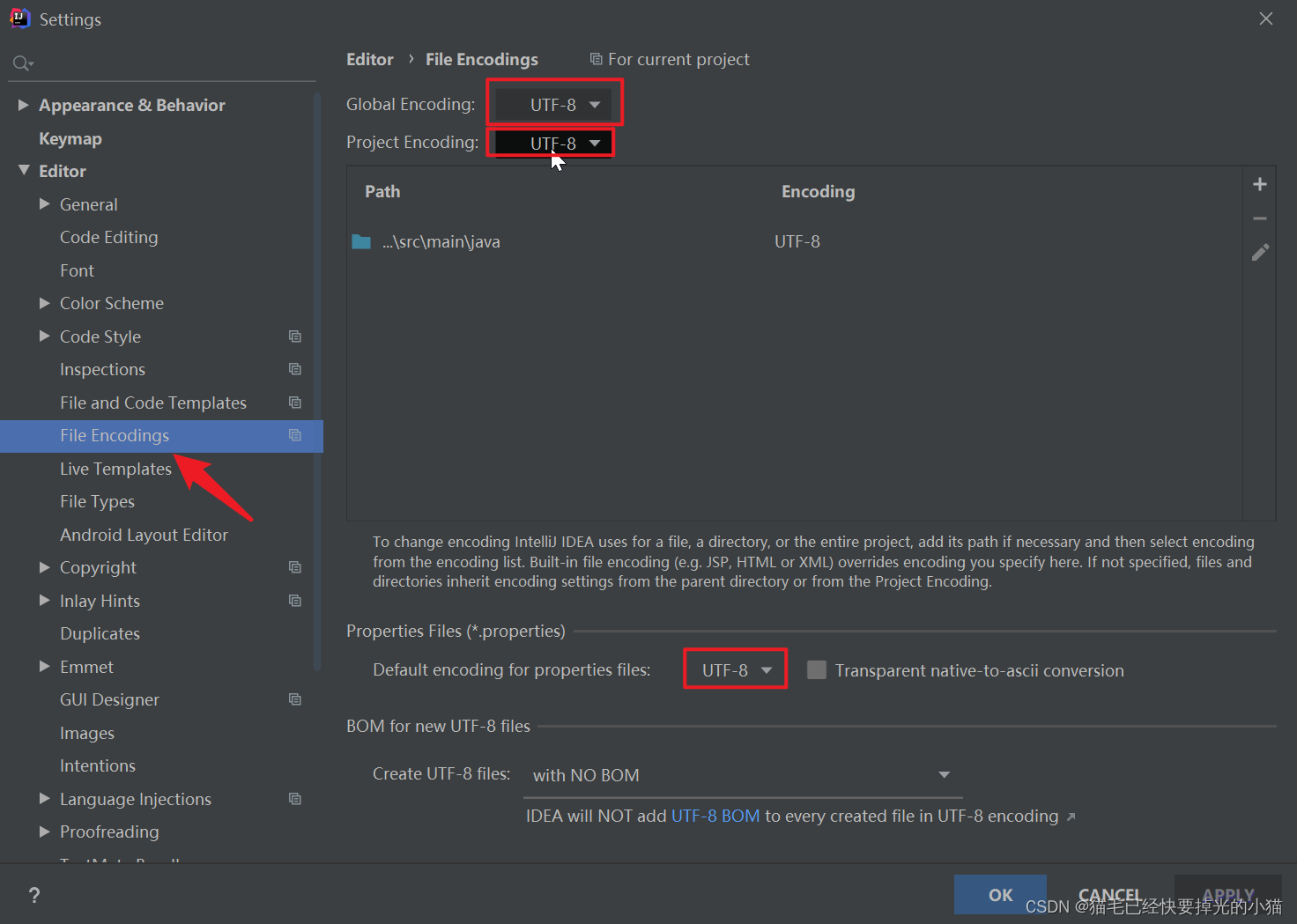
【java】速度搭建一个springboot项目
使用软件:IDEA,mysql 使用框架:springboot mybatis-plus druid 坑点 使用IDEA搭建一个springboot项目的时候,需要考虑一下IDEA版本支持的JDK版本以及maven版本。否则再构建项目,引入pom的时候就会报错。 需要检查…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
