离散数学---树

目录

1.基本概念及其相关运用

2.生成树

3.有向树

4.最优树

5.前缀码

---

1.基本概念及其相关运用

（1）无向树：连通而且没有回路的无向图就是无向树；

森林就是有多个连通分支，每个连通分支都是树的无连通的无向图；

树叶就是这个无向图里面的度数是1的节点，分支点就是度数大于等于2的节点，简单的讲就是没有其他的分支的顶点就叫做树叶，还可以从这个地方继续细分的顶点就叫做分支点；

（2）无向树的特点

无向树的三个特点，边数等于顶点数减去1，连通而且没有回路；

（3）随堂测验：对于无向树的进一步理解

无向树的任意的一条边都是桥（就是割边）；任意的两个不同的节点之间只有一条路径可以抵达（因为无向树里面要求是没有回路，如果有第二条路径可以抵达不就是构成回路了，这样的话就不满足这个无向树的定义了），无向树就是一个简单图，不相邻的节点之间添加一条边就会形成初级的回路；

 实际问题：求解这个树叶的数量，我们需要用到握手定理，就是度数和等于边数的两倍，边的数量根据  边数等于顶点数减去1  这个等量关系得出，最后根据握手定理进行求解，反正就是要用到这个无向树的性质和握手定理求解树叶的个数；

（4）实战演练

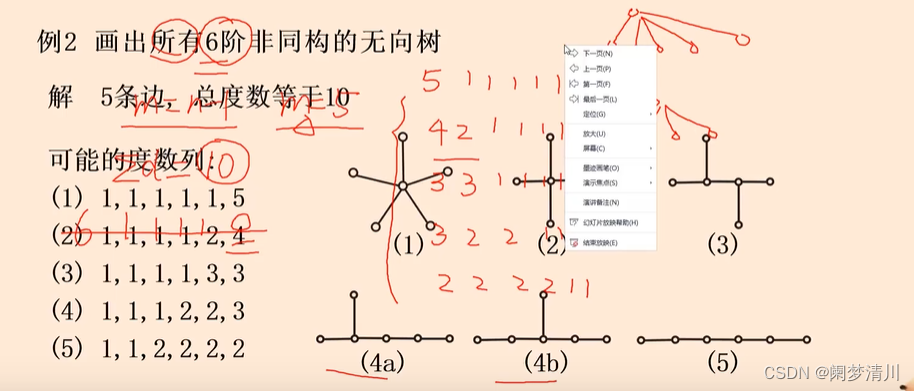
这个试画出六阶的无向树，这个六阶的表示是这个树有6个顶点，根据这个定理，无向树里面的边数等于顶点数减去1，说明这个无向树是有5条边，我们在根据这个握手定理，就可以的出来这个 无向树的度数和就是边数的两倍，也就是10，这个时候我们再进行列举所有的可能会出现的情况，因为是6个顶点，最大的数字度数就只能是5，否则就会出现重边和环，不满足这个无向树的定义了，其中的第四种情况是可以画出来两种可能的情况的；

这个就是利用握手定理，度数和等于边数的两倍，边数等于顶点数减去1，利用这两个等量关系就可以基本上解决这个无向树里面的所有的相关问题；在这个等量关系里面，边数是发挥了桥梁的作用，因为这个边数是顶点数减去1，边数的两倍就是度数和，边数这个变量把握手定理和无向树里面的定理给串联了起来；

（5）综合练习

树都是二部图，这个是没有问题的，因为这个二部图的判定定理就是没有奇数圈，而我们的数是不会有回路的，所以肯定就没有圈，肯定是满足二部图的定义的；

哈密顿图的定义就是经过所有的节点返回，判定定理就是这个没有奇度数的顶点，这个时候我们的数如果有树叶的话，肯定是有奇度数的顶点的，不一定是欧拉图；树里面的平凡树是哈密顿图，也是欧拉图，其他的数都不是哈密顿图和欧拉图；

平面图的要求就是不交叉，这个树肯定不会交叉，我们正常情况下去画一棵树都是不会交叉的，Krs就是一个二部图，rs分别表示的是两个不同的集合里面的节点的个数，k10就是一个数，只有一片树叶的树，k11和k12都是树，所以这个krs有的是树，有的不是树；

2.生成树

（1）生成树和余树

对于右边的一个平面图，包括这个红色的和黑色的，如果这个平面图的生成子图是一棵树，我们就把这个生成子图叫做这个平面图的生成树，生成树里面涉及到这个平面图里面的边我们叫做数值，没有包括到生成树里面的边我们叫做弦，这些弦组成的图形叫做余树；

什么是生成子图，首先这个生成子图肯定是一个平面图的子图，这个是很明显的，其次生成子图还需要满足这个生成子图需要包括这个原来的平面图上面的所有的顶点，而且没有重边，没有环；实际上对于一个图而言，是可以有很多个生成子图的，所以一个连通图可以有很多个不同的生成树；

虽然这个生成子图剩下的弦的集合叫做余树，但是这个并不是真正的树，因为显然这个余树是不联通的，不符合树的定义； 

（2）最小生成树

我们上面介绍的生成树是可能有多个的，这些情况里面的这个权重最小的就是最小生成树，最小生成树同样也不是唯一的；

这个求解最小生成树的算法有这个避圈法，这个方法的主要逻辑就是躲避开所有的圈，按照从小到大的权重进行相应的排列，不能形成圈，满足这个树的定义；

3.有向树

（1）有向树就是指那些不关注方向的情况下，这个是一棵树，我们就可以称之为有向树；

有向树里面有这个根数（只有一个入度是0的顶点，其余的顶点的入度是1），这个入度是0的顶点我们称之为树根；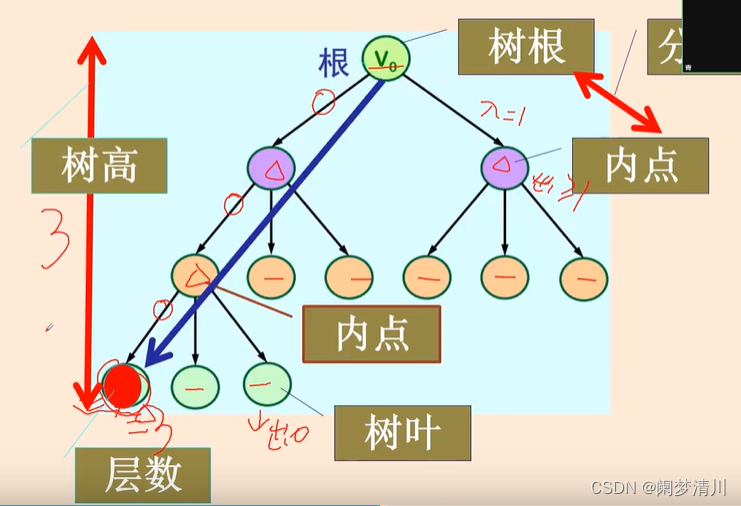

这个树根就是这个图里面的最上面的那个点，出度是0的节点我们称之为树叶，出度大于等于1 的节点我们叫做内点，内点和树根就组成了这个分支点，这个树高和树的层数也是我们关注的，这个定义和我们在数据结构里面的定义是有所区别的，我们这里定义的树高指的就是从根树开始经过的边的个数 ，所以这个图里面的红色节点的层数就是3，因为这个树根只需要经过三条边就可以到达这个节点的位置；

（2）根树的分类

（3）随堂演练

这个题目上面的五元正则树表示这个树如果有子节点那么就必须要有5个子节点，我们根据题目的要求画出这个正则树，分支点就是这个树根和内点的总称，这个图里面有1个树根，两个内点，所以这个分支点的个数就是3个；

 （4）根树的相关证明

这个二元正则树就是如果有节点，需要有两个节点，第一个证明就是用的握手定理和这个边数，树叶数和这个顶点数之间的转换，我们需要先画出来这个已知的图形，射出一个变量n表示这个树的顶点的数量，根据这个握手定理，树根的度是2，树叶的度是1，剩下的这个内点的个数就是n-1-t，其中这个里面1表示的就是树根，t就是这个树里面的树叶的数量，剩下的就是内点，一个内点的度是3，因此我们就可以根据这个度数等于边数的两倍列方程，m=n-1联立即可求解；

r元正则树其实是一样的逻辑，就是这个内点的度数是r+1，i-1求出来的就是这个内点的数量，第一个r表示的就是这个树根的度数，第三个t表示的就是所有的树叶的度数和；

我们通过这连个证明就可以发现，只要是相关的题目，必须同时拥有边数和顶点数这两个变量，第一个是给出来了边数，我们需要自己设一个变量n表示顶点数，第二个是给出了分支节点的个数，树叶的个数，实际上就是给出了所有的节点的个数，我们需要定义一个变量m表示边数；

4.最优树

（1）权重乘上对应的长度，求和就是该带权二叉树的权（这里的权重求和并不是这个树上面的所有节点，而是树叶节点），在所有的二叉树里面，权值最小的我们称之为最优二叉树；

（2）哈夫曼算法求解最优树问题

这个算法就是在原来的权重集合的基础上面，不断的更新这个权重，让这个最小的两个权重组成新的 权重集合，不断的更新这个分支节点和树叶，直到形成一个完整的树为止；

 （3）算法运用

这个题目就是哈弗曼编码的一个应用，题目上面给出的就是出现的权重 和对应的频率，我们就是根据这个频率的大小进行排序的，首先按照从小到大的顺序进行排列，选出来这个权重最小的59组成14，重新对于这个权重集合进行排序，再从这个剩下的5个权重里面选择最小的12和13相加得到25，再对于这个集合重新排列，接下来就是把这个14 16组成新的权重，依次进行下去，直到形成最终的最优树为止；

实际上我们可以发现这个最优树上面除了我们的权重之外，还有这个01这些标识，这个就是我们接下来要介绍的前缀码的知识；

5.前缀码

（1）相关定义

前缀码就是一个集合里面的某些元素是不是其他某个元素的前缀码，这个如果是的话，就会出现歧义的现象，因此这个我们把如果这个集合里面没有一个序列是另外的一个序列的前缀，我们就把这样的序列结合叫做前缀码； 

（2）前缀码的定理

这样我们学习了前缀码之后，就可以使用这个前缀码解决上面的问题了，这个01就是一种二叉的标识，我们根据这个就可以写出任意的二叉树的前缀码，同理，我们根据任意的一个前缀码都是可以画出这个与之对应的二叉树的；

（3）实际应用

 

 

 上面的这个就是一个实际的问题，通信里面的八进制的不同的数字的使用的次数是不一样的，这个是用我们使用哈夫曼算法对于这个问题求解他的最优树，他的百分比就可以理解为这个对应的权重，按照上面的方法不断地合并，并对于这个新的序列集合排序，得到了这个最优树，我们通过这个树叶节点的权重乘上对应的层数（从树根开始到这个节点的经过的边数）得到的就是285，平均下来的一个就是2.85,我们如果想要传输10的n次方数据，就需要二进制数字2.85*10的n次方个，但是使用等长码就需要3*10的n次方个，这个也显示出来我们使用哈夫曼编码的优势；

通过上面的例子，我们也可以知道对于这个不同的数字，在于我们的日常使用中的频率是不一样的，在这个最优二叉树里面，我们经常使用的数字靠近树根，而且这个前缀码简洁，那些不是很经常使用的数字就远离这个树根，而且对应的前缀码就会比较复杂，这个也是变长编码的一大特点。