【数据结构】平衡二叉树左旋右旋与红黑树

平衡二叉树左旋右旋与红黑树

平衡二叉树

定义

平衡二叉树是二叉搜索树的一种特殊形式。二叉搜索树（Binary Search Tree，BST）是一种具有以下性质的二叉树：

1. 对于树中的每个节点，其左子树中的所有节点都小于该节点的值。
2. 对于树中的每个节点，其右子树中的所有节点都大于该节点的值。
3. 左子树和右子树都必须是二叉搜索树。

而平衡二叉树（Balanced Binary Tree）在满足了二叉搜索树的所有性质的基础上，还额外保证了树的高度尽可能小，即任意节点的左右子树高度差不超过1。

举例

以下是平衡二叉树的几个例子：

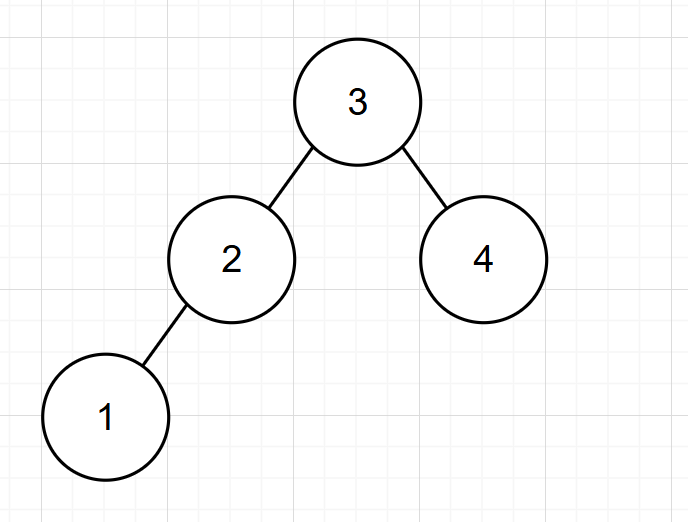
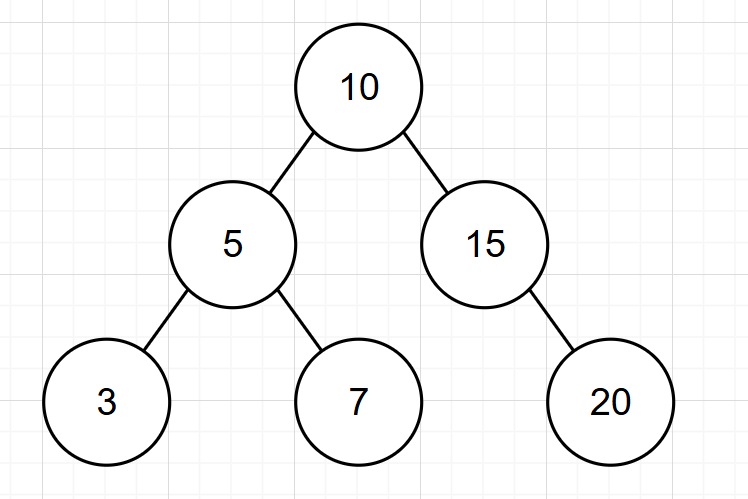
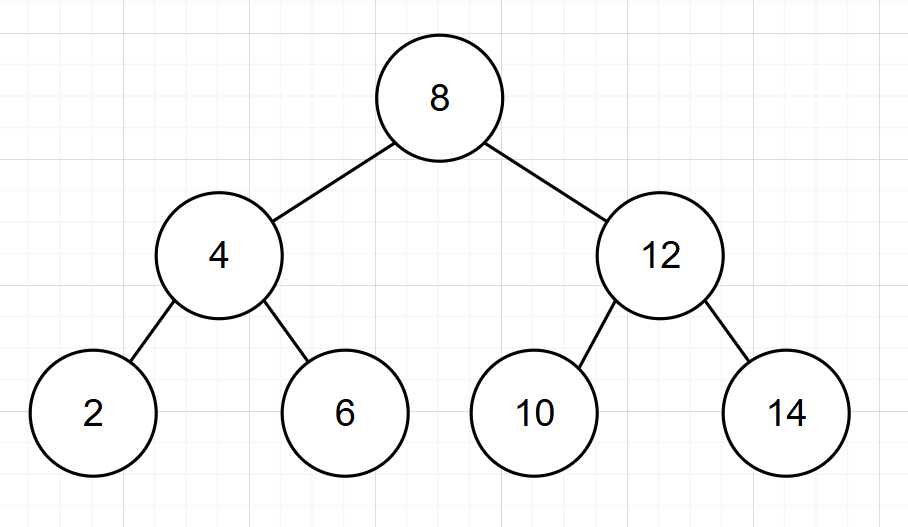
旋转机制

平衡二叉树通过旋转操作来保持其平衡性。旋转操作主要有两种类型：左旋转和右旋转。这些旋转操作通常应用于AVL树和红黑树等平衡二叉树的调整过程中。

左旋转：左旋转是一种操作，将一个节点的右子节点提升为新的根节点，原来的根节点成为新根节点的左子节点。左旋转的目的是减小树的整体高度，以维持平衡。

右旋转：右旋转是一种操作，将一个节点的左子节点提升为新的根节点，原来的根节点成为新根节点的右子节点。右旋转的目的也是减小树的整体高度，以维持平衡。

触发时机：当添加一个节点之后，该树不再是一颗平衡二叉树

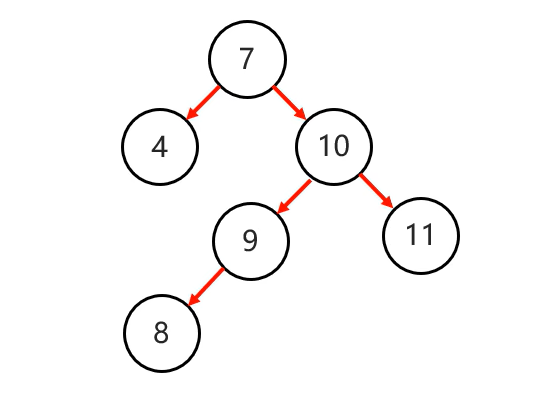
左旋

当我们想给

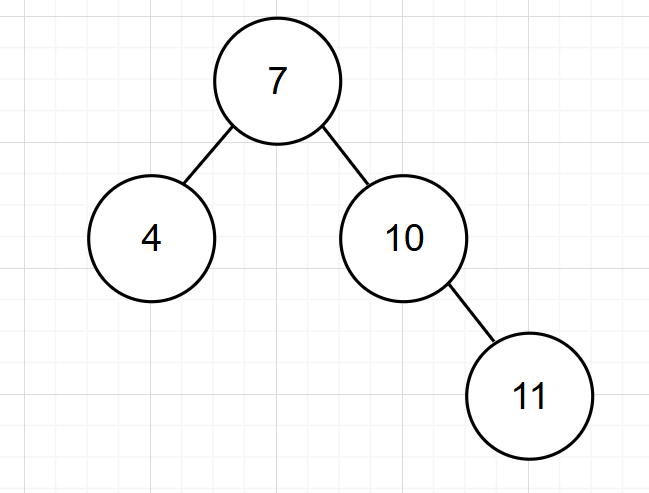
这个二叉树中插入一个新的节点12，这个平衡二叉树就会变为：

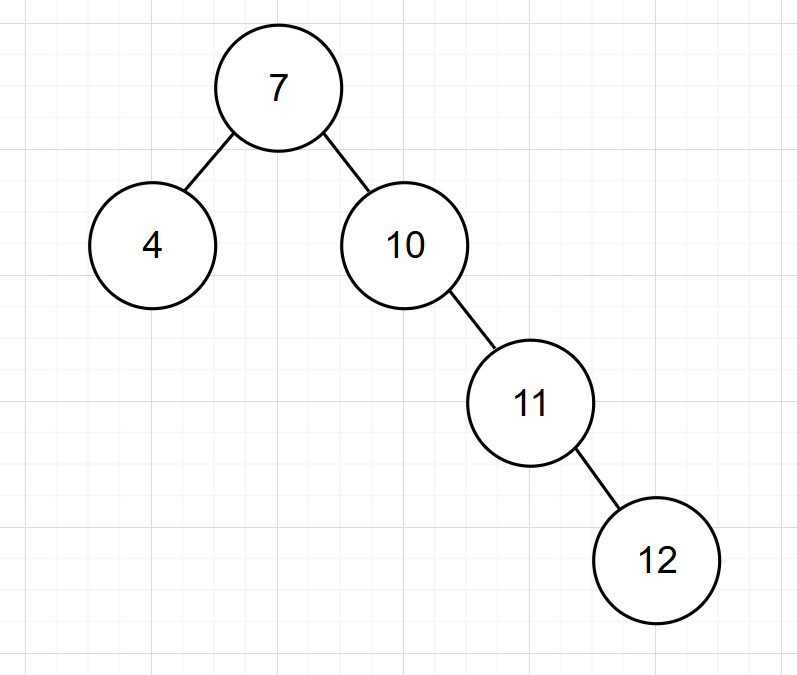
此时我们就会发现二叉树不平衡了，为了重新平衡，我们就需要进行旋转了。

为了进行旋转，我们需要去寻找支点：从添加的节点开始，不断的往父节点找不平衡的节点

这里我们从节点12开始往上找：

1. 节点11：平衡
2. 节点10：不平衡

所以节点10为支点！！

左旋的步骤：

1. 以不平衡的点作为支点
2. 把支点左旋降级，变成左子节点
3. 晋升原来的右子节点

旋转后的二叉树为：

---

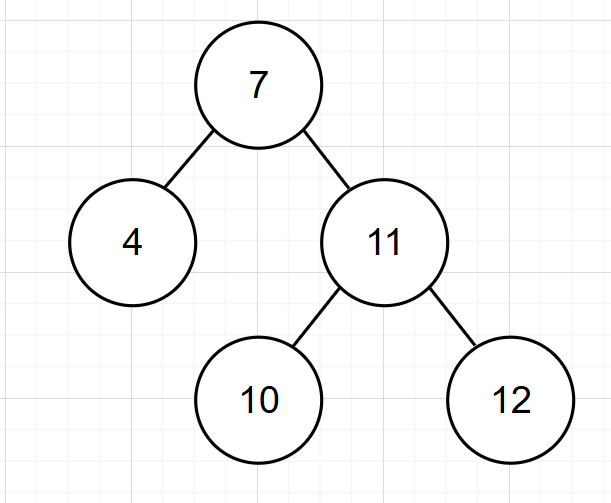
​ 以上为较为简单的左旋，下面为较为复杂的左旋

---

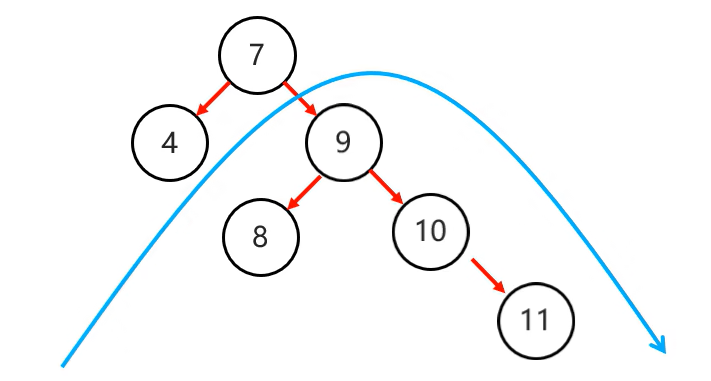
已知二叉树（不平衡）：

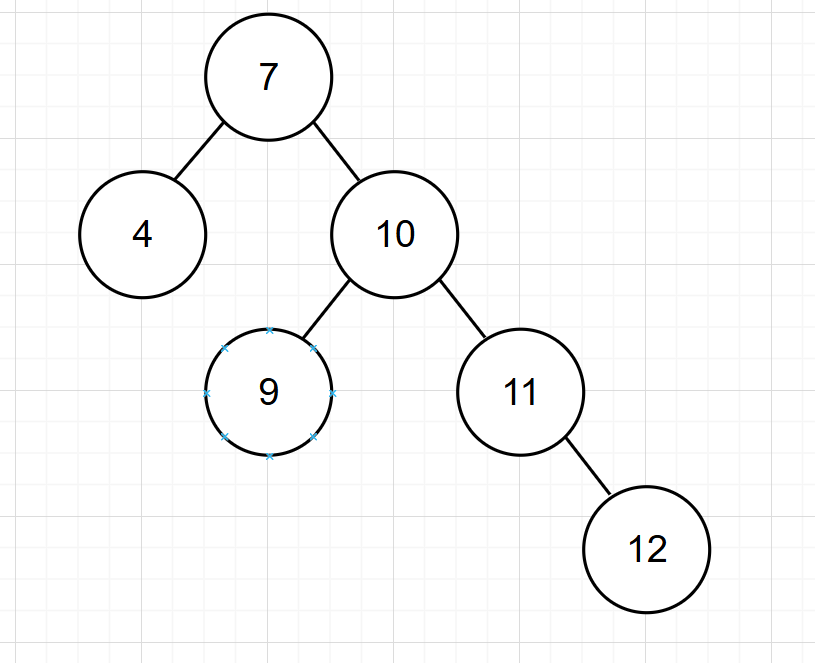
还是需要从添加的节点向上找不平衡的节点

1. 节点11：平衡
2. 节点10：平衡
3. 节点7：不平衡

节点7为支点

而此时旋转的步骤和刚才的就有所不同了：

1. 以不平衡的点作为支点
2. 将根节点的右侧往左拉
3. 原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点

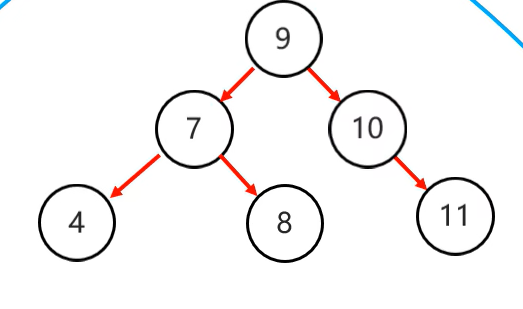
在上面的二叉树中，多余的节点为节点9（节点9为节点10的左子结点很重要）。

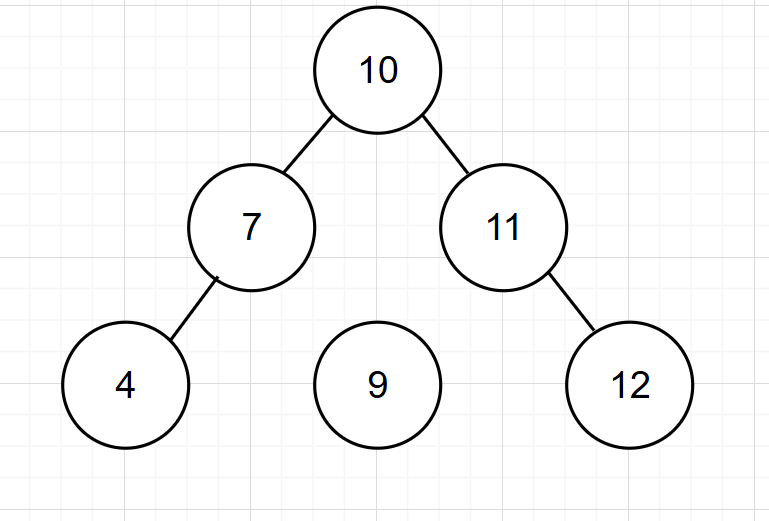
下面为具体步骤：

1. 先将节点9（多余的左子节点）分离：

   

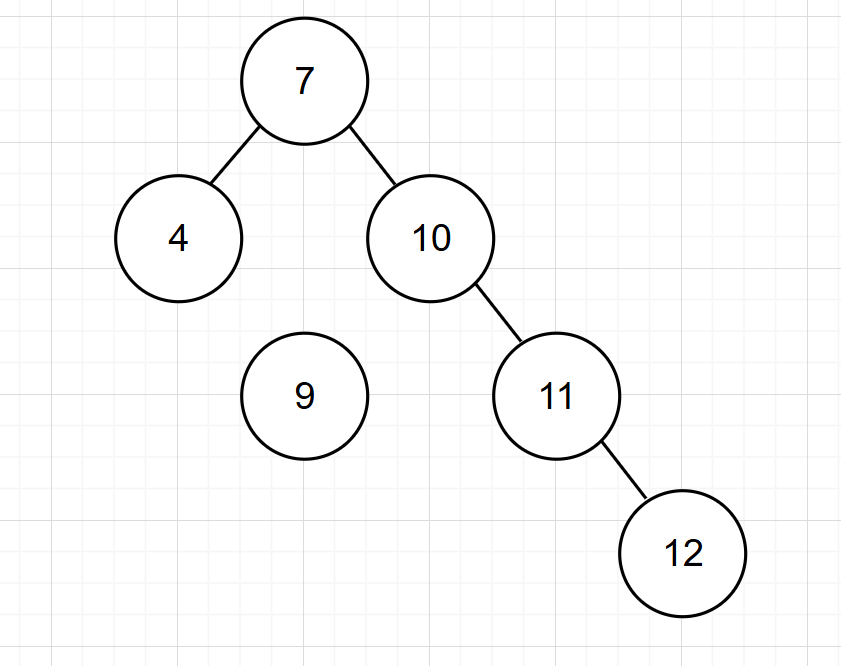
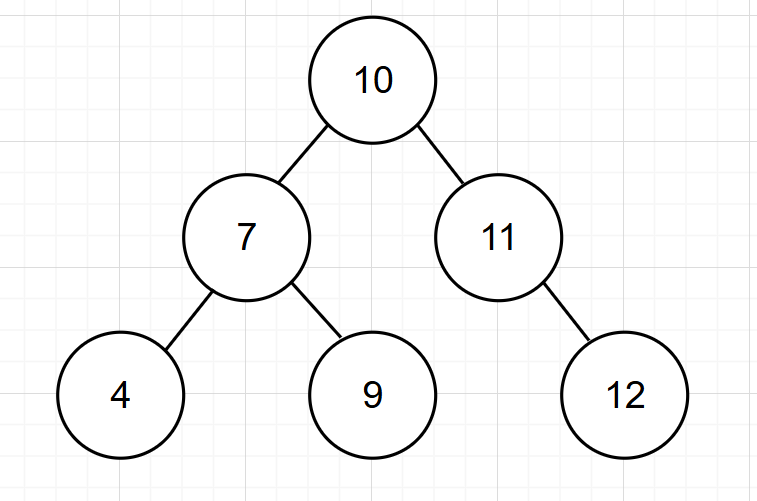
2. 以节点7为支点进行左旋：

   

3. 将多余的节点进行分配

   因为节点9之前为节点10的左子结点，所以此时9节点应该继续接才节点10的左边，此处应该放在节点7的右节点上

右旋

右旋与左旋在处理上是类似的，就不再粘贴图示了

步骤

1. 以不平衡的点作为支点
2. 就是将根节点的左侧往右拉
3. 原先的左子节点变成新的父节点，并把多余的右子节点出让，给已经降级的根节点当左子节点

需要旋转的四种情况

1.左左（一次右旋）

当根节点左子树的左子树有节点插入，导致二叉树不平衡

有两种添加情况：

以节点7为根节点

我们只需要进行一次右旋就可以了：

2.左右（两次旋转）

当根节点左子树的右子树有节点插入，导致二叉树不平衡

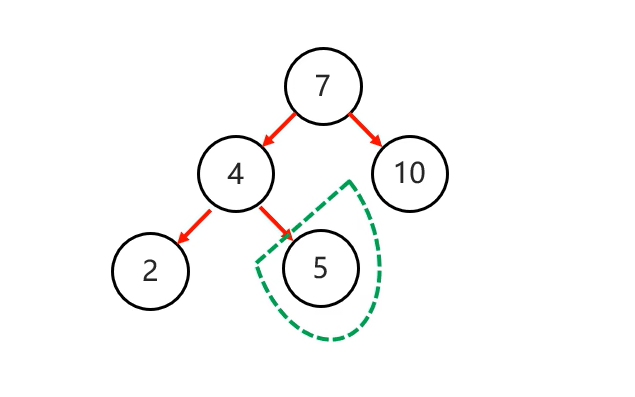
添加节点：

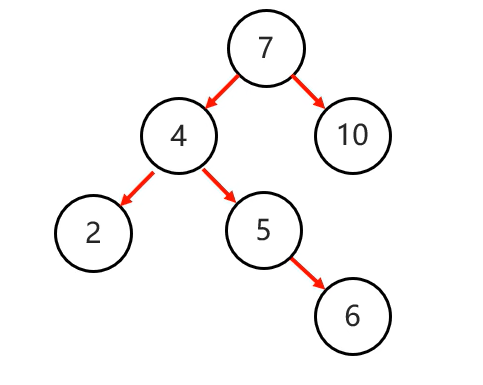
此时仅仅一次右旋就不能实现平衡了。

我们需要先一4为支点，先局部左旋，再整体右旋就可以实现了：

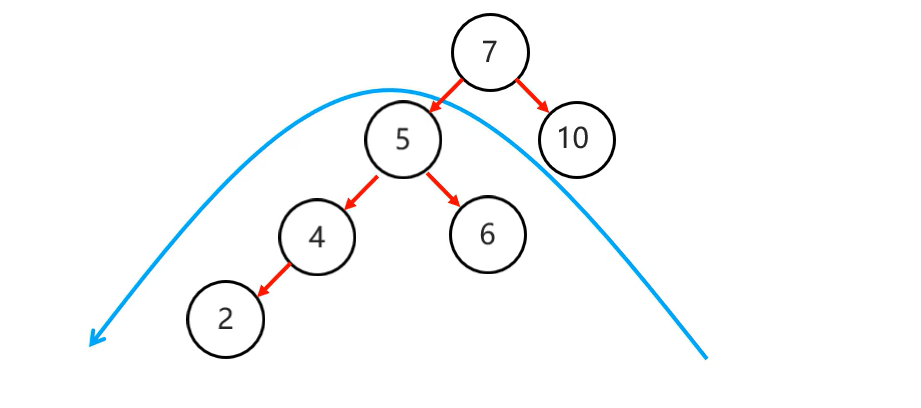
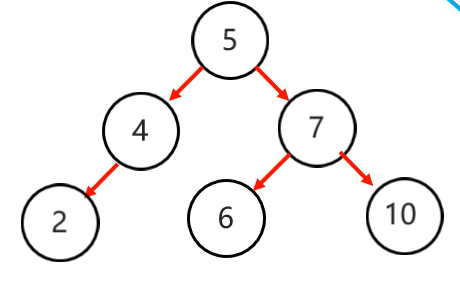
3.右右（一次旋转）

当根节点右子树的右子树有节点插入，导致二叉树不平衡

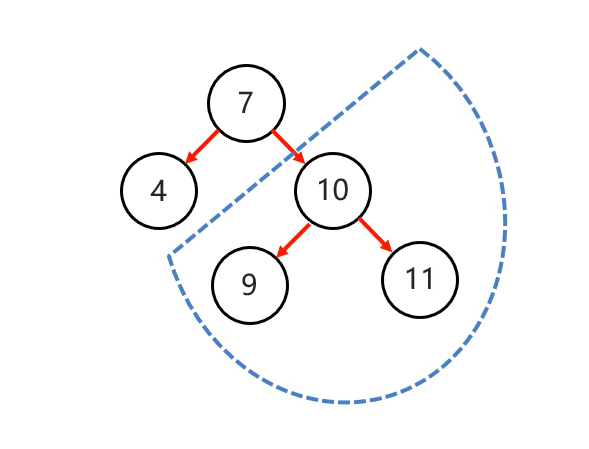
添加节点12：

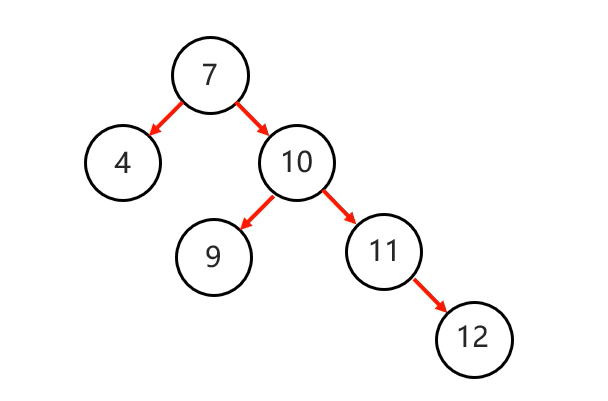
以节点7为支点进行左旋一次就能实现平衡：

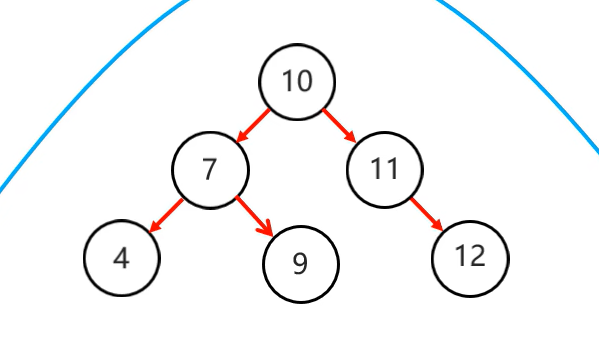
4.右左（两次旋转）

当根节点右子树的左子树有节点插入，导致二叉树不平衡

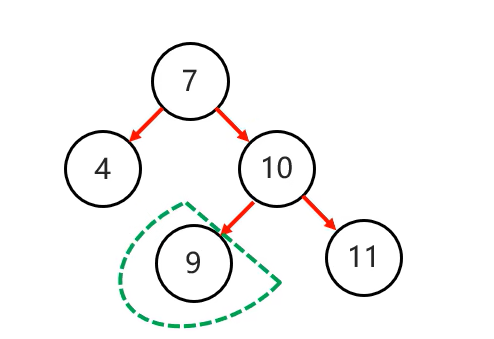
添加节点8：

先局部右旋再整体左旋：

红黑树

• 红黑树是一种自平衡的二叉查找树，是计算机科学中用到的一种数据结构。
• 1972年出现，当时被称之为平衡二叉B树。后来，1978年被修改为如今的"红黑树"
• 它是一种特殊的二叉查找树，红黑树的每一个节点上都有存储位表示节点的颜色
• 每一个节点可以是红或者黑;红黑树不是高度平衡的，它的平衡是通过"红黑规则"进行实现的

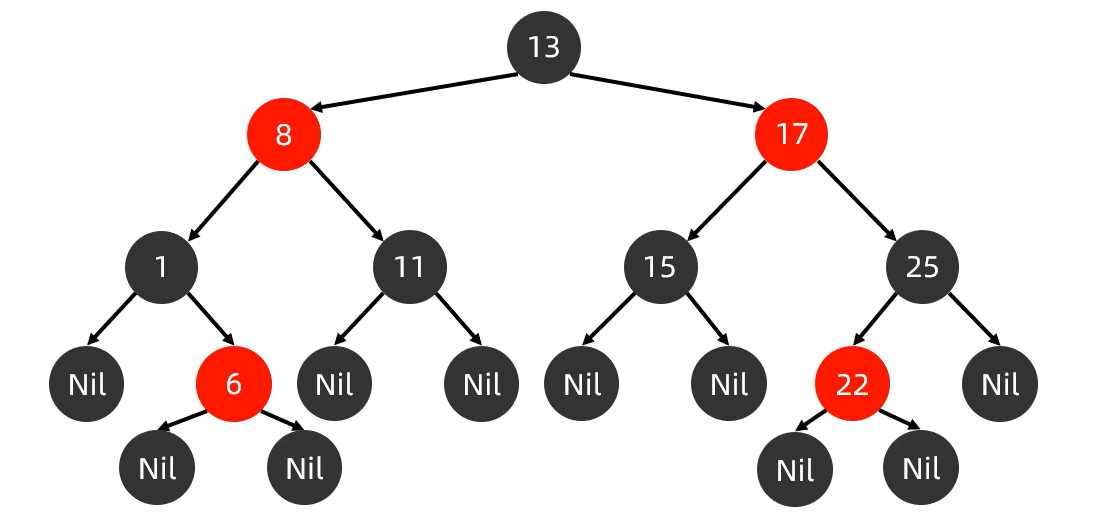
红黑规则

1. 每一个节点或是红色的，或者是黑色的
2. 根节点必须是黑色
3. 如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nǐl，这些Nil视为叶节点，每个叶节点(Nil)是黑色的
4. 如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
5. 对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点

添加节点规则

默认颜色：添加节点默认是红色的(效率高)

举例

假设我们需要添加三个节点：20，18，23

1.假设三个节点都是黑色的

先添加节点20：

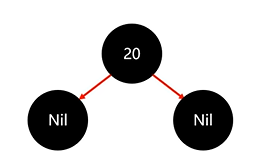
然后添加节点18：

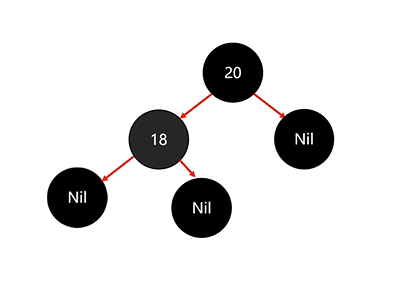
此时我们发现我们的红黑树已经违背了红黑规则（第五条规则）

如果我们把节点18变为红色，则就满足了红黑规则：

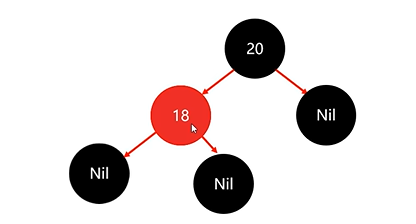
下来存节点23：

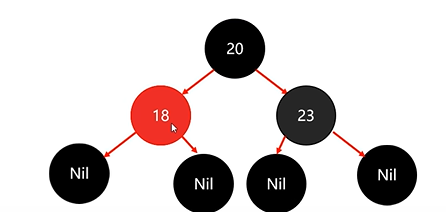
依旧违背红黑规则，将23变为红色：

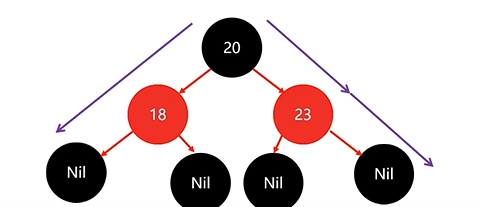
一共调整了两次节点颜色

2.假设节点颜色都为红色：

那么先添加节点20：

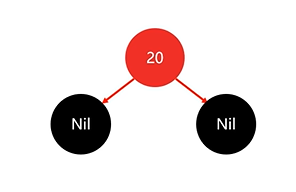
违背了规则2

将节点变为黑色后，插入节点18：

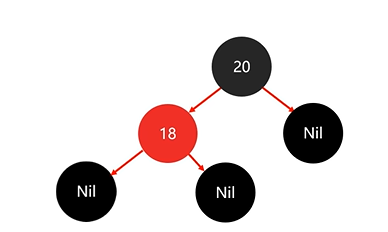
并没有违背红黑规则，不需要调整

下来添加节点23：

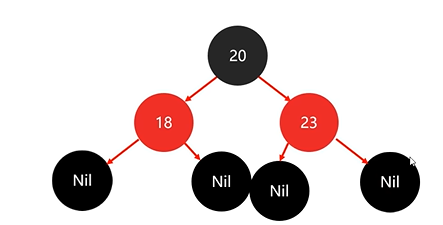
依然不需要调整。

一共调整了一次节点颜色

所以我们得出结论：默认颜色：添加节点默认是红色的(效率高)

小结

本篇博客到这里就结束了，如果有错误麻烦大家指正，感谢阅读！

已经到底啦！！！