2024年全国一高考数学压轴题

(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n + 2 } \{a_{1},...,a_{4n+2}\} {a1,...,a4n+2} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去掉第 i i i 和 j j j 项后, 若一个分割方案把 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} 分割成 n n n 个长为4的等差数列, 那么该分割方案也必然把 { a 1 , . . . , a 4 n + 2 } \{a_{1},...,a_{4n+2}\} {a1,...,a4n+2} 分割成 n n n 个长为4的等差数列, 因此二者等价.
考虑使得 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} ( i , j ) (i,j) (i,j)-可分的 ( i , j ) (i,j) (i,j) 的可行取值数目:
当 n = 1 n=1 n=1 时, 通过穷举, ( i , j ) (i,j) (i,j) 可取 ( 1 , 2 ) (1,2) (1,2), ( 1 , 6 ) (1,6) (1,6), ( 5 , 6 ) (5,6) (5,6). 当 n = k n=k n=k 时, 设 ( i , j ) (i,j) (i,j) 有 x k x_k xk 个可行取值, 考虑当 n = k + 1 n = k+1 n=k+1 时: { 1 , . . . , 4 k + 6 } \{1,...,4k+6\} {1,...,4k+6} 的前 4 4 4 项和后 4 k + 2 4k+2 4k+2 项分别构成两个等差数列. 由此易知, 将 n = k n=k n=k 时的每个 ( i , j ) (i,j) (i,j) 可行取值整体加 4 4 4, 就构成了当前的一个可行取值. 容易验证, 每个 i , j > 4 i,j>4 i,j>4 的可行取值都可以视为这么得到的. 接下来我们考虑 i < 4 i<4 i<4 的可行取值. 依然是枚举, 令 i i i 取 1 1 1, j j j 取 ( 1 , 4 s + 2 ) (1, 4s+2) (1,4s+2), 其中 0 ≤ s ≤ n 0\leq s \leq n 0≤s≤n, 此时 i i i, j j j 之间的数的个数为 4 4 4 的整数倍, j + 1 j+1 j+1 到 4 n + 2 4n+2 4n+2 之间数的个数为 4 4 4 的整数倍, 显然这个 ( i , j ) (i,j) (i,j) 的取值是可行的, 即 ( 1 , 4 s + 2 ) (1, 4s+2) (1,4s+2), 0 ≤ s ≤ n 0\leq s \leq n 0≤s≤n 是可行的. 设 2 ≤ d ≤ n 2\leq d\leq n 2≤d≤n, 则 1 1 1 到 4 d 4d 4d 刚好可以分成 d d d 个长度为4的等差数列 { 1 , . . . , 1 + 3 d } \{1,...,1+3d\} {1,...,1+3d}, { 2 , . . . , 2 + 3 d } \{2,...,2+3d\} {2,...,2+3d}, …, { d , . . . , 4 d } \{d,...,4d\} {d,...,4d}, 2 + 4 d 2+4d 2+4d 与 4 d 4d 4d 之间刚好隔了一个数 4 d + 1 4d+1 4d+1, 去除 2 2 2 和 4 d + 1 4d+1 4d+1, 1 1 1 到 4 d + 2 4d+2 4d+2 也可以分成 d d d 个长度为 4 4 4 的等差数列 { 1 , . . . , 1 + 3 d } \{1,...,1+3d\} {1,...,1+3d}, { 2 + d , . . . , 2 + 4 d } \{2+d,...,2+4d\} {2+d,...,2+4d}, …, { d , . . . , 4 d } \{d,...,4d\} {d,...,4d}. 令 i i i 取 2 2 2, j = 4 d + 1 j=4d+1 j=4d+1, 则去除 i i i 和 j j j 后 1 1 1 到 4 d + 2 4d+2 4d+2 也刚好可以分成 4 4 4 个长度为 4 4 4 的等差数列, 剩下的数相邻四个为一组可以分成长度为 4 4 4 的若干等差数列, 所以此时的 ( i , j ) (i,j) (i,j) 取值是可行的, 即 ( 2 , 4 d + 1 ) (2, 4d+1) (2,4d+1), 2 ≤ d ≤ n 2\leq d \leq n 2≤d≤n 是可行的. 因此 n = k + 1 n=k+1 n=k+1 时的可行取值数目至少为 x k + 1 = x k + 2 k + 2 x_{k+1}=x_k+2k+2 xk+1=xk+2k+2. 递推可得 x k + 1 ≥ 3 + 2 ( 1 + . . . + k ) + 2 k = k 2 + 3 k + 3 x_{k+1} \geq 3+2(1+...+k)+2k=k^2+3k+3 xk+1≥3+2(1+...+k)+2k=k2+3k+3.
综上, 尽管没求出可行取值的具体数目, 但可知其下界为 n 2 + n + 1 n^2+n+1 n2+n+1. 使得数列 { a 1 , . . . , a 4 m + 2 } \{a_1,...,a_{4m+2}\} {a1,...,a4m+2} ( i , j ) (i,j) (i,j)-可分的 ( i , j ) (i,j) (i,j) 可行取值数目至少为 m 2 + m + 1 m^2+m+1 m2+m+1. 所以随机抽取两个 1 1 1 到 4 m + 2 4m+2 4m+2 的数 ( i , j ) (i, j) (i,j), 其使得 { a 1 , . . . , a 4 m + 2 } \{a_1,...,a_{4m+2}\} {a1,...,a4m+2} ( i , j ) (i,j) (i,j)-可分的概率至少为:
m 2 + m + 1 ( 2 m + 1 ) ( 4 m + 1 ) = m 2 + m + 1 8 m 2 + 6 m + 1 > 1 8 \frac{m^2+m+1}{(2m+1)(4m+1)}=\frac{m^2+m+1}{8m^2+6m+1}\gt \frac{1}{8} (2m+1)(4m+1)m2+m+1=8m2+6m+1m2+m+1>81
PS: 不是数学专业的… 只是喜欢数学的工科生而已. 没做出来, 想到了用数学归纳法做, 但是令 i = 2 i=2 i=2的时候, 试出来 j = 5 j=5 j=5是不可行的, 13 + 12 n 13+12n 13+12n 是可行的, 所以认为是隔 12 12 12 一个, 没想到5只是一个特例而已, 实际上9之后就可以, 被误导了方向, 他如果第二问是让证 ( 2 , 9 ) (2,9) (2,9) 或许就做出来了. 本16届表示上学的时候压根没见过这样的题, 而且现在选修三选一怎么没了?
相关文章:

2024年全国一高考数学压轴题
(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n 2 } \{a_{1},...,a_{4n2}\} {a1,...,a4n2} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n 2 } \{1,...,4n2\} {1,...,4n2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去…...

springboot+vue前后端项目接口校验通信数据完整性
方案:使用国密SM3算法实现数字签名 服务端 maven的pom文件引用 <!-- 国密算法支持 --><dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15to18</artifactId><version>1.69</version><…...

进程通信(IPC-Inter Process Communication)
进程之间的通信通过内核空间实现 IPC技术 ①管道(匿名管道/命名管道-FIFO队列) ②System V IPC(消息队列、信号量和共享内存) ③套接字(UNIX套接字&Internet套接字) ※信号 软中断,信号提供了一种处理异步事件的方法,作为进程通信的一种机制&am…...
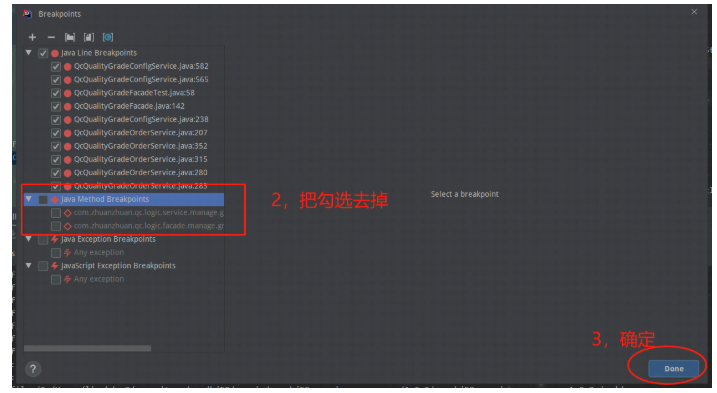
idea debug时提示”Method breakpoints may dramatically slow down debugging“的解决办法
问题现象 今天同事喊我过去看一个问题,项目正常启动的时候没问题,debug模式就卡住了,很久不动。我推测是哪个断点导致的,一看断点果然有情况。在方法上打了断点。 解决方式(Android Studio一样的解决) 1、View Brea…...
计算机缺失msvcp100.dll如何解决?教你5种简单高效的修复方法
在现代科技发展的时代,计算机已经成为我们生活和工作中不可或缺的工具。然而,在使用计算机的过程中,我们常常会遇到各种问题和困扰。其中之一就是计算机找不到msvcp100.dll文件。这个问题可能会给我们的生活和工作带来很多不便,下…...

对硬盘的设想2:纸存,硬指针,软指针
“纸存”是设想中的存储器,它只能改写两次:写一次,再改一次,然后就不能再动了。就像拿着钢笔在纸上写字一样,所以叫纸存。 硬指针P、软指针S S abcd S aPcdPx P aPcdPx S aycd ①一个软指针S,指向数据abcd…...

Python在股票交易分析中的应用:布林带与K线图的实战回测
引言 在股票交易的世界中,技术分析是投资者们用来预测市场动向的重要工具。布林带(Bollinger Bands)作为一种动态波动范围指标,因其直观性和实用性而广受欢迎。本文将通过Python代码,展示如何使用布林带结合K线图来分…...

现代密码学-认证、消息认证码
什么是单向散列函数 单向散列函数(one way hash function):一个输入:消息(message),一个固定长度的输出(散列值,hash value),根据散列值检查消息完整性(integrity) 单向散列函数也称为消息摘要…...

在Java中为什么对a赋值为10,在进行a++时还是等于10呢
首先我们看这样一组代码 public class demo1 {public static void main(String[] args) {int a10;aa;System.out.println(a);} } 结果:10不是在第二步有a操作吗?为什么还是10呢? a的执行步骤如下: 保存当前a的值(即10…...
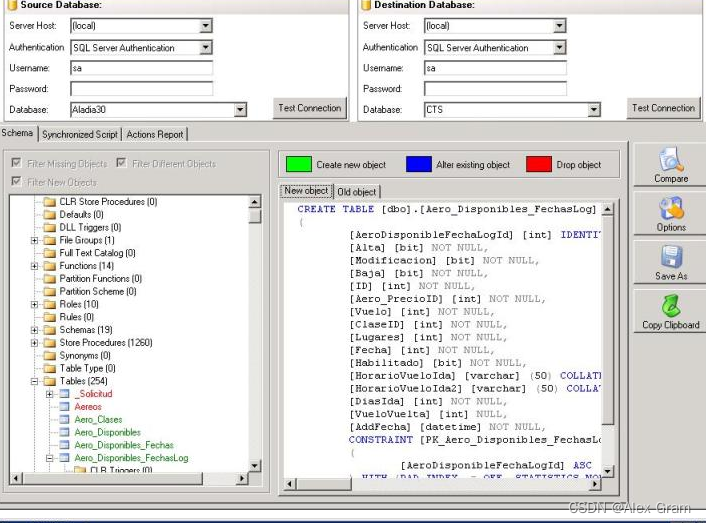
免费数据库同步软件
在信息化日益发展的今天,数据同步成为了企业和个人用户不可或缺的一部分。数据库同步软件作为数据同步的重要工具,能够帮助我们实现不同数据库系统之间的数据复制和同步,确保数据的一致性和完整性。本文将介绍几款免费数据库同步软件…...

如何轻松修改Windows远程连接的端口号
为了增强远程连接的安全性,最好修改默认的远程桌面协议(RDP)端口号。以下步骤将指导您如何修改Windows注册表中的端口设置,并相应地更新防火墙规则。 一、修改注册表中的端口号 打开注册表编辑器: 按下Win R键&#…...
)
Leetcode 54. 螺旋矩阵(二维数组移动坐标)
54. 螺旋矩阵 使用vis数组记录该位置是否已经被访问 定义一个int型dir来记录方向,0123分别代表右下左上 当越界或碰壁已访问的位置后,修改dir并计算下一个位置 否则根据原dir计算下一个位置 class Solution {public List<Integer> spiralOrder(i…...

深度图的方法实现加雾,Synscapes数据集以及D455相机拍摄为例
前言 在次之前,我们已经做了图像加雾的一些研究,这里我们将从深度图的方法实现加雾展开细讲 图像加雾算法的研究与应用_图像加雾 算法-CSDN博客 接下来将要介绍如何使用深度图像生成雾效图像的方法。利用Synscapes数据集,通过读取EXR格式的…...

QT: 读写ini配置文件(实现qml界面登录,修改)
目录 一.功能介绍 二.暴露属性 三.指定INI文件的路径和格式。 四.登录操作 1.检查INI文件中是否含有登录信息; 2.读取存储的ID; 3.读取存储的密码; 4.成功返回1;失败返回2; 五.修改账号 1.检查INI文件中是否含有登录信…...

DevOps 安全集成:从开发到部署,全生命周期安全守护
目录 一、DevOps 安全集成:为什么要做? 二、DevOps 安全集成:如何做? 三、DevOps 安全集成的优势 四、DevOps 安全集成:一些最佳实践 五、DevOps 安全集成:未来展望 六、思考与建议 七、总结 DevOps…...

R语言数据分析15-xgboost模型预测
XGBoost模型预测的主要大致思路: 1. 数据准备 首先,需要准备数据。这包括数据的读取、预处理和分割。数据应该包括特征和目标变量。 步骤: 读取数据:从CSV文件或其他数据源读取数据。数据清理:处理缺失值、异常值等…...
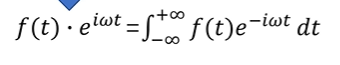
重构大学数学基础_week04_从点积理解傅里叶变换
这周我们来看一下傅里叶变换。傅里叶变换是一种在数学和许多科学领域中广泛应用的分析方法,它允许我们将信号或函数从其原始域(通常是时间域或空间域)转换到频域表示。在频域中,信号被表示为其组成频率的幅度和相位,这…...

Shell以及Shell编程
Shell的任务 ①分析命令; ②处理通配符、变量替换、命令替换、重定向、管道和作业控制; ③搜索命令并执行。 内部命令:内嵌在Shell中。 外部命令:存在于磁盘上的独立可执行文件。 #!/bin/bash #! 称为一个幻数&…...

从记忆到想象:探索AI的智能未来
引言 人工智能(AI)在信息处理、数据分析和任务自动化等方面展现了强大的能力。然而,在人类独有的记忆和想象力领域,AI仍然有很长的路要走。加利福尼亚大学戴维斯分校的心理学和神经科学教授查兰兰加纳特(Charan Ranga…...
“安全生产月”专题报道:AI智能监控技术如何助力安全生产
今年6月是第23个全国“安全生产月”,6月16日为全国“安全宣传咨询日”。今年全国“安全生产月”活动主题为“人人讲安全、个个会应急——畅通生命通道”。近日,国务院安委会办公室、应急管理部对开展好2024年全国“安全生产月”活动作出安排部署。 随着科…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
