AI绘画中的图像格式技术
在数字艺术的广阔天地里,AI绘画作为一种新兴的艺术形式,正在逐渐占据一席之地。不同于传统绘画,AI绘画依赖于复杂的算法和机器学习模型来生成图像,而这一切的背后,图像格式技术发挥着至关重要的作用。图像格式不仅关系到艺术作品的质量和表现力,还影响着创作过程的效率和可行性。
在探讨图像格式对AI绘画的影响时,首先得认识到不同的图像格式具有不同的特性,如无损压缩与有损压缩、支持的色彩深度、透明度、分辨率等。这些特性决定了图像的最终展现形式,进而影响AI绘画的输出效果。
无损压缩格式,如PNG,保留了图像的所有细节信息。这对于AI绘画来说极为重要,因为像素级别的细微变化都可能代表着艺术家的创作意图。然而,无损格式通常文件较大,对算力和存储提出了更高的要求。相对而言,有损压缩格式如JPEG,通过舍弃部分图像信息来减少文件大小,但可能导致细节丢失,对于精细的AI绘画来说,这可能不是最佳选择。
色彩深度是另一个重要因素。例如,8位的图像只能显示256种颜色,而32位图像则能够展示上百万种颜色。显然,更高的色彩深度能够提供更丰富的颜色渐变和更细腻的纹理效果,增强AI绘画的视觉冲击力和艺术表现力。
透明度的支持也是不可或缺的一环,特别是对于那些需要合成到不同背景中的AI绘画作品。带有alpha通道的图像格式,如TGA或PNG,允许艺术家创作出边缘柔和、能够无缝融入各种环境的作品。
高分辨率图像格式为AI绘画提供了更多的画布空间,使得作品能够展现出更多细节。随着分辨率的提升,计算资源的需求也随之增长。因此,在选择图像格式时,艺术家和开发者必须在视觉效果和性能之间找到平衡点。
图像格式技术对AI绘画产生深远影响的一个实例便是神经网络的训练与应用。训练一个用于生成艺术的神经网络时,输入图像的质量直接决定了网络学习的效率和结果的品质。高质量的图像格式能够更好地保留训练数据中的特征,从而加速训练过程,并提高生成图像的精确度。
在实际应用中,采用合适的图像格式可以极大地提升AI绘画的交互体验。当艺术家在软件中实时预览AI生成的画作时,优化过的图像加载和渲染速度能够减少延迟,使得创作过程更加流畅。
展望未来,图像格式技术的发展将继续推动AI绘画的革新。随着新一代图像格式的出现,我们预计会有更高压缩效率、更广色域覆盖以及更佳性能的特点,这将进一步提升AI绘画的质感与创作的可能性。
赠送!
帮你去除照片上多余的衣物,四端整合版ai工具
https://pan.baidu.com/s/1dAIImpIqDDAumzyBBPoZOA?pwd=9999
提取码:9999
解压密码:ai_gongju
AI绘画的世界是无限广阔的,而图像格式技术正是那把钥匙,解锁着艺术创作的新领域。作为艺术与技术的交汇点,AI绘画不断挑战和重新定义我们对艺术的认知。图像格式技术的进步,无疑将加深人机合作的创作深度,赋予艺术更多的自由和灵魂。在数字的浪潮中,让我们期待AI绘画带来的下一场视觉盛宴。
相关文章:

AI绘画中的图像格式技术
在数字艺术的广阔天地里,AI绘画作为一种新兴的艺术形式,正在逐渐占据一席之地。不同于传统绘画,AI绘画依赖于复杂的算法和机器学习模型来生成图像,而这一切的背后,图像格式技术发挥着至关重要的作用。图像格式不仅关系…...

前端如何封装自己的npm包并且发布到npm注册源
前言 在前端开发中,复用代码是一种常见且高效的实践。通过封装和发布自己的npm包,你可以轻松地在多个项目之间共享代码,并且贡献给社区。以下是一步一步指导你如何封装自己的npm包并发布到npm注册源。 步骤一:创建并设置项目 首…...

vue油色谱画 大卫三角形|大卫五边形|PD图
大卫三角形 大卫五边形 PD图...

【React】前端插件 uuidjs 的使用 --随机生成id
文档1 文档2 使用 1.安装 npm install uuid2.Create a UUID import { v4 as uuidv4 } from uuid; uuidv4(); // ⇨ 9b1deb4d-3b7d-4bad-9bdd-2b0d7b3dcb6d3.或使用 CommonJS语法 const { v4: uuidv4 } require(uuid); uuidv4(); // ⇨ 1b9d6bcd-bbfd-4b2d-9b5d-ab8dfbbd4…...
ctfshow-web入门-信息搜集(web11-web20)
目录 1、web11 2、web12 3、web13 4、web14 5、web15 6、web16 7、web17 8、web18 9、web19 10、web20 1、web11 域名其实也可以隐藏信息,比如flag.ctfshow.com 就隐藏了一条信息 查询域名的 DNS 记录,类型为 TXT(域名的说明&#…...
C语言详解(动态内存管理)2
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...
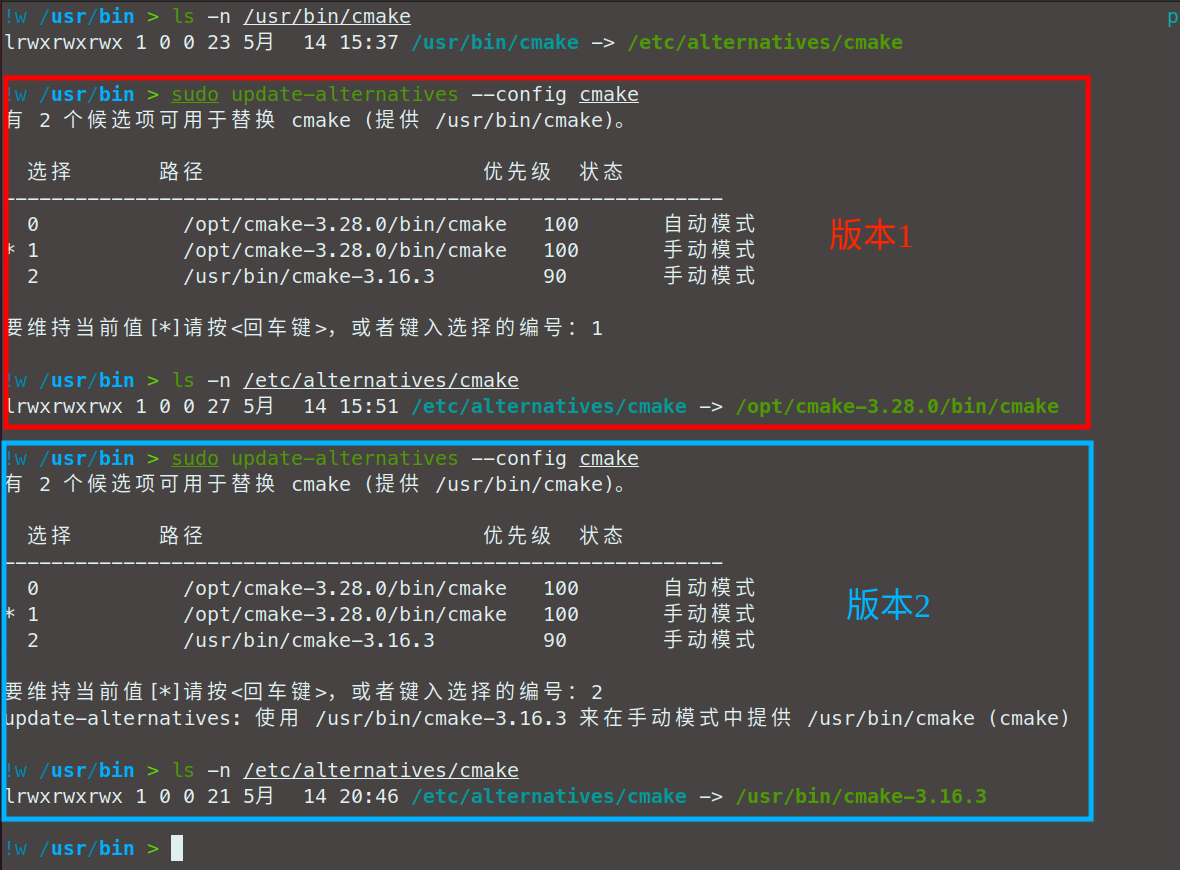
【ubuntu软件版本管理】利用update-alternatives管理ubuntu软件
我们有的时候希望在安装了新软件之后保留旧版本的软件,比如希望保留旧版本的gcc,以防以前写的C编译出问题,这时候就需要版本管理软件update-alternatives。 在此之前我们需要先弄清楚,什么是ubuntu的软件?拿C源…...

如何把linux安装到单片机中
1.如何把linux安装到单片机中 将Linux安装到单片机中通常不是一个直接的过程,因为单片机(如51系列、STC系列等)的硬件资源和处理能力有限,而Linux是一个为更强大硬件平台(如个人电脑、服务器)设计的操作系…...

Ubuntu bash按Table不联想
Ubuntu bash按Table不联想 bash-completion包未安装或损坏: 自动补全功能依赖于bash-completion包。首先,需要确保这个包已经安装。可以通过下面的命令安装或重新安装它: sudo apt install --reinstall bash-completion安装完成后,…...
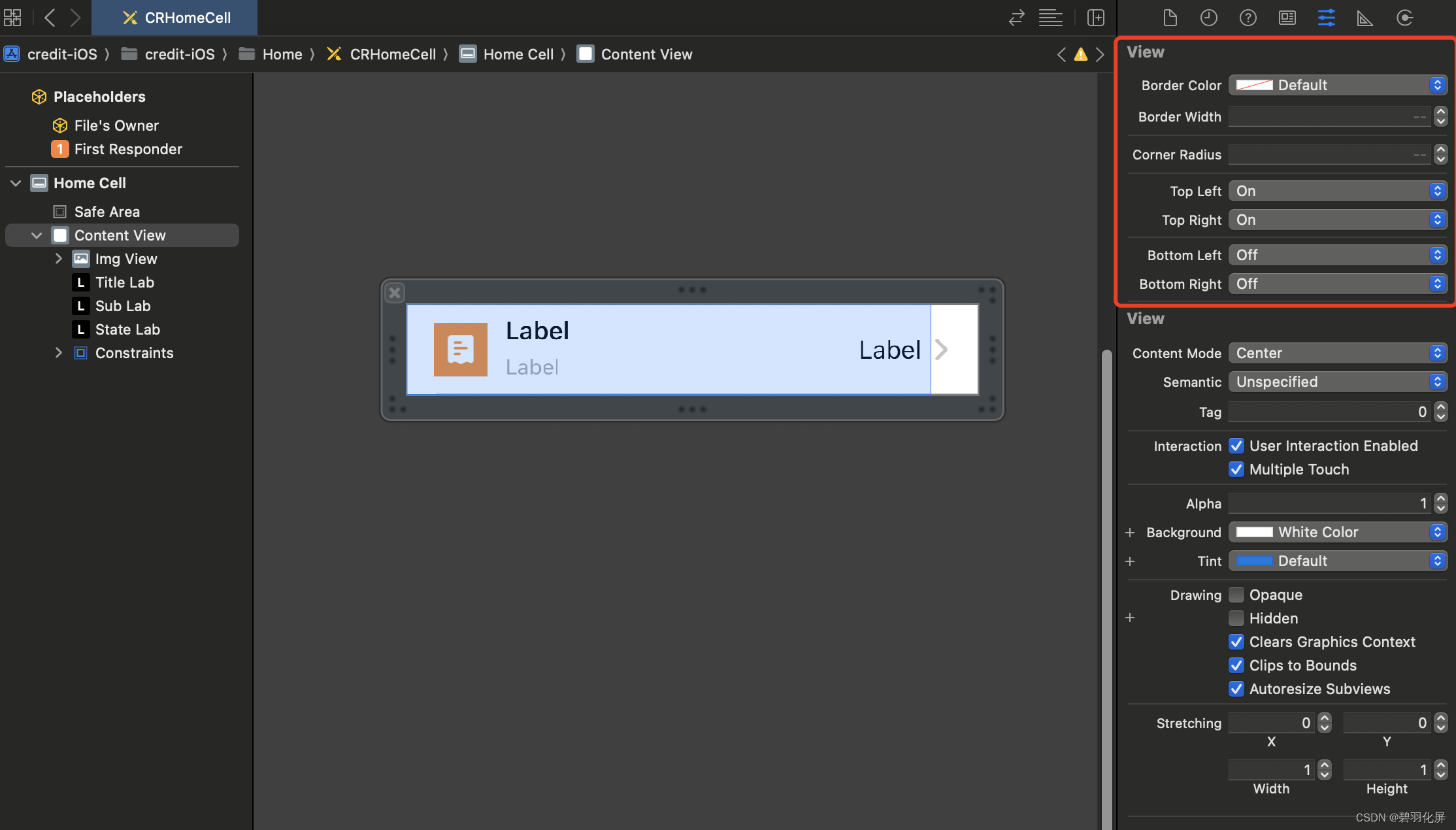
Xcode中给UIView在xib中添加可视化的属性
给UIView在xib中添加可视化的属性 效果如下图: 可以直接设置view 的 borderColor 、borderWidth、cornerRadius,也可以单独指定view的某个角是圆角。减少了代码中的属性。 完整代码: UIViewBorder.h #import <UIKit/UIKit.h>inter…...

中缀表达式和前缀后缀
在中缀表达式中,操作数可能与两个操作符相结合 但是,想要不带括号无歧义,且不需要考虑运算符优先级和结合性 所以考虑 前缀表达式,波兰表达式 后缀表达式 逆波兰表达式 对于人来说,中缀表达式是最容易读懂的。但是对于…...

强化学习面试题
强化学习面试题通常会涵盖该领域的多个方面,包括基本概念、算法、应用以及实践问题。以下是一些常见的强化学习面试题及其简要回答: 基本概念题: 什么是强化学习? 强化学习是一种通过智能体与环境交互来学习最优行为策略的机器学习范式。智能体根据当前状态选择动作,环境…...

Pytorch中的广播机制
一、广播(broadcast)机制概述 在PyTorch中,广播机制(Broadcast)允许对不同形状的张量执行逐元素操作,而无需显式地复制数据。这一机制使得编写代码更加简洁和高效。广播机制遵循一定的规则来扩展较小的张量,使其与较大的张量具有相同的形状 …...

2024年全国一高考数学压轴题
(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n 2 } \{a_{1},...,a_{4n2}\} {a1,...,a4n2} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n 2 } \{1,...,4n2\} {1,...,4n2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去…...

springboot+vue前后端项目接口校验通信数据完整性
方案:使用国密SM3算法实现数字签名 服务端 maven的pom文件引用 <!-- 国密算法支持 --><dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15to18</artifactId><version>1.69</version><…...

进程通信(IPC-Inter Process Communication)
进程之间的通信通过内核空间实现 IPC技术 ①管道(匿名管道/命名管道-FIFO队列) ②System V IPC(消息队列、信号量和共享内存) ③套接字(UNIX套接字&Internet套接字) ※信号 软中断,信号提供了一种处理异步事件的方法,作为进程通信的一种机制&am…...
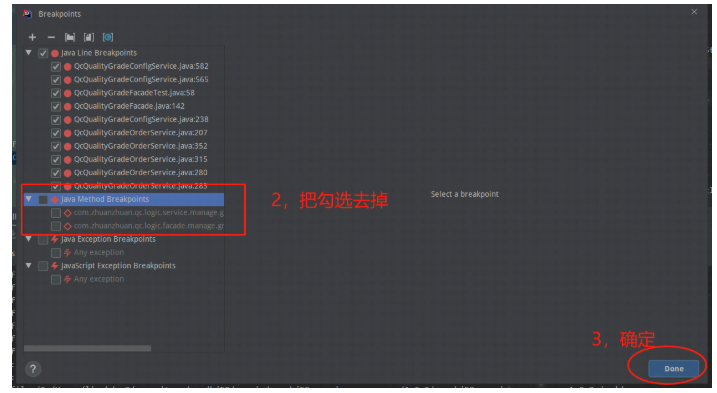
idea debug时提示”Method breakpoints may dramatically slow down debugging“的解决办法
问题现象 今天同事喊我过去看一个问题,项目正常启动的时候没问题,debug模式就卡住了,很久不动。我推测是哪个断点导致的,一看断点果然有情况。在方法上打了断点。 解决方式(Android Studio一样的解决) 1、View Brea…...
计算机缺失msvcp100.dll如何解决?教你5种简单高效的修复方法
在现代科技发展的时代,计算机已经成为我们生活和工作中不可或缺的工具。然而,在使用计算机的过程中,我们常常会遇到各种问题和困扰。其中之一就是计算机找不到msvcp100.dll文件。这个问题可能会给我们的生活和工作带来很多不便,下…...

对硬盘的设想2:纸存,硬指针,软指针
“纸存”是设想中的存储器,它只能改写两次:写一次,再改一次,然后就不能再动了。就像拿着钢笔在纸上写字一样,所以叫纸存。 硬指针P、软指针S S abcd S aPcdPx P aPcdPx S aycd ①一个软指针S,指向数据abcd…...

Python在股票交易分析中的应用:布林带与K线图的实战回测
引言 在股票交易的世界中,技术分析是投资者们用来预测市场动向的重要工具。布林带(Bollinger Bands)作为一种动态波动范围指标,因其直观性和实用性而广受欢迎。本文将通过Python代码,展示如何使用布林带结合K线图来分…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
