当前位置： 首页 > news >正文

中缀表达式和前缀后缀

news 2026/2/1 13:22:49

在这里插入图片描述
在中缀表达式中，操作数可能与两个操作符相结合
但是，想要不带括号无歧义，且不需要考虑运算符优先级和结合性
所以考虑
前缀表达式，波兰表达式
后缀表达式 逆波兰表达式
对于人来说，中缀表达式是最容易读懂的。但是对于机器来说，想要省略掉括号那部分内存，就要用前缀表达式和后缀表达式
从编程的角度来讲，后缀表达式最容易解析，求值的时间和内存的代价最小

在这里插入图片描述

后缀表达式的求值

从左往右
遇到操作数则压栈，遇到操作符弹出两个操作数并将结果压入栈
最后取栈顶作为结果

前缀表达式

从右往左
遇到操作数则压栈，遇到操作符弹出两个操作数并将结果压入栈
最后取栈顶作为结果

相关文章：

中缀表达式和前缀后缀

在中缀表达式中，操作数可能与两个操作符相结合 但是，想要不带括号无歧义，且不需要考虑运算符优先级和结合性 所以考虑 前缀表达式，波兰表达式 后缀表达式 逆波兰表达式 对于人来说，中缀表达式是最容易读懂的。但是对于…...

编程日记 2024/6/8 23:22:11

强化学习面试题

强化学习面试题通常会涵盖该领域的多个方面，包括基本概念、算法、应用以及实践问题。以下是一些常见的强化学习面试题及其简要回答： 基本概念题： 什么是强化学习？ 强化学习是一种通过智能体与环境交互来学习最优行为策略的机器学习范式。智能体根据当前状态选择动作，环境…...

编程日记 2024/6/8 23:21:10

Pytorch中的广播机制

一、广播(broadcast)机制概述 在PyTorch中，广播机制(Broadcast)允许对不同形状的张量执行逐元素操作，而无需显式地复制数据。这一机制使得编写代码更加简洁和高效。广播机制遵循一定的规则来扩展较小的张量，使其与较大的张量具有相同的形状 …...

编程日记 2024/6/8 23:20:09

2024年全国一高考数学压轴题

(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n 2 } \{a_{1},...,a_{4n2}\} {a1​,...,a4n2​} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n 2 } \{1,...,4n2\} {1,...,4n2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去…...

编程日记 2024/6/8 23:17:07

springboot+vue前后端项目接口校验通信数据完整性

方案&#xff1a;使用国密SM3算法实现数字签名 服务端 maven的pom文件引用 <!-- 国密算法支持 --><dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15to18</artifactId><version>1.69</version><…...

编程日记 2024/6/8 23:16:06

进程通信(IPC-Inter Process Communication)

进程之间的通信通过内核空间实现 IPC技术 ①管道(匿名管道/命名管道-FIFO队列) ②System V IPC(消息队列、信号量和共享内存) ③套接字(UNIX套接字&Internet套接字) ※信号 软中断&#xff0c;信号提供了一种处理异步事件的方法&#xff0c;作为进程通信的一种机制&am…...

编程日记 2024/6/8 23:15:05

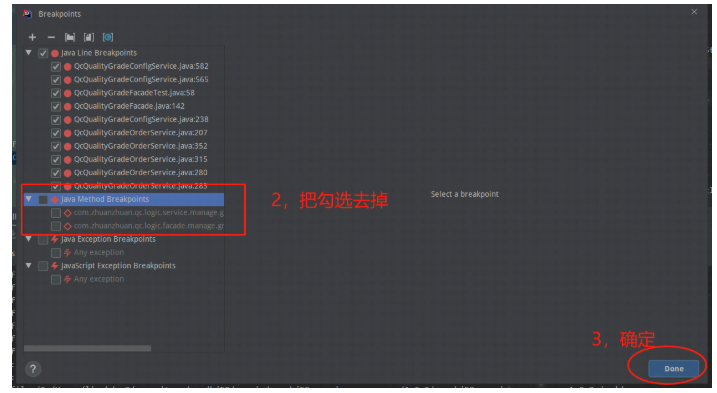
idea debug时提示”Method breakpoints may dramatically slow down debugging“的解决办法

问题现象 今天同事喊我过去看一个问题&#xff0c;项目正常启动的时候没问题&#xff0c;debug模式就卡住了&#xff0c;很久不动。我推测是哪个断点导致的&#xff0c;一看断点果然有情况。在方法上打了断点。 解决方式(Android Studio一样的解决&#xff09; 1、View Brea…...

编程日记 2024/6/8 23:13:02

计算机缺失msvcp100.dll如何解决？教你5种简单高效的修复方法

在现代科技发展的时代&#xff0c;计算机已经成为我们生活和工作中不可或缺的工具。然而&#xff0c;在使用计算机的过程中&#xff0c;我们常常会遇到各种问题和困扰。其中之一就是计算机找不到msvcp100.dll文件。这个问题可能会给我们的生活和工作带来很多不便&#xff0c;下…...

编程日记 2024/6/8 23:12:01

对硬盘的设想2：纸存，硬指针，软指针

“纸存”是设想中的存储器&#xff0c;它只能改写两次&#xff1a;写一次&#xff0c;再改一次&#xff0c;然后就不能再动了。就像拿着钢笔在纸上写字一样&#xff0c;所以叫纸存。 硬指针P、软指针S S abcd S aPcdPx P aPcdPx S aycd ①一个软指针S&#xff0c;指向数据abcd…...

编程日记 2024/6/8 23:11:00

Python在股票交易分析中的应用：布林带与K线图的实战回测

引言 在股票交易的世界中&#xff0c;技术分析是投资者们用来预测市场动向的重要工具。布林带&#xff08;Bollinger Bands&#xff09;作为一种动态波动范围指标&#xff0c;因其直观性和实用性而广受欢迎。本文将通过Python代码&#xff0c;展示如何使用布林带结合K线图来分…...

编程日记 2024/6/8 23:08:58

现代密码学-认证、消息认证码

什么是单向散列函数 单向散列函数&#xff08;one way hash function&#xff09;&#xff1a;一个输入&#xff1a;消息&#xff08;message&#xff09;,一个固定长度的输出(散列值&#xff0c;hash value),根据散列值检查消息完整性(integrity) 单向散列函数也称为消息摘要…...

编程日记 2024/6/8 23:07:58

在Java中为什么对a赋值为10，在进行a++时还是等于10呢

首先我们看这样一组代码 public class demo1 {public static void main(String[] args) {int a10;aa;System.out.println(a);} } 结果&#xff1a;10不是在第二步有a操作吗&#xff1f;为什么还是10呢&#xff1f; a的执行步骤如下&#xff1a; 保存当前a的值&#xff08;即10…...

编程日记 2024/6/8 23:06:57

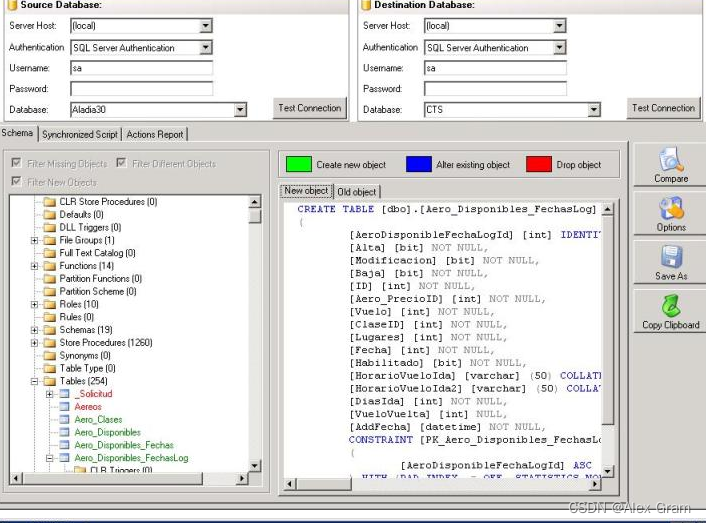
免费数据库同步软件

在信息化日益发展的今天&#xff0c;数据同步成为了企业和个人用户不可或缺的一部分。数据库同步软件作为数据同步的重要工具&#xff0c;能够帮助我们实现不同数据库系统之间的数据复制和同步&#xff0c;确保数据的一致性和完整性。本文将介绍几款免费数据库同步软件&#xf…...

编程日记 2024/6/8 23:05:56

如何轻松修改Windows远程连接的端口号

为了增强远程连接的安全性&#xff0c;最好修改默认的远程桌面协议&#xff08;RDP&#xff09;端口号。以下步骤将指导您如何修改Windows注册表中的端口设置&#xff0c;并相应地更新防火墙规则。 一、修改注册表中的端口号 打开注册表编辑器&#xff1a; 按下Win R键&#…...

编程日记 2024/6/8 23:04:55

Leetcode 54. 螺旋矩阵（二维数组移动坐标）

54. 螺旋矩阵 使用vis数组记录该位置是否已经被访问 定义一个int型dir来记录方向&#xff0c;0123分别代表右下左上 当越界或碰壁已访问的位置后&#xff0c;修改dir并计算下一个位置 否则根据原dir计算下一个位置 class Solution {public List<Integer> spiralOrder(i…...

编程日记 2024/6/8 23:03:54

深度图的方法实现加雾，Synscapes数据集以及D455相机拍摄为例

前言 在次之前&#xff0c;我们已经做了图像加雾的一些研究&#xff0c;这里我们将从深度图的方法实现加雾展开细讲 图像加雾算法的研究与应用_图像加雾 算法-CSDN博客 接下来将要介绍如何使用深度图像生成雾效图像的方法。利用Synscapes数据集&#xff0c;通过读取EXR格式的…...

编程日记 2024/6/8 23:01:52

QT: 读写ini配置文件(实现qml界面登录，修改)

目录 一.功能介绍 二.暴露属性 三.指定INI文件的路径和格式。 四.登录操作 1.检查INI文件中是否含有登录信息&#xff1b; 2.读取存储的ID&#xff1b; 3.读取存储的密码; 4.成功返回1&#xff1b;失败返回2&#xff1b; 五.修改账号 1.检查INI文件中是否含有登录信…...

编程日记 2024/6/8 23:00:51

DevOps 安全集成：从开发到部署，全生命周期安全守护

目录 一、DevOps 安全集成&#xff1a;为什么要做&#xff1f; 二、DevOps 安全集成&#xff1a;如何做&#xff1f; 三、DevOps 安全集成的优势 四、DevOps 安全集成&#xff1a;一些最佳实践 五、DevOps 安全集成&#xff1a;未来展望 六、思考与建议 七、总结 DevOps…...

编程日记 2024/6/8 22:58:48

R语言数据分析15-xgboost模型预测

XGBoost模型预测的主要大致思路&#xff1a; 1. 数据准备 首先&#xff0c;需要准备数据。这包括数据的读取、预处理和分割。数据应该包括特征和目标变量。 步骤&#xff1a; 读取数据&#xff1a;从CSV文件或其他数据源读取数据。数据清理&#xff1a;处理缺失值、异常值等…...

编程日记 2024/6/8 22:56:47

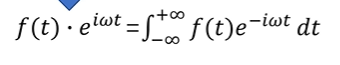
重构大学数学基础_week04_从点积理解傅里叶变换

这周我们来看一下傅里叶变换。傅里叶变换是一种在数学和许多科学领域中广泛应用的分析方法&#xff0c;它允许我们将信号或函数从其原始域&#xff08;通常是时间域或空间域&#xff09;转换到频域表示。在频域中&#xff0c;信号被表示为其组成频率的幅度和相位&#xff0c;这…...

编程日记 2024/6/8 22:55:46

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

概述 在 Swift 开发语言中&#xff0c;各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过&#xff0c;在涉及到多个子类派生于基类进行多态模拟的场景下&#xff0c;…...

编程新知 2026/1/23 4:56:05

uniapp微信小程序视频实时流+pc端预览方案

方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度​WebSocket图片帧​定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐​RTMP推流​TRTC/即构SDK推流❌ 付费方案 &#xff08;部分有免费额度&#x…...

编程新知 2026/1/31 6:12:33

今日科技热点速览

&#x1f525; 今日科技热点速览 &#x1f3ae; 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售&#xff0c;主打更强图形性能与沉浸式体验&#xff0c;支持多模态交互&#xff0c;受到全球玩家热捧 。 &#x1f916; 人工智能持续突破 DeepSeek-R1&…...

编程新知 2025/11/20 14:26:29

AGain DB和倍数增益的关系

我在设置一款索尼CMOS芯片时&#xff0c;Again增益0db变化为6DB&#xff0c;画面的变化只有2倍DN的增益&#xff0c;比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析&#xff1a; 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

编程新知 2025/9/30 16:23:57

规则与人性的天平——由高考迟到事件引发的思考

当那位身着校服的考生在考场关闭1分钟后狂奔而至&#xff0c;他涨红的脸上写满绝望。铁门内秒针划过的弧度&#xff0c;成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定"&#xff0c;构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

编程新知 2026/1/15 17:33:18

一些实用的chrome扩展0x01

简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序&#xff0c;无论是测试应用程序、搜寻漏洞还是收集情报&#xff0c;它们都能提升工作流程。 FoxyProxy 代理管理工具&#xff0c;此扩展简化了使用代理&#xff08;如 Burp…...

编程新知 2026/1/25 15:45:49

Mysql故障排插与环境优化

前置知识点 最上层是一些客户端和连接服务&#xff0c;包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念&#xff0c;为通过安全认证接入的客户端提供线程。同样在该层上可…...

编程新知 2026/1/31 8:42:40

Axure零基础跟我学：展开与收回

亲爱的小伙伴，如有帮助请订阅专栏！跟着老师每课一练，系统学习Axure交互设计课程！ Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题：Axure菜单展开与收回 课程视频：...

编程新知 2026/1/26 19:46:33

篇章一 论坛系统——前置知识

目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构​编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...

编程新知 2026/1/27 0:55:08

AI书签管理工具开发全记录（十八）：书签导入导出

文章目录 AI书签管理工具开发全记录&#xff08;十八&#xff09;&#xff1a;书签导入导出1.前言 &#x1f4dd;2.书签结构分析 &#x1f4d6;3.书签示例 &#x1f4d1;4.书签文件结构定义描述 &#x1f523;4.1. ​整体文档结构​​4.2. ​核心元素类型​​4.3. ​层级关系4.…...

编程新知 2026/1/29 21:17:14