最小相位系统
最小相位系统
1、传递函数
一个线性系统的响应。
比如一个RC低通滤波器:
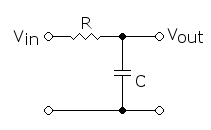
交流分量在电容的充放电中被滤除掉,通过设置电容器的电容值,以及电阻值,能够控制这种滤除能力,这个参数为RC。
电容的电抗为 1 / j w C 1/jwC 1/jwC,因此容易的写出其频率响应,其中 V i n = ∑ k = 1 L A k ℜ { exp ( j ϕ k ) exp ( j w t ) } V_{in} = \sum_{k=1}^{L}A_k\Re\{\exp(j\phi_k)\exp(jwt)\} Vin=∑k=1LAkℜ{exp(jϕk)exp(jwt)}:
V o u t = 1 / j w C R + 1 / j w C V i n = 1 1 + j w R C V i n V_{out} = \frac{1/jwC}{R+1/jwC} V_{in} = \frac{1}{1+jwRC} V_{in} Vout=R+1/jwC1/jwCVin=1+jwRC1Vin
将这个系数提出来:
H ( w ) = 1 1 + j w R C H(w) = \frac{1}{1+jwRC} H(w)=1+jwRC1
这是一个变量为角频率的复变函数。为了便于在二维空间展示,对其取模、取相角,分别得到幅频响应和相频响应。求逆傅立叶变换得到 h ( t ) h(t) h(t),冲激函数响应。
此时的 H ( w ) H(w) H(w)是一种传递函数(transfer function)。
以上是简单情况,仅当输入信号存在傅立叶变换的时候才成立,傅立叶变换要求输入信号绝对可积。对于更一般的情况,对频率进行推广。傅立叶变换的核函数是 e j w t e^{jwt} ejwt,将纯虚数推广到复数,就能够对幅度进行调控,即 e s t = e ( a + j b ) t = e a t e j b t e^{st}=e^{(a+jb)t}=e^{at}e^{jbt} est=e(a+jb)t=eatejbt。至于衰减还是增加,取决于 a a a的正负。
得到:
H ( s ) = 1 1 + s R C H(s) = \frac{1}{1+sRC} H(s)=1+sRC1
当s取纯虚数的时候,等于频率响应。
为了便于分析,将 H ( s ) H(s) H(s)画在一个复平面上,横轴为实轴,纵轴为虚轴。
这个系统是一个因果系统,没有输入的时候不会有输出。因此其时域响应是一个右边信号,因此其收敛域为 R O C = { s ∣ ∣ s ∣ > − R C } ROC = \{s\mid |s|> -RC\} ROC={s∣∣s∣>−RC}。
包含虚轴,那么该系统稳定。有理+极点在左半平面,因此系统因果。
2、最小相位
比较相位大小,首先要保证幅频响应相同,或者说幅度增益相同,否则没有意义。
结论:系统首先要求因果+稳定
- 拉普拉斯变换:零极点都在左半复平面
- z变换:零极点都在单位圆内
则是最小相位系统
首先系统要求稳定,即有界输入对应有界输出,其充要条件是ROC包含虚轴。
其次系统要求因果,即 h ( t ) = 0 , ∀ t < 0 h(t)=0,\forall t<0 h(t)=0,∀t<0,暂时没有好的充要条件,但又一些有意义的结论:
- 必要条件:ROC是某个右半复平面。( h ( t ) h(t) h(t)至少要求是右边信号,起点还不确定,所以仅仅是个必要条件)
- 充分条件:传递函数是有理的,并且ROC为最右侧极点的右半复平面。
那么,下面的讨论中,假设传递函数可以用有理函数表示。(这意味着其时域响应可以用复指数函数表示)
H ( s ) = N ( s ) D ( s ) (2-1) H(s) = \frac{N(s)}{D(s)} \tag{2-1} H(s)=D(s)N(s)(2-1)
接下来再说什么情况下两个系统的幅度增益是相同的。
∣ H 1 ( s ) ∣ = ∣ N 1 ( s ) ∣ ∣ D 1 ( s ) ∣ = ∣ N 2 ( s ) ∣ ∣ D 2 ( s ) ∣ = ∣ H 2 ( s ) ∣ (2-2) |H_1(s)| = \frac{|N_1(s)|}{|D_1(s)|} =\frac{|N_2(s)|}{|D_2(s)|} =|H_2(s)| \tag{2-2} ∣H1(s)∣=∣D1(s)∣∣N1(s)∣=∣D2(s)∣∣N2(s)∣=∣H2(s)∣(2-2)
从上面公式(2-2)可以看出,幅度相同,意味着分子分母的幅度都相同。
根据有理传递函数的假设,其分子分母都可以用多项式表示,再由代数基本定理,该多项式可以写成连乘的形式。
先讨论分母,其中A是一个常数, a i , i = 1 , 2 , . . . , N a_i,i=1,2,...,N ai,i=1,2,...,N:
D ( s ) = A Π i = 1 N ( 1 − a i s − 1 ) = A ( 1 − a 1 s − 1 ) ( 1 − a 2 s − 1 ) ⋯ ( 1 − a N s − 1 ) (2-3) D(s) = A\Pi_{i=1}^N(1-a_is^{-1}) = A(1-a_1s^{-1})(1-a_2s^{-1})\cdots(1-a_Ns^{-1}) \tag{2-3} D(s)=AΠi=1N(1−ais−1)=A(1−a1s−1)(1−a2s−1)⋯(1−aNs−1)(2-3)
如果要求系统因果稳定,那么 ℜ { a i } < 0 \Re\{a_i\}<0 ℜ{ai}<0,且ROC为右半平面。
因此必有 D 1 ( s ) = D 2 ( s ) D_1(s)=D_2(s) D1(s)=D2(s),否则必有一个不满足因果稳定的条件。
再讨论分子,其中B是一个常数, b i , i = 1 , 2 , . . . , M b_i,i=1,2,...,M bi,i=1,2,...,M:
N ( s ) = B Π i = 1 M ( 1 − b i s − i ) = B ( 1 − b 1 s − 1 ) ( 1 − b 2 s − 1 ) ⋯ ( 1 − b M s − 1 ) (2-4) N(s) = B\Pi_{i=1}^M(1-b_is^{-i}) = B(1-b_1s^{-1})(1-b_2s^{-1})\cdots(1-b_Ms^{-1}) \tag{2-4} N(s)=BΠi=1M(1−bis−i)=B(1−b1s−1)(1−b2s−1)⋯(1−bMs−1)(2-4)
系统因果稳定跟分子没有关系,因此 b i ∈ C b_i\in C bi∈C,为任意复数。
因此,两个因果稳定的系统,幅度增益相同,相位响应不同,只能从分子入手,分母不能动。
对任意一项 ( 1 − b i s − 1 ) (1-b_is^{-1}) (1−bis−1),其中 s = σ + j w , b i = x + j y s=\sigma+jw,b_i = x+jy s=σ+jw,bi=x+jy。取相角:
ϕ = ∡ ( 1 − b i s − 1 ) = arg ( 1 − x + j y σ + j w ) = arg ( σ − x + j ( w − y ) σ + j w ) = arg ( K e ϕ 1 − ϕ 2 ) K = ( σ − x ) 2 + ( w − y ) 2 σ 2 + w 2 ϕ = ϕ 1 − ϕ 2 = arctan 2 ( w − y σ − x ) − arctan ( w σ ) \phi = \measuredangle (1-b_is^{-1})= \arg (1-\frac{x+jy}{\sigma+jw}) =\arg(\frac{\sigma-x+j(w-y)}{\sigma+jw}) = \arg(Ke^{\phi_1-\phi_2}) \\ K = \frac{\sqrt{(\sigma-x)^2+(w-y)^2}}{\sqrt{\sigma^2+w^2}}\\ \phi = \phi_1-\phi_2 = \arctan2(\frac{w-y}{\sigma-x}) - \arctan(\frac{w}{\sigma}) ϕ=∡(1−bis−1)=arg(1−σ+jwx+jy)=arg(σ+jwσ−x+j(w−y))=arg(Keϕ1−ϕ2)K=σ2+w2(σ−x)2+(w−y)2ϕ=ϕ1−ϕ2=arctan2(σ−xw−y)−arctan(σw)
讨论相频响应,需要令 σ = 0 \sigma=0 σ=0,频率 w w w从0开始递增,通常使用波特图来描述,横坐标用类似于np.linspace(1e-2,1e2,1000)的语句来描述。
因此 ϕ 2 = π / 2 \phi_2=\pi/2 ϕ2=π/2, ϕ 1 = arctan 2 ( w − y − x ) \phi_1 = \arctan2(\frac{w-y}{-x}) ϕ1=arctan2(−xw−y),需要注意 arctan 2 \arctan2 arctan2的输出范围是 [ − π , π ) [-\pi,\pi) [−π,π)。因此当 − x > 0 -x>0 −x>0为常数, w − y > 0 w-y>0 w−y>0的时候,返回的是一个一象限的锐角,因此 ϕ 1 \phi_1 ϕ1从 − π / 2 -\pi/2 −π/2递增到0。反过来将从 π / 2 \pi/2 π/2递减到0
可以用python代码来描述这个过程:
import numpy as np
import matplotlib.pylab as plt
# (1-bs^-1)
sigma = 0
Npoints = 1000
w = np.linspace(1e-1,100,Npoints)
s = sigma+1j*wb = -5+1j*0y1 = np.angle((1-b/s), deg=True)
y2 = np.angle((1+b.conjugate()/s), deg=True)x1 = np.abs(1-b/s)
x2 = np.abs(1+b.conjugate()/s)
plt.semilogx(w,y1,'ro')
plt.semilogx(w,y2,'b*')
plt.legend(["negtive poles","positive poles"])
plt.show()
上述推导属实令人费解,主要原因是我们采用了负幂来描述这个系统。实际上,在控制工程当中,使用正幂来描述连续时间系统会更加常见。
如果是正幂,那么分子中的一项为 ( s − b i ) (s-b_i) (s−bi),令s的实部为0,即 s = j w s=jw s=jw,那么
∡ ( s − b i ) = a r c t a n 2 ( w − y − x ) ∣ ( s − b i ) ∣ = x 2 + ( w − y ) 2 (2-5) \measuredangle(s-b_i) = arctan2(\frac{w-y}{-x}) \\ |(s-b_i)| = \sqrt{x^2+(w-y)^2} \tag{2-5} ∡(s−bi)=arctan2(−xw−y)∣(s−bi)∣=x2+(w−y)2(2-5)
显然,要使得幅频响应不变,那么 b i b_i bi的虚部不能动,实部的正负可以变。
| ( w − y ) > 0 (w-y)>0 (w−y)>0 | ( w − y ) < 0 (w-y)<0 (w−y)<0 | |
|---|---|---|
| 实部为正(位于正半平面) | 正钝角 | 负钝角 |
| 实部为负(位于负半平面) | 正锐角 | 负锐角 |
所以,当实部为负,即零点在负半平面,随着频率的变化,相位变化相比于零点在正半平面更慢。也就是说相位变化小,即群时延小,阶跃响应建立更快,冲激响应能量更向0时刻集中。需要注意,最小相位系统,其相位延迟不一定是最小,但是相位变化一定是最小。比如一个最小相位系统的相位延迟了45度,另外一个相同幅频响应的系统相位延迟可能只有30度。
总结
Tip1:
关于最小相位系统有一些等价条件:
- 群时延最小的系统
- 冲激响应能量最靠近0时刻的系统
- 阶跃响应建立最快的系统
- 有理传递函数的情况下,零极点都在复平面的左半平面的系统
- 有理传递函数的情况下,对于离散时间系统,零极点都在单位圆内的系统
- 有理传递函数的情况下,系统和逆系统都是因果稳定的系统
Tip2:
最大相位系统:零点都在右半平面。因此这种系统因果稳定,但是其逆系统则不可能同时因果稳定。
Tip3:
一个零极点系统可以表示成最小相位系统和全通系统的乘积。
比如:
H ( s ) = s − 1 ( s + 3 ) ( s + 2 ) = s − 1 ( s + 3 ) ( s + 2 ) × s − 1 s + 1 H(s) = \frac{s-1}{(s+3)(s+2)} = \frac{s-1}{(s+3)(s+2)}\times \frac{s-1}{s+1} H(s)=(s+3)(s+2)s−1=(s+3)(s+2)s−1×s+1s−1
H ( z ) = 1 − ( 2 e j π / 3 ) z − 1 ( 1 − 3 z − 1 ) ( 5 − z − 1 ) = z − 1 − 2 e − j π / 3 ( z − 1 − 3 ) ( 5 − z − 1 ) × 1 − ( 2 e j π / 3 ) z − 1 z − 1 − 2 e − j π / 3 × z − 1 − 3 1 − 3 z − 1 H(z) = \frac{1-(2e^{j\pi/3})z^{-1}}{(1-3z^{-1})(5-z^{-1})} = \frac{z^{-1} - 2e^{-j\pi/3}}{(z^{-1}-3)(5-z^{-1})} \times \frac{1-(2e^{j\pi/3})z^{-1}}{z^{-1} - 2e^{-j\pi/3}} \times \frac{z^{-1}-3}{1-3z^{-1}} H(z)=(1−3z−1)(5−z−1)1−(2ejπ/3)z−1=(z−1−3)(5−z−1)z−1−2e−jπ/3×z−1−2e−jπ/31−(2ejπ/3)z−1×1−3z−1z−1−3
Tip4:
已知幅频响应,那么其最小相位系统的相频响应响应是唯一的。
相关文章:

最小相位系统
最小相位系统 1、传递函数 一个线性系统的响应。 比如一个RC低通滤波器: 交流分量在电容的充放电中被滤除掉,通过设置电容器的电容值,以及电阻值,能够控制这种滤除能力,这个参数为RC。 电容的电抗为 1 / j w C 1/j…...

css系列:进度条
前言 技术来源于需求,近期遇到了做语音的需求,有个调整语速和音量的进度条,UI组件库的进度条大部分不支持拖动和点击修改当前进度,所以自己手写了一个。 实现思路 MDN文档介绍 <input type"range"> - HTML&am…...

QT中为程序加入超级管理员权限
QT中为程序加入超级管理员权限 Chapter1 QT中为程序加入超级管理员权限1. mingw编译器2. MSVC编译器3. CMAKE Chapter2 如何给QT程序添加管理员权限(UAC)的几种方法1、Qt Creator中方案一:(仅适用于使用msvc编译器)方案二:&#x…...
)
共识算法之争(PBFT,Raft,PoW,PoS,DPoS)
文章目录 共识算法拜占庭容错技术(Byzantine Fault Tolerance,BFT)PBFT:Practical Byzantine Fault Tolerance,实用拜占庭容错算法Raft协议POW(Proof of Work)工作量证明机制POSDPoS(Delegated Proof of St…...

抽象的java入门1.3.0
前言: 在1.2.0版本中我们介绍了public class hello {}并从中提取出两个新概 修饰符和作用域 public class hello {public static void main(String[] args) {System.out.println("Hello World");} } 正片: 这一期把剩余的内容刨析出来 pub…...

【Oracle生产运维】表空间可用性告警排查处理
1 前言 在生产环境中,一般设置表空间告警阈值是90%,在接到监控报警后,并不是需要立刻对表空间进行扩容。 决定是否扩容主要看表空间最近的增量是多少,假如剩余10%的空间还能支持1个月的增量,那就不需要急着扩容。如果…...

mac Network: use --host to expose
本地启动无法访问,这个不是权限问题是mac 主机端口安全策略,现在我们只需要开启端口自动检测就可以 npm run dev --host 网络:未暴露 方案一 1、执行 npm run dev -- --host 方案二 1、请在 vite.config.js server: {host: true } 1…...

ChatGPT-4o体验demo
OpenAI 最近推出了其最新的人工智能语言模型——GPT-4O。该模型是在原有 GPT-4 的基础上进行优化而成,旨在提升生成质量和响应速度。GPT-4O 采用了更加高效的架构设计,使其在处理复杂文本时表现出更快的速度和更高的准确性。GPT-4O 在训练过程中融入了最…...
FPGA SPI采集ADC7606数据
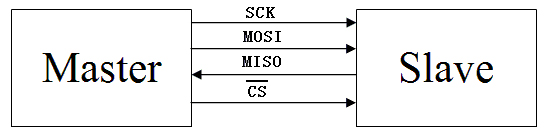
一,SPI总线的构成及信号类型 SPI总线只需四条线(如图1所示)就可以完成MCU与各种外围器件的通讯: 1)MOSI – Master数据输出,Slave数据输入 2)MISO – Master数据输入,Slave数据输出 3)SCK – 时钟信号,由Master产生 4)/CS – Slave使能信号,由Master控制。 在一个SPI时…...
html three.js 引入.stl模型示例
1.新建一个模块用于放置模型 <div id"chart_map" style"width:800px;height:500px"></div> 2. 引入代码根据需求更改 <!-- 在head或body标签内加入以下链接 --> <script src"https://cdn.jsdelivr.net/npm/three0.137/build/t…...

从零手写实现 nginx-11-文件处理逻辑与 range 范围查询合并
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

Java算法-力扣leetcode-167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 ****非递减顺序排列 ** ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < index2 < n…...

实战 | YOLOv10 自定义数据集训练实现车牌检测 (数据集+训练+预测 保姆级教程)
导读 本文主要介绍如何使用YOLOv10在自定义数据集训练实现车牌检测 (数据集训练预测 保姆级教程)。 YOLOv10简介 YOLOv10是清华大学研究人员在Ultralytics Python包的基础上,引入了一种新的实时目标检测方法,解决了YOLO以前版本在后处理和模型架构方面…...

自定义类型:结构体+结构体内存对齐+结构体实现位段
结构体内存对齐实现位段 一.结构体1.结构体的声明2.结构体变量成员访问操作符3.结构体传参4.匿名结构体5.结构的自引用 二.结构体内存对齐1.对齐规则2.为什么存在内存对齐?3.修改默认对齐数 三.结构体实现位段1.什么是位段2.位段的内存分配3.位段的跨平台问题4.位段…...
 command)
0109__strip(1) command
strip(1) command_linux strip-CSDN博客...

英码科技推出鸿蒙边缘计算盒子:提升国产化水平,增强AI应用效能,保障数据安全
当前,随着国产化替代趋势的加强,鸿蒙系统Harmony OS也日趋成熟和完善,各行各业都在积极拥抱鸿蒙;那么,边缘计算要加快实现全面国产化,基于鸿蒙系统开发AI应用势在必行。 关于鸿蒙系统及其优势 鸿蒙系统是华…...

从军事角度理解“战略与战术”
战略与战术,均源于军事术语。 战略(Strategy),源自希腊语词汇“strategos(将军)”和“strategia(军事指挥部,即将军的办公室和技能)”。指的是指挥全局性作战规划的谋略…...

最短路径——迪杰斯特拉与弗洛伊德算法
一.迪杰斯特拉算法 首先对于最短路径来说:从vi-vj的最短路径,不用非要经过所有的顶点,只需要找到路径最短的路径即可; 那么迪杰斯特拉的算法:其实也就与最小生成树的思想类似,找到较小的,然后…...
6.7.11 一种新的迁移学习方法可提高乳房 X 线摄影筛查中乳腺癌的诊断率
分割是一种将图像分割成离散区域的技术,以便将感兴趣的对象与周围环境分开。为了制定治疗计划,分割可以帮助医生测量乳房中的组织量。 二元分类问题的目的是将输入数据分为两组互斥的数据。在这种情况下,训练数据根据要解决的问题以二进制格…...
【Proteus8.16】Proteus8.16.SP3.exe的安装包,安装方法
下载: 链接:https://pan.baidu.com/s/14ZlETF7g4Owh8djLaHwBOw?pwd2bo3 提取码:2bo3 管理员打开proteus8.16.SP3.exe一路装就行了,许可证选Licence2.lxk,点安装后关闭,然后继续装完。 然后打开Patch-Proteus-8.16-…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
