基于小波多分辨分析的一维时间序列信号趋势检测与去除(MATLAB R2018a)
小波最开始是数学上提出的概念,并且在纯数学的王国里存在了一个世纪之久。最开始是为了弥补傅里叶分析的缺陷,即傅里叶级数发散的问题,并寻找出能够代替傅里叶分析的方法。从最早的一些艰难的探索开始直到慢慢发展成为一套完整系统的小波分析理论。早在1909年,Haar发现了最简单的小波,即Haar小波,到1982年Marr在计算视觉理论中提到的Marr小波,而后在1985年,Meyer提出了速降正则正交小波。1987年,Mallat提出小波多分辨率分析MRA用于正交小波的分解和重构。正是由于小波的多分辨分析特性,因此其具有“数学显微镜”的美称。再到后来小波作为信号分析和其他工程领域的分析工具开始流行起来,并在一些非线性问题中展现出强大的优势,人们渐渐看到了小波的无限魅力和潜力。正是由于小波分析理论完善的数学基础,以及小波优良的数值性能,各种类型的小波层出不穷,基于小波分析的一系列数值计算方法发展迅速。在实际应用中往往需要根据问题的特点及小波自身的特性选择或构造适合的小波基底构建形函数。
鉴于此,采用小波多分辨分析方法进行一维时间序列信号趋势检测与去除,运行环境为MATLAB R2018a,主运行代码如下,还是很容易理解的:
%% Load and visualize the signal
clc;clear
load ekgTrend.mat
helperTimeDomain(t,ekg_Trend,'EKG Signal',60,'r');
%% Decompose signal into 8 subbands
w = modwt(ekg_Trend,8);
%% Multiresolution view of signal
mra1 = modwtmra(w);
approxRecon = mra1(9,:);viewLevel8Approximation(t,ekg_Trend,approxRecon);
%% Visualize approximation subbands for level 9 and level 10
viewApproximationSubbandReconstruction(t,ekg_Trend);
%% Isolate and visualize the trend
isolateTrendPlot(t,ekg_Trend);
%% Remove the trend component from the signal
coeffs = modwt(ekg_Trend,10);
coeffs(11,:) = 0; %setting approximation coefficients at level 10 to zero
sigOut = imodwt(coeffs);
完整代码:https://mbd.pub/o/bread/mbd-Y52VlZxxviewDetrendedSignal(t,ekg_Trend,sigOut)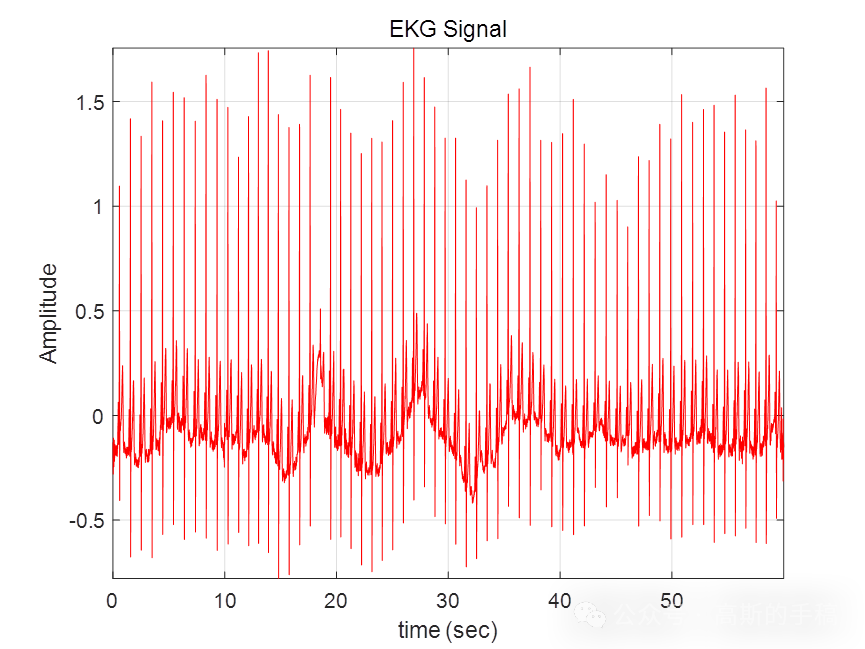




担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
相关文章:

基于小波多分辨分析的一维时间序列信号趋势检测与去除(MATLAB R2018a)
小波最开始是数学上提出的概念,并且在纯数学的王国里存在了一个世纪之久。最开始是为了弥补傅里叶分析的缺陷,即傅里叶级数发散的问题,并寻找出能够代替傅里叶分析的方法。从最早的一些艰难的探索开始直到慢慢发展成为一套完整系统的小波分析…...

Linux RedHat7.6操作系统的xfs格式化后,mount不生效
Linux RedHat7.6操作系统的xfs格式化后,mount不生效 问题现象 最近在准备测试环境的过程中,当对xfs文件系统格式化后,mount磁盘,通过df -h命令查看,未显示挂载磁盘信息 [rootZHZXLxjspo0db003 ~]# mount /dev/datavg/datavg-lv_data /data…...

高并发ping多台主机IP
简介 社区或者是大型公司往往有成千上万或者几百台设备,保持设备始终在线对网络运维人员来说至关重要,然而一个一个登录检查,或者一个一个ping并不明智,累人且效率极低,并出错率高。花钱买检测服务当我没说。 shell编…...

03 Linux 内核数据结构
Linux kernel 有四种重要的数据结构:链表、队列、映射、二叉树。普通驱动开发者只需要掌握链表和队列即可。 链表和队列 Linux 内核都有完整的实现,我们不需要深究其实现原理,只需要会使用 API 接口即可。 1、链表 链表是 Linux 内核中最简单、最普通的数据结构。链表是一…...

关于软件调用独显配置指引【笔记】
关于笔记本电脑不支持独显直连的,bios下也是没有切换独显直连的选项的,处理方法 简单的来说按照图片指引可配置让软件调用独显: 1、进入系统→屏幕→显示卡界面; 2、【添加应用】浏览需要调用独显的软件安装目录,并打开…...

正大国际期货:什么是主力合约?
一个期货品种,在同一时间段,会上市多个月份的合约, 由于主力合约交易量大,流动性高,一般建议新手交易主力合约。 主力合约通常指交易集中,流动性好的合约 ,即在一段时间内交易量和持仓量最大的…...

codeforces round 949 div2
A Turtle and Piggy Are Playing a Game 题目: 思路:输出2的幂次b使得2^b为最大的不超过x的数 代码: #include <iostream>using namespace std;const int N 2e5 10;void solve() {int l, r;cin >> l >> r;if(r % 2) …...

分享美好,高清无阻 - 直播极简联网解决方案
1、需求背景 随着移动互联网、UGC模式和直播平台的发展,网络直播的门槛日益降低,越来越多的人希望成为直播的主角。基于物联网的户外直播无线联网解决方案应运而生,满足直播者的需求。 户外直播无线联网解决方案提供了无处不在的直播体验&a…...

贪心算法-加油站
一、题目描述 二、解题思路 1.运动过程分析 这里需要一个油箱剩余油量的变量resGas,初始化resGas0;还需要一个标记从什么位置当做初始位置的startIdx,初始化startIdx0。 我们从数组下标idx0处开始向后遍历,初始时startIdx0&#…...
)
【ArcGIS微课1000例】0116:将度-分-秒值转换为十进制度值(字段计算器VBA)
相关阅读:【ArcGIS微课1000例】0087:经纬度格式转换(度分秒转度、度转度分秒) 文章目录 一、计算方法二、计算案例一、计算方法 将度分秒转换为十进制度的简单等式: DD = (Seconds/3600) + (Minutes/60) + Degrees如果角度值是负数,则转换方法不同。其中一种方法是: …...
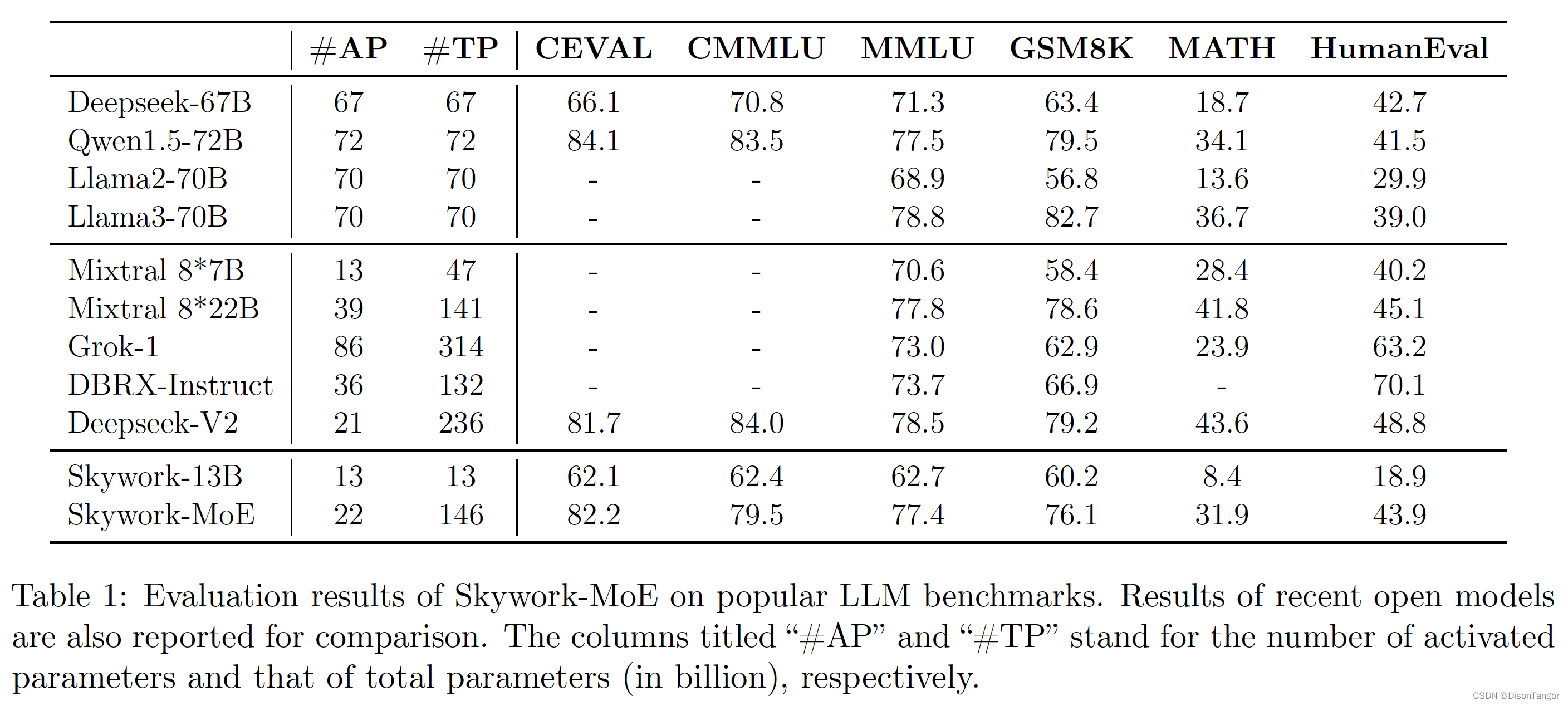
【中国开源生态再添一员】天工AI开源自家的Skywork
刚刚看到《AI高考作文出圈,网友票选天工AI居首》,没想到在Huggingface中发现了Skywork大模型。天工大模型由昆仑万维自研,是国内首个对标ChatGPT的双千亿级大语言模型,天工大模型通过自然语言与用户进行问答式交互,AI生…...
【机器学习300问】109、什么是岭回归模型?
在进行回归任务时间,可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高(几乎线性相关)时,标准的线性回归模型的系数估计可能非常不精确,可以理解成独立方程个数小于未知数个数此时方程有无穷多解。 例如&…...
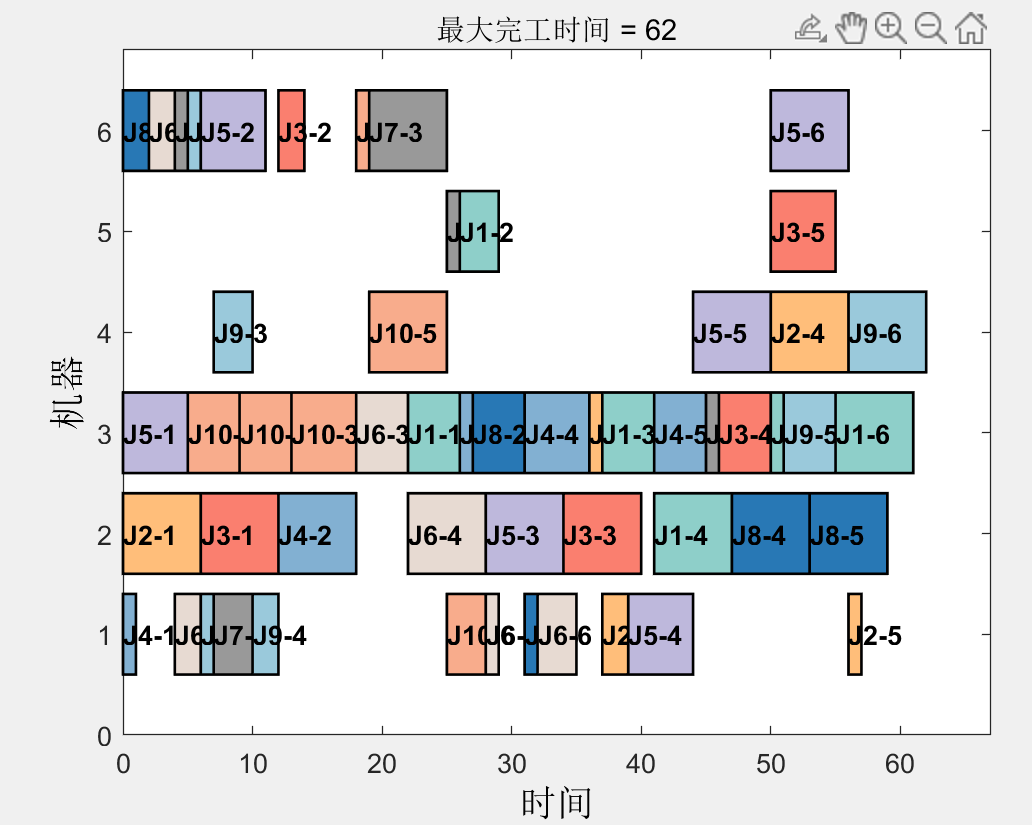
FJSP:烟花算法(FWA)求解柔性作业车间调度问题(FJSP),提供MATLAB代码
一、烟花算法介绍 参考文献: Tan, Y. and Y. Zhu. Fireworks Algorithm for Optimization. in Advances in Swarm Intelligence. 2010. Berlin, Heidelberg: Springer Berlin Heidelberg. 二、烟花算法求解FJSP 2.1FJSP模型介绍 柔性作业车间调度问题(Flexible …...

C++11 列表初始化(initializer_list),pair
1. {} 初始化 C98 中,允许使用 {} 对数组进行初始化。 int arr[3] { 0, 1, 2 };C11 扩大了 {} 初始化 的使用范围,使其可用于所有内置类型和自定义类型。 struct Date {int _year;int _month;int _day;Date(int year, int month, int day):_year(year…...
 和 endswith())
Python3 笔记:字符串的 startswith() 和 endswith()
1、startswith() 方法用于检查字符串是否是以指定子字符串开头,如果是则返回 True,否则返回 False。如果参数 beg 和 end 指定了值,则在指定范围内检查。 语法:str.startswith(substr, beg0,endlen(string)) 参数: s…...

Web前端安全问题分类综合以及XSS、CSRF、SQL注入、DoS/DDoS攻击、会话劫持、点击劫持等详解,增强生产安全意识
前端安全问题是指发生在浏览器、单页面应用、Web页面等前端环境中的各类安全隐患。Web前端作为与用户直接交互的界面,其安全性问题直接关系到用户体验和数据安全。近年来,随着前端技术的快速发展,Web前端安全问题也日益凸显。因此,…...
下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分)
1.单选题 (2分)下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分
1.单选题 (2分) 下列关于脚本的说法不正确的是( )。 A 线性脚本是最复杂的脚本 B 结构化脚本具有较好的可读性、可重用性,易于维护 C 关键字驱动脚本在开发时,不关心基础函数,直接使用已定义好的关键字 D 数据驱动脚本将测试脚本和数据进行分离,同一个脚本可以针对不同的输…...

【Docker系列】跨平台 Docker 镜像构建:深入理解`--platform`参数
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

力扣1248.统计优美子数组
力扣1248.统计优美子数组 同930. 哈希表法 求前缀和 class Solution {public:int numberOfSubarrays(vector<int>& nums, int k) {int n nums.size();unordered_map<int,int> cnt;int res0,sum0;for(int i0,j0;i<n;i){cnt[sum] ;if(nums[i] & 1) …...

AI2THOR 2.1.0使用教程
一、安装和入门 1.1 AI2-THOR使用要求 操作系统: Mac OS X 10.9, Ubuntu 14.04显卡:DX9(着色器型号 3.0)或 DX11,功能级别为 9.3。CPU:支持 SSE2 指令集。Python 2.7 或 Python 3.5Linux 用户…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
